Received 14 August 2015; accepted 8 September 2015; published 11 September 2015

ABSTRACT

The paper analyses time series that exhibit equilibrium states. It analyses the formation of equilibrium and how the system can return to the aforementioned equilibrium. The tool that is used in the aforementioned analysis is time optimal control in the phase plane. It is proved that equilibrium state is sustainable if initial state is not too far from the equilibrium as well as control vector is large enough. On the other hand, if initial state is one standard deviation away from equilibrium state, it is proved that equilibrium cannot be reached. It is the same case with control vector. If it is unbounded, time optimal control cannot be applied. The approach that is introduced re- presents unconventional method of analysing equilibrium in time series.

Keywords:

Time-Series, Equilibrium State, Time Optimal Control, Analysis, Control Vector, Financial Disruption

1. Introduction

Some physical systems exhibit equilibrium movement without intervention. Other physical systems exhibit disequilibrium movement but due to external factors, the equilibrium state is reached [1] . In mathematics, especially in differential equations, an equilibrium points is an optimal solution to a differential equation. Time optimal control is a method of mathematical optimisation for deriving control policies [1] .

Firstly, we will introduce the system of ordinary differential equations [2] :

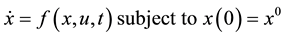(1)

The Equation (1) introduces the system of ordinary differential equations with an initial state. The 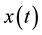is considered to be the state vector. The components 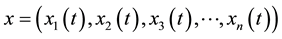are state variables while u is the control vector with control variables presented as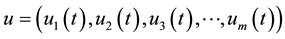. Firstly, u is merely integrable while f is continuously differentiable with respect to 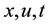so that we can allow for discontinuous changes in its components, the control variables.

2. Theoretical Results and Findings

A control problem that we pose is the following: if we take initial state as when t = 0 what control vector 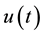can we choose that will take us to the target state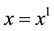, at time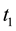. How can this system be controlled [2] ?

If the cost function is introduced

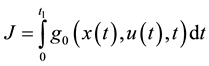(2)

and it is related to control problem, its minimisation by seeking controls u results with an optimal control problem. But we want to have time-optimal control problem. In order to obtain time-optimal control problem, we put 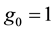and hence 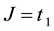so that we seek to minimize the time taken to reach the state. We will study this problem for the relatively simple first order differential linear, constant, coefficient equations:

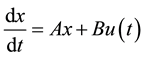(3)

We are going to study a time series graph, one line that is dependent of time and some other variable [3] . We assume that time series graph has an equilibrium position [3] , it is unstable and it can be moving in infinitely small time up and down. However, irrespectively of the other factors, we assume that time series graph has attained its equilibrium value. We want to find out what kind of external factor can affect it and make it move it out of equilibrium, as it is possible, that the time series graph tends to stay in equilibrium. In order to analyse the following problem, we use the following differential equation:

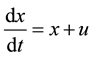(4)

where x represents the deviation from the equilibrium value, it could be called vertical deviation from the equilibrium as the 2D time series can move only up and down. As we assume that time series is in equilibrium, u represents external attempts that make the time series graph stays in equilibrium. If we assume that at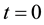, the deviation is existent and is presented like. Can this deviation be controlled and if it can be controlled, how quickly can it be controlled?

First case that we will analyse is that there is no attempt to control the deviation with, then the solution of equation is the following:

(5)

With no external factor affecting the time series graph, it is almost certain that the graph will move out of its equilibrium.

The equilibrium with is an unstable equilibrium point. In order to apply general control, we can solve (4) by using the integrating factor, so we have the following [4] :

(6)

And hence we have:

(7)

Since we want to have to analyse the system in equilibrium, we must have when, so we must have:

(8)

As, u must be negative for at least some period from. If is not bounded below, it is easy to choose u to satisfy, for example with, but however as we can only react in short time as stock price movement follows random walk and exchange rate is changing in infinitely small time intervals, we can control the system in an arbitrarily short time by making sufficiently large. At the same time, there are the systems in economy which control is unbounded, but then time-optimal problem is meaningless. We will take external factors to be in the range of.

In order to push x back towards the equilibrium as quickly as possible, we need to push as hard as possible by taking, so we get:

(9)

The solution is then

(10)

(11)

Equation (10) shows that as as. If then the system cannot be controlled back to equilibrium.

Figure 1 demonstrates that the equilibrium can only be achieved when deviation is less than one, then equilibrium can be reached. For the values that are higher than the equilibrium solution cannot be reached.

What is important to notice is that if x is above or below 1, the system is out of equilibrium, and as the time passes it diverges more from the equilibrium. We will introduce the controllable set which represents the set of initial states that can be controlled to the origin or equilibrium in some time. This is the union of all the controllable sets at time.

The controllable set is given as following [5] :

(12)

If C is the whole real line, , we say that the system is completely controllable. Since our system is not the whole real line, it means it is not completely controllable. Now, we must define the reachable set. It is the set where control exists.

From Equation (7), we have:

(13)

and since, we obtain:

(14)

so that we have:

(15)

defines the points in the reachable set. For, the reachable set doesn’t contain the origin and cannot reach the equilibrium. On the other side for, the origin or equilibrium is reachable for

.

In order to make the final assumption and summarise the analysis the following will be stated.

If time series graphs exhibit equilibrium state and tend to diverge from the aforementioned equilibrium state, external influence must be exerted via some of the external factors in order to attain equilibrium. This exertion of external influence can only be conducted in infinitely small time interval and must be sufficiently large. If the external influence or factor is unbounded, then optimal time control is not effective and this is what causes big financial disruptions or disruptions in any sense. It is also proved if equilibrium state of time series exhibit maximally one standard deviation, it can be returned to equilibrium state. Deviations larger than one standard deviation cause series to diverge from equilibrium level and to attain new equilibrium. At the same time, even if new financial equilibrium is established, there is still risk of financial disruption and crisis. Unfortunately, when we move away from time optimal control problem, we have to develop a new theory. At the same time, next step concerning the proposed theory is its testing and calibration.

3. Conclusion

This paper tries to introduce an innovative approach in time series analysis pertaining in that sense to time series that are characterized by equilibrium value. It introduces time optimal control problem and proves that the aforementioned time series can keep their equilibrium in case when the deviation is less than one standard deviation and under the condition that external influence is large enough. In case that external influence is too large, easily financial disruption can be caused. If the deviation from equilibrium is bigger than one s.d, it is possible that new equilibrium state is sought or the system doesn’t know how to behave and that there is a possibility of financial disruption until the state is stabilised again.

Acknowledgements

My sister Anna thanks a lot.

Cite this paper

OgnjenVukovic, (2015) Time Optimal Control in Time Series Movement. Journal of Applied Mathematics and Physics,03,1122-1125. doi: 10.4236/jamp.2015.39139

References