Journal of Applied Mathematics and Physics
Vol.03 No.06(2015), Article ID:57473,11 pages
10.4236/jamp.2015.36081
Improvement of Harmonic Balance Using Jacobian Elliptic Functions
Serge Bruno Yamgoué1, Bonaventure Nana1, Olivier Tiokeng Lekeufack2
1Department of Physics, Higher Teacher Training College-Bambili, The University of Bamenda, Bamenda, Cameroon
2Laboratory of Mechanics, Department of Physics, Faculty of Science, The University of Yaoundé 1, Yaoundé, Cameroon
Email: sergebruno@yahoo.fr, na1bo@yahoo.fr, lekeufackolivier@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 May 2015; accepted 22 June 2015; published 26 June 2015
ABSTRACT
We propose a method for finding approximate analytic solutions to autonomous single degree-of- freedom nonlinear oscillator equations. It consists of the harmonic balance with linearization in which Jacobian elliptic functions are used instead of circular trigonometric functions. We show that a simple change of independent variable followed by a careful choice of the form of anharmonic solution enable to obtain highly accurate approximate solutions. In particular our examples show that the proposed method is as easy to use as existing harmonic balance based methods and yet provides substantially greater accuracy.
Keywords:
Harmonic Balance, Linearization, Continuous Force Function, Single Degree-of-Freedom, Conservative System, Jacobian Elliptic Functions, Symmetric Oscillations

1. Introduction
Ordinary differential equations (ODEs in short) are ubiquitous in fundamental science as well as in engineering. Indeed they commonly arise as direct results of the application of some fundamental laws in the various fields of science or engineering. A classical example here is Newton’s second law of motion. They also often arise indirectly, for example, in the intermediate steps of solving other types of problems such as partial differential equations (PDEs). Solving ODEs, especially analytically, thus appears to be of great importance for gaining insights into real-world or engineering problems. This is yet a very challenging task since the ODEs of interest, being usually nonlinear, are rarely susceptible to exact analytical solutions. In fact, the lack of a general and systematic methodology for solving these nonlinear equations is probably the most important difficulty in the determination of their analytical solutions. So, for the important class of ODEs associated with oscillatory behaviors, numerous techniques which enable to obtain some approximations to the desired solutions have been developed. These techniques may be classified in two groups: perturbation and non-perturbation.
The most famous of perturbation approaches include the Lindstedt-Poincaré (LP) method, the method of multiple scales (MMS) and the Krylov-Bogoliubov-Mitropolsky (KBM) method. These now classical methods are known to have some serious limitations. For instance they are useless for equations which describe essentially nonlinear oscillators, such as (1) below with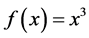 .
.
In contrast, non-perturbation techniques of which the method of harmonic balance (HB) is a well-known example, do not suffer these limitations. But the straightforward application of this last method leads to systems of nonlinear algebraic equations for the coefficients of the truncated Fourier series assumed for the solutions; which are still very difficult to solve. However the acuteness of this difficulty can now be reduced considerably thanks to the idea proposed initially by Wu and Li [1] and further refined by Wu and co-workers [2] [3] . It consists of linearizing the governing equations before applying the HB itself, which then leads to linear algebraic equations instead of nonlinear ones. The resulting method, harmonic balance with linearization (HBwL), has been applied to various types of conservative symmetric oscillators and appears to be both quite efficient and very simple [2] [3] , and references therein. Considering these two interesting properties, the method of HBwL is a good candidate for improvements which can make it to be more versatile than just conservative or symmetric systems. In this respect it has been adapted to handling dissipation terms in ODEs [4] , and more recently to solving asymmetric oscillator equations [5] .
Another important class of non-perturbative techniques involves the approximation of the nonlinear restoring force in a given oscillator ODE by some simple forms for which the exact solution can be readily obtained. The most common technique in this class is the method of equivalent linearization. In this approach the approximate ODE has the simple form of a linear harmonic oscillator equation [6] . Besides the method of equivalent linearization is the so-called method of “cubication” in which the restoring force function is expanded up to third order in Chebyshev polynomials. The method of cubiccation thus approximates a given ODE by a cubic Duffing equation whose exact solution is the approximate solution to the original ODE. It is well known that the exact solution of the Duffing equation can be expressed in explicit form using Jacobian elliptic functions [7] [8] .
In this paper, we investigate a further generalization of the HBwL by using Jacobian elliptic functions instead of circular trigonometric functions [7] . Our objective is to develop a higher order approximation than the single cnoidale elliptic function which is obtained when a given ODE is first approximated by a Duffing equation. We achieve this goal through a simple change of variable based on the properties of the Jacobian elliptic functions, which results to an ODE in which the restoring force is not approximated and which is solved approximately following the method of HBwL or other generalizations of the method of HB such as the rational HB.
The paper is organized as follows. The main idea sustaining the elliptic harmonic balance is introduced in the next section. The illustrations are presented next in Section 3, where examples of oscillators with polynomial and rational restoring force functions are considered. Section 4 contains the conclusion of the paper.
2. Presentation of the Approach
We consider a nonlinear second-order differential equation of the general form
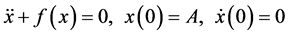 (1)
(1)
which governs the time (t) evolution of the state of the state (x) of a conservative single degree-of-freedom system. Here, an overdot denotes differentiation with respect to time t. Thus, 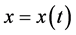 is a real function. We assume without loss of generality that
is a real function. We assume without loss of generality that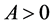 . The restoring force function f is a general nonlinear function of x which is required to be continuous and to satisfy
. The restoring force function f is a general nonlinear function of x which is required to be continuous and to satisfy 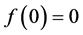 and
and 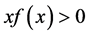 for
for 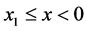 and
and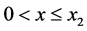 ; where x1 and x2 are two constants. For simplicity we shall restrict ourselves in this paper to the case where f is additionally odd,
; where x1 and x2 are two constants. For simplicity we shall restrict ourselves in this paper to the case where f is additionally odd,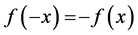 ; so that the system oscillates symmetrically around
; so that the system oscillates symmetrically around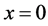 . Our objective is to determine an approximate analytic solution to the periodic solution of the above equation. It is customary in classical techniques [3] [9] - [12] to introduce a time scaling according to
. Our objective is to determine an approximate analytic solution to the periodic solution of the above equation. It is customary in classical techniques [3] [9] - [12] to introduce a time scaling according to
 (2)
(2)
Here, T and w are the unknown time-period and angular frequency of the sought periodic solution. Under this scaling, (1) becomes
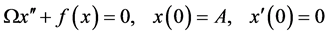 (3)
(3)
where we have set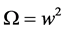 , and a prime denotes a differentiation with respect to τ. The periodic solutions of this latter equation are 2π-periodic in τ.
, and a prime denotes a differentiation with respect to τ. The periodic solutions of this latter equation are 2π-periodic in τ.
In this paper we use a different time-scaling than (2) which is simply linear in τ. Following Yuste Bravo [7] , we consider the generally nonlinear transformation given by
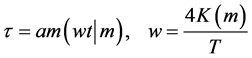 (4)
(4)
where am is the Jacobian elliptic amplitude function of parameter m while K is the complete elliptic integral of the first kind. In this paper we adopt the notation of [13] for designating elliptic functions. The parameter m is an additional unknown to be determined as part of the solution. It should be noted that (2) is a particular case of (4), corresponding to the fixed value m = 0. Using the following well-known property of the am function
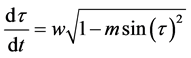 (5)
(5)
one can easily show that the nonlinear time-scaling (4) transforms (1) into
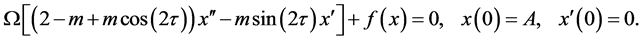 (6)
(6)
Notice that (6) reduces to (3) for m = 0. The former differs from the latter only by two terms which are parametrically linear in the derivatives. Thus if the HB can be applied to the latter, which requires that one be able to compute the Fourier series of 





Then, by making the substitutions 





and



are applicable respectively for m < 0 and m > 1. Thus the results that would be obtained using the proposed approach are valid for all real values of such that 



in which 


3. Illustrations
Two examples are now presented for illustration.
3.1. The Cubic-Quintic Duffing Oscillator
Our first example involve the cubic-quintic Duffing oscillator described by (1) with f defined such that

Since



Substituting this in (6) with the above form of f and equating the coefficients of 



The solution of this set of equations is found to be (recall that


The explicit solution associated with (12) is as in (18a) below. Some limiting cases can be verified readily: For






The results obtained at this level are exactly the same that would be obtained by cubication [16] . In effect, the third order Chebyshev expansion of (11) in the range of interest, 

where 


The method of cubication therefore approximates (1) with (11) by

with

The solution of (17a) can be written explicitly as [16]

with

One can easily verify that for μ and λ defined by (17b) the expressions of and in (18b) and (14) are the same. This shows that the method of cubication and the lowest order harmonic balance in our proposed approach are equivalent. But unlike the method of cubication whose results would be limited to the above, the transformation proposed herein allows for further improvments. For instance, the approximate solution to (6) can be sought directly in the form

The required Fourier series expansion is quite easily calculated for polynomial restoring force functions. By equating the coefficients of





we can express w and m as follows


where d solves the polynomial equation

The coefficients of the above polynomial equations are as follows:

Since

Using (7a) for 


It appears obviously from (23) that 




It deserves to point out here that one could have considered the improved solution in the form

as was suggested by Yuste Bravo [7] . The expression of b following the linearization procedure is found in this case to be

As can be seen, this expression is independent of the coefficient of the linear term α in contrast to (23). The consequence of this is that (25) is less versatile than (19) to accurately approximate the solutions of the Duffing oscillator for all combinations of the coefficients of its terms. In effect, we have noticed that (25) is very poor when 

To further appreciate the accuracy of the various approximations obtained above, we use the relative error

to compare the approximate period

to the exact period
Figure 1. Comaprison of the approximate solutions to the exact solution for the cubic- quintic Duffing oscillator for 


Consider first the case 


Calculations using the approximate expressions derived above show that the relative errors of the first-order and second-order analytical approximations as compared to the exact solution are respectively less than 0.37% and 0.072%. In comparison it would be necessary to proceed up to the third-order approximation of the standard HBwL to obtain a result just better than our least accurate first-order result; with a relative error of 0.23% [17] .
In Figure 2 we compare the relative errors of the single harmonic approximation or cubication, the standard HBwL, and the anharmonic solution when


A further comparison is presented in Figure 3 for situations where heteroclinic orbits connecting two distinct equilibrium points exist. Once again we observe that our approach generally provides the best accurate approximation. We should point out however that as the oscillation amplitude approaches critically the value for which heteroclinic trajectory is realized, the accuracy of the standard HBwL supersedes our result.
3.2. An Oscillator with Rational Restoring Force
As a second example, we consider a conservative nonlinear oscillatory system in which the restoring force has a rational form. Specifically we choose

A peculiarity of this function which is worth noting is that it is not dominated by odd-power monomials in both of the limiting cases 



Figure 2. Comparison of the relative errors for the cubic-quintic Duffing oscillator for
Figure 3. Comparison of the relative errors for the cubic-quintic Duffing oscillator for 
For this form of the restoring force function the expressions of μ and λ in the cubic Duffing equation (17a) approximating (1) with (31) are given by


It follows that the expressions of the parameters m and w of the approximate solution of the problem using the method of cubication are

Again these expressions can also be obtained through the lowest order harmonic balance method for (6) with (31). They solve exactly the coefficients of the fundamental and third order harmonics in the residual of this equation when







and

with

To appreciate the accuracy of the two approximate results in (33) and (34) we have plotted in Figure 4 the corresponding period calculated as 

as a function of A. It appears clearly from this figure that the result obtained from the method of cubication so diverges from the exact result for large oscillation amplitudes that it can simply be considered invalid. However a good match is observed between the result of our proposed approach and the exact result. Figure 5 indicates that the maximum relative error on the period is achieved for 
4. Conclusion and Remarks
In this paper we have investigated the approximation of periodic solutions to autonomous single degree-of- freedom oscillators equations using the Jacobian elliptic function with the objective of improving the method of cubication. To this end we have shown that the properties of these functions can be exploited to put such ODEs
Figure 4. Comparison of harmonic (magenta triangle), anharmonic (blue circle) and numerical (black star) period for the rational restoring force oscillator.
Figure 5. Relative percentage error on the period for the rational restoring force oscillator.
in a form for which the standard HB and like methods can be applied, while the result is however expressed in terms of Jacobian elliptic functions. Our investigation reveals that in the HBwL the harmonics to include in the correction to a given stage should be higher than or equal to the least harmonic of the residual terms of that stage. With the change of variable sustaining our approach, the analysis can be carried out to higher order, just as in the standard HBwL. For our examples, comparison to the standard harmonic balance indicates that our approach is generally the best, except for periodic orbits too close to a heteroclinic orbit. However, even in this case, the standard HBwL has to be carried to higher order than our approach to gain this advantage. Such a higher order analysis can be quite intricate for non polynomial restoring force. A further interesting property of the solution resulting from our approach is that it also approximates all the harmonics of the exact solution. While the method of rational harmonic balance and the method of cubication also offer solutions with this property, they do not include a mean to carrying the approximations to higher orders as in the present work. In fact our method encompasses the method of cubication which is equivalent to ist first order application.
Cite this paper
Serge Bruno Yamgoué,Bonaventure Nana,Olivier Tiokeng Lekeufack, (2015) Improvement of Harmonic Balance Using Jacobian Elliptic Functions. Journal of Applied Mathematics and Physics,03,680-690. doi: 10.4236/jamp.2015.36081
References
- 1. Wu, B.S. and Li, P.S. (2001) A Method for Obtaining Approximate Analytical Periods for a Class of Nonlinear Oscillators. Meccanica, 36, 167-176. http://dx.doi.org/10.1023/A:1013067311749
- 2. Wu, B.S. and Lim, C.W. (2004) Large Amplitude Non-Linear Oscillations of a General Conservative System. International Journal of Non-Linear Mechanics, 39, 859-870.
http://dx.doi.org/10.1016/S0020-7462(03)00071-4 - 3. Wu, B.S., Sun, W.P. and Lim, C.W. (2006) An Analytical Technique for a Class of Strongly Non-Linear Oscillators. International Journal of Non-Linear Mechanics, 41, 766-774.
http://dx.doi.org/10.1016/j.ijnonlinmec.2006.01.006 - 4. Yamgoué, S.B. and Kofané, T.C. (2008) Linearized Harmonic Balance Based Derivation of the Slow Flow for Some Class of Autonomous Single Degree of Freedom Oscillators. International Journal of Non-Linear Mechanics, 43, 993- 999. http://dx.doi.org/10.1016/j.ijnonlinmec.2008.05.001
- 5. Yamgoué, S.B. (2012) On the Harmonic Balance with Linearization for Asymmetric Single Degree of Freedom Non-Linear Oscillators. Nonlinear Dynamics, 69, 1051-1062.
http://dx.doi.org/10.1007/s11071-012-0326-1 - 6. Nayfeh, A.H. and Mook, D.T. (1979) Nonlinear Oscillations. Wiley, New York
- 7. Yuste Bravo, S. (1991) Comments on the Method of Harmonic Balance in Which Jacobian Elliptic Functions Are Used. Journal of Sound and Vibration, 145, 381-390.
http://dx.doi.org/10.1016/0022-460X(91)90109-W - 8. Yuste Bravo, S. (1992) “Cubication” of Non-Linear Oscillators Using the Principle of Harmonic Balance. International Journal of Non-Linear Mechanics, 27, 347-356. http://dx.doi.org/10.1016/0020-7462(92)90004-Q
- 9. Nayfeh, A.H. (1973) Perturbation Method. Wiley, New York.
- 10. Amore, P. and Aranda A. (2003) Presenting a New Method for the Solution of Nonlinear Problems. Physics Letters A, 316, 218-225. http://dx.doi.org/10.1016/j.physleta.2003.08.001
- 11. Pelster, A., Kleiner, H. and Schanz, M. (2003) High-Order Calculation for the Frequency of Time-Periodic Solutions. Physical Review E, 67, Article ID: 016604.
http://dx.doi.org/10.1103/PhysRevE.67.016604 - 12. Yamgoué, S.B., Bogning, J.R., Kenfack Jiotsa, A. and Kofané, T.C. (2010) Rational Harmonic Balance-Based Approximate Solutions to Nonlinear Single-Degree-of-Freedom Oscillator Equations. Physica Scripta, 81, Article ID: 035003. http://dx.doi.org/10.1088/0031-8949/81/03/035003
- 13. Abramowitz, M. and Stegun, I.A. (1972) Handbook of Mathematical Functions. Dover, New York.
- 14. Gradshteyn, I.S. and Ryzhik, I.M. (2000) Table of Integrals, Series, and Products. 6th Edition, Academic Press, San Diego.
- 15. Mickens, R.E. (2002) Fourier Representations for Periodic Solutions of Odd-Parity Systems. Journal of Sound and Vibration, 258, 398-401. http://dx.doi.org/10.1006/jsvi.2002.5200
- 16. Beléndez, A., Méndez, D.I., Fernandez, E., Marini, S. and Pascual, I. (2009) An Approximate Solution to the Duffing-Harmonic Oscillator by a Cubication Method. Physics Letters A, 373, 2805-2809. http://dx.doi.org/10.1016/j.physleta.2009.05.074
- 17. Lai, S.K., Lim, C.W., Wu, B.S., Wang, C., Zeng, Q.C. and He, X.F. (2009) Newton-Harmonic Balancing Approach for Accurate Solutions to Nonlinear Cubic-Quintic Doffing Oscillators. Applied Mathematical Modelling, 33, 852-866. http://dx.doi.org/10.1016/j.apm.2007.12.012






