Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56537,5 pages
10.4236/jamp.2015.35064
A New Method of Measurement of the True Temperature and Emissivity of Non-Black Body Using One Component of Wien’s Spectrum of Thermal Radiation
D. Ya. Svet
Joint Institute for High Temperatures of the Russian Academy of Sciences, Moscow, Russian Federation
Email: vsvetd@mail.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 March 2015; accepted 20 May 2015; published 22 May 2015
ABSTRACT
It is shown that the measurement of only one component of the Wein’s spectrum of thermal radia- tion in range λT ≤ 3000 (˚C μm) is sufficient to estimate the true temperature and spectral emissivity of the selected component with sufficient accuracy, although more than one hundred years this statement was considered as incorrect. The proposed method is based on the formation of the linear dependence of the logarithm of the emissivity of not real wavelengths and artificially gen- erated “virtual” spectral components.
Keywords:
True Temperature, Spectral Emissivity, Wein’s Law

1. Introduction
Since the discovery of Wien’s exponential law of thermal radiation the concepts of emissivity and black-body factor were firmly established in physics. And measuring of the true temperature and emissivity became a problem “idem per idem” (the same through the same): To measure the true temperature it is necessary to know the emissivity and vice versa. A close look at this problem (on which the author spent more than sixty years) showed that its solution exists. Moreover, it was found that the measurement of any of the spectral components of radiation following to an exponential Wien’s law is enough to determine the value of true temperature and spectral emissivity of this component. Below we shall describe the proposed method which implements this statement1.
2. Method
The method is based on the principle of double spectral ratio, based on the linear dependence of the logarithm of the emissivity for three selected components of the spectrum of thermal radiation, proposed in [1] [2] , which is widely represented in the literature [3] . However, application of this principle is limited by the requirement on the linearity a priory. This takes place practically only for wavelengths with very closed spacing, which in turn leads to increasing of the value of equivalent wavelength, i.e. to an unacceptable increasing error of measured temperature.
In proposed method a linear dependence of the three components, two of which are “virtual”, is generated artificially relative the selected spectral component and the requirement of proximity of wavelengths is eliminated.
Thus, only one spectral component is extracted from the Wien’s spectrum that is logarithmic,
 (1)
(1)
where:
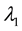 ―wavelength;
―wavelength;
 ―temperature in ˚C;
―temperature in ˚C;
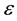 ―spectral emissivity at wavelength λ1;
―spectral emissivity at wavelength λ1;
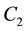 ―14,388 μm/˚C―second pyrometer constant.
―14,388 μm/˚C―second pyrometer constant.
The value of the second pyrometer signal is determining by multiplying  on the ratio
on the ratio  which is proportional to a “virtual” spectral component at a selected wavelength
which is proportional to a “virtual” spectral component at a selected wavelength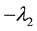 , more or less than
, more or less than . For exam- ple, let’s choose
. For exam- ple, let’s choose 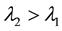
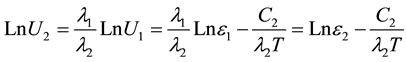 (2)
(2)
where 
Further, let’s form a third pyrometer signal proportional to the “virtual” component with a wavelength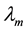 , which, for example, defined by the half-sum of inverse values of wavelengths
, which, for example, defined by the half-sum of inverse values of wavelengths
 , i.e.
, i.e.
 (3)
(3)
where
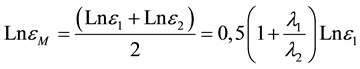 (4)
(4)
Thus

Having these three pyrometer signals


Graphically this is shown in Figure 1, where the emissivity’s of these three signals marked by ordinates


Figure 1. Emissivity versus wavelength.
length.
For the linearization of this dependence and formation of a linear dependence (this is a straight line 
This formula determines the value of the true temperature at known a’priory linearity of logarithm of emis- sivity from the wavelength and has the form:

where 


Usually for method of double spectral ratio the relation 
Thus, substituting the values of



And get the expression for the “resultant” emissivity in the form of

If to follow to the linear dependence of emissivity from wavelength the “resultant” emissivity must be equal to zero,

This can be seen from the formula (7) for V and illustrated in Figure 1, where: 


Let’s change the value of



Thus, we determine the value of

Substituting the expression for 


where 
Thus, the expression (6) for V, specifying the desired value of the true temperature at a linear dependence of the logarithm of the emissivity will have the form:

or 
Moreover,
Thus, the desired value of the true temperature will be equal to

where,
And the emissivity will be equal to

3. Example
As an example of proposed method let’s present the result of calculation of the true temperature for steel; data are taken from [5] . This work contains the following data:
Steel



Let’s now choose a second “virtual” wavelength from the spectrum of thermal radiation, for example,

Then

The third signal 
where:

To provide the linearity of logarithm of emissivity let’s change the value
Now by substituting 



where:
Therefore 

or
Therefore, the required temperature will be equal to
And the resulting error will be
The value of the logarithm of the emissivity will be equal to

And the resulting error will be


From this example we can see that proposed method based on selection of “virtual” components provides rather good accuracy.
Note that if to select the second “virtual” component of the spectrum with a wavelength




4. Conclusion
The described method and calculations performed on its base show that it can estimate fairly accurately the value of the true temperature and emissivity using only one real spectral component and two complementary “virtual” components of the emissivity spectrum which follows to Wien’s law and additional virtual spectral components can be selected rather arbitrarily. From a mathematical point of view, the proposed method is not rigorous, because formally Equation (1) includes two unknown parameters and the proposed heuristic approach is rather geometric in nature, but it provides, and quite simply, accurate measurements of true temperature and emissivity in spectral region
Acknowledgements
I am grateful to the staff of the Academic Council of the Joint Institute for High Temperatures of the Russian Academy of Sciences for fruitful discussion of this work.
References
- Svet, D.Ya. (1975) Color Pyrometer of True Temperature. Certificate of Invention, No. 476464. Bulletin of Inventions, Moscow.
- Svet, D.Ya. (1982) Optical Methods for Measuring the True Temperature. Nauka, Moscow, 145.
- Hornbeck, G.A. (1962) Temperature: Its Measurement and Control in Science and Industry. Reinhold V.I., New-York, 262.
- Svet, D.Ya. (1985) 3-Wavelength Radiation Pyrometer. Certificate of Invention No. 1284336. Bulletin of Inventions, Moscow.
- Shvarev, K.M., Gushchin, V.S., Baum, B.A. and Held, V.P. (1979) Optical Constants of Iron-Carbon Alloys in the Temperature Range 20˚C - 1600˚C. Teplofizika, 17, 66-71.
NOTES
1Patent is pending, D. Ya. Svet, patent application No. 2014143378 from 28.10.2014.















