Journal of Applied Mathematics and Physics Vol.02 No.13(2014),
Article ID:52516,5 pages
10.4236/jamp.2014.213139
Spin Glass Phase Exists in the Random Weak Disorder for the Villain Model
Md. Yeakub Ali*, Sunil Dhar
Department of Mathematics, Chittagong University of Engineering and Technology, Chittagong, Bangladesh
Email: *ali69cuet@gmail.com, sdhar@cuet.ac.bd
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 August 2014; revised 19 September 2014; accepted 7 October 2014
ABSTRACT
In this work we have studied non random Villain model by introducing simple defects
to calculate degeneracies of the first excited states using Pfaffian approach through
a perturbation theory. The distributions of excitations of the ground states are
displayed graphically. The results are indicated that spin glass occurs in the weak
disorder for the Villain model. At the concentration of defect bonds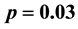 ,
the distribution behaves in the same manner as for
,
the distribution behaves in the same manner as for
 for different sizes of lattice. The latest result of the spin glass is presented
in this paper.
for different sizes of lattice. The latest result of the spin glass is presented
in this paper.
Keywords:
Spin Glass, First Excitations, Distribution, Square Lattice

1. Introduction
In this paper we have presented computational results for excitations of ground states for the Villain model [1] by introducing simple defects. In the Villain model, we have replaced ferromagnetic bonds by antiferromagnetic bonds randomly and calculated first excitations in the concentrations of defect bonds p = 0.01 to 0.5 for the whole random system. The initial model is fully frustrated [2] with highly degeneration of ground states and the replacement of ferromagnetic bonds with antiferromagnetic bonds reduces frustration [3] . The spin glasses are disorder system [3] which is defined as the random combinations of ferromagnetic and antiferromagnetic bonds.
We have expected the Villain model to have a spin glass at zero temperature in the
aforementioned limit of weak disorder. In this study, the square lattice
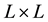 is wounded cylindrically and the periodic boundary condition is in one dimension.
The energy gap is 4J in the mentioned system if L is even. Otherwise it is 2J [4]
[5] . In this work, we propose a simple picture of spin glass phase in the weak
disorder that has evaluated from power law distribution of first excitations of
ground states.
is wounded cylindrically and the periodic boundary condition is in one dimension.
The energy gap is 4J in the mentioned system if L is even. Otherwise it is 2J [4]
[5] . In this work, we propose a simple picture of spin glass phase in the weak
disorder that has evaluated from power law distribution of first excitations of
ground states.
An outline of this paper is as follows. In Section 2 we introduce formalism and discuss with model and method how one can calculate first excitations. In Section 3 we present results from numerical simulation of the Villain model with antiferromagnetic exchange randomness and in Section 4 we draw concluding remarks.
2. Formalism
The frustration of two dimensional Ising model with interaction in one dimension
is studied in this paper extensively. The two dimensional fully frustrated Ising
model, or Villain model [1] , consists of Ising spins on a square lattice with nearest
neighbor bonds
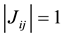 with periodic boundary conditions. The Hamiltonian can be written as
with periodic boundary conditions. The Hamiltonian can be written as
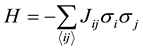 (1)
(1)
where
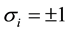 are Ising spins on a square lattice,
are Ising spins on a square lattice,
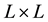 as shown in
Figure 1.
as shown in
Figure 1.
The method is used in the calculation basing on the Pfaffian [5] through a degenerate state perturbation theory [6] - [8] . The degeneracies of the excitated states are calculated from an expression of the eigenvalues with disorder subspace. We write the partition function for the two dimensional Ising model as
 (2)
(2)
where
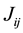 is the nearest-neighbour bond strength for sites
is the nearest-neighbour bond strength for sites
 and the product is over all bonds on the N-site lattice. The Matrix D [9] - [15]
is Hermitian, pure imaginary, and of order 4N. The eigenvalue of Matrix D can be
written
and the product is over all bonds on the N-site lattice. The Matrix D [9] - [15]
is Hermitian, pure imaginary, and of order 4N. The eigenvalue of Matrix D can be
written
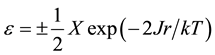 (3)
(3)
where r is an integer and X is a real number. At T = 0 there is a degeneracy at
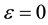 equal to the number of frustrated plaquettes. The expression the ground-state degeneracy
are written a
equal to the number of frustrated plaquettes. The expression the ground-state degeneracy
are written a
 (4)
(4)
where
 is the degeneracy of the ith excitated states. The entropy of the bimodal spin glass
Ising model can be expressed in terms of the degeneracies as
is the degeneracy of the ith excitated states. The entropy of the bimodal spin glass
Ising model can be expressed in terms of the degeneracies as
 (5)
(5)
The specific heat of the system can be written as
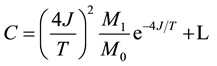 (6)
(6)
Figure 1. The Villain model
on

3. Results and Discussion
We have carried out a numerical calculation to lift degeneracies of excited states
at zero temperature. The disorder is confined to a frustrated square patch with
periodic boundary conditions in one dimension. Square lattices of size



are the most likely value in the scale



Figure 2. At concentration
of defect bonds


Figure 3. At concentration
of defect bonds


Figure 4. At concentration
of defect bonds


Figure 5. At concentration
of defect bonds


Figure 6. At concentration
of defect bonds




Figure 7. At concentration
of defect bonds



4. Conclusion
We have carried out a numerical study of the Villain model, showing that there is
an observation that indicates a zero temperature spin glass phase with weak disorder.
We have used a computer code that is able to collect numerical data for simulation.
The Pfaffian approach is used to collect data for first excitations of ground states,
based on perturbation theory. It has been observed clearly that the spin glass phase
occurs at concentration of defect bonds
Acknowledgements
The authors are grateful to the authority of Chittagong University of Engineering and Technology (CUET). The authors also would like to thanks Professor Dr. Julian Poulter for valuable advise during the research work.
References
- Villain, J. (1977) Spin Glass with Non-Random Interactions. Journal of Physics C: Solid State Physics, 10, 1717. http://dx.doi.org/10.1088/0022-3719/10/10/014
- Ali, M.Y. and Poulter, J. (2013) Spin Correlation Function of the Fully Frustrated Ising Model and ±J Ising Spin Glass on the Square Lattice. Chinese Physics B, 22, Article ID: 067502. http://dx.doi.org/10.1088/1674-1056/22/6/067202
- Mezard, M., et al. (1987) Spin Glass Theory and Beyond. World Scientific, Singapore.
- Atisattapong, W. and Poulter, J. (2008) Energy Gap of the Bimodal Two-Dimensional Ising Spin Glass. New Journal of Physics, 10, Article ID: 093012. http://dx.doi.org/10.1088/1367-2630/10/9/093012
- Jinuntuya, N. and Poulter, J. (2012) Elementary Excitations and the Phase Transition in the Bimodal Ising Spin Glass Model. Journal of Statistical Mechanics: Theory and Experiment, 2012, Article ID: P01010. http://dx.doi.org/10.1088/1742-5468/2012/01/P01010
- Blackman, J.A. and Poulter, J. (1991) Gauge-Invariant Method for the ±J Spin-Glass Model. Physical Review B, 44, 4374. http://dx.doi.org/10.1103/PhysRevB.44.4374
- Katzgraber, H.G., et al. (2007) Effective Critical Behavior of the Two Dimensional Ising Spin Glass with Bimodal Interaction. Physical Review B, 75, Article ID: 014412.
- Kac, M. and Ward, J.C. (1952) A Combinatorial Solution of the Two Dimensional Ising Model. Physical Review, 88, 1332. http://dx.doi.org/10.1103/PhysRev.88.1332
- Green, H.S. and Hurst, C.A. (1964) Order-Disorder Phenomena. In-Terscience, London.
- Blackman, J.A. and Poulter, J. (1982) Two-Dimensional Frustrated Ising Network as an Eigenvalue Problem. Physical Review B, 26, 4987. http://dx.doi.org/10.1103/PhysRevB.26.4987
- Wang, J.S. and Swendens, R.H. (1988) Monte Carlo Renormalization Group Study of Ising Spin Glasses. Physical Review B, 38, 4840. http://dx.doi.org/10.1103/PhysRevB.37.7745
- Fischer, K.S. and Hertz, J.A. (1991) Spin Glasses. Cambridge University Press, London. http://dx.doi.org/10.1017/CBO9780511628771
- Stein, D. (1992) Spin Glasses and Biology. World Scientific, Singapore. http://dx.doi.org/10.1142/0446
- Sherrington, D. Spin Glasses. Preprint: cond-mat/9806289
- Pathria, R.K. (1972) Statistical Mechanics. Pergamon Press, New York.
NOTES
*Corresponding author.











