Journal of Applied Mathematics and Physics
Vol.2 No.8(2014), Article
ID:47817,8
pages
DOI:10.4236/jamp.2014.28087
A Mixed Convection Boundary Layer Flow over a Vertical Wall in a Porous Medium, with Exponentially Varying Fluid Viscosity
Eunice Mureithi
Department of Mathematics, University of Dar es Salaam, Dar es Salaam, Tanzania
Email: ewambui02@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2014; revised 18 June 2014; accepted 3 July 2014
ABSTRACT
This study investigates a mixed convection boundary layer flow over a vertical wall embedded in a highly porous medium. The fluid viscosity is assumed to decrease exponentially with temperature. The boundary layer equations are transformed into a non-similar form using an appropriate nonsimilar variable  and a pseudo-similar variable
and a pseudo-similar variable![]() . The non-similar equations are solved using an efficient local non-similarity method. The effect of viscosity variation parameter on the heat transfer, skin friction and the velocity and temperature distribution within the boundary layer is investigated. The viscosity variation parameter, the viscous dissipation parameter and non-similarity variable are shown to have a significant effect on velocity and thermal boundary layer and also on the skin friction coefficient and heat transfer at the wall.
. The non-similar equations are solved using an efficient local non-similarity method. The effect of viscosity variation parameter on the heat transfer, skin friction and the velocity and temperature distribution within the boundary layer is investigated. The viscosity variation parameter, the viscous dissipation parameter and non-similarity variable are shown to have a significant effect on velocity and thermal boundary layer and also on the skin friction coefficient and heat transfer at the wall.
Keywords:Porous Medium, Non-Darcy, Mixed Convection Boundary Layer, Temperature Dependent Viscosity

1. Introduction
Mixed convection boundary layer flow through a porous medium is of primary importance due to its applications in industry such as geothermal operations (for example dynamics of hot springs), terrestrial heat flow through an aquifer, flow of moisture through porous industrial material etc. Engineering applications include porous thermal insulation and heat exchangers with fluidized beds etc.
Reviews on convective heat transfer in porous medium are well documented in the books by Nield and Bejan, [1] and Pop and Ingham [2] , Kaviany [3] and in the handbook of porous media edited by Vafai [4] . Numerous studies on mixed convection boundary through a porous media using the Darcy model and extended Darcy models have been carried out, by others, by Karabis et al. [5] investigated a mixed forced-free convection boundary layer flow over a vertical wall in a highly porous medium, Chen [6] who looked at a boundary layer flow over a horizontal in a saturated porous medium. Using the model developed by Vafai and Tien [7] , Hong et al. [8] investigated the non-Darcian effects on a flow over a vertical plate in porous media.
Most fluids used in engineering have temperature varying viscosity. A study by Hossain and Munir [9] investigated a mixed convection boundary layer with temperature dependent viscosity where it was shown that the viscosity variation parameter has an effect on the wall skin friction coefficient and wall heat transfer coefficient. Jayanthi and Kumari [10] studied the effects of variable viscosity on a non-Darcy flow of a non-Newtonian fluid over a vertical surface in porous medium. They showed that variable viscosity parameter has a significant effect on the fluid flow properties.
The current study focuses on a boundary layer flow over a vertical wall embedded in a highly porous medium and with variable viscosity. The non-similar boundary layer equations are solved using the local non-similarity method due to Sparrow et al. [11] and Sparrow and Yu [12] . In Section 2 the mixed convection boundary layer flow equations are formulated and transformed to the non-similar form, in Section 3 the equations are solved and the results presented and discussed in Section 4. Conclusions are drawn in Section 5.
2. Mixed Convection Boundary Layer Flow in a Porous Medium
A steady, two-dimensional flow of a viscous incompressible fluid over a heated semi-infinite vertical wall embedded in a highly porous medium is studied. The ![]() -axis is taken along the wall and the
-axis is taken along the wall and the 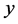 -axis as the normal axis to
-axis as the normal axis to ![]() -axis. The free-stream velocity and temperature are taken as
-axis. The free-stream velocity and temperature are taken as 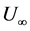 and
and ![]() respectively and the wall temperature as
respectively and the wall temperature as . The fluid viscosity
. The fluid viscosity 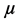 is assumed to decrease exponentially with temperature. Under the boundary layer approximation for a flow through a porous medium and the Boussinesq's approximation, the mixed convection boundary layer equations through a porous media take the form:
is assumed to decrease exponentially with temperature. Under the boundary layer approximation for a flow through a porous medium and the Boussinesq's approximation, the mixed convection boundary layer equations through a porous media take the form:
 (2.1)
(2.1)
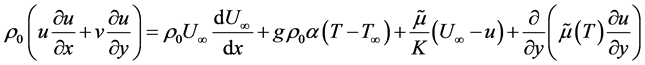 (2.2)
(2.2)
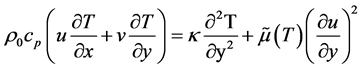 (2.3)
(2.3)
The appropriate boundary conditions for the flow are:
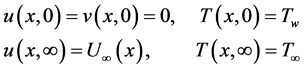
Here 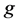 is the gravitational acceleration,
is the gravitational acceleration, 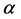 is the coefficient of thermal expansion,
is the coefficient of thermal expansion, ![]() is the thermal conductivity,
is the thermal conductivity, 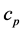 is the specific heat at constant pressure,
is the specific heat at constant pressure, ![]() is the fluid density at reference temperature
is the fluid density at reference temperature 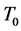 and
and 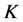 is the permeability of the porous medium. The wall temperature
is the permeability of the porous medium. The wall temperature 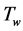 is assumed to be a constant. Most common fluids have dynamic viscosity that varies exponentially with temperature. Here we use Arrhenius model which takes the exponential form
is assumed to be a constant. Most common fluids have dynamic viscosity that varies exponentially with temperature. Here we use Arrhenius model which takes the exponential form
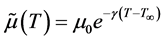
where ![]() is reference viscosity at reference temperature
is reference viscosity at reference temperature 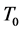 and
and ![]() is a viscosity variation number defined as
is a viscosity variation number defined as
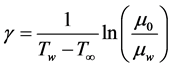
where  with be
with be 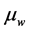 being the fluid viscosity at the wall temperature
being the fluid viscosity at the wall temperature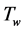 . For gases
. For gases 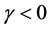 and for liquids it is positive. For small values of
and for liquids it is positive. For small values of ![]() Taylor expansion leads to the linear or the inverse relation of viscosity with temperature.
Taylor expansion leads to the linear or the inverse relation of viscosity with temperature.
Non-Similar Boundary Layer Equations
The equations are rendered non-dimensional by introducing a boundary layer pseudo-similarity variable 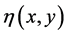 and a non-similar variable
and a non-similar variable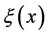 , defined respectively as
, defined respectively as
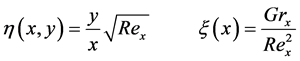
with 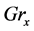 and
and 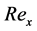 being the local Grash of number and the local Reynolds number, defined as
being the local Grash of number and the local Reynolds number, defined as
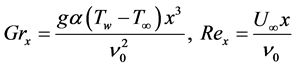
where 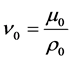 is the kinematic viscosity.
is the kinematic viscosity.
We use the scaling
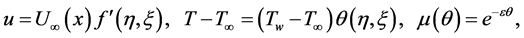
where  is the dimensionless viscosity and
is the dimensionless viscosity and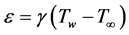 .
.
From the equation of continuity:
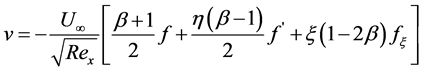
with
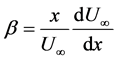
Assuming power law variation in the free-stream velocity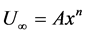 , we have
, we have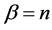 . The non-similar boundary layer equations take the form:
. The non-similar boundary layer equations take the form:
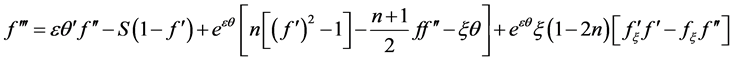 (2.4)
(2.4)
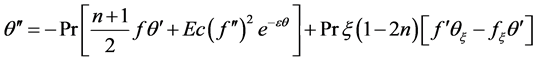 (2.5)
(2.5)
where ![]() is the dimensionless local permeability parameter,
is the dimensionless local permeability parameter, ![]() is the Prandtl number and
is the Prandtl number and  is the local Eckert number, defined respectively as
is the local Eckert number, defined respectively as
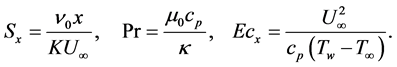
The boundary conditions, in non-dimensional form, are:
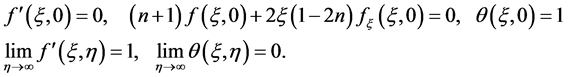 (2.6)
(2.6)
The shear stress and the heat transfer at the wall can be represented using the local skin friction coefficient and the local Nusselt number, defined by
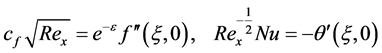
3. Numerical Solutions of the Non-Similar Boundary Layer Equations
The system of Equations (2.4)-(2.6) is solved using the non-similar method of Sparrow et al. [11] . This method has been used extensively in solving non-similar mixed convection boundary layer equations by among other Sparrow and Yu [12] , Gorla et al. [13] , Mureithi and Mason [14] , Bég et al. [15] etc. The method involves approximating the solutions at different levels of truncation. We introduce the notation:
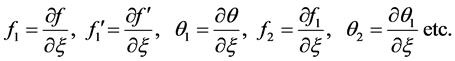
The first level of approximation involves solving the local similarity equations, where all terms involving the ![]() and its derivatives (that is the non-similar terms,
and its derivatives (that is the non-similar terms,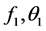 ) in the Equations (2.4)-(2.6) are neglected.
) in the Equations (2.4)-(2.6) are neglected.
At the second level of truncation, the method involves solving the system (2.4)-(2.6) together with the auxiliary system obtained by differentiating (2.4)-(2.6) partially with respect ![]() and neglecting all terms involving second order differentiation with respect to 𝜉 (that is
and neglecting all terms involving second order differentiation with respect to 𝜉 (that is 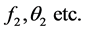 The auxiliary system takes the form:
The auxiliary system takes the form:
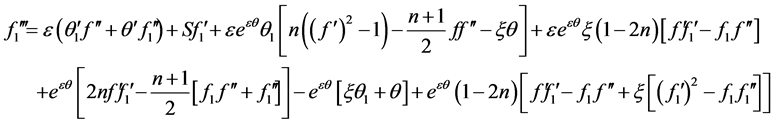 (2.7)
(2.7)
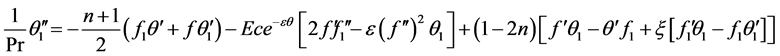 (2.8)
(2.8)
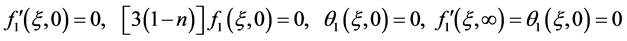 (2.9)
(2.9)
The system (2.4)-(2.9) solved as if it is an ordinary differential system, with ![]() being treated as a parameter. The results obtained are a better approximation than those obtained at the first level of approximation.
being treated as a parameter. The results obtained are a better approximation than those obtained at the first level of approximation.
An even better approximation can be obtained at the third order level of approximation, where the system (2.4)-(2.9) are solved together with an of auxiliary system obtained by further differentiating Equations (2.7)-(2.9) partially with respect to ![]() and all terms containing third order partials with respect to
and all terms containing third order partials with respect to ![]() are neglected.
are neglected.
4. Discussion of Results
We approximate the solution of (2.4)-(2.6) using the second level of approximation. The system of Equations (2.4)-(2.9) is solved using the fourth order Runge-Kutta method combined with a Newton root refinement scheme. Computations were carried out for the case when 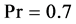 (air) and viscosity that increases exponentially with increase in temperature
(air) and viscosity that increases exponentially with increase in temperature .
.
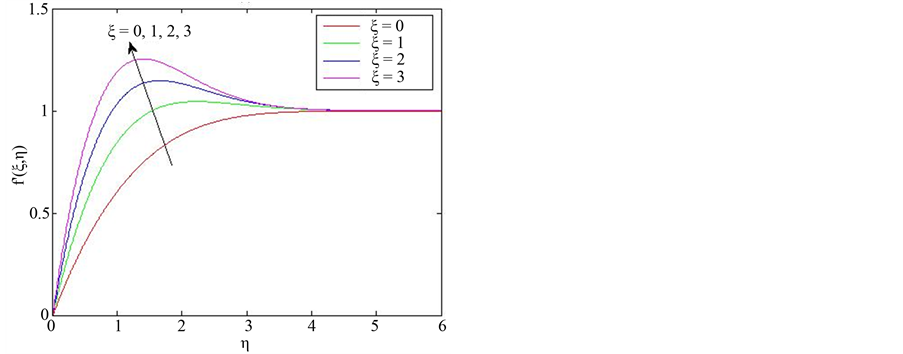
Figure 1 show the effect varying the non-similar parameter ![]() on the scaled stream-wise velocity,
on the scaled stream-wise velocity, ![]() , and viscosity,
, and viscosity,  , distribution in the boundary layer. At a fixed stream-wise location,
, distribution in the boundary layer. At a fixed stream-wise location, ![]() becomes a buoyancyrelated parameter. As
becomes a buoyancyrelated parameter. As ![]() increases velocity overshoots (exceeding free-stream velocity) are observed within the boundary layer. The maximum values of the super-velocities increase with increase in
increases velocity overshoots (exceeding free-stream velocity) are observed within the boundary layer. The maximum values of the super-velocities increase with increase in ![]() Results in figure 1also show that increasing
Results in figure 1also show that increasing ![]() has the effect of decreasing the thickness of the viscosity boundary layer.
has the effect of decreasing the thickness of the viscosity boundary layer.
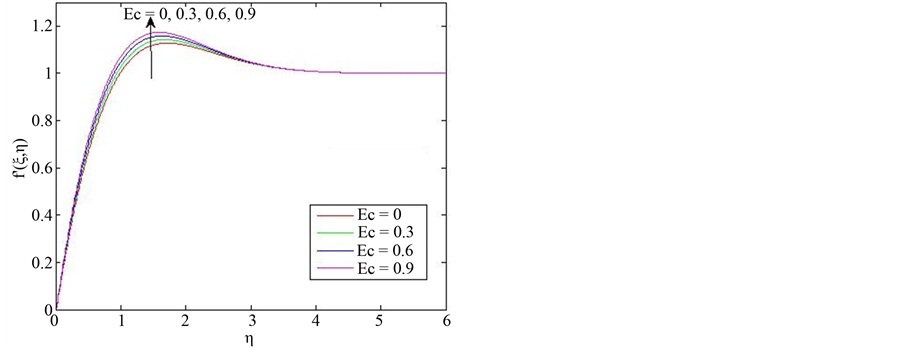
The effect of varying the viscous dissipation parameter 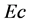 was investigated and the results are presented in Figure 2. The results indicate that as
was investigated and the results are presented in Figure 2. The results indicate that as 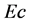 increases, the amplitude of the super-velocities increase. Temperature is also shown to increase with increase in
increases, the amplitude of the super-velocities increase. Temperature is also shown to increase with increase in 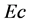 and for high enough values of
and for high enough values of  (in this case
(in this case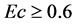 ) there is a small region adjacent to the wall, where temperature exceeds its wall value of one. It follows that viscosity function also has positive gradient in that small region. This is an indication that increasing
) there is a small region adjacent to the wall, where temperature exceeds its wall value of one. It follows that viscosity function also has positive gradient in that small region. This is an indication that increasing 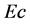 results in increased heat transfer from the wall to the fluid.
results in increased heat transfer from the wall to the fluid.
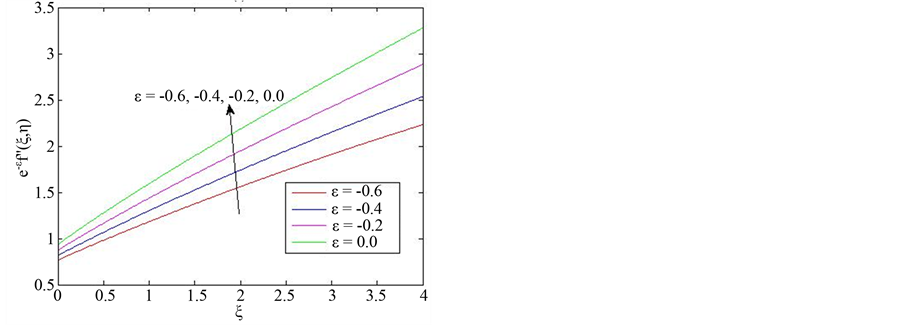
Figure 3 shows stream-wise velocity and viscosity distributions within the boundary layer for different values of![]() . The results show that at a fixed value of
. The results show that at a fixed value of ![]() velocity overshoots increase with increase in
velocity overshoots increase with increase in![]() . On the contrary, viscosity decreases with increase in
. On the contrary, viscosity decreases with increase in![]() .
.
Heat transfer at the wall (represented by the Nusselt number, 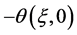 and shear stress at the wall (represented by skin friction coefficient,
and shear stress at the wall (represented by skin friction coefficient, 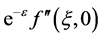 were investigated as functions of the effect of
were investigated as functions of the effect of ![]() and various values of
and various values of ![]() Figure 4 shows that the skin friction coefficient and Nusselt number increase with increase in
Figure 4 shows that the skin friction coefficient and Nusselt number increase with increase in![]() . The skin friction coefficient increases linearly with
. The skin friction coefficient increases linearly with ![]() while the Nusselt number decreases with increase in
while the Nusselt number decreases with increase in![]() .
.
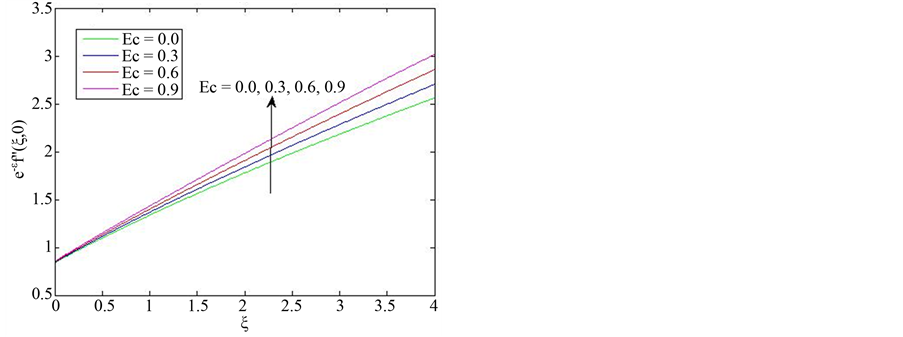
Similar results showing the effect of 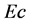 on both the skin friction and the Nusselt number are presented in Figure 5. The results show that the skin friction increases linearly with increase in
on both the skin friction and the Nusselt number are presented in Figure 5. The results show that the skin friction increases linearly with increase in ![]() while the Nusselt number decrease with increase in
while the Nusselt number decrease with increase in . On the other hand, increase
. On the other hand, increase 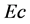 results in increase in the skin friction coeffi-
results in increase in the skin friction coeffi-
 (a)
(a)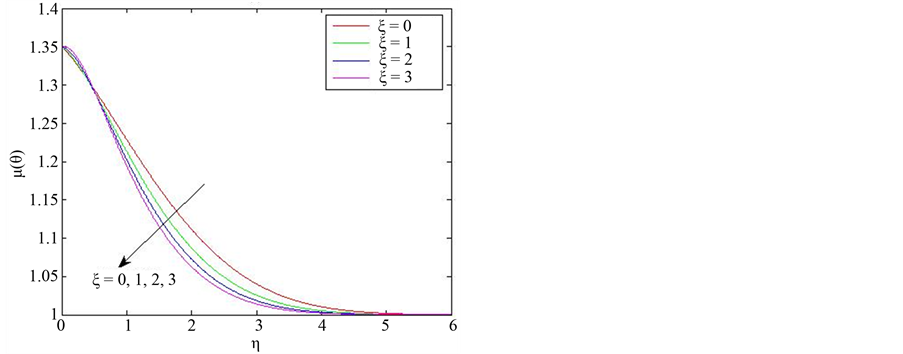 (b)
(b)
Figure 1. The effect of varying ![]() on (a) scaled stream-wise velocity
on (a) scaled stream-wise velocity ![]() and (b) viscosity
and (b) viscosity 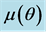 for the case when
for the case when
 (a)
(a)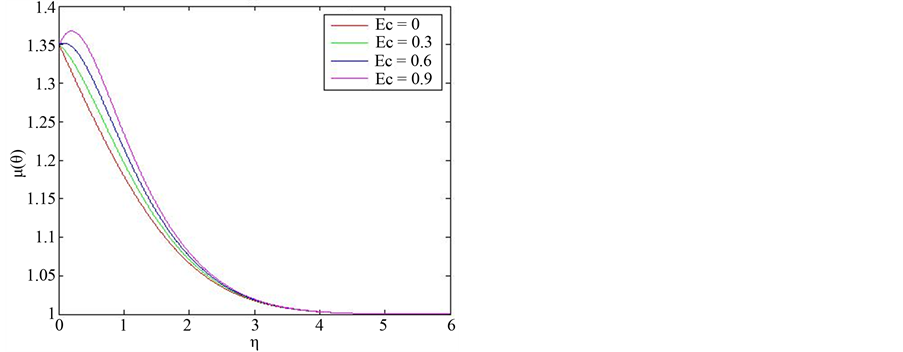 (b)
(b) (c)
(c)
Figure 2. Effect of varying  on (a)
on (a)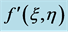 , (b)
, (b) 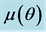 and (c)
and (c) 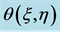 for the case when
for the case when 
![]()
 (a)
(a)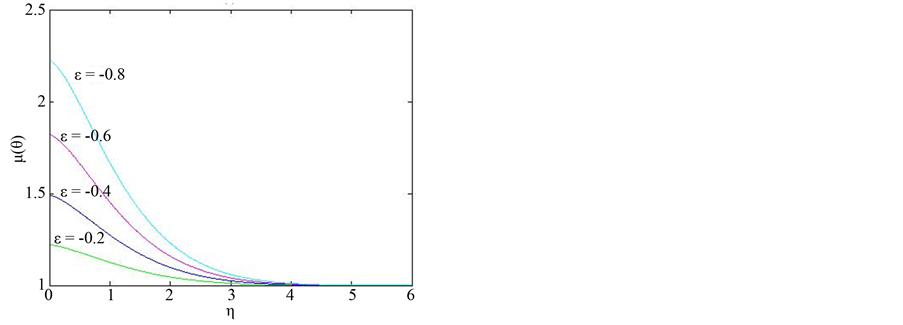 (b)
(b)
Figure 3. Effect of varying viscosity variation parameter ![]() on (a)
on (a) ![]() and (b)
and (b) 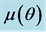 for the case when
for the case when 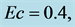

 (a)
(a)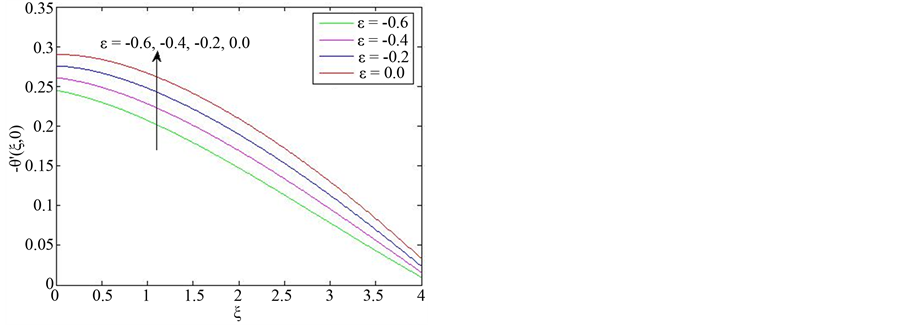 (b)
(b)
Figure 4. The effect of varying ![]() and
and ![]() on the (a) skin friction coefficient and (b) Nusselt number for
on the (a) skin friction coefficient and (b) Nusselt number for 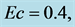

 (a)
(a)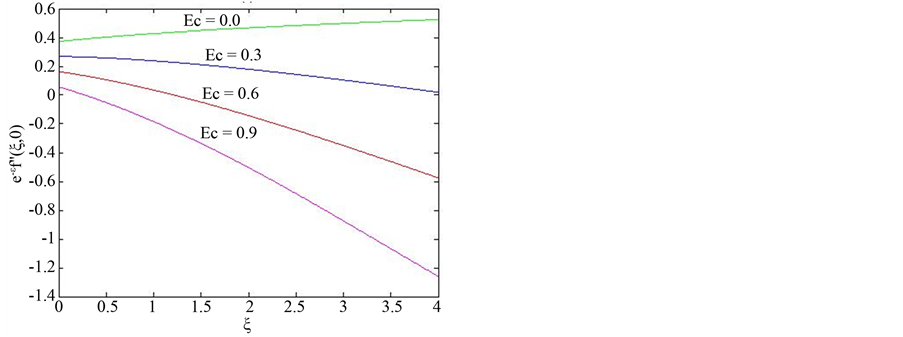 (b)
(b)
Figure 5. The variation of (a) skin friction coefficient and (b) Nusselt number with 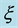 and
and ![]()
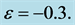
cient and a decrease in the Nusselt number. The results for the heat transfer coefficient indicate that at a fixed value of 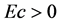 there is a critical value of
there is a critical value of 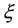 beyond which the heat transfer coefficient changes sign from positive (heat flows from fluid to the wall) to negative (heat flows from wall to the fluid in the boundary layer).
beyond which the heat transfer coefficient changes sign from positive (heat flows from fluid to the wall) to negative (heat flows from wall to the fluid in the boundary layer).
5. Conclusions
A non-Darcy mixed convection boundary layer flow has been investigated. The results have shown that the non-similarity parameter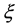 , which at particular stream-wise location represents thermal buoyancy, has the effect of accelerating the scaled free-stream velocity, resulting in super-velocities within the boundary layer. This effect is exacerbated by increasing viscous dissipation parameter and the viscosity variation parameter. The temperature dependent viscosity decreases with increase in buoyancy-related parameter and viscosity variation parameter but increases with increase in the viscous dissipation parameter.
, which at particular stream-wise location represents thermal buoyancy, has the effect of accelerating the scaled free-stream velocity, resulting in super-velocities within the boundary layer. This effect is exacerbated by increasing viscous dissipation parameter and the viscosity variation parameter. The temperature dependent viscosity decreases with increase in buoyancy-related parameter and viscosity variation parameter but increases with increase in the viscous dissipation parameter.
The skin friction coefficient increases with increase in the viscosity variation parameter, the viscous dissipation parameter and the buoyancy-related parameter. For flows with viscous dissipation effects, there is a critical value of the buoyancy related parameter, above which the Nusselt number changes sign from positive (wall extracts heat from fluid) to negative (fluid extracts heat from wall).
Acknowledgements
The author would like to thank the East African Universities Mathematics Programme (EAUMP) for their financial support.
References
- Nield, D.A. and Bejan, A. (2006) Convection in Porous Media. Springer and Business Media, New York.
- Pop, I.I. and Ingham, D.B., Eds. (2001) Convective Heat Transfer: Mathematical and Computational Modelling of Viscous Fluids and Porous Media. Elsevier Science & Technology Books, The Netherlands.
- Kaviany, M. (1995) Principles of Heat Transfer in Porous Media. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-4254-3
- Vafai, K., Ed. (2005) Handbook of Porous Media. Taylor & Francis, New York.
- Karabis, A., Kafoussias, N. and Xenos, M. (1995) Numerical Study of the Combined Forced-Free Convection Boundary Layer Flow through a Highly Permeable Porous Medium. Mechanics Research Communications, 22, 503-510. http://dx.doi.org/10.1016/0093-6413(95)00054-u
- Chen, C.H. (1998) Non-Similar Solutions for Non-Darcy Mixed Convection from a Non-Isothermal Horizontal Surface in a Porous Medium. International Journal of Engineering Science, 36, 251-263. http://dx.doi.org/10.1016/S0020-7225(97)00074-8
- Vafai, K. and Tien, C.L. (1981) Boundary and Inertia Effect on Flow and Heat Transfer in Porous Media. International Journal of Heat and Mass Transfer, 24, 195-203. http://dx.doi.org/10.1016/0017-9310(81)90027-2
- Hong, J.T., Tien, C.L. and Kaviany, M. (1985) Non-Darcy on Vertical Plate Natural Convection in Porous Media with High Porosities. International Journal of Heat and Mass Transfer, 28, 2149-2157. http://dx.doi.org/10.1016/0017-9310(85)90109-7
- Hossain, M.A. and Munir, M.S. (2000) Mixed Convection Flow from a Vertical Flat Plate with Temperature Dependent Viscosity. International Journal of Thermal Sciences, 39, 173-183. http://dx.doi.org/10.1016/S1290-0729(00)00237-4
- Jayanthi, S. and Kumari, M. (2007) Effect of Variable Viscosity on Non-Darcy Free or Mixed Convection Flow on a Vertical Surface in an Non-Newtonian Fluid Saturated Porous Medium. Applied Mathematics and Computation, 186, 1643-1659. http://dx.doi.org/10.1016/j.amc.2006.08.072
- Sparrow, E.M., Quack, H. and Boerner, C.J. (1970) Local Non-Similarity Boundary Layer Solutions. AIAA, 8, 1936-1942. http://dx.doi.org/10.2514/3.6029
- Sparrow, E.M. and Yu, H.S. (1971) Local Non-Similarity Thermal Boundary Layer Solutions. Journal of Heat Transfer, 93, 328-334. http://dx.doi.org/10.1115/1.3449827
- Gorla, R.S.R., Bakier, A.Y. and Byrd, L. (1996) Effects of Thermal Dissipation and Stratification on Combined Convection on a Vertical Surface Embedded in a Porous Medium. Transport in Porous Media, 25, 275-282. http://dx.doi.org/10.1007/BF00140984
- Mureithi, E.W. and Mason, D.P. (2010) Local Non-Similarity Solutions for a Forced-Free Boundary Layer Flow with Viscous Dissipation. Mathematical and Computational Applications, 15, 558-573.
- Bég, O.A., Bakier, A.Y., Prasad, V.R. and Ghosh, S.K. (2009) Non-Similar Laminar Steady Electrically Conducting Forced Convection Liquid Metal Boundary Layer Flow with Induced Magnetic Field Effects. International Journal of Thermal Sciences, 48, 1596-1606. http://dx.doi.org/10.1016/j.ijthermalsci.2008.12.007

