ABSTRACT

Received December 15, 2013; revised January 15, 2014; accepted January 21, 2014

The paper contains two parts. First, by applying the results about the eigenvalue perturbation bounds for Hermitian block tridiagonal matrices in paper [1], we obtain a new efficient method to estimate the perturbation bounds for singular values of block tridiagonal matrix. Second, we consider the perturbation bounds for eigenvalues of Hermitian matrix with block tridiagonal structure when its two adjacent blocks are perturbed simultaneously. In this case, when the eigenvalues of the perturbed matrix are well-separated from the spectrum of the diagonal blocks, our eigenvalues perturbation bounds are very sharp. The numerical examples illustrate the efficiency of our methods.

Keywords:

Singular Value; Eigenvalue Perturbation; Hermitian matrix; Block tridiagonal Matrix; Eigenvector

1. Introduction

There are many known results about eigenvalue perturbation bounds of Hermitian matrices. See example [2-5]. Among them, one well-known theory is the following result.

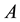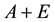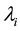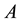Theorem 2.1 [2]. Let and be n-by-n Hermitian matrices. Let and denote the ith smallest eigenvalues of and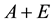, respectively. Then for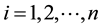, we have

(1.1)

where all the eigenvalues of 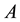and are indexed in ascending order.

This is the Weyl’s theorem, which is one of the most classic eigenvalue perturbation theories. When the perturbation matrix 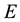is an arbitrary Hermitian matrix, the bounds obtained by Weyl’s theorem can be very small. However, for Hermitian matrices with special sparse structures such as block tridiagonal Hermitian matrix, the Weyl’s theorem may not be the best choice. For this reason, [1] considered the difference between eigenvalues of the block tridiagonal Hermitian matrices 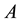and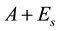, where

(1.2)

in which are Hermitian matrices and 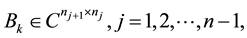are arbitrary

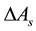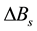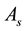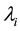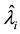matrices, the perturbation matrices and have the same order with the matrices and, respectively. Let and denote the ith smallest eigenvalues of matrices and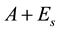, respectively. Let

denote the set of all the eigenvalues of the Hermitian matrix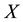. By defining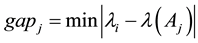, and assuming that there exists an integer such that, the

paper [1] obtained the shaper eigenvalue perturbation bounds

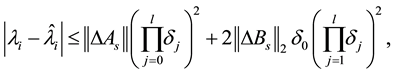(1.3)

in which

and

The natural questions are that whether the above results can be used to estimate the perturbation bounds for singular values of a block tridiagonal matrix, and how to get the eigenvalues perturbation bounds when two adjacent blocks of the matrix in the formula (1.2) are perturbed simultaneously. If we apply the results above repeatedly, we can obtain a weaker upper bounds. Inspired by these questions, in this paper, we expect to obtain the perturbation bounds for singular value of a block tridiagonal matrix. Further, we give a new idea to obtain the eigenvalues perturbation bounds by directly using the bounds of eigenvector elements rather than applying the results in [1] repeatedly.

The structure of this paper is organized as follows. In Section 2, we provide preliminaries to outline our basic idea of deriving eigenvalue perturbation bounds via bounding eigenvector components [1]. In Section 3, we present a new approach to estimate the perturbation bounds for the singular values of the block tridiagonal matrix via applying the ideas in paper [1]. In Section 4, we consider the case which the sth block and block of the matrix are perturbed simultaneously and present a new perturbation bound of the smallest eigenvalue. Further, we discuss the eigenvalue perturbation bounds when the first 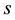blocks of 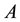are perturbed simultaneously and provide an algorithm to estimate the bounds. In Section 5, we present a numerical example to show the efficiency of our approach.

Notations. Let denote the matrix spectrum norm.

2. Preliminaries

For simplicity, the eigenvalues that we mention in this paper are all simple eigenvalues. We need the following conclusion about the partial derivative of simple eigenvalue of 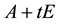for further discussion, where.

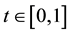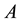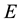Lemma 2.1 [1]. Let and be n-by-n Hermitian matrices. Denote by 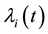the ith eigenvalue of

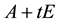, and define the vector-valued function 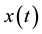such that 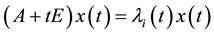where

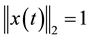
for some. If 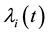is simple, then

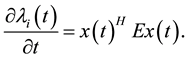(2.1)

Especially, the perturbation matrix 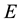has the special structure. For example, the perturbation matrix 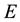has the form as the matrix 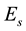whose block elements are zero except for the sth block. Moreover if 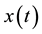has

small components in the positions corresponding to the nonzero elements of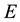, then 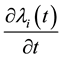is small. Hence

if we know a bound for the components of that are in the position corresponding to the nonzero elements

of, then we can obtain a bound for 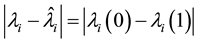via integrating the Equation (2.1) over.

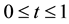Yuji Nakatsukasa [1] has derived the eigenvalues perturbation bounds for the case (1.2) with this idea. In the following, we shall describe in detail how this idea can be exploited to derive perturbation bounds of singular values for block tridiagonal matrix, and how this idea is expanded to derive eigenvalue perturbation bounds for our cases.

Note that the Lemma 2.1 holds under the condition that is a simple eigenvalue of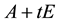. Similarly, we also assume that 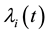is simple for all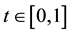. For multiple eigenvalues, we can discuss this case by referring to the method of the paper [1,6,7].

3. Singular Value Perturbation bounds

In this section, we use the results in paper [1] to study the perturbation bounds of singular values for the block tridiagonal matrices. For the sake of convenience, we define the sequence of nonzero singular values of a complex 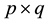matrix by

where and. Similarly, for the perturbation matrix, we denote the rank of by. Note that the nonzero eigenvalues of and are the same. Generally, the nonzero singular values of have important applications in many filed, so it's necessary to study singular value perturbation bounds. Just as the discussion of the [1,8] we only consider the simple singular values perturbation bounds.

3.1. 2 × 2 case

Firstly, for the case, we have the following results concerning the nonzero singular values perturbation bounds.

Theorem 3.1. Let

be two complex matrices, and be the nonzero singular values of

and, respectively. Define, and

. For, if and the ith singular value, then we have.

Proof. Let

(3.1)

and

(3.2)

By Jordan-Wielandt theorem[2-Theorem I.4.2], we know that the eigenvalues of the matrix are, where. The same statement holds for. Permuting the rows and columns of the matrix appropriately, we can get that the matrix is similar to

and the matrix is similar to

Let

Obviously, the matrix is a block Hermitian matrix, so is. Note that the, the eigenvalue set of is, and. So it is

natural that we can apply the result of [1-Theorem 3.2] to get the conclusion.

3.2. 3 × 3 case

Secondly, we study the perturbation bounds for singular values of case. Let

be two complex matrices, where and, and be the singular values of and, respectively. Similar to the discussion

above, by permuting the rows and columns of appropriately, we can get that the matrix is similar to

and the matrix is similar to

Obviously, both and are block tridiagonal Hermitian matrices. Applying [1-Theorem 4.2], we can get the following theorem.

Theorem 3.2. Let and be the ith smallest nonzero singular values of and, respec-

tively. Define, , and . For, if, then we have .

3.3. n × n Case

Further, we gradually consider the general case and extend above statements to the block tridiagonal matrices. Let

(3.4)

where and, and be the nonzero singular values of and, respectively. The following conclusion can be demonstrated.

Theorem 3.3. Let and be the ith smallest nonzero singular values of and, res-

pectively. Define, and. If there exists a positive integer such that, where, and

and

then we have

In what follows, we give an example to illustrate the singular values perturbation bounds obtained by our results.

Example 3.1. Consider the matrices and represented by

where

Obviously, the last two singular values of are. By computing, we can get that the two singular values of are

Therefore, we can get

(3.5)

Through the Theorem 3.1 we know that

By comparing the differences in the equation (3.5) with the bounds obtained by the Theorem 3.1, we can find that the singular values perturbation bounds obtained by the Theorem 3.1 are sharp and this estimating method is efficient.

4. Eigenvalue Perturbation Bounds

On the basis of conclusions of the paper [1], in this section we study eigenvalue perturbation bounds of block tridiagonal matrix for the cases where two adjacent blocks of are perturbed and the first blocks of are perturbed by the perturbation matrix.

4.1. Two adjacent blocks of A Being Perturbed

In this subsection, we discuss eigenvalue perturbation bounds when two adjacent blocks of are perturbed. In other words, we consider the matrices in the following form

(4.1)

Similar to discussion of the paper [1], we need the following assumption.

Assumption 1. There exists an integer such that, where

Roughly, the assumption demands that is far away from the eigenvalues of, respectively, and the norms of and are not too large.

Now, on the basis of the Assumption 1, we first discuss upper bounds for the eigenvector components of the matrix.

Lemma 4.1. Let and be Hermitian block-tridiagonal matrices in (4.1), be the ith smallest

eigenvalue of. For, let, where and

satisfying that and have the same number of rows. Define

and for,

(4.2)

If satisfies Assumption 1, then, for all we have

(4.3)

Proof. The first block component of is

Since for, by Weyl’s theorem,

we have. Therefore, we have

Further, by applying the Theorem 2.1[2], we know and

. So we can bound by

(4.4)

where the right inequality follows from Assumption 1. Continuously, the second block component of

is

So,

Similarly, by Weyl's theorem, we have. Combining this inequality with

(4.4), we can get

Hence,.

By the same argument, we can prove for all

To consider the sth block component of, we have

thus,

By using the results of the Assumption 1 and Theorem 2.1[2], we know that is invertible

and. Since, we can get

Therefore, for all we can obtain the following result

Continuously, considering the s + 1^th block of,

we have

Similarly, by using the results of the Assumption 1 and Theorem 2.1[2], we know that

is invertible and. Since, for all

, we can get

Hence,

Similar to the discussion above, we also have

By and, we have

Consequently, for all,

Similar to the discussion above, we can prove. In addition,.

Based on the discussion above, we conclude that for all,

The following Theorem 4.1 is aiming to present perturbation bounds for.

Theorem 4.1. Let and be the smallest eigenvalues of matrix and, respectively, and be defined as in (4.2). If satisfies the Assumption 1, we have

Proof. Integrating (2.1) over we get

Together with (4.3), it follows that

4.2. The first s blocks of A Being Perturbed

In this subsection, we gradually consider the bounds of eigenvalues of the matrix, whose the first blocks are perturbed simultaneously. In other words, we consider the perturbation matrix

(4.5)

where is a positive integer.Let denote the ith eigenpair of satisfying

, and the partition of satisfies that

and have the same number of rows, where.

If satisfies the Assumption 1, through the similar discussion as above, we can derive a similar conclusion for calculating the eigenvalue perturbation bounds. For simplicity, we don't repeat the proof here. The Algorithm 1 below shows the calculation in detail, where, and.

5. Numerical Example

In this section, we use the following example to illustrate the validity of our method and to show the advantage of the our method over the method proposed in [1].

Example 5.1 [1]. Let be the tridiagonal matrix

(5.1)

Algorithm 1. Eigenvalue perturbation bound algorithm for the first s blocks of being perturbed.

where all the elements of are zero except for the 900th and 901th off diagonal, which are 1. Note that none of the off-diagonals is negligibly small. We focus on (the ith smallest eigenvalue of) for, which are smaller than 10. For such we have, and give bounds for with our method. The results are outlined in Table 1.

Meanwhile, we use the method in the paper [1] to give the perturbation bounds for. The results are outlined in Table 2.

Further, we partition the matrix as in the (5.1) again so that the block size is one except for the 900th

block, which is 2-by-2 matrix. In other words, we set, , and set, (i.e., s = 900). Using the method in the paper [1] we have the following

perturbation bounds for, which are outlined in Table 3.

Obviously, comparing the table 1 with the table 2, we can see that our method saves CPU times and improves the perturbation bounds. In addition, comparing the table 1 with the table 3, although our CPU time is close to the CPU time in Table 3, we see that the perturbation bounds are also improved . So we can say that our method is efficient and improved.

6. Conclusion

We have obtained a new efficient method to estimate the perturbation bounds for singular values of block tridiagonal matrix. Further, under the bases of the paper [1], we present a new conclusion for estimating the perturbation bound when the sth block and block of the matrix are perturbed simultaneously and

provide an algorithm for the general case when the first blocks of are perturbed simultaneously. Number examples are presented to show the effectiveness of our methods.

References

NOTES

^*The work was supported by the Fundamental Research Funds for the Central Universities (xjj20100114) and the National Natural Science Foundation of China (11171270).

^#Corresponding author.