Open Journal of Modern Hydrology
Vol. 3 No. 3 (2013) , Article ID: 34119 , 11 pages DOI:10.4236/ojmh.2013.33019
Development of Pedotransfer Functions for Saturated Hydraulic Conductivity
![]()
1Department of Environmental and Biosystems Engineering, University of Nairobi, Nairobi, Kenya; 2Department of Earth and Environmental Science and Technology, Technical University of Kenya, Nairobi, Kenya.
Email: jobiero@uonbi.ac.ke
Copyright © 2013 John P. O. Obiero et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 24th, 2013; revised April 24th, 2013; accepted May 3rd, 2013
Keywords: Pedotransfer Functions; Development; Evaluation
ABSTRACT
The purpose of the study was to develop pedotransfer functions for determining saturated hydraulic conductivity (Ks). Pedotransfer functions (PTFs) for predicting soil physical properties used in determining saturated hydraulic conductivity, based on moisture retention characteristics, were developed. The van Genuchten moisture retention equation was fitted to measured moisture retention properties obtained from International Soil Reference and Information Centre (ISRIC) soils data base in order to determine parameters in the equation i.e. saturated soil moisture content (θs), residual soil moisture (θr), air entry parameter (α) and the pore size distribution parameter (n). 457 samples drawn from the data base were used to be the maximum possible sample size that contained the measured soils characteristics data required. Using statistical regression, mathematical relationships were developed between moisture retention parameters (response variables) and appropriately selected transformed basic soil properties (predictor variables). The developed PTFs were evaluated for accuracy and reliability. It was found that pedotransfer functions developed for θs produced the best performance in reliability compared to the remaining parameters yielding a correlation coefficient value of coefficient of determination (R2 = 0.76), RMSE = 2.09, NSE = 0.75 and RSR = 0.5 indicating good performance. Relatively poorest performance was obtained from the pedotransfer function developed for α which yielded a correlation coefficient, R2= 0.06, RMSE = 0.85 and a NSE of 0.02 reflecting the best possible equation derived for the parameter for use in predicting hydraulic conductivity. Out of the pedotransfer functions developed for each of the moisture retention parameters, the best performing PTF was identified for each parameter. The accuracy of the pedotransfer functions assessed based on R2 were for θs (R2 = 0.80), θr (R2 = 0.42), α (R2 = 0.04) and for n (R2 = 0.30), when the variables were expressed directly in terms of the selected transformations of the basic soil properties.
1. Introduction
Hydraulic conductivity is an important parameter that influences hydrological processes which affect flow in rivers. For instance, ground water flow is determined by saturated hydraulic conductivity (Ks). A number of formulations have been developed over the years to predict soil hydraulic conductivity from readily measurable soil properties. The need for mathematical modeling of Ks arises from the fact that insitu or laboratory measurements of hydraulic conductivity are time consuming, labour intensive and expensive as noted by [1], making it practically unlikely in reality to collect permeability data. Besides, direct measurements are also unreliable for site specific applications. The use of pedotransfer functions is an alternative to determining hydraulic conductivity and involves relationships that enables Ks to be predicted using measurable soil physical and hydraulic properties. Ks serves as an input parameter in many hydrological models. There is no specific method considered most accurate in determining Ks as the method used depends on soil and environmental conditions. Furthermore, data on Ks is not readily available in most local soil survey data bases and even where they are available, the reliability is not guaranteed. There is uncertainty in the prediction of Ks using existing pedotransfer functions. Methods to develop PTFs are also unknown and not well understood especially in Africa. Well known moisture characteristic functions are based on parameters that can be determined using moisture retention characteristics. Such data is not readily available in most soil data bases. It is essential to estimate such parameters using basic and easily available soil properties like bulk density, texture etc. Attempts to develop such equations is rare.
[2] notes that modern simulation and analysis of hydrologic processes relies heavily on the accurate and reliable description of soil water holding and transmission characteristics. Predicting Ks from basic soil properties using developed pedotransfer functions is based on analysis of the existing data sets, an approach applied in agricultural hydrology and watershed management. This research demonstrates how pedotransfer functions can be developed from a data base, with limited soils data, in predicting van Genuchten moisture retention parameters, a step in predicting Ks from readily available data on basic soil properties available from soil survey data. Ks can be indirectly predicted from soil properties using moisture retention equations like van Genuchten, Brooks Corey etc. where data on moisture retention curves is available. This technique was used in the study. Readily available data on measured Ks is rare and characterized with uncertainty on their accuracy as different methods in different environments yield varied results as observed by [3] therefore necessitating use of the indirect methods.
Three types of pedotransfer functions are recognized [4]. One category predicts soil moisture retention from basic soil properties. The other is based on point prediction of water retention characteristic as used by [5] to predict points along the moisture retention curve on Iranian soil. Another category involves prediction of parameters in models describing the θ-h-k relationship. This latter approach used in the study involved pedotransfer functions that relate the simple and easy to measure soil properties to van Genutchen moisture retention parameters, a notable gap in the science of development of pedotransfer functions. Most established pedotransfer functions for predicting soil hydraulic characteristics from continuous soil properties are based on statistical regression [6] in which the response variable, y, predicted from a number of n predictor variables, xi yields the statistical multiple linear regression tool expressed as
 (1)
(1)
where “a” is the intercept, bi is the regression coefficient and ε is the error. The procedure to develop the pedotransfer functions involves steps which include:
The first step of statistical analysis is intended to test if each response variable distribution may be considered as normal distribution [7]. The normality of a distribution is tested by certain statistics like the Shapiro-Wilk (Wvalue), Skewness coefficient and Kurtosis. The shape of the distribution is determined by a measure of its Skewness which is given by the equation,
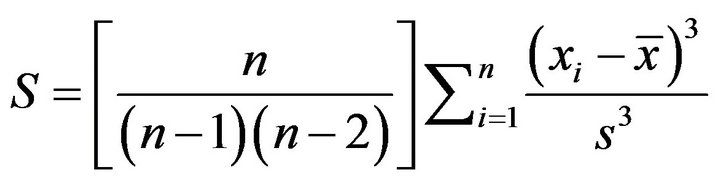 (2)
(2)
where S is Skewness coefficient, s the standard deviation, xi the observation value, ![]() the mean value and n the number of observations. For a normally distributed data, the skewness = 0, hence the closer the skewness coefficient is to zero (0), the better the normality of the distribution. The level of Kurtosis also provides information about the extent of the normality of the distribution and is given by,
the mean value and n the number of observations. For a normally distributed data, the skewness = 0, hence the closer the skewness coefficient is to zero (0), the better the normality of the distribution. The level of Kurtosis also provides information about the extent of the normality of the distribution and is given by,
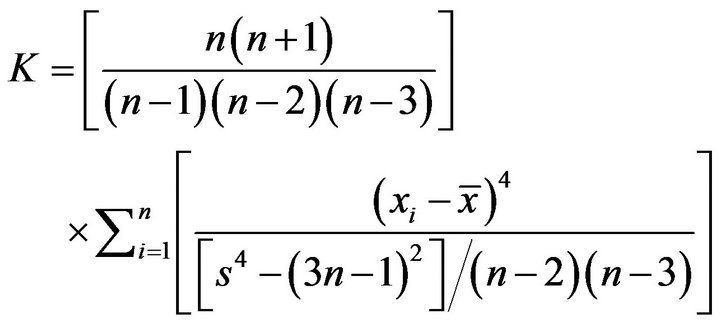 (3)
(3)
The measure of Kurtosis is zero (0) for a normally distributed population. Graphical aids used to check normality includes the normal probability plot.
Mathematical relationships between potential predictor variables and the response variables are checked by detecting exponential, logarithmic, or square root tendencies. Important to eliminate is the problem of redundant information in the predictor set brought about by linear dependence between predictor variables [6]. This problem of multicollinearity can be examined by means of correlation matrix. Common statistics used in evaluating pedotransfer functions include [4]:
Multiple determination coefficient given by
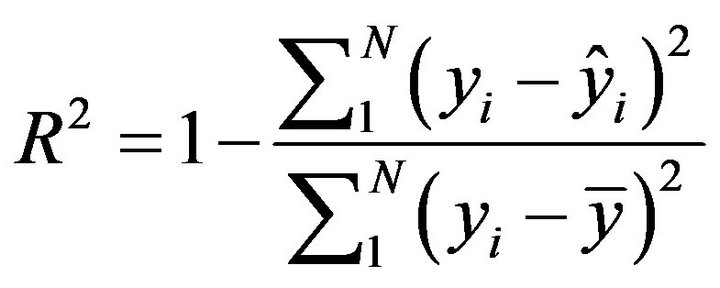 (4)
(4)
Root mean square error given by
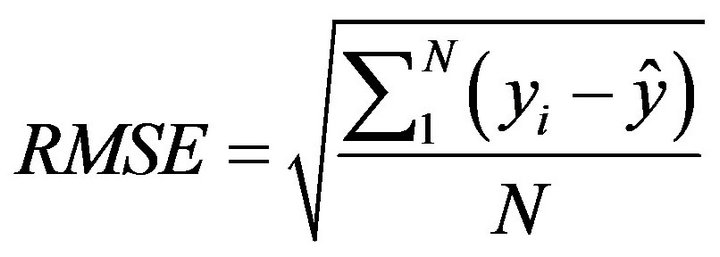 (5)
(5)
Mean Error given by
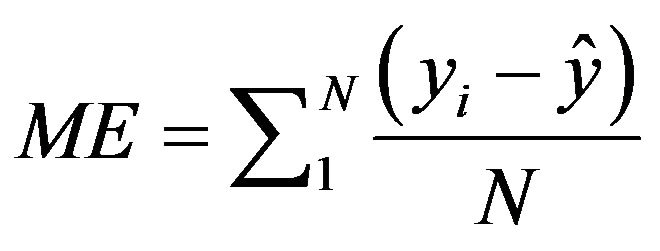 (6)
(6)
Mean Absolute Error given by
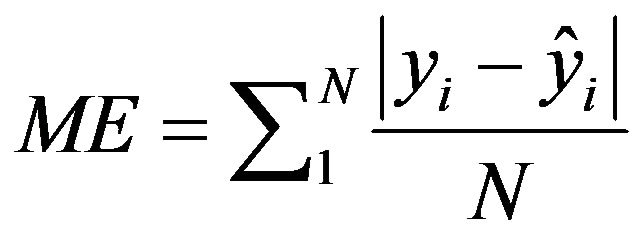 (7)
(7)
where yi denotes the actual value, 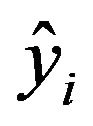 the predicted value, and
the predicted value, and ![]() the average of the actual value and N is the total number of observations. [8] evaluated performance of different pedotransfer functions for estimating certain soil hydraulic properties that include Available Water Capacity (AWC) using R2, RMSE and ME. [9] used only RMSE in assessing pedotransfer functions developed for predicting hydraulic conductivity and water retention.
the average of the actual value and N is the total number of observations. [8] evaluated performance of different pedotransfer functions for estimating certain soil hydraulic properties that include Available Water Capacity (AWC) using R2, RMSE and ME. [9] used only RMSE in assessing pedotransfer functions developed for predicting hydraulic conductivity and water retention.
The van Genuchten water retention equation which relates moisture content (θ) to the soil matric suction (h) and is expressed as follows;
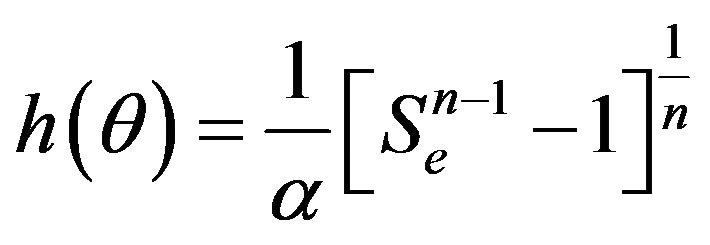 (8)
(8)
where
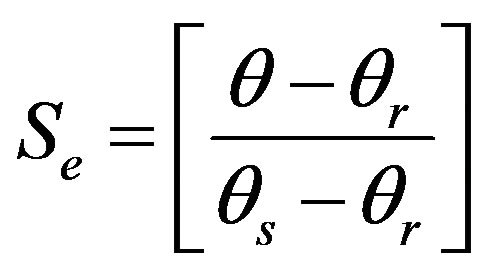 (9)
(9)
To determine Ks, the hydraulic conductivity function used is expressed as
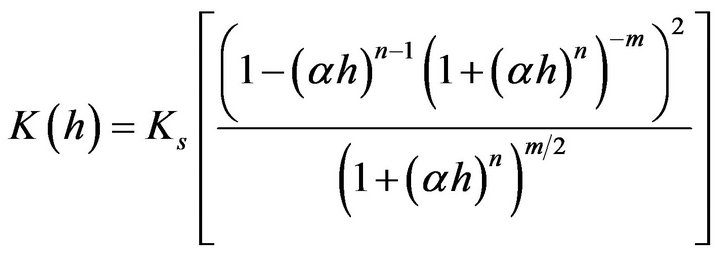 (10)
(10)
To determine Ks using the above equation, a relationship between hydraulic conductivity and matric suction, h is used and can be obtained through equations that relate hydraulic conductivity to permeability [10].
2. Methodology
2.1. Data Collection and Analysis
[4] noted that data from existing international soil data bases having measured soil data can be analyzed to enable prediction of hydraulic characteristics from measured soil data. Availability of measured soil hydraulic characteristics for a wide range of soils and from a large and reliable international data bases are considered prerequisite for development of pedotransfer functions. The ISRIC soils database was used to obtain measured data on soil hydraulic characteristics and basic soil properties. It was possible to obtain all the required measured data on 457 soil samples from various parts of the world. The data contained measured moisture retention curves as well as data on texture (Sand%, Clay% and Silt%). The ISRIC dataset [11] was used for this test. This dataset contains Water Retention Curve (WRC) for both topsoil (between 0 and 20 cm depth) and subsoil (between 20 and 100 cm) from many countries in the world. It has 8 levels of measured suction potential (at 0, 0.1, 0.312, 1.0, 1.99, 5.01, 2.5, and 15.8 m) (Figure 1). The lowest suction potential was taken as 0.01 to avoid errors with logarithmic transformations. The observed moisture retention curve obtained from measured data on moisture retention characteristics was fitted to the van Genuchten moisture retention Equation (11)
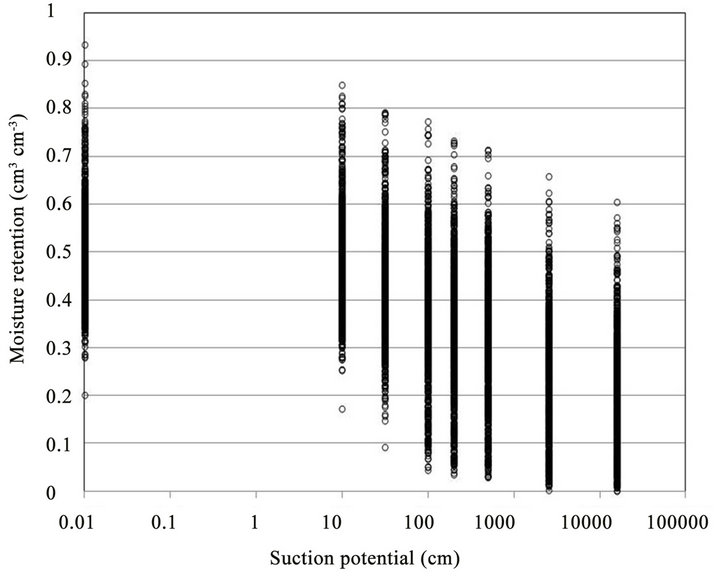
Figure 1. Measured water retention characteristics from ISRIC database.
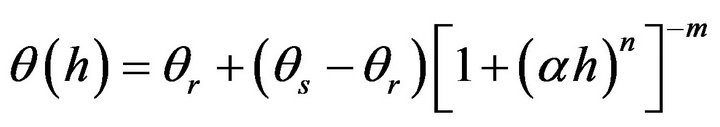 (11)
(11)
where q(h) is the soil moisture content at h suction potential, qr is the residual moisture content, qs is the saturated moisture content, a is the inverse of air-entry potential, and n and m are the shape parameters for the water retention curve representing pore-size distribution index [12]. HydroMe computer programme was used to determine parameters of the van Genuchten equation (http://cran.r-project.org/web/packages/HydroMe/index.html) and is executable in R programme The pedotransfer functions were then developed to estimate these parameters from readily available measured basic soil properties. Relating the moisture retention parameters to the basic soil properties then makes it possible to predict the moisture retention characteristics from the basic properties and hence enabling prediction of the saturated hydraulic conductivity. It would therefore not be necessary to have measured data on moisture retention characteristics to determine Ks but instead, the basic soil properties would be used in determining the equations for moisture retention which can then be used to estimate Ks. Measurement of moisture retention characteristics is quite elaborate, tedious, time consuming and also expensive especially if a large number of sites is involved. From the sample data set of 457 samples, a sub dataset consisting of 342 (75%) samples was randomly selected for use in calibration of the pedotransfer functions to be developed while the remainder portion of 115 samples (25%) of the data was used in the validation process. In development of the pedotransfer functions, the following procedures were undertaken.
2.1.1. Evaluation of the Distribution of the Moisture Retention Parameters
A requirement in developing pedotransfer functions is that the response (dependent) variables should be normally distributed. As a result, the moisture retention parameter of the van Genuchten equation and their possible transformations were evaluated to establish which would best approximate normal distribution. To check the extent to which the response variables would be normally distributed, statistical measures of Shapiro Wilk (W-value), Skewness Coefficient, and measures of Kurtosis were used in the assessment.
2.1.2. Statistical Regression Analysis
Statistical regression was performed between each transformed response variable and each of the basic properties and their transformations so as to establish the goodness of fit in each case based on the measure of the coefficient of determination (R2). The purpose of this was to determine, for each response variable, the predictor variable or its transformation that gives the best quality of fit between the two when a regression is performed. This would give an indication of which predictor variable or its transformation correlates best with the response variable or it transformation.
2.1.3. Analysis of Cross Correlations
To establish the level of dependence between the selected predictor variables for each response variable best correlated to them, a cross correlation was performed between the independent variables by determining the correlation coefficient (r) between each pair of the vari ables. This kind of analysis is performed to determine if there is any correlation between two predictor variables among the set chosen for determining the multiple regression equations. It is preferable that the independent variables in a multiple linear regression equation be independent among themselves.
2.1.4. Multiple Linear Regression and Validation of Developed Equations
This was carried out between each selected transformed response variable and selected combination of predictor variables/transformation consisting of the independent variables for which the response variable best correlated as determined by the measure of coefficients of determination. The multiple coefficient of determination was determined for each equation developed to assess the accuracy of the equation. The multiple regression was carried out between response variables and the predictor variables or transformations consisting of independent variables that are not themselves significantly correlated (r < 0.5). After development of the pedotransfer functions using the given data set, their reliability is then tested by comparing the values of predicted parameters using the developed equations with the observed data using an independent data set. An independent data set consisting of 115 samples was used in the validation process. The evaluation statistic used included the correlation coefficient among others.
3. Results and Discussion
3.1. Evaluation of the Distribution of the Moisture Retention Parameters
Table 1 shows the values of statistical parameters used for evaluating normality of distribution for the response variables being the van Genuchten moisture retention parameters and their proposed transformations for the data set of 457 samples. The transformations of van Genuchten parameters (response variables) that produced the best approximation to normal distribution are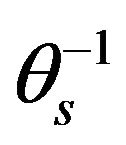 ,
, 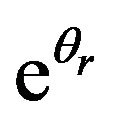 ,
, 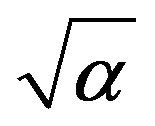 and
and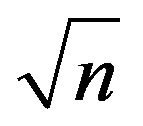 . This was based on measures of the ShapiroWilk (W-value), Skewness coefficient and Kurtosis. For illustration, Figure 2 shows the histogram and normality plot in the normal distribution check for the saturated soil moisture content transformation (θs).The transformations of van Genutchen parameters (response variables) that produce the best approximation to normal distribution are
. This was based on measures of the ShapiroWilk (W-value), Skewness coefficient and Kurtosis. For illustration, Figure 2 shows the histogram and normality plot in the normal distribution check for the saturated soil moisture content transformation (θs).The transformations of van Genutchen parameters (response variables) that produce the best approximation to normal distribution are ,
, 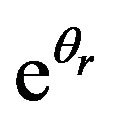 ,
, 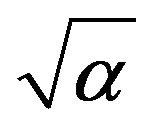 and
and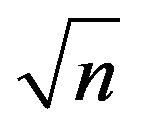 . This was based on measures of the Shapiro-Wilk (W-value), Skewness coefficient and Kurtosis.
. This was based on measures of the Shapiro-Wilk (W-value), Skewness coefficient and Kurtosis.
3.2. Statistical Linear Regression Analysis
The quality of fit for the linear regression between each

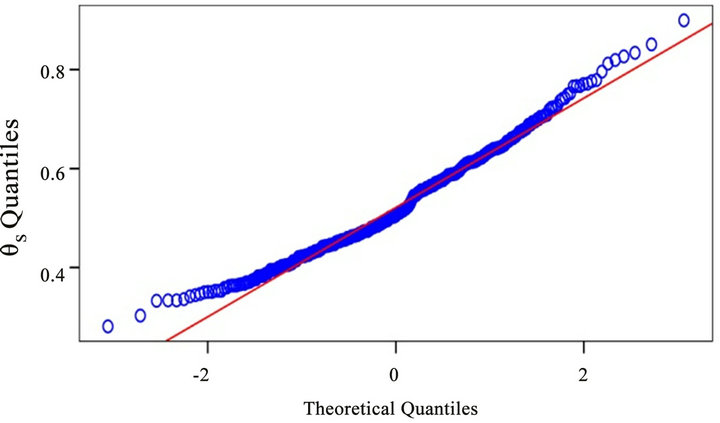
Figure 2. Check for normality of distribution of the saturated soil moisture content (θs) showing the histogram and normality plot.
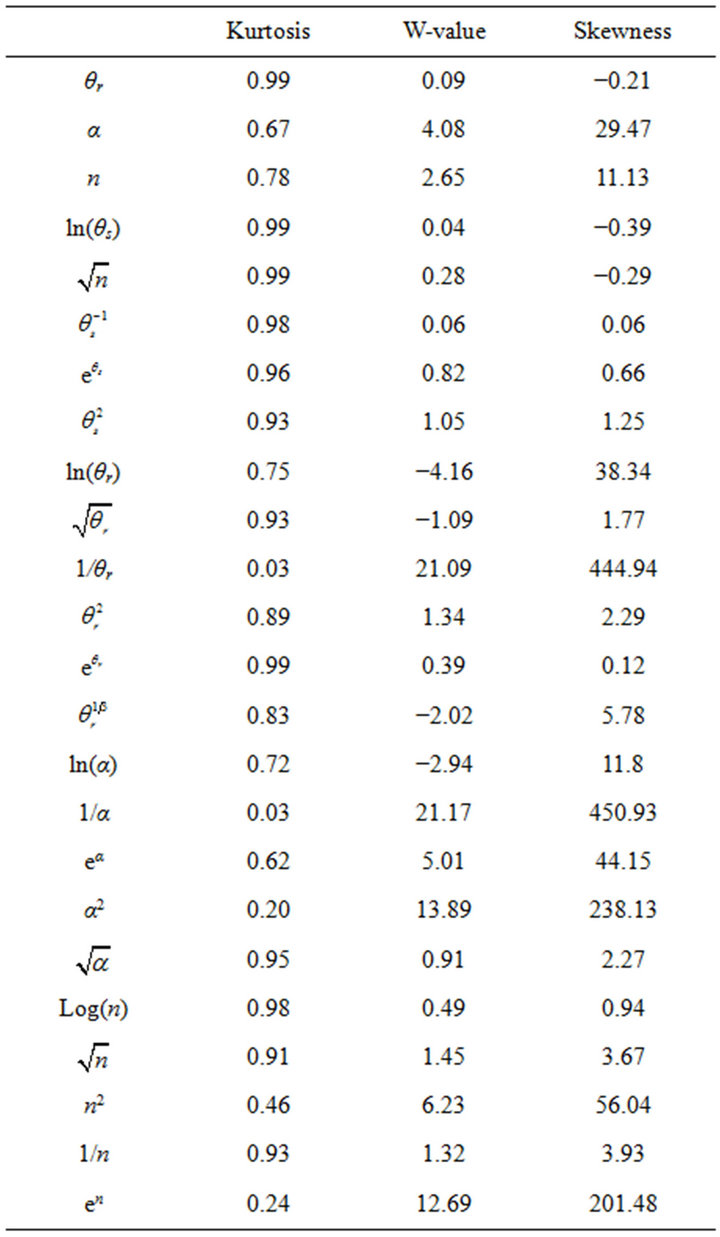
Table 1. Normality of distribution check for parameters in the van Genuchten water retention characteristic and their transformations.
selected transformed dependent variables (moisture rention parameters) and the transformed independent variables (basic soil properties) was notably different for each predictor variable transformation. For instance, the linear regression performed between θs and sand yielded a quality of fit, measured by the value of R2, to be 0.10 while that between θs and esand yielded R2 = 0.01 (Table 2). The same observation was made in the case of regreson performed with silt, clay, bulk density and organic carbon. Also each selected transformed variable (i.e. ln(θs), 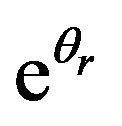 ,
, 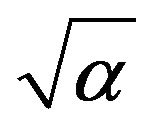 , etc.) produced different values of R2 when a linear regression was performed between each of the response variables and a transformed predictor varile for each of the variables sand, silt, clay bulk density and organic carbon. For example, a regression performed between the independent variable sand2 and
, etc.) produced different values of R2 when a linear regression was performed between each of the response variables and a transformed predictor varile for each of the variables sand, silt, clay bulk density and organic carbon. For example, a regression performed between the independent variable sand2 and  yielded R2 = 0.14 while that between sand2 and
yielded R2 = 0.14 while that between sand2 and 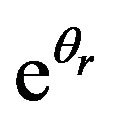 produced R2 = 0.20, hence no particular transformed variable could be said to generally give the best quality of fit with all the dependent variables whether it is sand, silt, clay, bulk density or organic carbon. Also, there is no particular response variable that could be said to yield the best quality of fit compared to others for all the independent variables or transformations to which regression was performed. The purpose of regression analysis was to identify the pair of transformed dependent and independent variables that yield the best quality of fit between them as measured by coefficient of determination (R2) so that for each dependent variable, one is able to identify which transformations of each of the dependent variables would be used in developing the pedotransfer functions during multiple regression equation to relate each response variable and selected predictor variables and appropriate transformations. This would help establish the best possible mathematical relationship between the moisture retention parameters (response variables) and selected
produced R2 = 0.20, hence no particular transformed variable could be said to generally give the best quality of fit with all the dependent variables whether it is sand, silt, clay, bulk density or organic carbon. Also, there is no particular response variable that could be said to yield the best quality of fit compared to others for all the independent variables or transformations to which regression was performed. The purpose of regression analysis was to identify the pair of transformed dependent and independent variables that yield the best quality of fit between them as measured by coefficient of determination (R2) so that for each dependent variable, one is able to identify which transformations of each of the dependent variables would be used in developing the pedotransfer functions during multiple regression equation to relate each response variable and selected predictor variables and appropriate transformations. This would help establish the best possible mathematical relationship between the moisture retention parameters (response variables) and selected
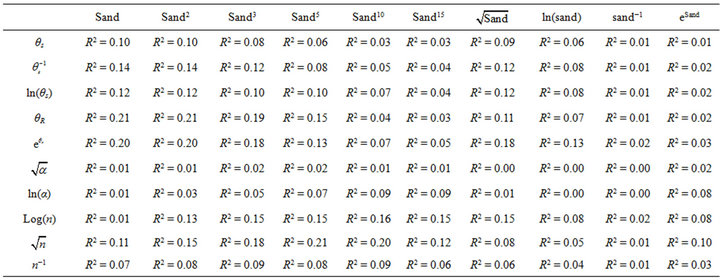
Table 2. Measurement of the quality of fit based on coefficient of determination (R2) between the moisture retention parameters (response variable) and sand with its transformation (predictor variables) in the linear regression.
basic soil properties (independent variables) in the pedotransfer function. A number of observations on the regression relationships can be made for each response variable and how it relates with each of the predictor variables and their transformations. The transformed response variable  yielded the best quality of fit (R2 = 0.14) with the independent variables sand or sand2 compared to the other transformations when a regression analysis was performed. In the case of regression with silt, the best possible quality of fit was obtained with the transformation silt−1 (R2 = 0.04) and so was with bulk density, BD3 (R2 = 0.60),
yielded the best quality of fit (R2 = 0.14) with the independent variables sand or sand2 compared to the other transformations when a regression analysis was performed. In the case of regression with silt, the best possible quality of fit was obtained with the transformation silt−1 (R2 = 0.04) and so was with bulk density, BD3 (R2 = 0.60), 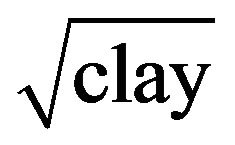 or clay2 (R2 = 0.12), organic carbon, ln(orgC) (R2 = 0.27). In general, the linear regression performed between
or clay2 (R2 = 0.12), organic carbon, ln(orgC) (R2 = 0.27). In general, the linear regression performed between 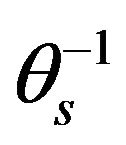 and the bulk density transformations produced best quality of fit as compared to those of silt, sand, organic carbon and clay, showing that the best relationship was obtained with bulk density followed by organic carbon, sand, clay and silt in that order. In the case of residual moisture content, θr , the selected transformation variable
and the bulk density transformations produced best quality of fit as compared to those of silt, sand, organic carbon and clay, showing that the best relationship was obtained with bulk density followed by organic carbon, sand, clay and silt in that order. In the case of residual moisture content, θr , the selected transformation variable  related best with clay with a quality of fit R2 = 0.32 obtained when regression was performed between
related best with clay with a quality of fit R2 = 0.32 obtained when regression was performed between 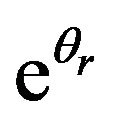 and
and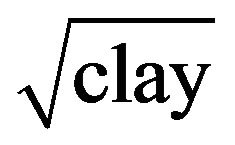 . The poorest fit was obtained when the regression was performed with transformations of organic carbon e.g. ln(orgC) with R2 = 0.01. α yielded the best possible quality of fit when a regression was performed with
. The poorest fit was obtained when the regression was performed with transformations of organic carbon e.g. ln(orgC) with R2 = 0.01. α yielded the best possible quality of fit when a regression was performed with 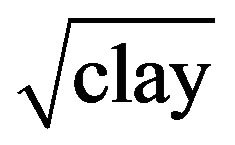 or 1/clay.
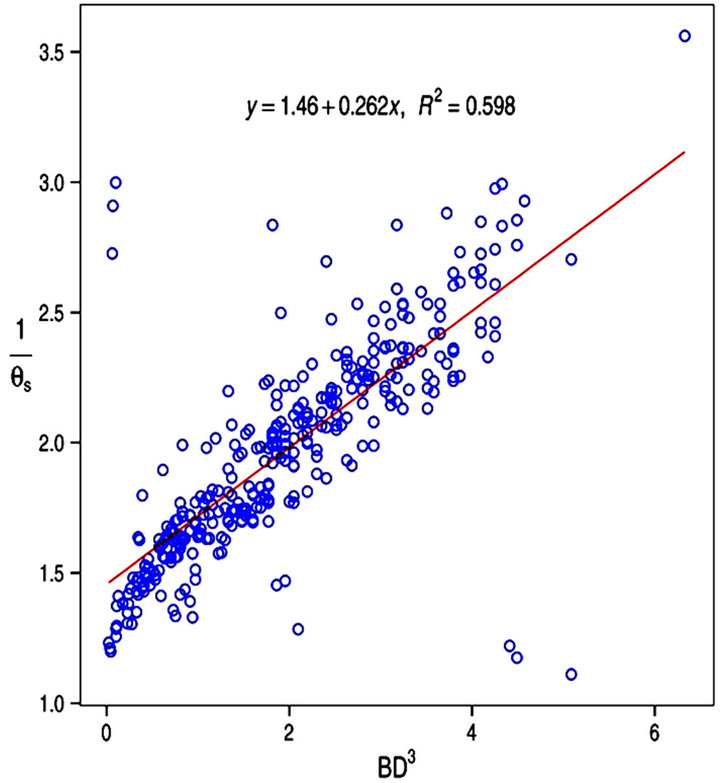
or 1/clay. 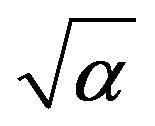 generally showed poor quality of fit with most of the independent variables or transformations. The transformation n−1 also showed poor quality fit with most of the selected response variables when regression analysis was performed. The best quality fit was obtained with the transformation of sand when the linear regression was performed between n−1 and sand3 (R2 = 0.09). Figures 3(a)-(d) illustrates the regression between selected transformations of response variables and the predictor variables to which they best fit.
generally showed poor quality of fit with most of the independent variables or transformations. The transformation n−1 also showed poor quality fit with most of the selected response variables when regression analysis was performed. The best quality fit was obtained with the transformation of sand when the linear regression was performed between n−1 and sand3 (R2 = 0.09). Figures 3(a)-(d) illustrates the regression between selected transformations of response variables and the predictor variables to which they best fit.
 (a)
(a)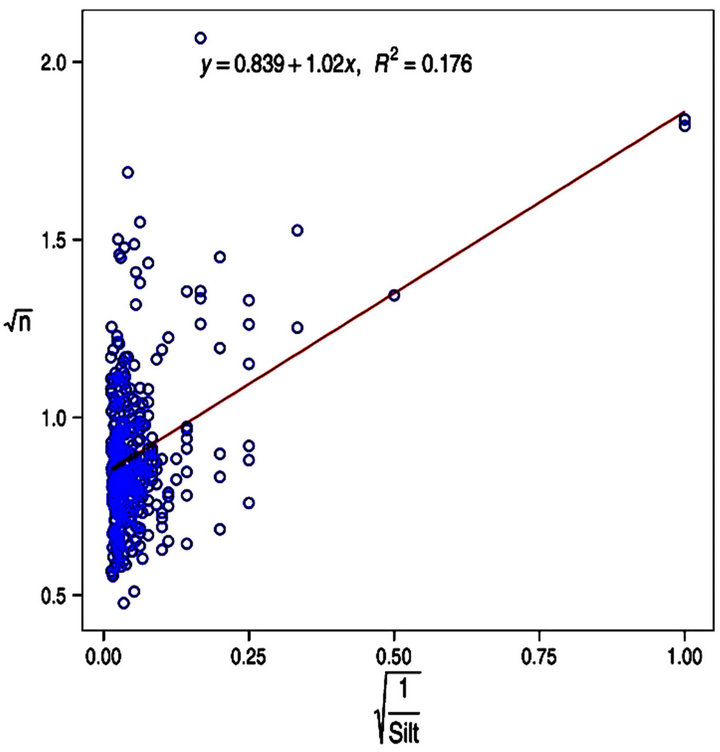 (b)
(b)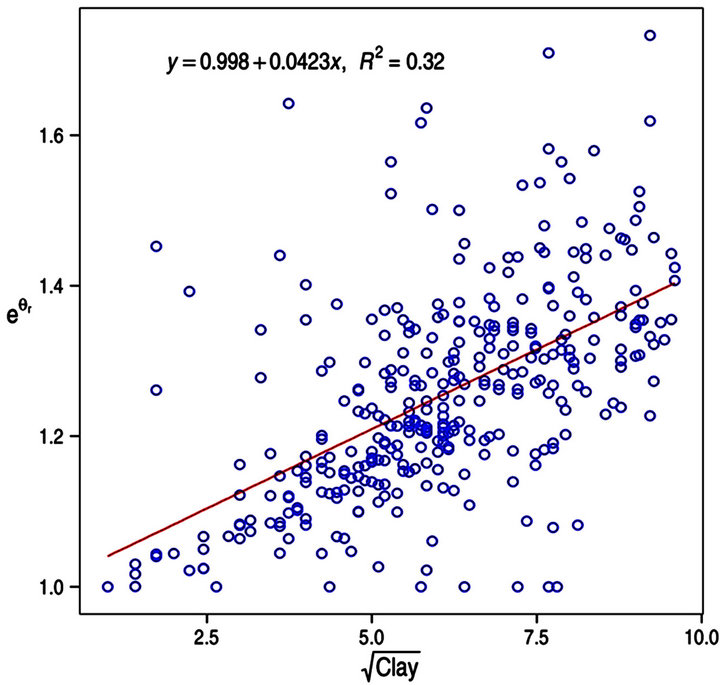 (c)
(c) (d)
(d)
Figure 3. Response versus predictor variables correlations with corresponding best possible quality fit.
After performing linear regression between two variables involving the selected transformed response variables, associated with the moisture retention parameters, and the predictor variables associated with the basic soil properties, the following conclusions were arrived at. For the transformed response variable 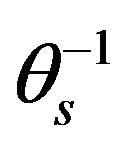 the predictor variables that yielded the best possible quality of fit with it when linear regression was performed were sand, silt−1, BD3, clay2, and ln(orgC). These variables would then be used in developing the multiple linear regression between the said response variable and the predictor variables. In the case of
the predictor variables that yielded the best possible quality of fit with it when linear regression was performed were sand, silt−1, BD3, clay2, and ln(orgC). These variables would then be used in developing the multiple linear regression between the said response variable and the predictor variables. In the case of , the best possible fit (measured by the value of R2) was obtained from linear regression with sand, silt10, BD2,
, the best possible fit (measured by the value of R2) was obtained from linear regression with sand, silt10, BD2, 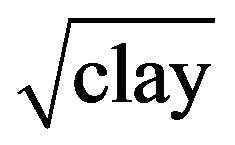 , and ln(orgC), while in the case of
, and ln(orgC), while in the case of 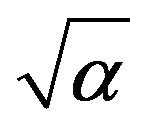 the best possible fits were obtained with esand , Silt−1, BD, Clay−1, and ln(orgC). In the case of
the best possible fits were obtained with esand , Silt−1, BD, Clay−1, and ln(orgC). In the case of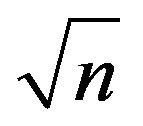 , the best possible quality of fit was obtained with the predictor variables Sand5, silt−1, ln(clay), (orgC2)−1.
, the best possible quality of fit was obtained with the predictor variables Sand5, silt−1, ln(clay), (orgC2)−1.
3.3. Multiple Regression Analysis and Accuracy of the Pedotransfer Functions Developed
Table 3 shows the quality of fit obtained when multiple linear regression was performed between each selected response variable and the transformed predictor variables to which it relates best e.g. a multiple linear regression performed between the response variable 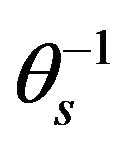 and sand, silt−1, BD3, clay2, ln(orgC), yielded the quality of fit meas ured by R2 = 0.63 which is considered acceptable and therefore accurate. The resulting equation is illustrated below Equation (12). The predictor variables indicated above that related best in linear regression with the selected response variables were the ones considered in developing the pedotransfer functions using multiple linear regression.
and sand, silt−1, BD3, clay2, ln(orgC), yielded the quality of fit meas ured by R2 = 0.63 which is considered acceptable and therefore accurate. The resulting equation is illustrated below Equation (12). The predictor variables indicated above that related best in linear regression with the selected response variables were the ones considered in developing the pedotransfer functions using multiple linear regression.
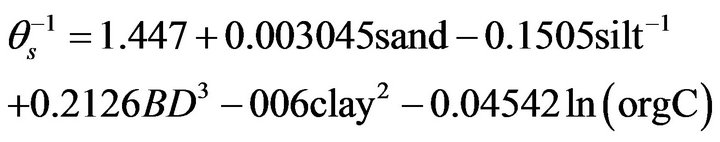 (12)
(12)
where θs is the saturated soil moisture content (cm3/cm3), silt the % silt, sand the % sand, BD the bulk density (g/cm3), clay the % clay, and orgC the Organic carbon content (g/kg). The qualities of fit for the remaining transformed response variables are illustrated in Table 3 for each of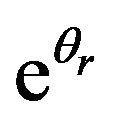 ,
, 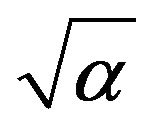 and
and 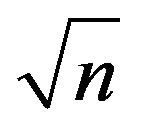 when the simple linear regression was done with the selected predictor variable transformations.
when the simple linear regression was done with the selected predictor variable transformations.
3.4. Analysis of Cross Correlation and Correlation Matrix
Cross correlation was done for the independent variables (transformations) used in developing multiple linear regression for each of the response variables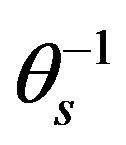 ,
,  ,
, 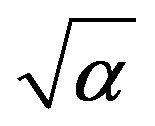 and
and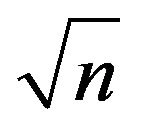 . Tables A1-A4 (Appendix) shows the relationships, based on correlation coefficient, between the various predictor variables used for each of the response variable transformations. In the case of
. Tables A1-A4 (Appendix) shows the relationships, based on correlation coefficient, between the various predictor variables used for each of the response variable transformations. In the case of 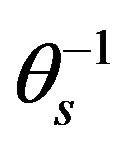 the predictor variables sand and
the predictor variables sand and 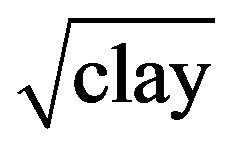 appear to be highly negatively correlated with r = −0.71 while BD3 and ln(orgC) are also fairly correlated in a negative sense (r = −0.59). For the dependent variable
appear to be highly negatively correlated with r = −0.71 while BD3 and ln(orgC) are also fairly correlated in a negative sense (r = −0.59). For the dependent variable , the response variables BD3 and ln(orgC) are also closely correlated in the negative sense with r = −0.62. Other reasonable correlations include that between esand and silt−2 (r = 0.89), BD and ln(orgC) (r = −0.64) in the case of predictor variables for
, the response variables BD3 and ln(orgC) are also closely correlated in the negative sense with r = −0.62. Other reasonable correlations include that between esand and silt−2 (r = 0.89), BD and ln(orgC) (r = −0.64) in the case of predictor variables for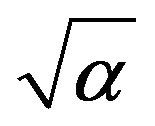 . The other significant correlations observed is that between sand5 to (silt)−1 (r = 0.74) and sand5 to ln(Clay) (r = −0.69) in the predictor variables for
. The other significant correlations observed is that between sand5 to (silt)−1 (r = 0.74) and sand5 to ln(Clay) (r = −0.69) in the predictor variables for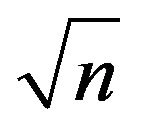 .
.
3.5. Multiple Linear Regression Results
For each of the selected response variables, Table 3 shows the various possible combinations of the predictor variables that were used in performing the multiple linear regression and also indicates the qualities of fit obtained based on the coefficient of determination R2.
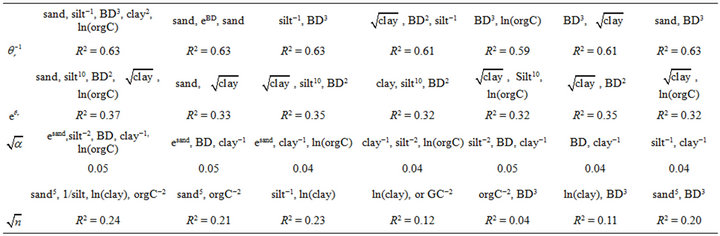
Table 3. Measurement of Quality of fit based on coefficient of determination (R2) between the moisture retention parameters (response variables) and selected predictor variable transformations in the multiple linear regression.
The various possible multiple linear regression equations obtained for the various independent variables are underlisted (Equations (13)-(27)). The choice of the independent variables or their transformations was based on combinations that would yield the highest possible quality of fit i.e. the predictor variable combinations chosen include the variable that relate very well with the response variable, hence the equations are the best possible equations that could be obtained using the variables indicated. Equations developed involving 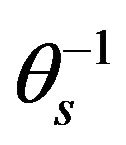 are as follows with the measures of accuracy based on coefficient of determination (R2) indicated:
are as follows with the measures of accuracy based on coefficient of determination (R2) indicated:
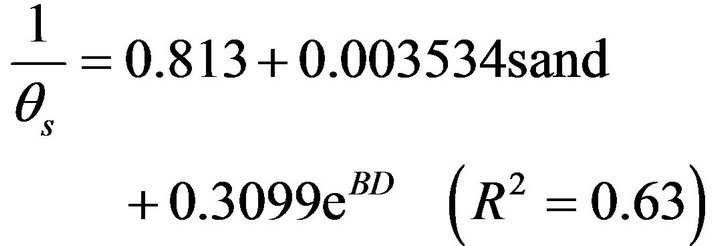 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
The set of possible multiple linear regression equations developed involving 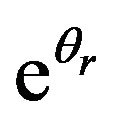 are listed as follows:
are listed as follows:
 (17)
(17)
 (18)
(18)
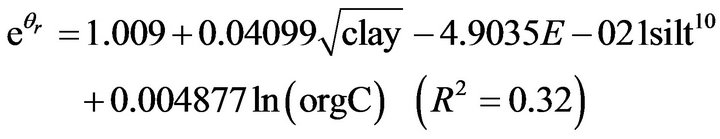 (19)
(19)
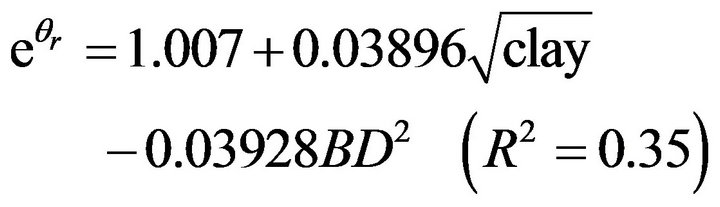 (20)
(20)
The set of possible multiple linear regression equations developed involving 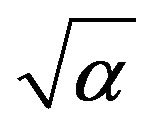 are listed as follows:
are listed as follows:
 (21)
(21)
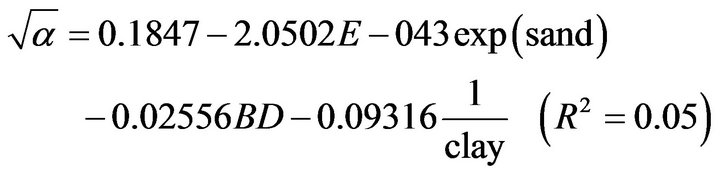 (22)
(22)
 (23)
(23)
The set of possible multiple linear regression equations developed involving  are listed as follows:
are listed as follows:
 (24)
(24)
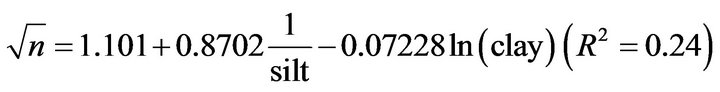 (25)
(25)
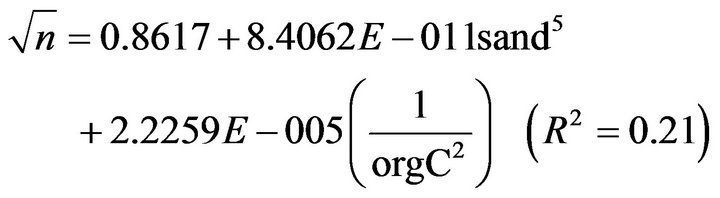 (26)
(26)
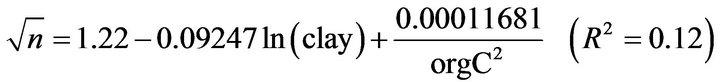 (27)
(27)
Based on the above indicated equations that produced the best quality of fit, equations relating the moisture retention parameters that are not transformed to the trans
formed basic properties were also compared to the measured (fitted) parameters and yielded the values of R2 indicated (Equations (28) to (31)) alongside the equations.
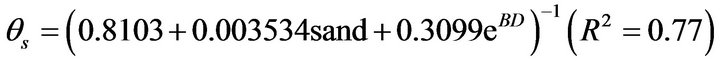 (28)
(28)
3.6. Validation of the Developed Pedotransfer Functions to Evaluate Reliability
Table 4 shows regression equations developed for each of
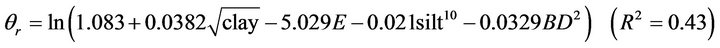 (29)
(29)
 (30)
(30)
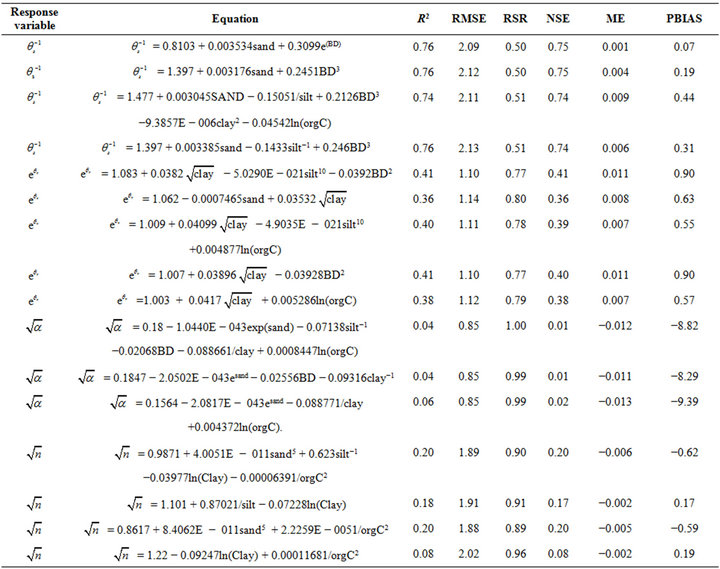
Table 4. Summary of equations for transformations of van Genuchten parameters and their performance in reliability.
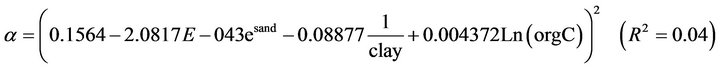 (31)
(31)
the selected transformations of the moisture retention parameters of the van Genutchen moisture retention equation and measures of their performance in validation based on the statistical measures indicated. The transformed model parameter that yielded the best reliability is the saturated soil moisture content 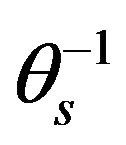 (considering the measure of coefficient of determination (R2 = 0.76). This indicates that θs is reasonably well predicted by the pedotransfer function developed. Prediction of transformed variable
(considering the measure of coefficient of determination (R2 = 0.76). This indicates that θs is reasonably well predicted by the pedotransfer function developed. Prediction of transformed variable  yielded the lowest possible value for the selected measure for the quality of fit (r = 0.25) reflecting the lowest level of reliability compared to the other pedotransfer functions developed for moisture retention parameters under consideration.The transformed variable for residual moisture content
yielded the lowest possible value for the selected measure for the quality of fit (r = 0.25) reflecting the lowest level of reliability compared to the other pedotransfer functions developed for moisture retention parameters under consideration.The transformed variable for residual moisture content  yielded modest performance with the best possible value of R2 = 0.41.
yielded modest performance with the best possible value of R2 = 0.41.
[4] notes that continuous pedotransfer functions can be applied in the case of more site specific applications, where measured data is available, since they do not provide site specific information. The pedotransfer functions predict soil hydraulic characteristics for broadly defined textural classes. Figures 4-7 illustrates the performance of the developed pedotransfer functions for the transformed response variables based on analysis by linear regression.
4. Conclusion and Recommendation
The performance of developed pedotransfer functions for estimating moisture retention parameters in the van Genuchten moisture retention equation varied for the individual moisture retention parameters. Equations deve-
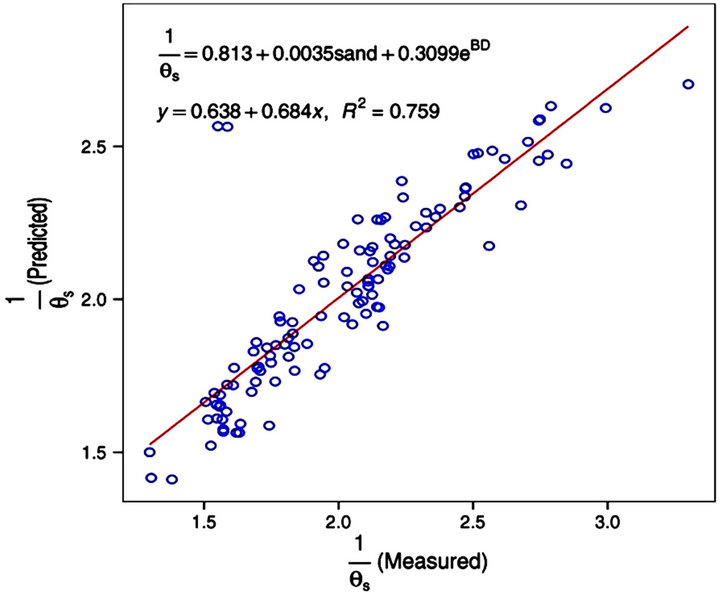
Figure 4. Predicted value of transformed variable 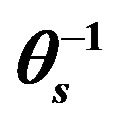 versus measured by correlation for a developed equation that yielded the best possible quality of fit.
versus measured by correlation for a developed equation that yielded the best possible quality of fit.

Figure 5. Predicted value of transformed variable  versus measured by correlation for a developed equation that yielded the best possible quality of fit.
versus measured by correlation for a developed equation that yielded the best possible quality of fit.
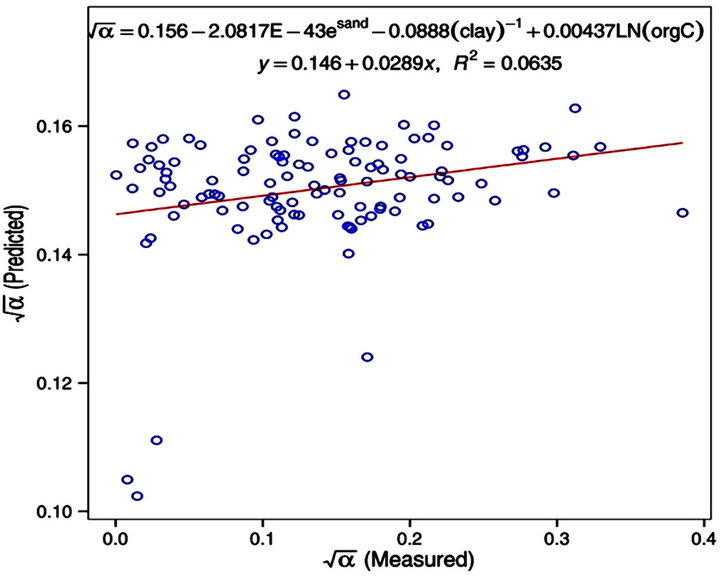
Figure 6. Predicted value of transformed variable 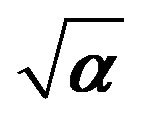 versus measured by correlation for a developed equation that yielded the best possible quality of fit.
versus measured by correlation for a developed equation that yielded the best possible quality of fit.
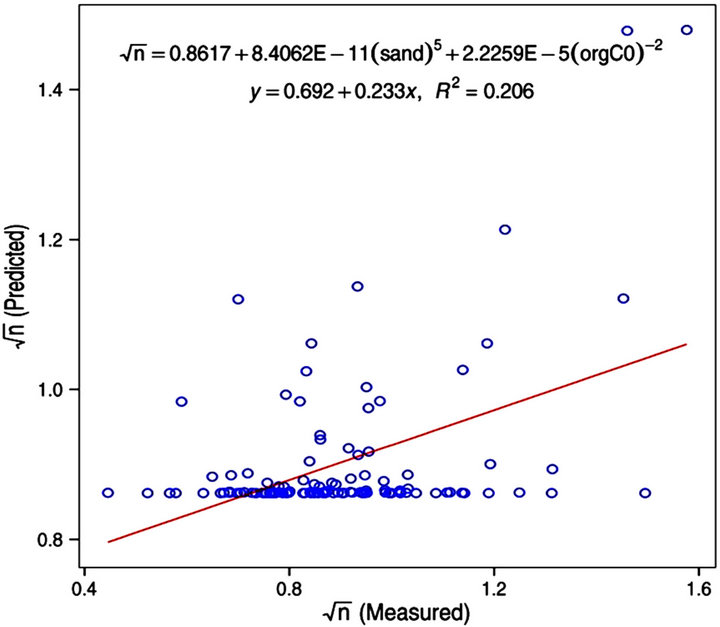
Figure 7. Predicted value of transformed variable 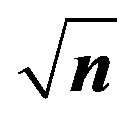 versus measured by correlation for a developed equation that yielded the best possible quality of fit.
versus measured by correlation for a developed equation that yielded the best possible quality of fit.
loped for predicting saturated soil moisture content (θs) yielded the best performance in model validation with the highest possible value of coefficient of determination R2 = 0.76, RMSE = 2.09 and a NSE of 0.75. The relatively poorest performance was observed with the parameter “α” with the best possible value of R2 being 0.06 indicating unsatisfactory performance and a RMSE value of 0.85. The remaining parameters (θr and “n”) registered performance intermediate between the aforementioned two extremes. It is therefore evidently not possible to obtain excellent performance in pedotransfer functions for all the parameters. The equations derived from these parameters would be the best possible obtainable for estimating hydraulic conductivity. Continued effort should be made in developing more pedotransfer functions to provide users with more alternative equations and especially those PTFs that use the very basic soil properties available in many local soils data bases.
5. Acknowledgements
I wish to acknowledge the support provided by the Deans Committee Research Grant, University of Nairobi (UoN) who funded the research project, The Principal’s office College of Architecture and Engineering (UoN) who funded journal publication fees. I also wish to acknowledge support given by staff of the department of Environmental and Biosystems Engineering (UoN) who contributed useful academic ideas that enriched this document.
REFERENCES
- H. R. Fooladmad, “Pedotransfer Functions for Point Estimation of Soil Moisture Characteristic Curve in Some Iranian Soils,” African Journal of Agricultural Research, Vol. 6, No. 6, 2011, pp. 1586-1591.
- J. P. O. Obiero, “Evaluation of Infiltration Using Green Ampt Model and Rainfall Runoff Data for Lagan and Sambret Catchments, Kericho, Kenya,” M.Sc. Thesis, Department of Agricultural Engineering, University of Nairobi, Nairobi, 1996.
- A. Rasoulzadeh, “Estimating Hydraulic Conductivity Using Pedotransfer Functions,” In: L. Elango, Ed., Hydraulic Conductivity Issues, Determination, and Applications, Intech, 2011, pp. 145-164. doi:10.5772/22753
- K. E. Saxton and W. J. Rawls, “Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions,” Soil Science Society of America Journal, Vol. 70, No. 5, 2006, pp. 1569-1578.
- M. G. Schaap and F. J. Leij, “Using Neural Networks to Predict Soil Water Retention and Soil Hydraulic Conductivity,” Soil and Tillage Research, Vol. 47, No. 1-2, 1998, pp. 37-42. doi:10.1016/S0167-1987(98)00070-1
- J. Tomasella and M. Hodnett, “Pedotransfer Functions in Tropical Soils,” In: Y. Pachepsky and W. J. Rawls, Eds., Development of Pedotransfer Functions in Soil Hydrology. Developments in Soil Science, Vol. 30, Elsevier B. V., Amsterdam, 2004, pp. 415-429.
- H. Vereecken and M. Herbst, “Statistical Regression,” In: Y. Pachepsky and W. J. Rawls, Eds., Development of Pedotransfer Functions in Soil Hydrology. Developments in Soil Science, Vol. 30, Elsevier B. V., Amsterdam, 2004, pp. 3-19.
- R. T. Walczack, F. Moreno, C. Slawinski, E. Fernandez and J. L. Arrue, “Modelling of Soil Water Retention Curve Using Soil Solid Phase Parameters,” Journal of Hydrology, Vol. 329, No. 3-4, 2006, pp. 527-533. doi:10.1016/j.jhydrol.2006.03.005
- T. Wells, S. Fityus, D. W. Smith and H. Moe, “The Indirect Estimation of Saturated Hydraulic Conductivity of Soils, Using Measurements of Gas Permeability. I. Laboratory Testing with Dry Granular Soils,” Australian Journal of Soil Research, CSIRO Publishing, 2006. http://www.highbeam.com
- J. H. Wosten, M. Y. A. Pachepsky and W. J. Rawls, “Pedotransfer Functions: Bridging the Gap between Available Basic Soil Data and Missing Soil Hydraulic Characteristics,” Journal of Hydrology, Vol. 251, No. 3-4, 2001, pp. 123-150. doi:10.1016/S0022-1694(01)00464-4
- N. H. Batjes, Ed., “A Homogenized Soil Data File for Global Environmental Research: A Subset of FAO, ISRIC, and NRCS Profiles (Version 1.0),” Working Paper and Preprint 95/10b, International Soil Reference and Information Centre, Wageningen, 1995. http://www.isric.org/NR/exeres/545B0669-6743-402B-B79A-DBF57E9FA67F.htm
- M. van Genutchen, “A Closed Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils,” Soil Science Society of America Journal, Vol. 44, No. 5, 1980, pp. 892-898. doi:10.2136/sssaj1980.03615995004400050002x
Appendix
Analysis of Cross Correlations

Table A1. Cross correlation tests for transformed predictor variables for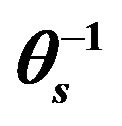 .
.

Table A2. Cross correlation tests for transformed predictor variables in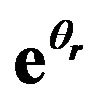 .
.

Table A3. Cross correlation tests for transformed predictor variables in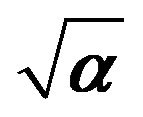 .
.

Table A4. Cross correlation tests for transformed predictor variables in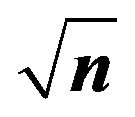 .
.

