Open Journal of Forestry
Vol.05 No.01(2015), Article ID:53384,8 pages
10.4236/ojf.2015.51007
Predicting the Growth in Tree Height for Building Sunshine in Residential District
Bo Hong
College of Landscape Architecture and Arts, Northwest A&F University, Yangling, China
Email: hongbo@nwsuaf.edu.cn
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 December 2014; accepted 12 January 2015; published 20 January 2015
ABSTRACT
Residential greening constitutes a significant portion of the urban environment. Trees, as the largest entities in the tree-shrub-herb greening system, are the best choice for residential afforestation. Hence, tree arrangement in green space between buildings is significant, for which may exert negative impact on building sunshine. This study takes He Qingyuan residential area in Beijing as a case study to predict the growth in tree height between buildings to meet good sunshine requirements. The procedures were draw as follows: 1) models including building layout and trees were built using computer-aided design (Auto CAD). Afterwards, according to tree crown shape, tree height limits were determined for the same building layout; 2) and after that, the growth in tree height was predicted using the nonlinear height-diameter functions to meet the good sunshine requirements. The results allow us to determine which trees to plant between buildings in that the designers can predict the effects of future tree growth on building sunshine.
Keywords:
Tree Height, Building Sunshine, Residential District, Computer-Aided Design, Nonlinear Height-Diameter Function

1. Introduction
Trees in residential areas carry out a number of important functions. They reduce energy use by shading building during the summer and reducing wind speeds during the winter. If planted in large numbers, trees can cool the summer climate of an entire metropolitan area, helping to mitigate the urban heat island effect (Frelich, 1992) . Trees can also use large quantities of CO2 to make wood, which helps retard the buildup of this greenhouse gas in the atmosphere (Akbari, 2002) . Despite the importance of trees in residential areas, if planted improperly, the trees would bring about negative impact on residents’ daily life, for example, evergreen trees such as Photinia serrulata (Chinese Photinia), which were planted too near a building, there is almost no sunshine all the day in winter, and large trees such as Cedrus deodara (India Cedar), can affect the daylight of fourth or higher floor, which results in decreasing functions of eradicating bacteria, reducing indoor humidity and increasing indoor temperature in winter (Yuan, 2009) . On the contrary, sufficient sunshine has the function of maintaining a healthy indoor environment and reducing energy consumption when compared with mechanical cooling system (Balocco, 2011) .
While the growth of trees is a dynamic process, and available information on dimensional relationships of commonly trees is usually made empirically from the varying standpoints of conventional planning concepts or landscape design, and the observations are based on perceptions of rates at trees grow (Kirsten & Meyer, 1992) . Subjective terms such as slow, moderate, quick or fast are used to describe tree growth without these terms being substantiated with quantitative values. Qualitative growth information on residential trees that are suitable for urban greening is exceptionally limited, so landscape architectural designers often meet dilemma when planting trees in green space between buildings (GSBB).
Tree height-diameter relationship is an important component in yield estimation, growth and landscape appraisal (Parresol, 1992) . Curtis summarized a large number of available height-diameter functions and used Furnival’s index of fit to compare the performance of 13 linear functions fitted to second-growth Pseudotsuga menziesii (Mirb.) Franco data (Curtis, 1967) . Since then, many height-diameter equations have been developed for various tree species. Among a variety of mathematical equations, nonlinear height-diameter functions have now been widely used in height predictions (Schreuder et al., 1979) .
The aim of the research presented here was therefore to determine the relationships between tree height and age using nonlinear height-diameter function for trees commonly used in residential greening and to use this relationship to predict tree growth, and then, analyze whether the growth of trees height would have affect on building sunshine. In contrast, the results presented here may be used to model dimensional growth of tree species with statistical methods.
2. Methodology
2.1. Research Method
Figure 1 shows the schematic flow of the system for predicting the growth in tree height for building sunshine. Firstly, site measurements were carried out, including the height of tees and the crown diameter of trees; Secondly, trees were classified into the selected four common typical tree configurations, and further calculated maximum tree height in green space between buildings (GSBB) with serious of equations; Thirdly, with the nonlinear height-diameter function to predict the tree growth, and to analyze whether the growth of tree would affect the building sunshine.
2.2. Site Measurement
The trees in He Qingyuan residential district were measured in the early spring of 2011. The tree height, the crown diameter and crown base height (height from the ground to the lowest leaves of the crown) were measured with a graduated 3 m range pole. According to the crown dimension, all the trees without partial crown
Figure 1. Schematic flow of the system.
were classified into five categories in landscape planting design: cylindrical, conical, spherical, inverted conical and umbrella-shaped trees (Li, 2010) . Therefore, the crown of umbrella-shaped trees is irregular and asymmetrical, and this type of trees is uncommon in Beijing area, so the crown of umbrella-shaped trees is excluded in this study. So the author selected four common typical tree configurations (Table 1, Figure 2), and then trees in residential district were classified into the four configurations (Table 2).
The measured trees were planted in 2002 and the planting dates refer to the date refer to the date at which the trees were physically planted in the residential district. The original tree dimensions were obtained from the landscape architectural planting design map. Trees ages are taken in years since they were planted in the residential district, due to certain instances of uncertainty of the age of the saplings when planted in the residential district.
The majority of the measured trees grew in irrigated, managed lawn residential environment, and the trees were all planted in green space between buildings (GSBB). The tree height was regressed on age to compute the growth rate of each dimension for each species. In a study to analyze the stem circumference growth, several growth curve models were tested (Stoffberg, 2006) . However, the logarithmic equation was considered to provide the most appropriate fit to stem circumference versus age data (Peper et al., 2001a) , and was therefore used to determine the dimensional growth rates for the individual species in the present study, in which age was used as independent variable and the tree height was modeled using the following equation:
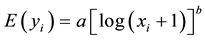 (1)
(1)
where yi is the observed response for the ith tree,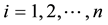 ; xi is the age of the ith tree; a, b are the parameters
; xi is the age of the ith tree; a, b are the parameters
CYLINDRICAL CONICAL SPHERICAL INVERED CONICAL
Figure 2. Four typical tree configurations in He Qingyuan district.
Table 1. Tree classification in He Qingyuan district.
aD/H is the ratio of crown diameter to tree height; PMCD is the point of the maximum crown diameter.
Table 2. Trees classified according to the tree crown shape.
to be estimated; E() is the expected value; and log is logarithm.
2.3. Computer Simulation
The pattern and layout of status building and green space of He Qingyuan district are shown in Figure 3, and four conditions and assumption were considered in this research: 1) the first-floor window, which is 0.9 m above the ground, is taken as the standard lighting point; 2) there was assumed to be effective sunshine for first-floor households from 11:00 to 13:00 on the winter solstice; 3) small-crown trees and shrubs such as flowering peach were not included in this study because they produced less impact on the sunshine of buildings; 4) tree crown was healthy and symmetrical, or at least north-south symmetrical.
As the tree shadow is determined by the seasonal changes in the solar elevation angle and horizontal shadow length rate, these factors are the basis for calculating the maximum tree height to meet low level sunshine. On the winter solstice day, the solar elevation is the lowest, evergreen trees have significant impact on sunshine, especially the first and the second floor. Therefore, the winter solstice day is generally considered to determine the height limit of evergreen trees. The autumnal equinox is the main day of defoliation of deciduous trees. Deciduous trees are considered more attractive when hold their leaves, but when the defoliation starts, they have little impact on sunshine.
The winter solstice has often been used to determine the minimum sunshine of building, and evergreen trees have a year-round effect on sunshine, the winter solstice is selected to determine the height limit of evergreen trees. As deciduous trees may have no impact on sunshine when defoliated, the autumnal equinox is used to determine the height limit of deciduous trees.
Considering the path of sunshine and a vertical pole, the co-efficient of daylighting distance was obtained by the follow equation:
 (2)
(2)
where d is the daylighting distance, h is the height of the pole, α is the local solar altitude, and β is the local solar azimuth angle.
As shown by the model in Figure 4, when building height and sunshine spacing were quantitatively obtained, the main factors that affect building sunshine were including crown, height and location of the trees. And relation of tree height and crown diameter differed for different tree species (Peper et al., 2001b) . So tree height acted as one representative indicator in tree species selection.
If a tree met the sunshine requirement with maximum tree height permitted, a few qualitative results could be drawn:
 (3)
(3)
 (4)
(4)
where dx is the distance (m) between a tree trunk and the northern building; d is the sunshine spacing; φ is the diameter of symmetrical crown (m); dy is the distance between the crown margin and southern building façade, hx is the height (m) relative to dx; hi is the tree height limit (m); 0.9 m is the height from the ground level to the
Figure 3. Photograph of GSBB in He Qingyuan district.
windowsill of the first floor.
Combining Equations (3) and (4) with (2), the relationship between tree height and sunshine spacing was:
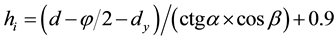 (5)
(5)
According to the research (Stoffberg, 2008) , μ was defined as the ratio of tree diameter to tree height, and represented by the following equation:
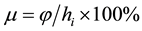 (6)
(6)
Combining Equations (2)-(4), the following equation could be obtained:
 (7)
(7)
For He Qingyuan district, the values of α, β are given in the following Table 3:
The values of α, β (Table 3) were substituted into Formula (5), α value on winter solstice day for evergreen tree, and α value on autumn equinox for deciduous tree. By numerical statement of marking the status trees in He Qingyuan, was obtained that d = 31.2 m and dy = 1.5 m. In accordance with the tree crown classification above, we could obtain μ representing different crown shapes, which was further used to figure out the maximum tree height (Table 4, Figure 5).
Figure 4. Model of one permitted highest tree between building in He Qing- yuan District. Note: in the model, dx is the distance (m) between a tree trunk and the northern building; d is the sunshine spacing; φ is the symmetrical crown diameter (m); dy is the distance between the crown margin and southern building façade; hx is the height (m) relative to dx; hi is the tree height limit (m); 0.9 m is the height from the ground level to the windowsill of the first floor.
Table 3. Solar altitude angle and solar azimuth for He Qingyuan District.
Table 4. Maximum tree height in He Qingyuan district.


Figure 5. Four types of maximum tree body configuration for the same building separation in He Qingyuan district. Note: Non-filled trees are deciduous and filled trees are evergreen; (a)-(d) largest height of tree that can be planted.
3. Results and Discussion
The relationship between age and tree height measurement could be suitably expressed by the logarithmic function and the equations derived for species used to predict tree height and growth rate at different ages. In all investigated species tree height is highest in the young trees and decrease with tree ages, although the rate of decrease differs among the species and among the growth parameter.
In contrast, the mean annual tree heights of evergreen trees increments are less than that of the mean annual tree height increments of deciduous trees. For the deciduous trees, the height of Paulownia and Locust grow faster than others, but it has been reported that certain trees of these species only have reached an age of less than 25 years in Beijing. The regression equations presented are only valid with the sample range of ages before 25 years and exploration beyond these ranges are therefore not recommended (Table 5).
From 1 to 20 years, the growth height of Gingko increased fast, while tended to slow growth after the 50 years. Similarity, the tree height of Purple blow maple increased faster from 1 to 30 years (Figure 6). In the whole life span of Gingko and Purple blow maple in He Qingyuan residential district, they could not reach the maximum tree height, and thus would not affect the building sunshine. The tree height of Spruce, White bark pine and Chinese pine increase slower than Juniper, and the height tend to increase slight after 30 years (Figure 7). While the tree height of Juniper increase to 14.1 m in 30 years, although the speed of growth of tree height increase slightly after 30 years, it would influence the building sunshine when reach the ages of 30, according the permitted maximum tree height mentioned above. Paulownia keeps a faster increasing speed of tree height growth from 1 to 20 years, and the tree height reaches almost 26.5 m at the age of 18 years, which would exceed the permitted maximum height of tree for building sunshine.
The height of Tree of heaven and Golden rain tree increase faster from 1 to 30 years, while Chinese wax and Gold-rimmed weeping from 1 to 15 years (Figure 8), but the increasing speed tend to change slow after 30 years. In the life span of these four deciduous trees, the tree height would not reach the maximum tree height. The tree height of Locust keeps a high increasing, and the height reaches 26.4 m after planted 22 years, which exceed the permitted maximum tree height (Figure 9). While the rapid tree growth of Silk tree concentrated in the period from 1 to 15 year, and tend to increase slower after 20 years.
4. Conclusion and Prospect
This study described the growth of tree height in residential area from 1 to 30 years, further analyzed the impact
Figure 6. Predicted height by age for cylindrical trees.
Figure 7. Predicted height by age for conical trees.
Figure 8. Predicted height by age for spherical trees.
of trees on building sunshine during the growth, with primary emphasis on the younger years because that was when planners traditionally attempt to forecast their growth. The conclusions could be drawn as follows.
1) There is a rapid decline in the tree height growth rate with age. Moreover, most of the tree height increase faster concentrated in the period from 1 to 15 years, and the mean annual tree heights of evergreen trees
Figure 9. Predicted height by age for inverted conical trees.
Table 5. Predicted tree height of the tree species at 10, 15 and 30 years after planting.
increments are less than that of the mean annual tree height increments of deciduous trees.
2) In comparison, trees like Gingko, Silk tree and most of the evergreen conifers were better suited to be used in landscape projects where space was restricted and where a slow growth rate was desired. Locust and Paulownia, on the other hand, were suitable for large open spaces and for landscape where fast tree growth rates are required. This is because tree species tends to become very large and may be inappropriate for such small spaces.
3) Many studies have shown that the average life span of urban trees is very short and can be as low as 10 to 15 years (Foster & Blaine, 1978) . This study shows that within the actual life span of urban trees, it will be difficult to obtain the permitted maximum tree height, so it can be concluded that the trees planted in the green space between buildings (GSBB) will not affect the building sunshine in He Qignyuan district.
The purpose of this study is to make it possible at any given time to forecast the dimensions of the trees as functions of age. It should be possible to use this function to estimate the consequences of planting grids, and in landscape design, to provide the landscape designer with quantitatively derived tree age to tree dimension relationship, which will provide more realistic landscape architectural plans, elevations and perspectives. With this function, applications for dynamic illustrations can be made more realistically in urban environments using tools such as Auto CAD, tree growth can then be digitally simulated. When presenting the quantitatively derived CAD simulations, the tree growth can be viewed in context of the designed landscape and related architecture. This can result in simulating how the landscape will change over time as the trees increase in age. The visual presentation will allow both architects and clients a more realistic dynamic simulation of their investment. They are also used in a landscape architectural context to derive spatial and aesthetic functions (Flemming & Palle, 2002) .
This article discusses the effect of age-height relationship on sunshine, therefore, other parameters of the tree, such as tree crown diameter and diameter of breast height, also grows with the tree height increase, while these information relating to tree height and crown height dimensions can be applied to model air pollution uptake, microclimate amelioration, carbon sequestration and rainfall interception in urban environments (Xiao & McPherson, 2002) . This information on tree also enables the calculation of the growth of tree height and tree crown dimensions and their relationships, which permit urban foresters to calculate, amongst others, the costs and benefits of the urban forest (Mcpherson et al., 2011) .
Acknowledgements
The research work was supported by the Special Fund Project of Basic Scientific Research of Northwest A&F University (Grant No.2014YB076).
References
- Akbari, H. (2002). Shade Trees Reduce Building Energy Use and CO2 Emissions from Power Plants. Environmental Pollution, 116, 119-126. http://dx.doi.org/10.1016/S0269-7491(01)00264-0
- Balocco, C. (2011). Hospital Ventilation Simulation for the Study of Potential Exposure to Contaminants. Building Simulation, 4, 5-20. http://dx.doi.org/10.1007/s12273-011-0019-6
- Curtis, R. O. (1967). Height-Diameter and Height-Diameter-Age Equations for Second-Growth Douglas-Fir. Forestry Science, 13, 365-375.
- Flemming, K. L., & Palle, K. (2002). Tilia’s Physical Dimensions over Time. Journal of Arboriculture, 28, 209-213.
- Foster, R. S., & Blaine, J. (1978). Urban Tree Survival: Trees in the Side-Walk. Journal of Arboriculture, 4, 14-17.
- Frelich, L. E. (1992). Predicting Dimensional Relationship for Twin Cites Shade Trees. St. Paul, MN: Department of Forest Resources, University of Minnesota, 1-33.
- Kirsten, K. E., & Meyer, L. (1992). Keith Kirsten’s Complete Garden Manual for South Africa. Cape Town: Human and Rousseau.
- Li, S. H. (2010). Landscape Planting Design. Beijing: China Agriculture Press.
- Mcpherson, E. G., Simpson, J. R., Xiao, Q. F., & Wu, C. X. (2011). Million Trees Los Angeles Canopy Cover and Benefit Assessment. Landscape and Urban Planning, 99, 40-50. http://dx.doi.org/10.1016/j.landurbplan.2010.08.011
- Parresol, B. R. (1992). Bald Cypress Height-Diameter Equations and Their Prediction Confidence Intervals. Canadian Journal of Forest Research, 22, 1429-1434. http://dx.doi.org/10.1139/x92-191
- Peper, P. J., Mcpherson, E. G., & Mori S. M. (2001a). Equations for Predicting Diameter, Height, Crown Width, and Leaf Area of San Joaquin Valley Street Trees. Journal of Arboriculture, 27, 306-317.
- Peper, P. J., Mcpherson, E. G., & Mori S. M. (2001b). Predictive Equations for Dimensions and Leaf Area of Coastal Southern California Street Trees. Journal of Arboriculture, 27, 169-181.
- Schreuder, H. T., Hafley, W. L., & Bennett, F. A. (1979). Yield Prediction for Unthinned Natural Slash Pine Stands. Forestry Science, 25, 25-30.
- Stoffberg, G. H. (2006). Growth and Carbon Sequestration of Street Trees in the City of Tshwane, South Africa. Ph.D. Thesis, Pretoria: University of Pretoria.
- Stoffberg, G. H., Van Rooyen, M. W., Van Der Linde, M. J., & Groeneveld, H. T. (2008). Predicting the Growth in Tree Height and Crown Size of Three Street Tree Species in the City of Tshwane, South Africa. Urban Forestry & Urban Greening, 7, 259-264. http://dx.doi.org/10.1016/j.ufug.2008.05.002
- Xiao, Q. F., & McPherson, E. G. (2002). Rainfall Interception by Santa Monica’s Municipal Urban Forest. Urban Ecosystems, 6, 291-302. http://dx.doi.org/10.1023/B:UECO.0000004828.05143.67
- Yuan, B. C. (2009). Research on Health-Based Residential Building Sunshine. Foreign Medical Sciences (Section Hygiene), 36, 23-28.













