Advances in Physical Education
Vol.4 No.2(2014), Article ID:45900,9 pages DOI:10.4236/ape.2014.42013
Interpersonal Angular Relations between Players Constrain Decision-Making on the Passing Velocity in Futsal
Umberto Cesar Corrêa1, Luis Vilar2,3, Keith Davids4, Ian Renshaw5
1School of Physical Education and Sport, University of Sao Paulo, Sao Paulo, Brazil
2Faculty of Human Kinetics, Technical University of Lisbon, Lisbon, Portugal
3Faculty of Physical Education and Sports, Lusophone University of Humanities and Technologies, Lisbon, Portugal
4Centre for Sports EngineeringResearch, Sheffield HallamUniversity, Sheffield, UK
5School of Exercise and Nutrition Science, Queensland University of Technology, Brisbane, Australia
Email: umbertoc@usp.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 March 2014; revised 9 April 2014; accepted 16 April 2014
ABSTRACT
The aim of this study was to investigate the influence of interpersonal interactions between players on the regulation of ball passing velocity in the team sport of futsal. For this purpose 28 sequences of play, in which passes were performed between outfield players, were selected from an elite futsal competition and analyzed using TACTO software. Relative angles between attackers and defenders were used to examine interpersonal coordination tendencies that emerged during performance. Results showed that ball passing velocity was constrained by the rate of change of the angle created by the following vectors: “ball carrier-ball receiver” and “ball carrier-ball receiver’s nearest defender”. Passing velocity remained the same when that angular value remained within a critical threshold range between −18.16˚/s to 11.26˚/s. Beyond those critical threshold values, angular relations between participants seemed to enter into a new critical state requiring the emergence of a new passing velocity for performance success. The findings of this study allowed us to conclude that passing velocity during competitive performance in futsal was regulated by the rate of change of an angle established by the interaction between the ball carrier to ball receiver vector with the ball carrier to ball receiver’s nearest defender vector.
Keywords:Ecological Dynamic, Informational Variable, Team Sports, Motor Skill

1. Introduction
In the past decade researchers have increasingly recognized the importance of decision-making in team sports as one of the most influential processes explaining performance (Araújo, Davids, & Hristovski, 2006; Gréhaigne, Godbout, & Bouthier, 2001; Griffin & Butler, 2005; Turner & Martinek, 1995). For instance, what, when, where, and how to do in specific situations have been some of the questions often made by researchers in order to understand the players’ decision-making in team sports.
Recently, ecological dynamics has been recognized as a reliable framework for explaining decision-making processes at the level of the performer-environment relationship (i.e., at the ecological scale of analysis) (Araújo, Davids, & Hristovski, 2006; Davids, Button, Araújo, Renshaw, & Hristovski, 2006; Vilar, Araújo, Davids, & Button, 2012). A basic assumption of ecological dynamics is that the ambient energy fields (e.g., light, sound) surrounding performers are rich in information that specifies properties of the environment and which is used to regulate actions (Gibson, 1986). A functional relationship is established between the interacting constraints of the performer and the performance environment, from which opportunities for actions emerge in the shape of affordances (Araújo et al., 2006; Fajen & Turvey, 2003). These ideas suggest that performers make successful decisions by picking up and using information relevant to the physical properties of team game performance, for example interpersonal distances and relative velocities of interacting individuals (Davids & Araújo, 2010; Duarte et al., 2010a; Esteves, Oliveira, & Araújo, 2011; Passos et al., 2008).
Research has revealed that stable patterns of coordination emerge from cooperative interactions between teammates and competitive interactions with opponents during team game performance (Corrêa, Alegre, Freudenheim, Santos, & Tani, 2012a; McGarry & Franks, 1996; McGarry, Anderson, Wallace, Hughes, & Franks, 2002; McGarry, 2009). Performers are constrained by their perceptions of opportunities to act and by perceptions of opportunities for opponents to act (Richardson, Marsh, & Baron, 2007). However, constraints in team sports alter on a moment-to-moment basis, and players need to make decisions to continually adapt to changes in the performance context caused by positional changes of performers relative to other players (both teammates and opponents), the ball and the goal (Davids, 2009; Hughes, Dawkins, David & Mills, 1998).
Decision-making in team sports has been investigated by considering the information that constrains the coordination tendencies that emerge in attacker and defender dyadic systems (Araújo, Davids, Bennett, Button, & Chapman, 2004; Davids et al., 2006). The coupling between an attacker and the closest defender has been suggested to be the basic unit of analysis for studying the spatiotemporal relations between players in team game performance (McGarry et al., 2002). For example, research on such dyadic systems has shown that in rugby-union, basketball and futsal the attackers’ decisions to drive past the opponents occurred at short distances from defenders (Duarte et al., 2010a; Esteves, Oliveira, & Araújo, 2011; Passos et al., 2008). In addition, angles between attackers and defenders have been identified as potential measures of interpersonal coordination tendencies describing the structural organisation in team games which capture the relationship between individuals acting within and between dyads. For instance, recently Corrêa, Vilar, Davids, and Renshaw (2012b) investigated the influence of interpersonal angular relations on the futsal players’ decision-making about the passing direction. They found that the direction for a pass emerged from specific angles involving the ball carrier, ball receiver, and their nearest defenders; and, that the passing direction was also influenced by the velocities and variabilities of changes of the players’ angular relations. In the present study, we aimed to extend the knowledge from this previous one about where to pass by investigating the futsal players’ decision-making on how to pass (e.g. fast or slow passes).
In the team sport of futsal, the interpersonal coordination tendencies between the ball carrier, ball receiver and nearest defenders might be captured through establishing the relationship between two vectors reflecting passing and interception possibilities, respectively: 1) the vector from the ball carrier to the ball receiver; and 2) the vectors from the attackers to their immediate defenders. Analysis of the angular relationships established by the interactions of these vectors may reveal how positional information from opponents may constrain the ball carrier’s decision to pass the ball to a teammate (Corrêa et al., 2012b). Furthermore, considering recent findings that the defender’s positioning relative to the ball’s trajectory constrains the interception of a passed ball in the game of futsal (Travassos et al., 2012), results were expected to reveal, from the ball carrier perspective, how passing decision-making may be influenced by the perception of passing and interception possibilities, afforded by the interacting vectors.
In this sense, the aim of this study was to examine how the angular relationships established between individuals in dyads constrained the ball carrier’s decisions in applying specific velocity values to the displacement of a ball when attempting to pass it to a teammate. We sought to examine how the angular relationship between the attackers and defenders position and the ball trajectory of a pass influenced the velocity of the ball needed to successfully reach a teammate.
2. Method
This study was conducted within the guidelines of the American Psychological Association and the protocol received approval from a local university ethics committee.
2.1. Data Collection
From those sequences of play in which the pass was performed along the ground a random selection was considered. Twenty-eight sequences of play (M = 1.57, SD = 1.02 seconds of duration) in which passes were performed between outfield players of both teams were selected from the final of the UEFA Futsal Cup 2010 held in Lisbon. 24 male professional players (M = 30.04, SD = 4.10 years of age) participated in this game. This game was recorded using a digital camera (Sony DCRDVD306) located above and behind the short axis of a futsal court at a frequency of 25 Hz.
2.2. Data Analysis
Each sequence of play involved the collection of data on the movement displacements of four outfield players from the moment a ball carrier received the ball until a teammate received the ball (after a pass had been performed). TACTO software was used to convert participants’ movement displacement trajectories into virtual coordinates (i.e., in pixels) (Fernandes, Folgado, Duarte, & Malta, 2010). Then, the movement displacement trajectories of the four key outfield players characterized by the following dyadic subsystems were digitized: 1) Ball carrier dyad—ball carrier and the nearest defender; 2) Ball receiver dyad—ball receiver and the nearest defender. This procedure consisted of following with a computer mouse in a slow motion video image (frequency of 2Hz), each player’s vertical projection of the working point on the floor (frequently between his feet). Then, the virtual coordinates (i.e., in pixels) were transformed into real coordinates (i.e., in meters) using a bidimensional direct linear transformation method (2D-DLT) filtered with a low pass filter (6 Hz) (Winter, 2005). This method considers the z-coordinates to be equal to zero and directly correlates an object point located in the object space/plane and a corresponding image point on the image plane (Duarte et al., 2010b; Fernandes, Folgado, Duarte, & Malta, 2010). To ensure intra-analyzer reliability, data were re-digitized by the same experimenter after one month. Spearman’s correlation procedures revealed high reliability levels for x and y coordinates (r = .98, and r = .97, respectively).
Three angular measures were analyzed to examine how the angular relationship between players during futsal performance constrained ball velocity in the trajectory of a pass (see Figure 1). These variables included the possible combinations of the passing vector (i.e., the imaginary line connecting ball carrier to the ball receiver) with three different interception vectors: 1) vector of the ball carrier to the nearest defender, 2) vector of the ball carrier to the ball receiver’s nearest defender, and 3), vector of the ball receiver to the nearest defender. Each vector was obtained through the equation 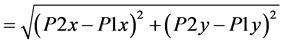 , where “a” refers to the distance between players (P1 and P2). From the distance values, the angles were calculated by
, where “a” refers to the distance between players (P1 and P2). From the distance values, the angles were calculated by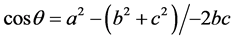 .
.
Thus, the interaction of the aforementioned passing vector with each of the interception vectors (1, 2, 3) resulted, respectively, in the angles A, B, and C (Figure 1):
A) Passing vector angle to the ball carrier-nearest defender’s vector;
B) Passing vector angle to the ball carrier-teammate’s nearest defender’s vector;
C) Passing vector angle to the teammate-nearest defender’s vector.
From the displacement coordinates of the players and the ball, the angles A, B, and C were computed at two consecutive moments: 1) initial, i.e. at the moment the ball carrier received the ball, and 2), final, i.e. at the moment he initiated the pass. Next, we analysed the spatiotemporal characteristics of each angle regarding the initial and final moments by their rate of spatial change over time. In this sense, angular velocity was obtained by vθ = (θF – θI)/Δt, where vθ was the angular velocity, θF was the final angle, θI was the initial angle, and Δt
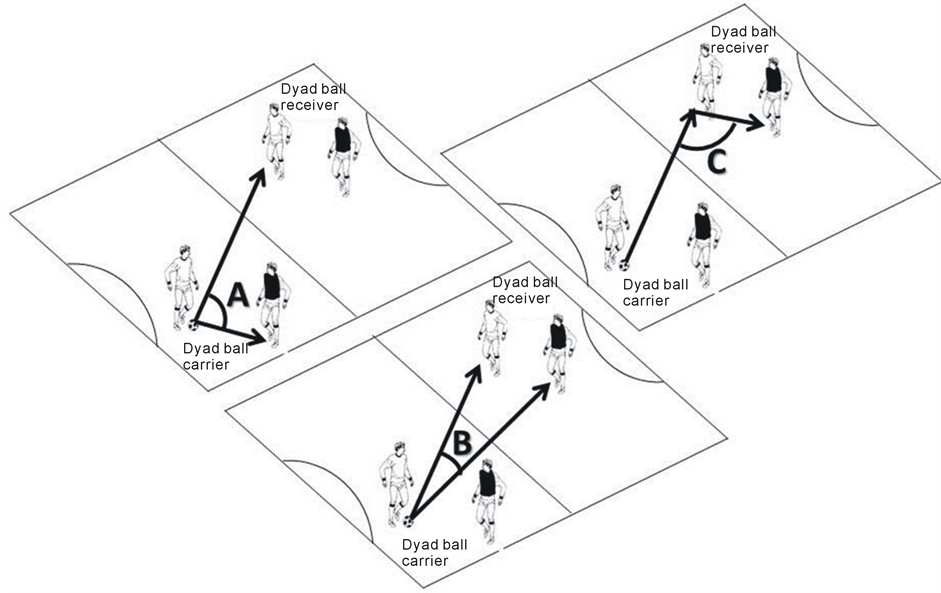
Figure 1. Illustration of the angles formed from the following interacting vectors: (A) Ball carrier to the ball receiver and ball carrier to the closest defender; (B) Ball carrier to the ball receiver and ball carrier to the ball receiver’ nearest defender; (C) Ball carrier to the ball receiver and ball receiver to the nearest defender.
referred to the time between initial and final angles. For our present purpose, negative velocity data signalled that the angle was closing, and positive velocity data referred to an opening angle. In this period, we also calculated angular variability through CV = s/x̅, where CV is the coefficient of variation, s refers to the standard deviation, and x̅ is the arithmetic mean.
Finally, passing velocity was computed by PV = │dPR–dPI│/Δt, where PV was passing velocity, dPR was the distance between attacking players at the moment the ball reception by the ball receiver, dPI was the distance between attacking players at the moment the passing initiation by the ball carrier, and Δt referred to the time between a ball carrier’s pass and a ball receiver’s reception of the ball.
2.3. Statistical Procedures
In order to understand the constraining influence of initial and final angles (A, B, and C), and their rates of change (velocities and variability) on regulation of passing velocity, each independent variable was split into four groups of equal size (G1, G2, G3, and G4), ordering data from lowest to highest values, and adopting quartiles as the cut-off points (Altman & Bland, 1994). Thus, the first group for each variable was composed of the seven observations with lowest scores of the relevant variable; the second group involved the next seven observations in ascending order, and so on (Table 1).
Since the statistical assumptions of normality and homogeneity of variance were not met in all sub-groups, confirmed with Shapiro-Wilks and Bartlett tests, respectively, inter-group comparisons were made through non-parametric procedures. The Kruskal-Wallis test, and the Mann-Whitney test were used to conduct pairwise comparisons (Siegel & Castellan Jr., 1988). All data analyses were undertaken with STATISTICA® 10.0 software (Stat Soft Inc., Tulsa, USA).
3. Results
Results presented in Figure 2 show the mean and confidence limit data for passing velocity with regard to the
Table 1. Ranges of values of the initial and final angles A, B and C, their velocities and variability pertaining to each group (G1, G2, G3, and G4).
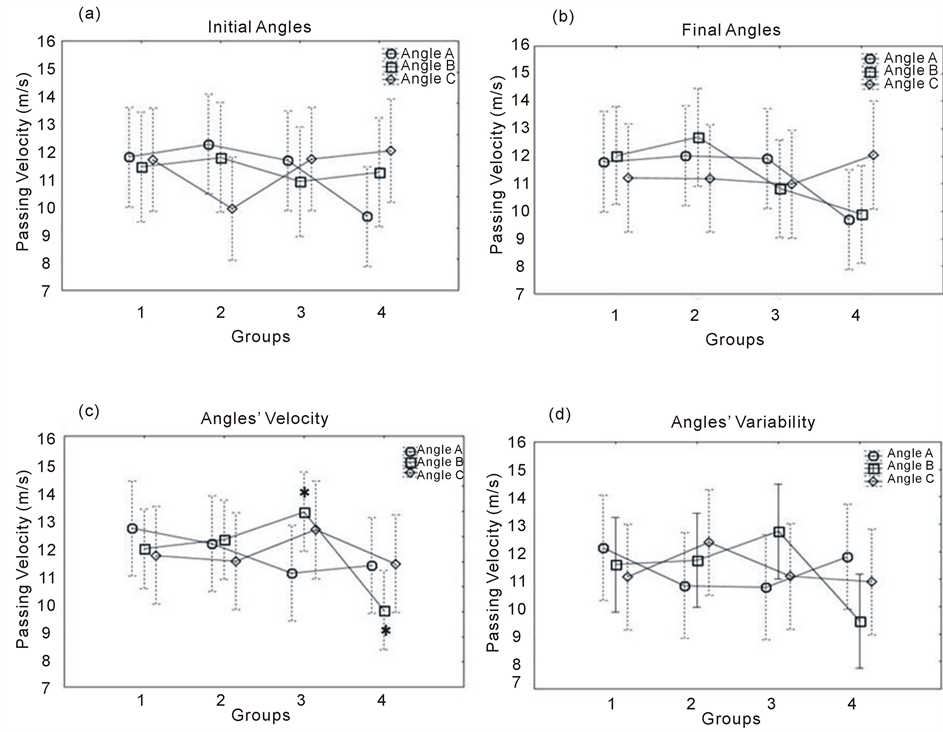
Figure 2. Means and confidence limit of passing velocity for the different values of (a) initial angles, (b) final angles (c) angles’ velocity, and (d) angles’ variability.
initial and final angles A, B, and C, and their rates of changes (velocity and variability). Regarding the descriptive statistical analyses, there was a clear tendency for passing velocity to be constrained by all those variables. Specifically, Figure 2(a) shows that the value of the initial angle A seemed to lead to a lower passing velocity in group 4 (fourth quartile) than in the other groups; furthermore, the value of the initial angle C appeared to result in a lower passing velocity in group 2 (second quartile) than in the other groups.
Concerning the angles at the moment the ball carrier initiated the pass (final angles), Figure 2(b) shows that angles A and B also seemed to lead to a lower value of passing velocity in group 4 (fourth quartile) than in the group C; moreover, the value of angle B appeared to result in a greater passing velocity in groups 1 and 2 (first and second quartiles) than in the other groups.
Finally, with regard to the rates of changes of angles A, B, and C, Figure 2(c) and Figure 2(d) show, respectively, that the angle B’ velocity and variability seemed to have constrained a lower passing velocity in group 4 (fourth quartile) than in the other groups.
The Kruskall-Wallis ANOVAs on each variable revealed significant difference in passing velocity only for the velocity of angle B (Table 2). The Mann-Whitney U test showed that passing velocity in the G1, G2 and G3 groups was higher than in G4: Z = 2.47, p = .04; Z = 2.04, p = .04; and Z = 2.81, p = .01, respectively (Figure 2).
4. Discussion
The aim of this study was to investigate the effects of angular positional constraints between attackers and defenders on decision-making of passing in the team sport of futsal. We considered how different relative angular values influenced the regulation of passing velocity in futsal. Results showed that the velocity of the change in the angle formed by the vectors ball carrier-ball receiver and ball carrier-ball receiver’s nearest defender seems to have acted as an informational variable that constrained the velocity of the ball during the pass. This result suggest that, for regulating passing velocity in a dynamic performance environment like futsal, an individual does not rely solely on information regarding the magnitude of angular gaps per se, i.e. angles at the moments the ball carrier received the ball and initiated the pass, but on their rate of spatial change over time. In other words, results suggested that participants’ decision-making on the velocity of passing was influenced by the
Table 2. Results of the Kruskal-Wall is test applied for groups in the initial and final angles A, B, and C, their velocities and variability.
velocity of change in the angular relationship between key performers over time. It seems that angular velocity might have provided the necessary information for the prospective control of movement in the ball carrier (Bastin, Craig, & Montagne, 2006; Corrêa et al., 2012b; Fajen, Riley, & Turvey, 2009).
These interpretations are in line with data outlining the influence of spatiotemporal measures, such as the time-to-contact and relative velocity information on decision-making in team games like basketball, football, futsal, and rugby union (see Correia & Araújo, 2009; Correia et al., 2011; Duarte et al, 2010a; Passos et al., 2008, 2009; Travassos et al., 2012; Watson et al., 2011). Similar to those above cited information, angular velocity could supply the essential information for players to make decisions because it couples space and time constraints, which afford prospective guidance of movements.
The changes of the angles A (ball carrier-ball receiver vector interacting with ball carrier-closest defender vector), and C (ball carrier-ball receiver vector interacting with ball receiver-closest defender vector) may not have resulted in information for the system, perhaps because these changes did not signal a risk of interception or a passing possibility for participants.
Concerning the velocity of change of angle B, it seems that the angular interaction pattern involving the ball carrier, ball receiver, and ball receiver’s marking defender was flexible enough to adapt to changes in angular values between performers, while maintaining passing velocity. Results showed that ball passing velocity remained at the same level when angular velocity was initially negative in value −18.16˚/s, changing to a positive value of 11.26˚/s. As previously described, the emergence of negative and positive angular velocities suggests, respectively, that the angle’s value was decreasing because the ball receiver and his marking defender were moving towards each other, or was increasing because the ball receiver and his marking defender were moving away from each other.
Based on this result it seems that passing velocity values remained the same since that angle remained within a critical threshold range. However, from that positive angle onwards the system seemed to enter in a new critical state allowing the emergence of a slower passing velocity (Corrêa et al., 2012a/b). Similar critical states have also been identified in attacker-defender dyadic systems manipulations in other team sports (see Passos et al., 2009b for details).
5. Conclusion
In summary, the findings of this study allowed us to conclude that passing velocity during competitive performance in futsal was regulated by the rate of change of an angle established by the interaction between the ball carrier to ball receiver vector with the ball carrier to ball receiver’s nearest defender vector. The data revealed that there was a critical threshold range of angular velocities values (−18.16˚/s to 11.26˚/s) in which the passing velocity did not change.
This study provides useful insights into the design of practice tasks in futsal, suggesting that: 1) the ability of players to make accurate decisions can be developed using information from the interactions between an individual and team mates and opponents in futsal; 2) passing drills involving the ball carrier, his teammate, and the teammate’s nearest defender could be vehicle for enhancing decision-making processes in team games, as well as ball passing skill; 3) ball carrier should be attuned to the velocities in angles between teammates and opponents in order to decide the passing velocity; 4) teammates could be advised to move away from their nearest defenders, but keeping the passing line. Further work is needed to verify this assumption.
Acknowledgements
This research was supported by the Capes Foundation, Ministry of Education of Brazil (BEX 3243/10-9), awarded to the first author. The authors wish to thank Prof. Ms. SérgioAparecido dos Santos for his mathematical support.
References
- Altman, D. G., & Bland, J. M. (1994). Statistics Notes: Quartiles, Quintiles, Centiles, and Other Quantiles. British Medical Journal, 309, 996. http://dx.doi.org/10.1136/bmj.309.6960.996
- Araújo D., Davids, K., Bennett, S., Button, C., & Chapman, G. (2004). Emergence of Sport Skills under Constraints. In: A. M. Williams, & N. J. Hodges (Eds.), Skill Acquisition in Sport: Research, Theory and Practice (pp. 409-433). London: Routledge, Taylor & Francis.
- Araújo, D., Davids, K., & Hristovski, R. (2006). The Ecological Dynamics of Decision Making in Sport. Psychology of Sport and Exercise, 7, 653-676. http://dx.doi.org/10.1016/j.psychsport.2006.07.002
- Bastin, J., Craig, C., & Montagne, G. (2006). Prospective Strategies Underlie the Control of Interceptive Actions. Human Movement Science, 25, 718-732. http://dx.doi.org/10.1016/j.humov.2006.04.001
- Corrêa, U. C., Alegre, F., Freudenheim, A. M., Santos, S., & Tani, G. (2012a). The Game of Futsal as an Adaptive Process. Nonlinear Dynamics, Psychology, and Life Sciences, 16, 185-204.
- Corrêa, U. C., Vilar, L., Davids, K., & Renshaw, I. (2012b). Informational Constraints on the Emergence of Passing Direction in the Team Sport of Futsal. European Journal of Sport Science, 14, 169-176. http://dx.doi.org/10.1080/17461391.2012.730063
- Correia, V., & Araújo, D. (2009). Tau Influence on Decision Making in Basketball. Revista de Psicologíadel Deporte, 18, 475-479.
- Correia, V., Araújo, D., Craig, C., & Passos, P. (2011). Prospective Information for Pass Decisional Behavior in Rugby Union. Human Movement Science, 30, 984-997. http://dx.doi.org/10.1016/j.humov.2010.07.008
- Davids, K., & Araújo, D. (2010). The Concept of “Organismic Asymmetry” in Sport Science. Journal of Sports Science and Medicine, 13, 663-640. http://dx.doi.org/10.1016/j.jsams.2010.05.002
- Davids, K. (2009). The Organization of Action in Complex Neurobiological Systems. In Araújo, D., Ripoll, H., & Raab, M. (Eds.), Perspectives on Cognition and Action in Sport (pp. 3-13). New York: Nova Science Publishers, Inc.
- Davids, K., Button, C., Araújo, D., Renshaw, I., & Hristovski, R. (2006). Movement Models from Sports Provide Representative Task Constraints for Studying Adaptive Behavior in Human Movement Systems. AdaptiveBehavior, 14, 73-95. http://dx.doi.org/10.1177/105971230601400103
- Duarte, R., Araújo, D., Gazimba, V., Fernandes, O., Folgado, H., Marmeleira, J., & Davids, K. (2010a). The Ecological Dynamics of 1v1 Sub-Phases in Association Football. The Open Sports Sciences Journal, 3, 16-18. http://dx.doi.org/10.2174/1875399X01003010016
- Duarte. R., Araújo, D., Fernandes, O., Fonseca, C., Correia, V., Gazimba, V., Travassos, B., Esteves, P., Vilar, L., & Lopes, J. (2010b). Capturing Complex Human Behaviors in Representative Sports Contexts with a Single Camera. Medicina (Kaunas), 46, 408-414.
- Esteves, P., Oliveira, R., & Araújo, D. (2011). Posture-Related Affordances Guide Attack in Basketball. Psychology of Sport and Exercise, 12, 639-644. http://dx.doi.org/10.1016/j.psychsport.2011.06.007
- Fajen, B. R., Riley, M. A., & Turvey, M. T. (2009). Information, Affordances, and the Control of Action in Sport. International Journal of Sport Psychology, 40, 79-107.
- Fajen, B., & Turvey, M. (2003). Perception, Categories, and Possibilities for Action. AdaptiveBehavior, 11, 276-278. http://dx.doi.org/10.1177/1059712303114004
- Fernandes, O., Folgado, H., Duarte, R., & Malta, P. (2010). Validation of the Tool for Applied and Contextual Time-Series Observation. International Journal of Sport Psychology, 41, 63-64.
- Gibson, J. J. (1986). The Ecological Approach to Visual Perception. London: Cornell University Press.
- Gréhaigne, J.-F., Godbout, P., & Bouthier, D. (2001). The Teaching and Learning of Decision Making in Team Sports. Quest, 55, 59-76. http://dx.doi.org/10.1080/00336297.2001.10491730
- Griffin, L. L., & Butler, J. (2005). Teaching Games for Understanding: Theory, Research, and Practice. Champaign, IL: Human Kinetics.
- Hughes, M., Dawkins, N., David, R., & Mills, J. (1998). The Perturbation Effect and Goal Opportunities in Soccer. Journal of Sports Sciences, 16, 20-21.
- McGarry, T. (2009). Applied and Theoretical Perspectives of Performance Analysis in Sport: Scientific Issues and Challenges. International Journal of Performance Analyses in Sport, 9, 128-140.
- McGarry, T., & Franks, I. M. (1996). In Search of Invariant Athletic Behaviour in Competitive Sport Systems: An Example from Championship Squash Match-Play. Journal of Sports Sciences, 14, 445-456. http://dx.doi.org/10.1080/02640419608727730
- McGarry, T., Anderson, D. I., Wallace, S. A., Hughes, M., & Franks, I. M. (2002). Sport Competition as a Dynamical SelfOrganizing System. Journalof Sports Sciences, 20, 771-781. http://dx.doi.org/10.1080/026404102320675620
- Passos, P., Araújo, D., Davids, K., Gouveia, L., Milho, J., & Serpa, S. (2008). Information-Governing Dynamics of AttackerDefender Interactions in Youth Rugby Union. Journal of Sports Sciences, 26, 1421-1429. http://dx.doi.org/10.1080/02640410802208986
- Passos, P., Araújo, D., Davids, K., Gouveia, L., Milho, J., & Serpa, S. (2009b). Interpersonal Coordination Tendencies, Decision-Making and Information Governing Dynamics in Rugby Union. In Araújo, D., Ripoll, H., & Raab, M. (Eds.). Perspectives on Cognition and Action in Sport (pp. 27-42). New York: Nova Science Publishers, Inc.
- Passos, P., Araújo, D., Davids, K., Gouveia, L., Serpa, S., Milho, J., & Fonseca, S. (2009). Interpersonal Pattern Dynamics and Adaptive Behavior in Multiagent Neurobiological Systems: Conceptual Model and Data. Journal of Motor Behavior, 41, 445-459. http://dx.doi.org/10.3200/35-08-061
- Richardson, M., Marsh, K., & Baron, R. (2007). Judging and Actualizing Intrapersonal and Interpersonal Affordances. Journal of Experimental Psychology: Human Perception and Performance, 33, 845-859. http://dx.doi.org/10.1037/0096-1523.33.4.845
- Siegel, S., & Castellan Jr., N. J. (1988) Nonparametrics Statistics (2nd ed.). New York: Mc Graw-Hill Int.
- Travassos, B., Araújo, D., Davids, K., Vilar, L., Esteves, P., & Vanda, C. (2012). Informational Constraints Shape Emergent Functional Behaviours during Performance of Interceptive Actions in Team Sports. Psychology of Sport and Exercise, 13, 216-223. http://dx.doi.org/10.1016/j.psychsport.2011.11.009
- Turner, A., & Martinek, T. J. (1995). Teaching for Understanding: A Model for Improving Decision Making during Game Play. Quest, 47, 44-63. http://dx.doi.org/10.1080/00336297.1995.10484144
- Vilar, L., Araújo, D., Davids, K., & Button, C. (2012). The Role of Ecological Dynamics in Analysing Performance in Team Sports. Sports Medicine, 42, 1-10. http://dx.doi.org/10.2165/11596520-000000000-00000
- Watson, G., Brault, S., Kulpa, R., Bideau, B., Butterfield, J., & Craig, C. (2011). Judging the “Passability” of Dynamic Gaps in a Virtual Rugby Environment. Human Movement Science, 30, 942-956. http://dx.doi.org/10.1016/j.humov.2010.08.004
- Winter, D. A. (2005). Biomechanics and Motor Control of Human Movement (3rd ed.). New York: John Wiley & Sons, Inc.


