World Journal of Engineering and Technology
Vol.02 No.04(2014), Article ID:51628,8 pages
10.4236/wjet.2014.24032
Optimization of an Ammonia Synthesis Converter
Jackson Gunorubon Akpa*, Nwokoma Raphael Raphael
Department of Chemical/Petrochemical Engineering, Rivers State University of Science and Technology, Port-Harcourt, Nigeria
Email: *jacksonakpa@yahoo.com, rakendy@yahoo.com
Academic Editor: Hristo Sapoundjiev, Natural Resources Canada, Canada
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 September 2014; revised 13 October 2014; accepted 3 November 2014
ABSTRACT
A scheme that optimizes the converter of an ammonia synthesis plant to determine optimal inlet temperatures of the catalyst beds has been developed. The optimizer maximizes an objective function—The fractional conversion of nitrogen on the four catalyst beds of the converter subject to variation of the inlet temperature to each catalyst bed. An iterative procedure was used to up- date the initial values of inlet temperature thus ensuring accurate results and quick convergence. Converter model results obtained with optimized operating conditions showed significant in- crease in fractional conversion of 42.38% (from 0.1949 to 0.2586), increased rate of reaction evi- dent in a 13.18% (0.5317 to 0.4616) and 23.84% (0.1946 to 0.1482) reduction in reactants (hy- drogen and nitrogen) concentration respectively and a 56.48% increase (from 0.1181 to 0.1838) in ammonia concentration at the end of the fourth catalyst bed compared to results obtained with industrial operating conditions.
Keywords:
ammonia synthesis converter, optimization, optimal inlet bed temperatures

1. Introduction
The need to operate process equipments at optimal conditions that ensures efficient performance and economic competitiveness of products of similar industries is a growing challenge to process designers and entrepreneurs of industries. An optimal set of design and operating parameters ensures that the industry/system functions in the most efficient way. One way of achieving this is through optimization. Optimization is a widely used engineer- ing tool for enhancing efficiency and performance of systems. It is the process of determining the operating conditions of a process/system’s parameters that ensures the most efficient operation of the system/process by adjusting the process parameters so as to maximize some specified set of parameters or one or more of the pro- cess specifications while keeping all others within their constraints. The improved efficiency/performance can be measured by the reduction in production cost, increase in profit or increase in the quantity of products pro- duced. Operating parameters usually optimized include process variables such as flow rates, pressures, tempera- tures or equipment size such as volume, length and catalyst volume.
Optimization involves minimizing or maximizing an objective function; in most optimization problems, the objective function could be an economic return or term based on some parameters of the system, minimizing a cost function or maximizing a profit function; Optimizing the efficiency of the system by minimizing or max- imizing parameters that indicates performance of the system viz: minimize specific energy consumption [1] , op- timize maximum energy output [2] , minimum catalyst volume obtained to satisfy the production capacity at specified operating conditions [3] , maximum mass flow rate of production using a generic algorithm at optimal conditions of inlet temperature, total feed flow rate and operating pressure [4] , optimize reactor performance by varying its quench flows: Temperature and flow rate [5] , obtain optimum reactor length [6] [7] that gives the max- imum profit with objective function being: a function of the process parameters (heating value of product and feed gas) and reactor capital cost [8] .
The ammonia synthesis converter is a major component of the ammonia synthesis loop. Steady state one di- mensional pseudo-homogeneous models of an axial flow four catalyst bed ammonia synthesis converter were successfully developed by Akpa and Raphael [9] . The industrial plant data of Notore Chemical Industries Li- mited, located in Onne, Rivers State, Nigeria was used to run the developed simulation program (converter si- mulator) [9] . The developed model predicted a fractional conversion of 19.49% against the industrial plant out- put of 18.19%. This low output has necessitated the need for the optimization of the converter aimed at im- provement in the converter performance by investigating new operational conditions/parameters that will result in improved higher conversion of the reactants to product.
In this work, a parameter that indicates directly the efficiency of the converter—the fractional conversion of the reactants to products is optimized. The model equation that predicts the fractional conversion of reactants to products is used as the objective function to be maximized.
2. Methodology
In an earlier work by Akpa and Rapheal [9] , models that accurately predicted the performance (concentration of reactants and products, fractional conversion and Temperature progression along the catalyst beds) of the con- verter were developed. In the simulation study performed on the converter, effects of process parameters (feed flow rate, inlet temperature and pressure) on the converter performance were investigated. The inlet tempera- tures of each catalyst bed were observed to be very sensitive to the performance of the converter. The outlet temperature of a previous bed obtained from model equation was quenched to correspond to the industrial value of the inlet temperature of the next bed.
However in this optimization; an optimum inlet temperature of each bed which will result in the highest frac- tional conversion, lowest reactant concentration and highest product concentration was determined.
A constrained non-linear optimization procedure was used to determine the optimum inlet temperatures of the four catalyst beds which maximize the objective function (model equation that predicts the fractional conversion of the ammonia converter).
The objective function to be maximized is:
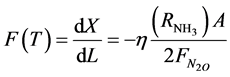 (1)
(1)
Subject to the values of the inlet Temperature:
 (2)
(2)
where A = cross-sectional area of the bed (m2); X = fractional conversion of Nitrogen; 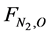 = initial flow rate (mole/hr) of nitrogen reactant; L = length of bed (reactor) (m);
= initial flow rate (mole/hr) of nitrogen reactant; L = length of bed (reactor) (m); 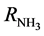 = rate of production of ammonia (NH3);
= rate of production of ammonia (NH3); 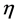 = effectiveness factor; Tind. = industrial plant inlet temperature; TDesign = design inlet temperature; Tinlet = inlet temperature of bed.
= effectiveness factor; Tind. = industrial plant inlet temperature; TDesign = design inlet temperature; Tinlet = inlet temperature of bed.
Where the reaction rate expression of Temkin-Pyzhez expressed in terms of activities by Dyson and Simon [10] had been expressed in terms of fractional conversion of the limiting reagent (nitrogen) by Akpa and Ra- phael [9] as:
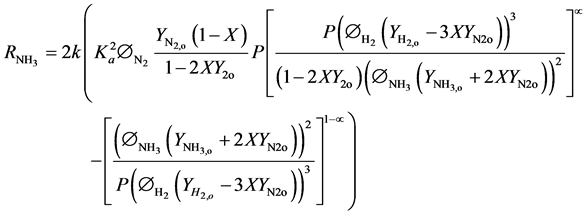 (3)
(3)
Other parameters in this equation can be obtained following the methods outlined in Akpa and Raphael [9] .
The industrial values of the inlet temperature of each bed were used as starting guesses, with maximum possi- ble value being the maximum value of the design temperature for the reactor and catalyst (823 K) above which the catalyst would begin to sinter [11] . Having established the lower and upper bounds of the constraint; a bracketing procedure [12] was employed to narrow the bracket until the inlet temperature value which satisfies (maximizes) the objective function was obtained. This ensures quick convergence and reasonable values of the inlet temperatures. The bisection method [13] was used to update the initial values of the inlet temperature of each bed using two initial guesses thus:
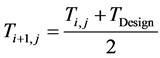 (4)
(4)
where:
 is the present value of the inlet Temperature of Bed j.
is the present value of the inlet Temperature of Bed j.
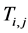 is the previous value of the inlet Temperature of Bed j.
is the previous value of the inlet Temperature of Bed j.
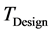 is the value of design inlet Temperature.
is the value of design inlet Temperature.
An algorithm developed to solve this optimization problem is shown below:
Process Optimization algorithm
Step 1: Guess initial inlet temperature of bed (industrial inlet temperature of each bed)
Step 2: Optimize converter bed j (j = 1, 2, 3, 4)
Determine converter performance:
Solve objective function to obtain fractional conversion of reactants in Bed j: equation (1)

using the program “CONVERTER SIMULATOR” [9] .
The converter simulation program [9] also solves the model equation for the temperature progression along any catalyst Bed j:
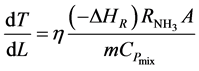 (4)
(4)
Equation (4) gives the outlet temperature of each bed.
Step 3: Update value of the inlet temperature using the bisection method
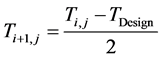
Step 4: Optimize converter Bed j using present inlet temperature value
Solve objective function to obtain fractional conversion of reactants in Bed j: equation (1)

using the program “CONVERTER SIMULATOR” [9] .
The converter simulation program [9] also solves the model equation for the temperature progression along any catalyst Bed j: equation (4)

Step 5: Check if objective function has been maximized:
Compare present 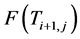 and previous
and previous 
Step 6: If answer to Step 5 is “YES”:
Optimum inlet of Bed j has been obtained.
If answer to Step 5 is “NO”:
Repeat Steps 3, 4, 5 and 6.
The steps above were followed to develop the optimization algorithm flow chart shown in Figure 1. A MathLab program was developed (Converter Optimizer) to solve the constrained nonlinear optimization problem following the algorithm flow chart.
Having obtained the optimum input/quench temperatures to Bed 1, 2, 3 and 4, these values (optimum temper- atures) were then used to run the converter simulator program [9] to obtain the conversion, temperature varia- tions and concentrations of the reactants (nitrogen N2, hydrogen H2) and product (ammonia NH3) at any point in the converter. The maximum conversion recorded at the end of Bed 4 is now taken as the optimum for the converter.
3. Discussion of Results
3.1. Effect of Inlet Temperature on Conversion in Each Bed
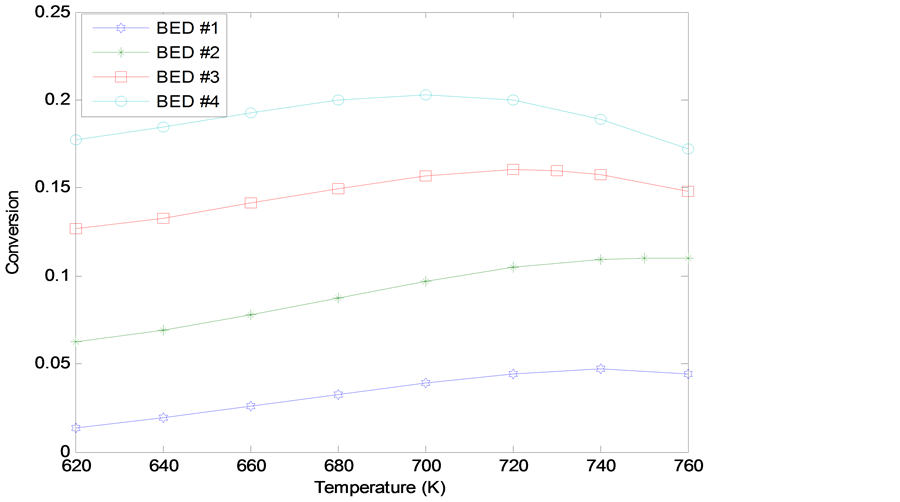
The result of optimization of the four catalyst beds of the converter by solving the objective function at varying inlet bed temperatures to obtain outlet fractional conversion for each catalyst bed is shown in Figure 2.
Figure 2 shows that the fractional conversion on each catalyst bed increases with increase in inlet temperature to a maximum point where further increase in inlet temperature results in a decrease in conversion. Thus it establishes the inlet temperature corresponding to this optimum conversion. The inlet temperature corresponding to the maximum conversion in a given bed is the optimum temperature of that bed. These optimum inlet temper- atures from Figure 2 are: Bed 1: 740 K with a maximum conversion of 5.70%; Bed 2: 750 K with a maximum conversion of 11.75%; Bed 3: 720 K with a maximum conversion of 17.66%; Bed 4: 700 K with a maximum conversion of 25.86%.
3.2. Effect of Optimum Inlet Temperatures on Percent Conversion
Having obtained the optimum inlet temperatures for each catalyst bed, the simulation program earlier developed by Akpa and Raphael [9] was used to obtain the optimum conversion, temperature progression and reactant and product concentrations along each catalyst bed. These converter performance parameters are shown in Figures 3-5 respectively.
Figure 3 shows a steady increase in conversion along each catalyst bed and Figure 4 shows the entire temperature of the four catalyst beds of the ammonia converter—tempearture at the inlet, within and at the outlet of the catalyst beds while Figure 5 shows the concentrations of the reactants (hydrogen and nitrogen) and pro- duct (ammonia) along each catalyst bed of the converter. The reactants decreased in concentration while the concentration of the product increased.
A comparison of the model prediction of converter performance using values of inlet bed temperatures from optimization results and industrial plant values [9] are presented in Table 1 (fractional conversion and inlet and outlet temperature temperature) and Table 2 (concentration of reactants (Nitrogen and Hydrogen) and product (Ammonia)).
Table 1 and Table 2 show the possible improvements in the converter performance when operated at the op- timum conditions as predicted from the optimization performed on the converter.
Figure 1. Flow algorithm for converter optimization.
Figure 2. Effect of inlet temperature on conversion at the end of each catalyst bed.
Figure 3. Fractional conversion along the catalyst beds.
Table 1. Comparison of optimization results with model prediction.
Figure 4. Temperature variation along the catalyst beds.
Figure 5. Concentration of reactants and product along the beds at optimum inlet tempera- tures.
Table 2. Comparison of optimization results with model prediction.
Table 1 shows that operating the converter at optimum conditions obtained from the optimization program results in an increase in the fractional conversion of the reactants to product from 0.1949 as predicted by model using industrial conditions to 0.2586 using optimized conditions. This corresponds to a 42.38% increase from predictions using industrial conditions. The inlet temperatures at the optimum conditions were higher for the first three beds and lower for the fourth bed when compared with the industrial inlet temperatures. Increase in optimum inlet temperatures were also reported in the works of Saddiq et al. [2] . The outlet temperature at the end of the fourth catalyst bed also decreased from 742.87 K to 716.60 K indicating more efficient heat utiliza- tion resulting in a reduction in temperature.
Table 2 also shows that operating converter at optimized conditions result in reduction in reactants concentra- tion in each bed (increased rate of reaction) culminating in a 13.18% (0.5317 to 0.4616 for the Hydrogen) and 23.84% (0.1946 to for the Nitrogen) concentration respectively at the end of the fourth catalyst bed; while the concentration of ammonia (the product) increased by 56.48% (from 0.1181 to 0.1838).
These results (increase in fractional conversion, reduction in reactants concentration and increase in product concentration) show improvements in converter efficiency when operated at optimized conditions.
4. Conclusions
One dimensional model was used for the optimization of the optimizations of an ammonia converter was per- formed to determine optimal inlet temperatures of the catalyst bed that will maximize an objective func- tion—model equation that predicts the fractional conversion of the catalyst beds of the converter. The optimum inlet temperatures of the catalyst beds obtained were used as operating conditions for the converter. The conver- ter model equations using these new optimum inlet temperatures predicted improved efficiency (42.38% in- crease in fractional conversion and 56.48% increase in ammonia concentration) compared with results obtained using industrial inlet catalyst bed temperature values.
An unsteady state and or two dimensional model of the ammonia converter are proposed for future study and simulation of the converter. The optimization procedure developed in this work can also be used for optimiza- tion of processes/systems.
References
- Modi, P.I. and Bhagchandani, C.G. (2013) Ammonia Plant Analysis. International Journal of Scientific Engineering and Technology, 2, 303-306.
- Saddiq, S., Khushnood, S., Koreshi, Z.Y., Shah, M.T. and Qureshi, A.H. (2013) Optimal Energy Recovery from Am- monia Synthesis in a Solar Thermal Power Plant. Arabian Journal for Science and Engineering, 38, 2569-2577.
- Ye, Q., Ying, W. and Fang, D. (2001) Simulation and Design Optimization of Ammonia Synthesis Converter. Chinese Journal of Chemical Engineering, 9, 441-446.
- Azarthoosh, M.J., Farivar, F. and Ale Ebrahim, H. (2014) Simulation and Optimization of a Horizontal Ammonia Synthesis Reactor Using Genetic Algorithm. RSC Advances, 4, 13419-13429. http://dx.doi.org/10.1039/c3ra45410j
- Sadeghi, M.T. and Kavianboroujeni, A. (2009) The Optimization of an Ammonia Synthesis Reactor Using Genetic Algorithm. International Journal of Chemical Reactor Engineering, 6.
- Borges, A.R., Lobato, S.F. and Steffen, V. (2012) Modeling and Optimization of an Auto-Thermal Ammonia Synthesis Reactor Using the Gravitational Search Algorithm. Proceedings EngOpt 3rd International Conference on Engineering Optimization, Rio de Janeiro.
- Babu, B.V. and Angira, R. (2005) Optimal Design of an Auto-Thermal Ammonia Synthesis Reactor. Computers and Che- mical Engineering Journal, 29, 1041-1045. http://dx.doi.org/10.1016/j.compchemeng.2004.11.010
- Ksasy, M.S.M., Areed, F., Saraye, S. and Khalik, M.A. (2010) Optimal Reactor Length of an Auto-Thermal Ammonia Synthesis Reactor. International Journal of Electrical & Computer Science, 10, 6-11.
- Akpa, J.G. and Raphael, N.R. (2014) Simulation of an Ammonia Synthesis Converter. Canadian Journal of Pure & Applied Sciences, 8, 2913-2923.
- Dyson, D.C. and Simon, J.M. (1986) A Kinetic Expression with Diffusion Correction for Ammonia Synthesis on In- dustrial Catalyst. Ind. Eng. Chem. Fundamental, 7, 605-610. http://dx.doi.org/10.1021/i160028a013
- Elnashaie, S.S.E.H. and Ajhabden, F.M. (1989) A Computer Software Package for the Simulation and Optimization of an Industrial Ammonia Converter Based on a Rigorous Heterogeneous Model. Mathematical and Computer Modeling, 12, 1589-1600. http://dx.doi.org/10.1016/0895-7177(89)90335-X
- Edgar, T.F., Himmelblau, D.M. and Lasdon, L.S. (2001) Optimization of Chemical Processes. 2nd Edition, McGraw- Hill, New York.
- Kuye, A. (1994) Optimisation Techniques for Engineers and Management Scientists. NAWA Publishers, Port-Harcourt.
Nomenclature
A: Cross sectional area (m2)

K: Rate constant for the reverse reaction
Ka: Equilibrium constant
L: Length of converter bed (m)
M: Total mass flow rate (KJ/kmol)
P: Operating pressure (Bar)
Ri: Rate of reaction with respect to component i
T: Temperature (K)
X: Fractional conversion of nitrogen
Yi: Mole fraction of component i


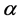
NOTES
*Corresponding author.