Advances in Materials Physics and Chemistry
Vol.3 No.2(2013), Article ID:32656,7 pages DOI:10.4236/ampc.2013.32020
Recalculate Structural, Elastic, Electronic, and Thermal Properties in LaAlO3 Rhombohedral Perovskite
Laboratory of Physico-chemical Studies, University of Saida, Saida, Algeria
Email: boudaliabdel@yahoo.fr, *Abdelkader1954@live.fr
Copyright © 2013 Abdelkader Boudali et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 19, 2013; revised May 5, 2013; accepted May 20, 2013
Keywords: Ab-Initio Calculations; Elastic Properties; Electronic Structure; Thermodynamic
ABSTRACT
We study the structural, elastic and electronic properties of perovskite insulator LaAlO3 using two different methods: the full-potential linearized augmented plane wave method and the pseudo-potential plane wave scheme in the frame of generalized gradient approximation and local density approximation GGA + mBJ. We have evaluated the ground state quantities. Also, we have presented the results of the band structure and densities of states. These results are in favourable agreement with previous theoretical works and the existing experimental data. To complete the fundamental characteristics of this compound, we have analyzed the thermodynamic properties.
1. Introduction
Lanthanum aluminate (LaAlO3) is a promising alternative gate dielectric for the replacement of SiO2 in silicon MOSFETs due to its high-k value (~25) [1], wide energy band gap (~5 - 6 eV) [2,3], large optical band gap 6.2 eV [2-4] and good thermal stability in contact with Si [5,6]. Being a perovskite (ABO3), LaAlO3 is also structurally compatible with many functional compounds, like manganites, superconductors and ferroelectrics. There have been many studies of the electronic and structural properties of LaAlO3, both of experimental [7-16] and theoretical aspects of bulk [17-22] as well as surface [23-26]. The structure of LaAlO3 is rhombohedral at room temperature and usually defined as hexagonal with space group R-3c (No.167). The lattice parameters are a = 0.536 nm and c = 1.311 nm [27] Figure 1.
To the best of our knowledge, there are no theoretical reports on the thermal behaviour of LaAlO3 in the literature. Consequently, the primary purpose of this work is to provide some additional information to the existing data on the physical properties of LaAlO3 with state-of the-art first-principles calculations. After introducing the problem, the remaining paper is organized as follows: in Section 2, we describe the calculation procedure. Results are presented in Section 3. Section 4 contains the conclusion.
2. Theoretical Method
The zero-temperature energy calculations are performed using both the all-electron full-potential linear augmented-plane-wave method (FP-LAPW) [28] and the plane-wave pseudopotential (PPs-PW) [29] method. In both cases exchange-correlation effects were described using the Perdew et al. (GGA96) form [30] and local density approximation Tr-Blaha LDA + mBJ [31]. The FP-LAPW calculations have been carried out using the WIEN2k code [28]. The sphere radii used in the calculations are 2.32, 1.74 and 1.60 a.u. for La, Al and O, respectively. Within these spheres, the charge density and potential are expanded in terms of crystal harmonics up to angular momenta L = 10, and a plane wave expansion has been used in the interstitial region. The Brillouin zone integrations for the total energy have been carried out using 35 special k-points in the irreducible Brillouin zone. Well converged solutions were found for RcutKmax = 8, where Kmax is the plane wave cut-off and Rcut is the atomic sphere radii. Both the muffin-tin radius and the number of k-points are varied to ensure convergence. Core states are treated fully relativistic but for valence states relativistic effects have been included in a scalar relativistic treatment.
The PP-PW calculations were performed using the CASTEP computer code [29,32] and the thermodynamic properties of LaAlO3, we apply the quasi-harmonic Debye model [33-41], in which the non-equilibrium Gibbs
 (a)
(a) (b)
(b)
Figure 1. Structure of rhombohedral hexagonal (a cell conventional and b cell primitive).
function G*(V; P, T) details can be found in my article Cubic LaAlO3 [33].
3. Results and Discussions
3.1. Structure and Elastic Constants
We firstly calculate the structural and elastic properties using FP-LAPW and PPs-PW methods. Figure 2 shows the variation of the total energy as a function of volume and fitted to a Murnaghan equation of state [42] to obtain the equilibrium lattice constant, bulk modulus, and its pressure derivative. The results are summarized in Table 1, together with some theoretical results and the available experimental data. Obviously, the obtained results by FP-LAPW method are in better agreement with the
 (a)
(a) (b)
(b)
Figure 2. Variations of the energy with the unit cell volume and c/a.

Table 1. Lattice constant a, bulk modulus B, pressure derivative of bulk modulus B’ and elastic constants parameters.
experiment compared to those calculated by PP-PW. The elastic constants are summarized in Table 1, which are in good agreement with the theoretical results and the available experimental data. It is clearly seen that the results we have calculated by FP-LAPW are in better agreement with experiment compared to those calculated by PP-PW. Our data will be beneficial to future investigation. We have performed elastic constants, calculations with the PW-PP method using the CASTEP code. The obtained values are presented in Table 1. Unfortunately, to our knowledge, no other results are available in literature for comparison. In Table 2, we report CASTEP calculations of the atomic positions after relaxation.
3.2. Electronic Properties
Density of states and electronic band structure often provide sufficient information for a thorough characterization of the electronic properties of a material. The energy band structure, total and partial density of states of LaAlO3 were calculated by FP-LAPW method scheme in the frame of local density approximation Tr-Blaha + mBJ. From Figures 3 and 4, it appears that the main effect of TB-mBJ potential, with respect to GGA [43], is to shift up the unoccupied La d states. This is due to the kinetic-energy density term which increases the energy of unoccupied states and changes the corresponding band structure and density of states [44]. In PBE calculation [43], the states at the bottom of the conduction band derive from La d states hybridized with the states of the La f band which occur just above the conduction band edge. In our TB-mBJ calculations, the La d unoccupied states are shifted to higher energies. This give rise to pure and narrower band of La f localized states at the bottom of the conduction band. Similar observations had been made by D. J. Singh for La2O3 [45]. Our calculations show that the valence band maximum is located at G and the conduction band is minimum at G point.

Figure 3. Band structure for high-symmetry directions in the Brillouin zone. The zero of energy corresponds to the fermi level.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 4. Calculated partial density of states and total density of states of LaAlO3.

Table 2. Positions of the atoms obtained by relaxation.
From Figure 4, we can find that the DOS can be mainly divided into four parts. The first part extending from −13.89 to −12.34 eV is of the combination of Al s, Al p, O s and La p states, and it is mainly due to the contribution of O s states; the second part from −6.73 to - 0 eV is mainly made from La p states, with slight contributions of O s; the third part from −7.3 to 0 eV is mainly the contribution of O 2p states; the forth part extending from 5.40 to 10 eV is mainly composed of La d and Al s, p states.
Our calculation show that the valence band maximum is located at G and the conduction band minimum is at G resulting in an direct gap of 5.4 eV in FP-LAPW, and 3.4 eV in PPs-PW, compared to 5.6 eV experimentally [2,3]. We have to remember that GGA is known to underestimate band gaps in semiconductors. Robertson et al. [22]. Who used a screen exchange (SX) GGA [23] found that LaAlO3 was a semiconductor with an indirect gap of 4.4 eV. Our calculation with LDA + mBJ shows that LaAlO3 is an insulator. This modification of the electronic properties implies automatically changes in the optical properties.
3.3. Thermodynamic Properties
The thermal properties are determined in the temperature range from 0 to 600 K, where the quasi-harmonic model remains fully valid. The pressure effect is studied in the 0 - 30 GPa range. The temperature effects on the lattice parameters are shown in Figure 5. The Volume parameter increases with increasing temperature but the rate of increase is very moderate. On the other hand, it is noted from Figure 6 that the relationships between bulk modulus and pressure are all nearly linear at various temperatures of 0, 100, 200, 300, 400, 500 and 600 K, respectively. The bulk modulus increases with pressure at a given temperature and decreases with temperature at given pressure. These results are due to the fact that the effect of increasing pressure on the material is the same as decreasing temperature of the material.
The investigation on the heat capacity of crystals is an old topic of condensed matter physics with which illustrious names are associated [46-48]. Knowledge of the heat capacity of a substance not only provides essential insight into its vibrational properties but is also mandatory for many applications. Two famous limiting cases are correctly predicted by the standard elastic continuum theory [48]. At high temperatures, the constant volume heat capacity Cv tends to the Petit and Dulong limit [49]. At sufficiently low temperatures, Cv is proportional to T3 [48]. At intermediate temperatures, however, the temperature dependence of Cv is governed by the details of vibrations of the atoms and for a long time could only be determined from experiments. Figures 7 and 8 represent the variation of the heat capacity, Cv (T), and volume expansion coefficient, a(T) as function of the temperature, respectively. These two quantities indicate a sharp increase up to ~400 K which is due to the anharmonic approximation of the Debye model used here. However, at higher temperature, the anharmonic effect on Cv is suppressed, and Cv is very close to the Dulong-Pettit
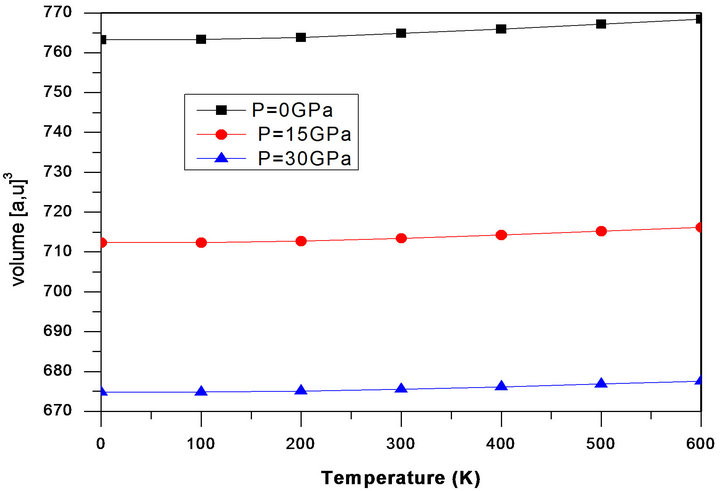
Figure 5. The relationships between lattice volumes and temperature at pressures of 0, 15 and 30 GPa, respectively.

Figure 6. The relationships between bulk modulus and temperature at pressures of 0, 15 and 30 GPa, respectively.

Figure 7. The heat capacity versus temperature at pressures of 0 GPa, respectively.

Figure 8. The thermal expansion versus temperature at pressures of 0, 15 and 30 GPa, respectively.
limit [49] (Cv(T)-3R for mono-atomic solids), which is common to all solids at high temperatures.
Finally, in Figure 8, we have plotted our results for the thermal expansion coefficient a of LaAlO3. It is shown that, for a given pressure, a increases with temperature at low temperatures especially at zero pressure and gradually tends to a linear increase at higher temperatures. As pressure increases, the increase of a with temperature becomes smaller. While for a given temperature, a decreases strongly with increasing pressure, and it is very small at higher temperatures and higher pressures.
4. Conclusion
In summary, the structural, elastic and electronic properties of perovskite isulator LaAlO3 at temperature T = 0 K were extensively studied using full-potential linearized augmented plane wave (FP-LAPW) as well as pseudopotential plane-wave (PPs-PW) method. The exchangecorrelation potential was calculated with the frame of generalized gradient approximation (GGA) and local density approximation Tr-Blaha + mBJ. The ground-state parameters, such as lattice parameter, bulk modulus and its pressure derivative and the elastic constants are in good agreement with some theoretical results and the available experimental data. The partial contribution of each atom to the total density of states was calculated. From the band structure, we find that LaAlO3 is a direct G→G gap close about 98% to the experimental value indicating that the material is an insulator. With this change of electronic properties, the optical properties must be recalculated. To complete the basic characteristics of this compound, we analyzed their thermodynamic properties using the quasiharmonic model of Debye. We see that the predicted heat capacity Cv is close to the Dulong-Petit limit, which is common to all solids at high temperatures.
REFERENCES
- B.-E. Park and H. Ishiwara, “Formation of LaAlO3 Films on Si (100) Substrates Using Molecular Beam Deposition,” Applied Physics Letters, Vol. 82, No. 8, 2003 pp. 1197-1199. doi:10.1063/1.1556966
- S. G. Lim, S. Kriventsov, T. N. Jackson, J. H. Haeni, D. G. Schlom, A. M. Balbashov, R. Uecker, P. Reiche, J. L. Freeouf and G. Lucovsky, “Dielectric Functions and Optical Bandgaps of High-K Dielectrics for Metal-OxideSemiconductor Field-Effect Transistors by far Ultraviolet Spectroscopic Ellipsometry,” Journal of Applied Physics, Vol. 91, No. 7, 2002, pp. 4500-4505. doi:10.1063/1.1456246
- X. Lu, Z. G. Liu, Y. P. Wang, Y. Yang, X. P. Wang, H. W. Zhou and B. Y. Nguyen, “Lattice Symmetry Applied in Transfer-Matrix Methods for Photonic Crystals,” Journal of Applied Physics, Vol. 94, No. 2, 2003, pp. 811-821. doi:10.1063/1.1587011
- P. Delugas, V. Fiorentini and A. Filippetti, “Dielectric Properties and Long-Wavelength Optical Modes of the High-κ Oxide LaAlO3,” Physical Review B, Vol. 71, No. 13, 2005, pp. 134302-134307. doi:10.1103/PhysRevB.71.134302
- L. F. Edge, D. G. S4chlom, S. A. Chambers, E. Cicerrella, J. L. Freeouf, B. Holländer and J. Schubert, “Measurement of the Band Offsets between Amorphous LaAlO3 and Silicon,” Applied Physics Letters, Vol. 84, No. 2, 2004, pp. 726-728 .doi:10.1063/1.1644055
- P. Sivasubramani, M. J. Kim, B. E. Gnade, R. M. Wallace, L. F. Edge, D. G. Schlom, H. S. Craft and J.-P. Maria, “Outdiffusion of La and Al from Amorphous LaAlO3 in Direct Contact with Si (001),” Applied Physics Letters, Vol. 86, No. 20, 2005, Article ID: 201901. doi:10.1063/1.1928316
- X. H. Zeng, L. H. Zhang, G. J. Zhao, J. Xu, Y. Hang, H. Y. Pang, M. Y. Jie, C. F. Yan and X. M. He, “Crystal Growth and Optical properties of LaAlO3 and Ce-Doped LaAlO3 Single Crystals,” Journal of Crystal Growth, Vol. 271, No. 1-2, 2004, pp. 319-324. doi:10.1016/j.jcrysgro.2004.07.032
- M. Losurdo, M. M. Giangregorio, M. Luchena, P. Capezzuto, G. Bruno, R. G. Toro, G. Malandrino, I. L. Fragalà and R. Lo Nigro, “Structural-Optical Study of High-Dielectric-Constant Oxide Films,” Applied Surface Science, Vol. 253, No. 1, 2006, pp. 322-327. doi:10.1016/j.apsusc.2006.06.004
- A. A. Demkov, R. Lui, X. Zhang and H. Loechelt, “Study of Aniline on a Si(111)7×7 Surface by Scanning Tunneling Microscopy,” Journal of Vacuum Science & Technology B, Vol. 18, No. 5, 2000, pp. 2335-2338. doi:10.1116/1.1310659
- H. Wadati, Y. Hotta, A. Fujimori, T. Susaki, H. Y. Hwang, Y. Takata, K. Horiba, M. Matsunami, S. Shin, M. Yabashi, K. Tamasaku, Y. Nishino and T. Ishikawa, “Hard X-Ray Photoemission Study of LaAlO3/LaVO3 Multilayers,” Physical Review B, Vol. 77, No. 4, 2008, Article ID: 045122. doi:10.1103/PhysRevB.77.045122
- R. A. B. Devine, “Infrared and Electrical Properties of Amorphous Sputtered (LaxAl1-x)2O3 Films,” Journal of Applied Physics, Vol. 93, No. 12, 2003, pp. 9938-9942. doi:10.1063/1.1576299
- V. V. Afanas’ev, A. Stesmans, C. Zhao, M. Caymax, T. Heeg and J. Schubert, Y. Jia, D. G. Schlom and G. Lucovsky, “Band Alignment between (100) Si and Complex Rare Earth/Transition Metal Oxides,” Applied Physics Letters, Vol. 85, No. 24, 2004, pp. 5917-5919. doi:10.1063/1.1829781
- B.-E. Park and H. Ishiwara, “Electrical Properties of LaAlO3/Si and Sr0.8Bi2.2Ta2O9/LaAlO3/Si Structures,” Applied Physics Letters, Vol. 79, No. 6, 2001, pp. 806-808. doi:10.1063/1.1380246
- Y. Y. Mi, Z. Yu, S. J. Wang, P. C. Lim, Y. L. Foo, A. C. H. Huan and C. K. Ong, “Epitaxial LaAlO3 Thin Film on Silicon: Structure and Electronic Properties,” Applied Physics Letters, Vol. 90, No. 18, 2007, Article ID: 181925. doi:10.1063/1.2736277
- V. Garcia, M. Bibes, J.-L. Maurice, E. Jacquet, K. Bouzehouane, J.-P. Contour and A. Barthélémy, “Spin-Dependent Tunneling through High-k LaAlO3,” Applied Physics Letters, Vol. 87, No. 21, 2005, Article ID: 212501. doi:10.1063/1.2132526
- E. Cicerrella, J. L. Freeouf, L. F. Edge, D. G. Schlom, T. Heeg, J. Schubert and S. A. Chambers, “Optical Properties of La-Based High-K Dielectric Films,” Journal of Vacuum Science & Technology A, Vol. 23, No. 6, 2005, pp. 1676-1680. doi:10.1116/1.2056555
- A. A. Knizhnik, I. M. Iskandarova, A. A. Bagatur’yants, B. V. Potapkin, L. R. C. Fonseca and A. Korkin, “FirstPrinciples Calculations of the Electrical Properties of LaAlO3 and Its Interface with Si,” Physical Review B, Vol. 72, No. 23, 2005, Article ID: 235329. doi:10.1103/PhysRevB.72.235329
- P. Delugas, V. Fiorentini and A. Filippetti, “Dielectric Properties and Long-Wavelength Optical Modes of the High-κ Oxide LaAlO3,” Physical Review B, Vol. 71, No. 13, 2005, Article ID: 134302. doi:10.1103/PhysRevB.71.134302
- P. W. Peacock and J. Robertson, “Band Offsets and Schottky Barrier Heights of High Dielectric Constant Oxides,” Journal of Applied Physics, Vol. 92, No. 8, 2002, pp. 4712-4721. doi:10.1063/1.1506388
- K. Xiong, J. Robertson and S. J. Clark, “Defect States in the High-Dielectric-Constant Gate Oxide LaAlO3,” Applied Physics Letters, Vol. 89, No. 2, 2006, Article ID: 022907. doi:10.1063/1.2221521
- K. Xiong, J. Robertson and S. J. Clark, “Electronic Defects in LaAlO3,” Microelectronic Engineering, Vol. 85, No. 1, 2008, pp. 65-69. doi:10.1016/j.mee.2007.01.181
- C. J. Först, K. Schwarz and P. E. Blöchl, “Structural and Electronic Properties of the Interface between the High-k Oxide LaAlO3 and Si (001),” Physical Review Letters, Vol. 95, No. 13, 2005, Article ID: 137602. doi:10.1103/PhysRevLett.95.137602
- J. L.Tang, J. Zhu, W. F. Qin, J. Xiong, Y. Zhang and Y. R. Li, “Atomic Relaxation and Electronic Redistribution of LaAlO3 (001) Surfaces,” Physics Letters A, Vol. 365, No. 1-2, 2007, pp. 149-155. doi:10.1016/j.physleta.2006.12.072
- R. Pentcheva and W. E. Pickett, “Charge Localization or Itineracy at LaAlO3/SrTiO3 Interfaces: Hole Polarons, Oxygen Vacancies, and Mobile Electrons,” Physical Review B, Vol. 74, No. 3, 2006, Article ID: 035112. doi:10.1103/PhysRevB.74.035112
- C. H. Lanier, J. M. Rondinelli, B. Deng, R. Kilaas, K. R. Poeppelmeier and L. D. Marks, “Surface Reconstruction with a Fractional Hole: (√5×√5)R26.6˚ LaAlO3 (001),” Physical Review Letters, Vol. 98, No. 8, 2007, Article ID: 086102. doi:10.1103/PhysRevLett.98.086102
- S. Gemming and G. Seifert, “SrTiO3 (001) LaAlO3 (001) Multilayers: A Density-Functional Investigation,” Acta Materialia, Vol. 54, No. 16, 2006, pp. 4299-4306 doi:10.1016/j.actamat.2006.05.023
- C. J. Howard, B. J. Kennedy and B. C. Chakoumakos, “Neutron Powder Diffraction Study of Rhombohedral Rare-Earth Aluminates and the Rhombohedral to Cubic Phase Transition,” Journal of Physics: Condensed Matter, Vol. 12, No. 4, 2000, pp. 349-365. doi:10.1088/0953-8984/12/4/301
- P. Blaha, K. Schwarz and P. Sorantin “Full-Potential, Linearized Augmented Plane Wave Programs for Crystalline Systems,” Computer Physics Communications, Vol. 59, No. 2, 1990, pp 399-415. doi:10.1016/0010-4655(90)90187-6
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, “First-Principles Simulation: Ideas, Illustrations and the CASTEP Code,” Journal of Physics: Condensed Matter, Vol. 14, No. 11, 2002. pp. 2717-2744. doi:10.1088/0953-8984/14/11/301
- J. P. Perdew, S. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996, pp. 3865-3868. doi:10.1103/PhysRevLett.77.3865
- F. Tran and P. Blaha, “Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential,” Physical Review Letters, Vol. 102, No. 22, 2009, Article ID: 226401. doi:10.1103/PhysRevLett.102.226401
- L. Kleinman and D. M. Bylander, “Efficacious Form for Model Pseudopotentials,” Physical Review Letters, Vol. 48, No. 20, 1982, pp. 1425-1428. doi:10.1103/PhysRevLett.48.1425
- A. Boudali, B. Amrani , M. Driss khodja, A. Abada and K. Amara, “First-Principles Study of Structural, Elastic, Electronic, and Thermal Properties of LaAlO3 Perovskite,” Computational Materials Science, Vol. 45, No. 4, 2009, pp. 1068-1072. doi:10.1016/j.commatsci.2009.01.011
- M. A. Blanco, E. Francisco and V. Luaña, “GIBBS: Isothermal-Isobaric Thermodynamics of Solids from Energy Curves Using a Quasi-Harmonic Debye Model,” Computer Physics Communications, Vol. 158, No. 1, 2004, pp. 57-72. doi:10.1016/j.comphy.2003.12.001
- M. A. Blanco, A. Martín Pendás, E. Francisco, J. M. Recio and R. Franco, “Thermodynamical Properties of Solids from Microscopic Theory: Applications to MgF2 and Al2O3,” Journal of Molecular Structure: THEOCHEM, Vol. 368, 1996, pp. 245-255. doi:10.1016/S0166-1280(96)90571-0
- M. Flórez, J. M. Recio, E. Francisco, M. A. Blanco and A. M. Pendás, “First-Principles Study of the Rocksalt-Cesium Chloride Relative Phase Stability in Alkali Halides,” Physical Review, Vol. 66, No. 14, 2002, pp. 144112- 144719.
- E. Francisco, J. M. Recio, M. A. Blanco and A. M. Pendás, “Quantum-Mechanical Study of Thermodynamic and Bonding Properties of MgF2,” The Journal of Physical Chemistry, Vol. 102, No. 9, 1998, pp. 1595-1601. doi:10.1021/jp972516j
- E. Francisco, M. A. Blanco and G. Sanjurjo, “Atomistic simulation of SrF2 polymorphs,” Physical Review, Vol. 63, No. 9, 2001, Article ID: 094107.
- J. P. Poirier, “Introduction to the Physics of the Earth’s Interior,” Cambridge University Press, Oxford, 2000. doi:10.1017/CBO9781139164467
- R. Hill, “The Elastic Behaviour of a Crystalline Aggregate,” Proceedings of the Physical Society, Vol. 65, No. 5, 1952, pp. 349-354. doi:10.1088/0370-1298/65/5/307
- N. Iles, A. Kellou, K. D. Khodja, B. Amrani, F. Lemoigno, D. Bourbie and H. Aourag, “Atomistic Study of Structural, Elastic, Electronic and Thermal Properties of Perovskites Ba(Ti,Zr,Nb)O3,” Computational Materials Science, Vol. 39, No. 4, 2007, pp. 896-902. doi:10.1016/j.commatsci.2006.10.012
- V. G. Tyuterev and N. Vast, “Murnaghan’s Equation of State for the Electronic Ground State Energy,” Computational Materials Science, Vol. 38, No. 2, 2006, pp. 350- 353. doi:10.1016/j.commatsci.2005.08.012
- X. Luo and B. Wang, “First-Principles Study of the Electronic and Optical Properties in Rhombohedral LaAlO3,” Journal of Applied Physics, Vol. 104, No. 5, 2008, Article ID: 053503. doi:10.1063/1.2973671
- D. Koller, F. Tran and P. Blaha, “Merits and Limits of the Modified Becke-Johnson Exchange Potential,” Physical Review, Vol. 83, No. 19, 2011, pp. 195134-195143. doi:10.1103/PhysRevB.83.195134
- D. J. Singh, “Electronic Structure Calculations with the Tran-Blaha Modified Becke-Johnson Density Functional,” Physical Review, Vol. 82, No. 20, 2010, pp. 205102-205119. doi:10.1103/PhysRevB.82.205102
- A. Einstein, “Die Plackschen Theorie der Strahlung und die Theorie der spezifischen Warme,” Annalen der Physik, Vol. 22, No. 2, 1907, pp. 180-190.
- W. Nernst, A. F. Lindemann and Z. Elektrochem, “Angew,” The Journal of Physical Chemistry, Vol. 17, No. 817, 1977.
- P. Debye, “The Theory of Specific Warmth,” Annalen Der Physik, Vol. 39, No. 14, 1912, pp. 789-839.
- A. T. Petit and P. L. Dulong, “Recherches sur Quelques Points Importants de la Théorie de la Chaleur,” Annales de Chimie et de Physique, Vol. 10, 1819, pp. 395-413.
- M. A. Carpenter, T. W. Darling, J. D. Bass, D. L. Lakshtanov, S. V. Sinogeikin and S. D. Jacobsen, “American Geophysical Union Fall Meeting,” 2006 (unpublished).
- X. Luo and B. Wang, “Structural and Elastic Properties of LaAlO3 from First-Principles Calculations,” Journal of Applied Physics, Vol. 104, No. 7, 2008, Article ID: 073518. doi:10.1063/1.2990068
NOTES
*Corresponding author.

