Advances in Materials Physics and Chemistry
Vol.2 No.4(2012), Article ID:26016,10 pages DOI:10.4236/ampc.2012.24036
In Silico Experiments of Carbon Dioxide Atmosphere and Buffer Type Effects on the Biomimetic Coating with Simulated Body Fluids
1State University of Rio de Janeiro, Nova Friburgo, Brazil
2Federal University of Rio de Janeiro, Rio de Janeiro, Brazil
Email: gmplatt@iprj.uerj.br
Received September 29, 2012; revised October 29, 2012; accepted November 14, 2012
Keywords: Hydroxyapatite; Thermodynamic Modelling; Carbon Dioxide, HEPES and TRIS Buffers; In Silico Experiments
ABSTRACT
The formation of calcium phosphate phases is extremely important in a biomedical engineering context. These phosphates are used in many applications, such as grafts, drug-delivery processes and evaluation of the bioactivity of metallic surfaces. Considering this scenario, it is useful to evaluate the thermodynamic conditions for the precipitation of phosphates of biomedical interest, mainly hydroxyapatite. In this work, we investigate the effects of two important factors using a thermodynamic framework: 1) carbon dioxide partial pressure; and 2) buffer type (2-Amino-2-hydroxymethyl-propane-1,3-diol, known as TRIS and 2-[4-(2-hydroxyethyl)piperazin-1-yl] ethanesulfonic acid, also called HEPES), on the driving force behind the precipitation of calcium phosphates in simulated body fluids. The in silico results show that the pH value is governed by carbon dioxide content, as expected to occur in vivo. Moreover, the buffers can deplete the free calcium available in solution and, consequently, can cause difficulties in the calcium phosphate precipitation.
1. Introduction
Hydrogen potential (pH) is a parameter of prime relevance in aqueous liquid phases, either with in vivo or in vitro situations. Therefore, species that are able to control their pH values deserve special attention in these systems. In the context of fluids that simulate those of body solutions, two chemicals are very important: carbon dioxide and buffers. In spite of this situation, few studies focus on the thermodynamic aspects of these chemicals in the precipitation of calcium phosphates.
Carbon dioxide partial pressure affects the pH of aqueous solutions and can promote an increase/decrease of carbonate/bicarbonate content in the liquid phase. Indeed, its partial pressure plays a key role in in vivo pH regulation.
The use of buffers is advisable in order to maintain the pH of aqueous systems within narrow ranges and, thus, several chemical reactions can take place under controlled physico-chemical conditions. However, besides protonation/deprotonation reactions of buffers, in some cases, several complexation reactions can occur, mainly with alkaline-earth ions. In these cases, the availability of specific ions is diminished, influencing all chemical equilibrium reactions, as well as the driving force to the precipitation of phosphate phases when these ions take part. In the specific case of calcium phosphates of biomedical interest, the quantity of free calcium ions in an aqueous system is extremely important because this parameter affects the stoichiometry of solid phases (such as hydroxyapatite). For example, using BISTRIS buffer, we noted a drastic depletion of calcium ion concentrations in simulated body fluids [1]. In the same context, Nakon and Krishnamoorthy [2] showed that, among 20 buffers known as “Good’s buffers”, three of them showed complexation reactions with metal ions, interfering particularly in protein analysis. In this paper, we analyze the depletion of calcium ions in the presence of TRIS buffer, comparing the results with HEPES buffer. Besides, the determination of the carbon dioxide effects on calcium phosphate precipitation was performed.
To evaluate the buffers and carbon dioxide in simulated body fluids, we choose a thermodynamic analysis, also known as in silico experiments, due to the scarcity of works that use a similar theoretical approach.
2. Models
2.1. Thermodynamic Models
In this subsection, we present the thermodynamic models employed in the in silico simulation of chemical equilibria of SBF fluids (essentially, multielectrolyte-diluted aqueous solutions).
Activity coefficients for charged species ( ) were calculated using long-range interactions. In this sense, we used the extended Debye-Hückel model [1] as follows:
) were calculated using long-range interactions. In this sense, we used the extended Debye-Hückel model [1] as follows:
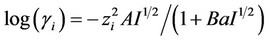 , (1)
, (1)
where  is the ionic radius,
is the ionic radius, 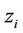 is the charge of chemical species i, I is the ionic force of medium and
is the charge of chemical species i, I is the ionic force of medium and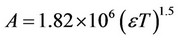 , where
, where 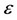 is the dielectric constant of water at 298.15 K and T is the absolute temperature (Kelvin). Also in (1), we considered the product
is the dielectric constant of water at 298.15 K and T is the absolute temperature (Kelvin). Also in (1), we considered the product 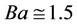 as suggested by Glinkina et al. [3] (BatesGuggenhein convention for chloride ions). This assumption is valid for ionic forces below 0.2 mol·L−1, as is the case for SBF solutions [4]. In this context, the ionic force is calculated by
as suggested by Glinkina et al. [3] (BatesGuggenhein convention for chloride ions). This assumption is valid for ionic forces below 0.2 mol·L−1, as is the case for SBF solutions [4]. In this context, the ionic force is calculated by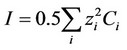 , where
, where 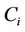 is the molar concentration (expressed in mol·L−1) of ion i.
is the molar concentration (expressed in mol·L−1) of ion i.
2.2. Chemical Equilibria and Material Balances
The numerical determination of concentrations—as well as activities and Gibbs free energy variations between supersaturated and saturated solutions—is conducted by a solution of a nonlinear algebraic system. This system contains chemical equilibrium relationships and material balances. We consider the following equilibrium reactions in aqueous solution.
a) Water formation/dissociation
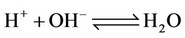 (2)
(2)
b) Protonation/deprotonation of phosphates
 (3)
(3)
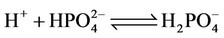 (4)
(4)
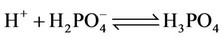 (5)
(5)
c) Calcium ion equilibria
 (6)
(6)
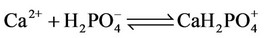 (7)
(7)
 (8)
(8)
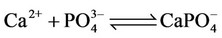 (9)
(9)
 (10)
(10)
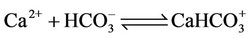 (11)
(11)
d) Carbonate/bicarbonate equilibrium
 (12)
(12)
e) Protonation/deprotonation of sulphates
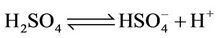 (13)
(13)
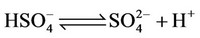 (14)
(14)
f) Magnesium ion equilibria
 (15)
(15)
 (16)
(16)
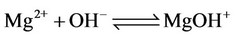 (17)
(17)
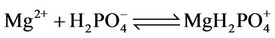 (18)
(18)
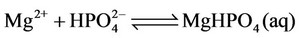 (19)
(19)
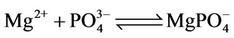 (20)
(20)
g) Protonation and complexation reactions of calcium and magnesium ions with buffers
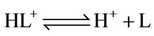 (21)
(21)
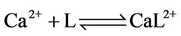 (22)
(22)
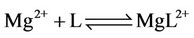 (23)
(23)
h) Reactions of carbon dioxide in aqueous medium
 (24)
(24)
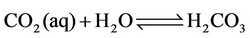 (25)
(25)
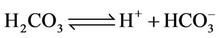 (26)
(26)
In these equations, L represents the buffer (TRIS or HEPES, in the present work), 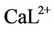 is the calciumbuffer complex and
is the calciumbuffer complex and  is the magnesium-buffer complex.
is the magnesium-buffer complex.
Besides chemical equilibrium equations, some material balances must be included. These balances are responsible for keeping the chemical content constant. In the following expression, the subscript TOT means the total quantity of a given element.
i) Material balance for phosphorous
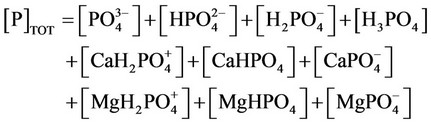 (27)
(27)
j) Material balance for inorganic carbon
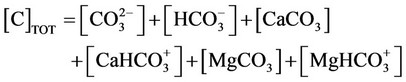 (28a)
(28a)
 (28b)
(28b)
k) Material balance for calcium
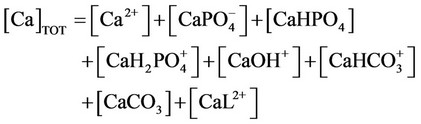 (29)
(29)
l) Material balance for magnesium
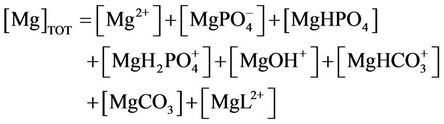 (30)
(30)
m) Material balance for sulfur
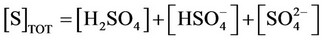 (31)
(31)
n) Material balance for buffer (TRIS or HEPES)
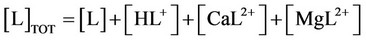 (32)
(32)
3. Degrees of Freedom Analysis
The system of nonlinear algebraic equations must be solved in order to access the concentrations of all chemical species (and, obviously, Gibbs free energies and supersaturations in the precipitation of calcium phosphates). The numerical resolution of equations depends on the necessary specification of the degrees of freedom in each approach. On the one hand, we consider a pH specification (in order to compare the effect of buffer type); on the other hand, a carbon dioxide partial pressure specification (to assess the resulting pH). Thus, the analysis of degrees of freedom for the nonlinear system is detailed for each case, here identified as Situation (a) (pH specification, buffer effect) and Situation (b) (carbon dioxide partial pressure specification, pH result). Situation (a) and (b) formulations were proposed by [1,5] and [6], respectively, for biomaterials applications; but, here, we present a unified approach for both situations and more detailed results/explanations concerning calcium phosphate precipitation.
3.1. Situation (a) (pH Specification, Buffer Effect)
The nonlinear system is formed by Equations (2)-(23), and by (27)-(32) (considering (28a)). Thus, we have 28 algebraic equations. The unknowns of this problem are:
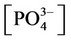 ,
,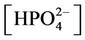 ,
,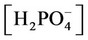 ,
,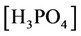 ,
,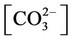 ,
,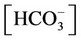 ,
,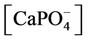 ,
,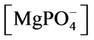 ,
,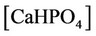 ,
,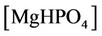 ,
,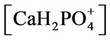 ,
,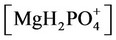 ,
,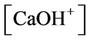 ,
,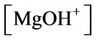 ,
,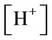 ,
,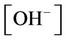 ,
,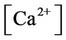 ,
,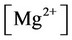 ,
,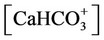 ,
,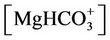 ,
,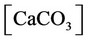 ,
, ,
,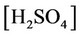 ,
,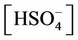 ,
,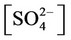 ,
,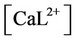 ,
,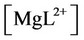 ,
,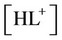 and
and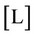 . Since we have 29 undetermined values for concentrations, one specification is necessary. If the pH value is available, the nonlinear system can be solved, and all concentrations are subsequently calculated. Table 1 shows degrees of freedom analysis for both cases.
. Since we have 29 undetermined values for concentrations, one specification is necessary. If the pH value is available, the nonlinear system can be solved, and all concentrations are subsequently calculated. Table 1 shows degrees of freedom analysis for both cases.
3.2. Situation (b) (Carbon Dioxide Partial Pressure Specification)
In this case, we must consider Equations (2)-(26) and (27)-(32) (using (28b)). Thus, this case considers 31 equations, with the same unknowns of case (a) plus 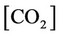 and
and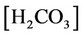 . Thus, with 31 unknowns and 31 equations, the degree of freedom is zero. However, the equilibrium relation of gaseous carbon dioxide and aqueous carbon dioxide (24) demands a value for partial pressure in the gaseous phase. This equilibrium can be calculated by the following expression [7]:
. Thus, with 31 unknowns and 31 equations, the degree of freedom is zero. However, the equilibrium relation of gaseous carbon dioxide and aqueous carbon dioxide (24) demands a value for partial pressure in the gaseous phase. This equilibrium can be calculated by the following expression [7]:
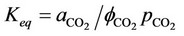 , (33)
, (33)
where  is the fugacity coefficient of carbon dioxide in gas phase and
is the fugacity coefficient of carbon dioxide in gas phase and 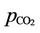 is the partial pressure of the same component in gas phase. Also in (33),
is the partial pressure of the same component in gas phase. Also in (33), 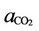 is the activity of carbon dioxide in liquid phase. The fugacity coefficient is evaluated by (33) from the reference [7]:
is the activity of carbon dioxide in liquid phase. The fugacity coefficient is evaluated by (33) from the reference [7]:
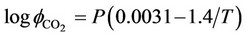 (34)
(34)
Table 1 presents the analysis of degrees of freedom for Situations (a) and (b), summarizing this information.
The nonlinear system representing Situation (a) or (b) is solved by a damped Newton method (in order to enhance convergence properties) [8].
4. Results and Discussion
In this section, we present some results concerning the effects of using buffers [Situation (a)] and the effect of carbon dioxide [Situation (b)] in simulated body fluids.
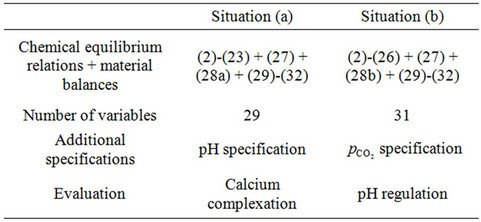
Table 1. Degrees of freedom analysis: Situations (a) and (b).
4.1. Situation (a)
We present some simulated results for a solution with the composition detailed in Table 2, for the TRIS and HEPES buffers. One can note that the concentrations shown in Table 2 do not correspond, for example, to the actual concentration of bicarbonate ion in solution, since we consider the carbonate/bicarbonate equilibrium in liquid phase. We also consider the same concentrations for both buffers in our simulated results. Equilibrium constants for the chemical reactions were presented in references [1,2] and [9-13]. There is an enormous quantity of works regarding to the measurements of formation constants for complexes in aqueous solutions involving calcium, magnesium, phosphates and sulfates at different temperatures and ionic forces. Therefore, in silico experiment previsions depend on the reliable values of these formation/dissociation constants.
Table 3 contains the equilibrium constants for the chemical reactions used in this work: the protonation/ deprotonation of buffers, and the complexation reactions of the calcium and magnesium ions. As far as we can see, HEPES buffer does not form complexes with calcium or magnesium when isolated (without ATP) and, therefore, these reactions were not considered in our results. Although out of scope of the present context,

Table 2.Total composition of solution [4,18].

Table 3. Equilibrium constants for protonation/deprotonation and complexation reactions (298.15 K) [9].
there is information about the complex Ca2+-HEPESATP and HEPES that act as an interferent in the amperometric determination of ATP (adenosinetriphosphate) in clinical applications [14]. Besides, HEPES buffer can form complexes with copper(II) ions in aqueous solutions [15-17]. Complexation constants for TRIS buffer are available in [9].
Figures 1 and 2 show, respectively, the concentration profiles for Ca2+ (free) and phosphate ions, as a function of pH for the TRIS and HEPES buffers. Clearly, we can observe that the concentration of free calcium ions is higher for HEPES buffer, because TRIS forms complexes with the calcium reducing its content in solution. At low pH, we noted an increase of free calcium ions. This situation seems to be favourable to hydroxyapatite formation, but we must consider that, at lower pH, the hydroxyapatite is not stable. Other interesting concentration profiles are related to phosphates in solution. It can be noted that phosphate ion concentration is very low in comparison with total phosphate (1.0 mmol·L−1, according to Table 2), as indicated in Figure 2. On the other hand, almost all phosphate appears as a complex with calcium ions (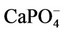 ), as shown in Figure 3. Just for a comparison with calcium ions, Figure 4 shows the concentration of
), as shown in Figure 3. Just for a comparison with calcium ions, Figure 4 shows the concentration of 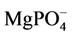 as a function of pH. The concentrations of
as a function of pH. The concentrations of 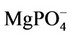 are not significant when compared tothe total magnesium concentration (1.5 mmol·L−1), but the concentrations of
are not significant when compared tothe total magnesium concentration (1.5 mmol·L−1), but the concentrations of 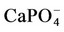 are relevant and can affect the driving force for hydroxyapatite precipitation. The high stability of this calcium phosphate complex in aqueous solutions was described by [10].
are relevant and can affect the driving force for hydroxyapatite precipitation. The high stability of this calcium phosphate complex in aqueous solutions was described by [10].
All the information presented and discussed previously can be condensed in other thermodynamic quantities, such as the Gibbs free energy variations for precipitation of calcium phosphates or supersaturations [4]. For instance, the Gibbs free energy variation between a supersaturated solution and the saturation condition (a driving force for the hydroxyapatite precipitation) is represented by [1]:
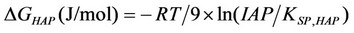 , (38)
, (38)
where IAP is the product of ionic activities (calculated from the solution of the nonlinear algebraic system that represents chemical equilibria and material balances, for situations (a) and (b)). The quantity 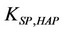 is the solubility constant product for hydroxyapatite at 298.15 K. The quantity R is the universal gas constant and T is the system temperature (Kelvin). A similar equation can be obtained by octacalcium phosphate.
is the solubility constant product for hydroxyapatite at 298.15 K. The quantity R is the universal gas constant and T is the system temperature (Kelvin). A similar equation can be obtained by octacalcium phosphate.
Figures 5 and 6 present the supersaturations of hydroxyapatite (HAP) and octacalcium phosphate (OCP) precipitations, respectively. An analysis of Figure 5 indicates that buffering with HEPES produces higher values for supersaturations, thereby, enhancing the driving
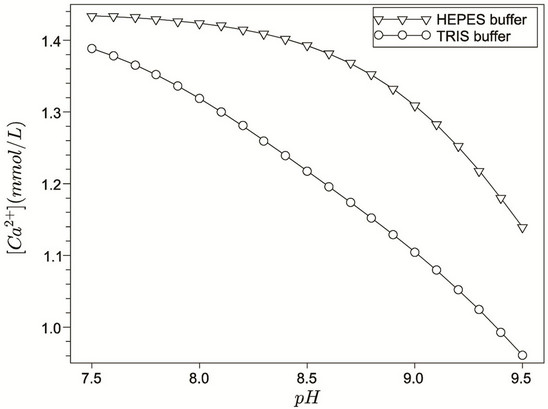
Figure 1. Concentration profiles for Ca2+ as a function of pH for the TRIS and HEPES buffers.
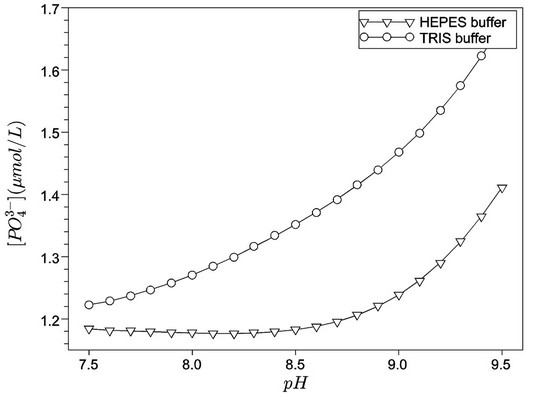
Figure 2. Concentration profiles for phosphate as a function of pH, for the TRIS and HEPES buffers.

Figure 3. Concentration profiles for as a function of pH, for the TRIS and HEPES buffers.
as a function of pH, for the TRIS and HEPES buffers.
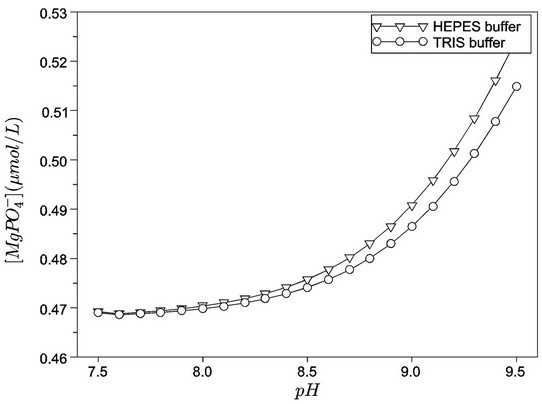
Figure 4. Concentration profiles for 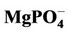 as a function of pH, for the TRIS and HEPES buffers.
as a function of pH, for the TRIS and HEPES buffers.

Figure 5. Supersaturation in hydroxyapatite precipitation, as a function of pH, for the TRIS and HEPES buffers.
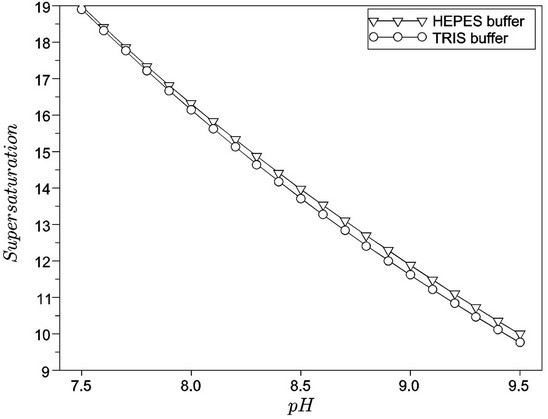
Figure 6. Supersaturation in octacalcium phosphate precipitation, as a function of pH, for the TRIS and HEPES buffers.
force for calcium phosphates precipitations. As expected—and also verified by in vitro and in vivo conditions—high pHs promote an increase in hydroxyapatite stability (verified by the increase in supersaturation); on the other hand, the octacalcium phosphate supersaturation decreases in the same scenario [19].
4.2. Situation (b)
For this problem, present in in vitro as well as in vivo situations, we used the same solution described in Table 1, but only with TRIS buffer. Clearly, in this aqueous system, a diminishing of the pH as a consequence of an increase of carbon dioxide partial pressure is observed. The partial pressures used in this work are compatible with the in vivo values. The equilibrium constant for Equation (24) was obtained from reference [7].
The calcium free concentration is important in the driving force for the phosphate precipitations (for hydroxyapatite, as previously discussed) and is presented in Figure 7. As expected, the calculations indicate that an increase of carbon dioxide partial pressure promotes an increase of free calcium concentration. Conversely, low pH values are not favourable for hydroxyapatite formation. Thus, there is a “trade-off” between these two quantities (pH and free calcium concentration).
Figures 8 and 9 show, respectively, the concentrations of carbonate and bicarbonate ions as functions of the partial pressure of carbon dioxide. As expected, an increase of 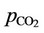 corresponds to a lower pH and, thus, carbonate concentrations tend to zero. Moreover, the concentration of bicarbonate ion presents a maximum value close to the
corresponds to a lower pH and, thus, carbonate concentrations tend to zero. Moreover, the concentration of bicarbonate ion presents a maximum value close to the 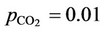 bar.
bar.
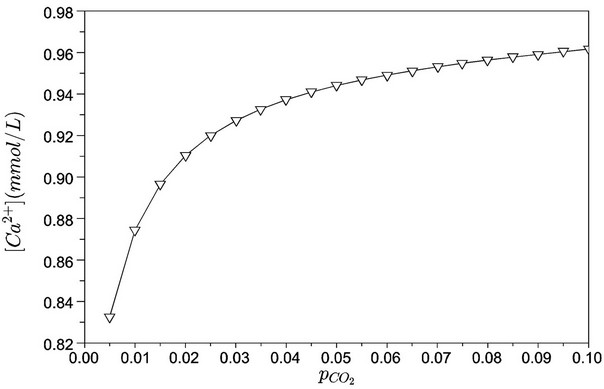
Figure 7. Free calcium concentration as a function of carbon dioxide partial pressure (bar).
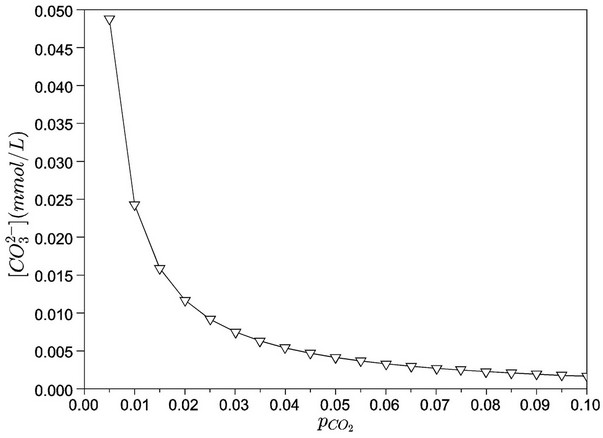
Figure 8. Carbonate concentration as a function of carbon dioxide partial pressure (bar).
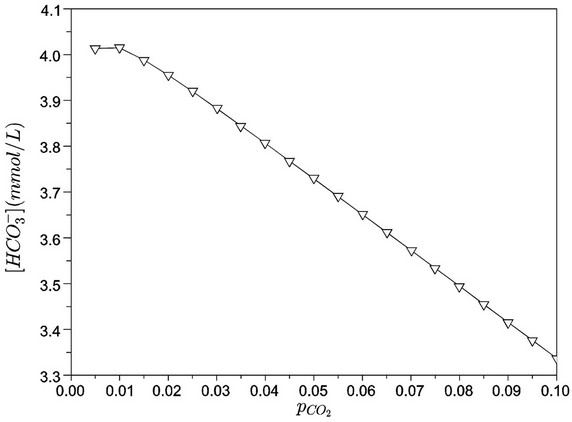
Figure 9. Bicarbonate concentration as a function of carbon dioxide partial pressure (bar).
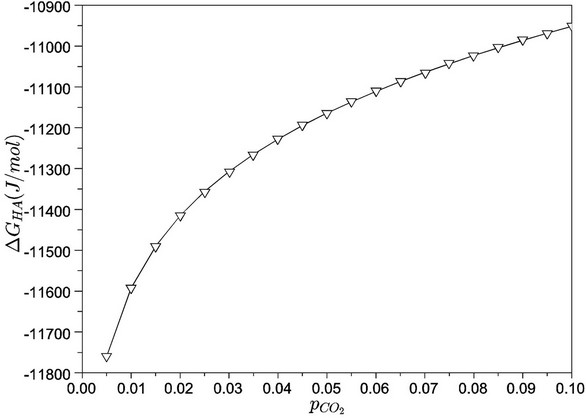
Figure 10. Gibbs free energies of hydroxyapatite precipitation, as a function of carbon dioxide partial pressure(bar).
Finally, Figure 10 presents the Gibbs free energy variations for hydroxyapatite precipitation, as functions of carbon dioxide partial pressures. As previously discussed, we noted a “trade-off” between the two most important quantities for hydroxyapatite formation: free calcium concentration and pH. However, the increase in free calcium availability—as indicated in Figure 7—is not capable of compensating for a lower pH due to the high carbon dioxide partial pressures. Indeed, we observed an increase in Gibbs free energies as consequences of high . This situation represents a less favourable condition for hydroxyapatite formation in the considered system. For higher pH (lower carbon dioxide partial pressures), we noted a significant increase in the thermodynamic driving force for hydroxyapatite precipitation. These results are fully compatible with experimental ones (see, for instance, [19]), which indicate a pH stability range for hydroxyapatite close to 9.5 - 12.0. This finding is only possible to achieve by numerical simulations due to the coupling of dozens of non-linear equations and chemical species present in simulated body fluids. Therefore, due to the typical (and high) non-linearity of equilibrium equations, the use of SBF with high concentration of chemicals generally does not give the expected proportionality results.
. This situation represents a less favourable condition for hydroxyapatite formation in the considered system. For higher pH (lower carbon dioxide partial pressures), we noted a significant increase in the thermodynamic driving force for hydroxyapatite precipitation. These results are fully compatible with experimental ones (see, for instance, [19]), which indicate a pH stability range for hydroxyapatite close to 9.5 - 12.0. This finding is only possible to achieve by numerical simulations due to the coupling of dozens of non-linear equations and chemical species present in simulated body fluids. Therefore, due to the typical (and high) non-linearity of equilibrium equations, the use of SBF with high concentration of chemicals generally does not give the expected proportionality results.
5. Conclusion
In this work, we investigated the influence of buffer types and carbon dioxide partial pressure (in the gaseous phase) in the chemical equilibrium of simulated body fluids. In addition, the driving force of hydroxyapatite formation, a calcium phosphate of great biomedical interest, was evaluated. We also presented a computational framework oriented to the solution of multielectrolyte chemical equilibria in this context, with different degrees of freedom and specifications. The main results indicated that: 1) HEPES buffer promotes a more favourable condition for hydroxyapatite/ octacalcium phosphate precipitation than TRIS buffer, since the first does not form complexes with calcium. These findings can be observed in supersaturation profiles for both buffers; 2) the considerations of a specified partial pressure of carbon dioxide (in gaseous phase) and other chemical equilibrium relations in aqueous phase have produced Gibbs free energy profiles of hydroxyapatite precipitation. At low partial pressures of carbon dioxide (high pH), hydroxyapatite is thermodynamically stable—compatible with experimental observations. An increase incarbon dioxide partial pressure reduces the driving force for hydroxyapatite precipitation. As an important remark, it is always advisable that equivalent in silico evaluation be performed before experimental works to know the effect of each chemical in the solution. Thus, in silico experiments are extremely useful tools for the design of simulated body fluids for different purposes.
6. Acknowledgements
G. M. Platt acknowledges the financial support of Fundação Carlos Chagas de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) and Coordenação de Aperfeiçoamento de Pessoal Superior (CAPES). I. N. Bastos, M. C. Andrade and G. D. Soares acknowledge the financial support of CNPq, CAPES and FAPERJ Brazilian agencies. G. M. Platt, I. N. Bastos and M. C. Andrade acknowledge UERJ for their ProCiencia Grants.
REFERENCES
- I. N. Bastos, G. M. Platt, M. C. Andrade and G. D. A. Soares, “Theoretical Study of Tris and Bistris Effects on Simulated Body Fluids,” Journal of Molecular Liquids, Vol. 139, No. 1-3, 2008, pp. 121-130. doi:10.1016/j.molliq.2007.12.003
- R. Nakon and C. R. Krishnamoorthy, “Free-Metal Ion Depletion by ‘Good’s’ Buffers,” Science, Vol. 221, No. 4612, 1983, pp. 749-750. doi:10.1126/science.6879173
- I. V. Glinkina, V. A. Durov and G. A. Mel’nitchenko, “Modelling of Electrolyte Mixtures with Application to Chemical Equilibria in Mixtures—Prototypes of Blood’s Plasma and Calcification of Soft Tissues,” Journal of Molecular Liquids, Vol. 110, No. 1-3, 2004, pp. 63-67. doi:10.1016/j.molliq.2003.09.001
- C. X. Resende, J. Dille, G. M. Platt, I. N. Bastos, G. A. Soares, “Characterization of Coating Produced on Titanium Surface by a Designed Solution Containing Calcium and Phosphate Ions,” Materials Chemistry & Physics, Vol. 109, No. 2-3, 2008, pp. 429-435. doi:10.1016/j.matchemphys.2007.12.011
- G. M. Platt, I. N. Bastos, M. C. Andrade and G. D. A. Soares, “Study of Buffer Effect on the Driving Force for the Precipitation of Calcium Phosphates with Biomedical Interest,” Proceedings of 6th Latin American Congress of Artificial Organs and Biomaterials, Gramado, 17-20 August 2010.
- G. M. Platt, I. N. Bastos, M. C. Andrade and G. D. A. Soares, “Phosphate Formation of Biomedical Interest in Carbon Dioxide Enriched Atmospheres,” Proceedings of 6th Latin American Congress of Artificial Organs and Biomaterials, Gramado, 17-20 August 2010.
- G. A. Zhang and Y. F. Cheng, “On the Fundamentals of Electrochemical Corrosion of X65 Steel in CO2-Containing Formation Water in the Presence of Acetic Acid in Petroleum Production,” Corrosion Science, Vol. 51, No. 1, 2009, pp. 87-94. doi:10.1016/j.corsci.2008.10.013
- C. T. Kelley, “Solving Nonlinear Equations with Newton’s Method,” SIAM, Philadelphia, 2003. doi:10.1137/1.9780898718898
- H. Sigel, K. H. Scheller and B. Prijs, “Metal-Ion/Buffer Interactions. Stability of Alkali and Alkaline Earth Ion Complexes with Triethanolamine (TEA), 2-Amino-2(hydroxymethyl)-1,3-propanediol (TRIS) and 2-[Bis(2-hydroxyethyl)-amino]2(hydroxymethyl)-1,3-propanediol (BISTRIS) in Aqueous and Mixed Solvents,” Inorganica Chimica Acta, Vol. 66, 1982, pp. 147-155. doi:10.1016/S0020-1693(00)85805-3
- A. Chugtai, R. Marshall and G. H. Nancollas, “Complexes in Calcium Phosphate Solutions,” Journal of Physical Chemistry, Vol. 72, No. 1, 1968, pp. 208-211. doi:10.1021/j100847a039
- T. E. Larson, F. W. Sollo Jr. and F. F. McGurk, “Complexes Affecting the Solubility of Calcium Carbonate in Water,” Research Report No. 68, University of Illinois at Urbana-Champaign, Urbana and Champaign, 1973.
- M. S. Tung, N. Eidelman, B. Sieck and W. E. Brown, “Octacalcium Phosphate Solubility Product from 4˚C to 37˚C,” Journal of Research of the National Bureau of Standards, Vol. 93, No. 5, 1988, pp. 613-624. doi:10.6028/jres.093.153
- P. W. Linder and J. C. Little, “Formation Constants for the Complexes of Orthophosphate with Magnesium and Hydrogen Ions,” Talanta, Vol. 32, No. 1, 1985, pp. 83-85. doi:10.1016/0039-9140(85)80027-8
- J. F. Masson, S. Gauda, B. Mizaikoff and C. Kranz, “The Interference of HEPES Buffer during Amperometric Detection of ATP in Clinical Applications,” Analytical Bioanalytical Chemistry, Vol. 390, No. 8, 2008, pp. 2067- 2071. doi:10.1007/s00216-008-2015-y
- M. Sokolowska and W. Bal, “Cu(II) Complexation by ‘Non-Coordinating’ N-2-hydroxyethylpiperazine-N-2-ethanesulfonic Acid (HEPES Buffer),” Journal of Inorganic Biochemistry, Vol. 99, No. 8, 2005, pp. 1653-1660. doi:10.1016/j.jinorgbio.2005.05.007
- M. T. S. D. Vasconcelos, M. A. G. O. Azenha and O. M. Lage, “Electrochemical Evidence of Surfactant Activity of the HEPES pH Buffer Which May Have Implications on Trace Metal Availability to Cultures in Vitro,” Analytical Biochemistry, Vol. 241, No. 2, 1996, pp. 248-253. doi:10.1006/abio.1996.0406
- K. Hegetschweiler and P. Saltman, “Interaction of Copper(II) with N-(2-hydroxyethyl)piperazine-N’-ethanesulfonic acid (HEPES),” Inorganic Chemistry, Vol. 25, No. 1, 1986, pp. 107-109. doi:10.1021/ic00221a028
- P. S. Vanzillotta, M. Sader, I. N. Bastos and G. A. Soares, “Improvement of in Vitro Titanium Bioactivity by Three Different Surface Treatments,” Dental Materials, Vol. 22, No. 3, 2006, pp. 275-282. doi:10.1016/j.dental.2005.03.012
- S. V. Dorozhkin, “Biocomposites and Hybrid Biomaterials Based on Calcium Orthophosphates,” Biomatter, Vol. 1, No. 1, 2011, pp. 3-56. doi:10.4161/biom.1.1.16782

