Theoretical Economics Letters
Vol.08 No.11(2018), Article ID:86429,14 pages
10.4236/tel.2018.811132
Measuring the Systemic Risk of Regional Banks in Japan with PLS-SEM
Necmi K. Avkiran
School of Business, The University of Queensland, St Lucia Campus, Australia
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 27, 2018; Accepted: July 30, 2018; Published: August 2, 2018
ABSTRACT
I embark to measure the systemic risk of regional banks in Japan through shadow banking (microlevel and macrolevel linkages) using partial least squares structural equation modeling (PLS-SEM). Non-parametric PLS-SEM is used for the first time in the context of Japanese banks. I collect indicator-based data from Orbis Bank Focus but do not find all the indicators suggested by theory. Results indicate systemic risk is explained by 12.5% of shadow banking. I use generalized structured component analysis (GSCA) for robustness test because it belongs to the same family of methods as PLS-SEM; PLS-SEM results are confirmed by GSCA. Regulators need to collect more data regarding shadow banking activities in relation to regional banks in Japan. The missing indicators are critical for explaining systemic risk in regional banks through shadow banking. Once more data are available, researchers can explore whether shadow banking has a substantial effect on the systemic risk of regional banks in Japan.
Keywords:
Systemic Risk, Shadow Banking, Regulated Banking, Regional Banks, Japan

1. Introduction
Japan’s financial crisis started in late 1990s and caused harm for capital and liquidity in its banking system. As a result, the economy fell into a deflationary state. Bank of Japan (BoJ) introduced zero interest rate policy in 1999 and then quantitative easing in March 2001 [1]. BoJ introduced its comprehensive monetary easing to alleviate deflationary pressures and slow recovery in October 2010. In April 2013, BoJ introduced further resources to monetary stimulus in terms of 2% price stability and large expansion of monetary base through buying of government securities.
However, the financial system was in trouble with negative yields and flat curves, raising fears about profitability. In September 2016, BoJ implemented yield curve control, monitoring short-term rates and long-term Japanese government bonds. In summary, more than a decade-long low level and volatility of government bonds’ yields produced interest rate risk and inadequate capital among financial institutions; this could lead to systemic risk. International Monetary Fund (IMF) recently highlighted the systemic risk in Japan’s banking system [2].
It is difficult to quantify systemic risk in integrated markets and it changes dynamically [3]. Reference [4] describes systemic risk as the clear hazard that difficulties with the operations of banks can be quickly shifted to others, including markets, and cause economic damage. Regulated banks are extremely leveraged institutions. The global financial crisis of 2007-2009 (GFC) exposed significant shortcomings of the existing regulation in terms of liquidity management, capital adequacy, and moral hazard. GFC encouraged extensive regulation in terms of macro linkages (market based) and micro linkages (firm based). At the micro level, Basel III requires banks to hold a minimum of 4.5% of core tier 1 equity against risk-weighted assets; regarding leverage ratio, Basel III sets a minimum of 3% (ratio of core tier 1 capital to consolidated but unweighted assets) [5] [6]. At the macro level, there is a capital surcharge on global systemic importance; this increases the core tier 1 capital between 1% - 2.5% of risk-weighted assets, i.e. Basel III requires a capital buffer that rises with firm size, complexity, interconnectedness and global importance.
For the first time in Japanese banking system, I use partial least squares structural equation modeling (PLS-SEM). PLS-SEM is iterative OLS regression, also known as PLS path modeling [7] [8]. PLS-SEM is a multivariate analysis method to estimate complex cause-effect relationships with latent variables. It has been used in various disciplines such as accounting [9] , finance [10] , management information systems [11] , marketing and strategic management [12] , operations management [13] , supply chain management [14] , and tourism [15]. The goal of the non-parametric PLS-SEM is to maximize the explained variance of endogenous latent construct(s) where the assumption of multivariate normality is relaxed. An introduction to PLS-SEM can be found in references [12] [16] [17] [18] , whereas reference [19] provides a step-by-step explanation of the mathematics behind its algorithm.
In the rest of the article, Section 2 covers the conceptual framework, Section 3 describes the data and method, Section 4 reports the results, Section 5 applies the robustness test, and Section 6 concludes.
2. Conceptual Framework
I focus on regional banks―the second largest group of banks in Japan (N = 64). Furthermore, the International Monetary Fund highlighted some vulnerabilities with regional banks [20] : 1) they need to raise their capital buffers, 2) stress tests show that credit-related losses represent the highest risk, and 3) vulnerabilities exist in foreign currency positions. Table 1 shows the list of regional banks.
I explain the consequences of systemic risk in the regulated banking sector (RBS) by microlevel and macrolevel linkages that can be traced to shadow banking (SB), e.g. market based financing through non-bank channels such as real estate investment trusts, leasing companies, credit guarantee outlets, money market funds, etc. Figure 1 identifies the general conceptual model. I use a set of indicators that are directly observable variables. I use PLS-SEM to understand the interconnectedness between shadow banking and regulated banking in terms of regional banks. As reference [10] state regarding PLS-SEM “Regulators need a method that is versatile, easy to use and can handle complex path models with latent variables”. As Basel III Accord better prepares banks for the next crisis (full implementation in 2019), regulators need to closely monitor the contribution of shadow banking to the regulated banking sector.
According to the regulatory arbitrage view, banks use special or structured investment vehicles (SIVs) [21] and special purpose vehicles (SPVs) to create interdependencies. Reference [22] reports that regulatory arbitrage is likely to
Table 1. The list of Japanese regional banks (N = 64).
Figure 1. General conceptual model explaining systemic risk using PLS-SEM.
increase as bank regulation becomes more strict (according to Basel III measures). As systemic risk increases, banks under distress lend less to clients (thus, clients invest less) and unemployment rises. This paper uses indicator-based approach that is favored by the Basel Committee and includes microprudential and macroprudential perspectives. Table 2 shows the potential indicators.
3. Data and Method
I work with end-of-financial year (i.e. 31 March 2017) data and I collect data from Orbis Bank Focus. Bank Focus is a database of banks worldwide; the information is sourced by Bureau van Dijk from a combination of annual reports, information providers and regulatory sources. Regarding data, not all the indicators in Table 2 are available. I replace formative indicators collateralized debt obligations (CDO) and collateralized loan obligations (CLO) with “total derivatives”; repurchase agreements and stock price are available. In terms of reflective indictors, capital ratio, non-interest income, non-performing loans and beta are available; modified BCBS score is not available. As a result, I collapse left-hand side of Figure 1 (shadow banking) into one exogenous construct. Due to some missing data, the new sample size is 45. Exhibit 1.7 in reference [18] recommends a sample size 37 for three independent variables (i.e. number of formative indicators), statistical power of 80%, significance level of 5% and minimum R-squared of 25%.
The distinction between formative and reflective indicators needs further explanation. Formative indicators are considered complementary. That is, a change in a given formative indicator can lead to a change in the associated latent construct. In multiple regression, the formative indicators are independent
Table 2. Ideal potential indicators for systemic risk.
aMACRO―macroprudential perspective; MICRO―microprudential perspective; SB―shadow banking.
variables. On the other hand, reflective indicators are treated as interchangeable because of the overlap among them. Thus, the endogenous latent construct depicted in Figure 1 becomes the independent variable in single regression runs, where the reflective indicators individually become dependent variables.
PLS-SEM models consist of three main components, namely, the structural or inner model, the measurement or outer models (see Figure 1), and the weighting scheme. A group of indicators (manifest variables) associated with a latent construct is referred to as a block, and an indicator can only be associated with one construct. I also note that PLS-SEM requires recursive models, i.e. there are no circular relationships or loops and the model is a causal chain [18] [24]. It is robust with skewed data because it transforms non-normal data according to the central limit theorem and it is considered an appropriate technique when working with small samples [18] [25]. Literature review in Table 1 in reference [17] identifies the top three reasons for choosing PLS-SEM as non-normal data, small sample size and presence of formative indicators.
The traditional covariance-based-SEM (CB-SEM) is able to model measurement error structures via a factor analytic approach but at the cost of covariances among the observed variables conforming to overlapping proportionality constraints, i.e. measurement errors are assumed to be uncorrelated [26]. CB-SEM assumes homogeneity in the observed population [27]. Such constraints are unlikely to hold unless latent variables are based on highly developed theory and the measurement instrument is refined through multiple stages. Thus, secondary data (non-experimental) frequently found in business databases are most unlikely to satisfy such constraints. In such cases, CB-SEM that relies on common factors would be inappropriate, and PLS-SEM that relies on weighted composites would be more appropriate because of its less restrictive assumptions. Furthermore, using formative indicators is problematic in CB-SEM because it gives rise to identification problems and reduces the ability of CB-SEM to reliably capture measurement error [28]. References [29] and [30] provide a highly readable discussion of advantages and disadvantages of CB-SEM versus PLS-SEM.
I identify PLS-SEM method under three models:
3.1. Reflective Measurement Model
Each reflective indicator is related to the endogenous construct or latent variable by a simple regression:
(1)
where is the hth regression where a reflective indicator is the dependent variable and p equals the number of reflective indicators, is the intercept, is the regression parameter to be estimated and ξ is the latent variable with a mean m and standard deviation of 1. The residual variable has a mean of zero and it is uncorrelated with the latent variable (known as the predictor specification condition, [24] ).
1) Internal consistency: According to references [12] [17] , composite reliability is a better measure of internal consistency because it avoids underestimation often seen with Cronbach’s alpha and accommodates differences in indicator reliabilities expected by PLS-SEM. A composite reliability of 0.6 is acceptable in exploratory research [12]. Composite reliability’s formula can be found in [18] , as well as in [29] , replicated below.
(2)
where , F, and are the factor loading, factor variance, and unique/error variance, respectively where i represents the indicator variable for a specific construct. Composite reliability is only relevant for the reflective measurement model.
2) Indicator reliability: Outer loadings greater than 0.7 are desirable [16]. Square of this standardized outer loading represents communality, that is, how much of the variation in the indicator is explained by the endogenous construct, and 1 minus communality reveals the measurement error variance. However, reference [12] state that in exploratory research, outer loadings as low as 0.4 are acceptable. Otherwise, if less than 0.4, the reflective indicator can be deleted.
3) Convergent validity: Average variance extracted (AVE) greater than 0.5 is preferred; this ratio implies that greater than 50% of the variance of the indicators have been accounted. AVE is only relevant for the reflective measurement model. When examining reflective indicator loadings, it is desirable to see higher loadings in a narrow range, indicating all items are explaining the underlying latent construct, i.e. convergent validity [29]. The formula for AVE is replicated below and it can be read in the context of Equation (2) above [29] :
(3)
4) Discriminant validity: Fornell-Larcker criterion needs to be satisfied. That is, the square root of AVE must be greater than the correlation of the construct with all other constructs; this criterion is not applicable to formative measurement models and single-item constructs.
3.2. Formative Measurement Model
Under the formative measurement model, it is assumed that the exogenous construct (latent variable, ) is defined by the formative indicators that could be multidimensional and a residual term found in a linear function.
(4)
where is the weight, the residual vector δ has a mean of zero and it is uncorrelated with the formative indicators where h captures the range of formative indicators [24].
1) Convergent validity: Higher path coefficients linking the exogenous and endogenous constructs are preferred, implying adequate coverage by the formative indicators [29]. A substantial coefficient of determination (R2) is also a good indication of convergent validity.
2) Multi-collinearity among indicators: When multi-collinearity exists, standard errors and thus variances are inflated. A variance inflation factor (VIF) is calculated for each of the explanatory variables in OLS regression, and VIF must be less than 5 [16] , i.e. VIF represents the factor by which variance is inflated.
(5)
where is the proportion of variance of formative indicator i associated with other indicators in the same block [18]. Statistically, VIF is the reciprocal of tolerance, , where the latter is defined as the variance of a formative indicator not explained by others in the same block. A VIF of 1 means there is no correlation among the predictor variable examined and the rest of the predictors, and therefore, the variance is not inflated.
3) Significance and relevance of outer weights: “Weight” is an indicator’s relative contribution; “loading” is an indicator’s absolute contribution. One can start with bootstrapping using 5000 sub-samples [16] in order to check whether outer weights are significantly different from zero. Bootstrapping involves random drawing of sub-samples from the original set of data with replacement (sub-sample size equals the original sample size). Indicators with significant outer weights are kept; otherwise, an indicator can still be kept if its outer loading, that is, its absolute contribution is greater than 0.5. Insignificant formative indicators based on p-values (i.e. higher than 5%) with outer loadings less than 0.5 can be removed from the model for being irrelevant.
3.3. Structural Model
I emphasize that if the outer models, that is, measurement models are not reliable, little confidence can be held in the inner (structural) model. Analysis of the structural model is an attempt to find evidence supporting the theoretical model, i.e. the theorized relationships between exogenous constructs and the endogenous construct.
(6)
where is the endogenous construct (in this study there is one endogenous construct, therefore j equals 1) and represents the exogenous constructs (i equals 2); the predictor specification condition applies [24].
1) Predictive accuracy, coefficient of determination (R2): This statistic indicates to what extent the exogenous construct(s) are explaining the endogenous construct. According to references [18] [16] , 0.25 (weak), 0.50 (moderate) and 0.75 (substantial). However, unless the adjusted R2 is used (for a formal definition, see [18] ), this coefficient can be upward-biased in complex models where more paths are pointing towards the endogenous construct.
2) Predictive relevance (Q2): This statistic is obtained by the sample re-use technique called ‘Blindfolding’ where omission distance is set between 5 - 10, where the number of observations divided by the omission distance is not an integer [12]. For example, if you select an omission distance of 7, then every seventh data point is omitted and parameters are estimated with the remaining data points. According to reference [18] , omitted data points are considered missing values and replaced by mean values. Estimated parameters help predict the omitted data points and the difference between the actual omitted data points and predicted data points becomes the input to calculation of Q2. Blindfolding is applied only to endogenous constructs with reflective indicators. If Q2 is larger than zero, it is indicative of the path model’s predictive relevance in the context of the endogenous construct and the corresponding reflective indicators. The formula follows [28] :
(7)
where D is the omission distance in blindfolding, E is the sum of squares of prediction error, and O is the sum of squares errors using the mean for prediction.
3) Significance of path coefficients: Bootstrapping is needed, following which p-values for the path coefficients are checked.
4. Results
In this section, I report the results under three models using PLS-SEM. I use Smart PLS software [31].
4.1. Reflective Measurement Model
1) Internal consistency: Composite reliability is lower than 0.6 at 0.420, casting some doubt on internal consistency of the reflective measurement model.
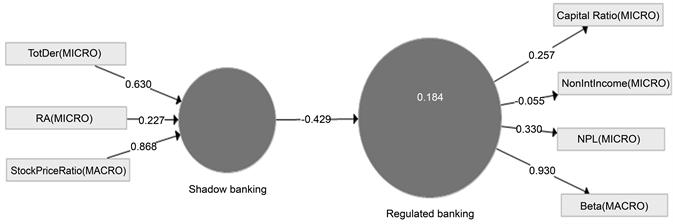
2) Indicator reliability: The highest outer loadings belongs to beta (0.930), followed by non-performing loans (0.330), capital ratio (0.257) and non-interest income (−0.055) (see Figure 2).
3) Convergent validity: AVE equals 0.261, below the preferred minimum of 0.5, suggesting less than 50% of the variance of the reflective indicators have been accounted by the latent endogenous construct.
4) Discriminant validity: The square root of AVE (0.511) must be greater than the correlation of the construct with all other constructs. Fornell-Larcker criterion is satisfied.
4.2. Formative Measurement Model
1) Convergent validity: The path coefficient is −0.429 from the shadow banking to the regulated banking (see Figure 2). R2 stands at 18.4%, or 16.5% adjusted.
2) Multi-collinearity among indicators: Outer VIF values range between 1.039 - 1.227 and are substantially under 5, indicating absence of multi-collinearity and inflated variance.
3) Significance and relevance of outer weights: Eliminating formative indicators should be approached with caution because formative measurement theory expects the indicators to cover the domain of a construct, i.e. formative indicators are complementary. Since I have three formative indicators, I do not delete any.
Figure 2. PLS-SEM first run. Legend Formative indicators: TotDer: total derivatives; RA: repurchase agreements; StockPriceRatio: the ratio of a bank’s stock price to the banking sector stock index; Reflective indicators: Capital Ratio: total regulatory capital ratio; NonIntIncome: non-interest income scaled by interest income; NPL: non-performing loans scaled by total loans; Beta: financial beta defined as volatility of bank share price relative to the overall stock market.
4.3. Structural Model
1) Predictive accuracy, coefficient of determination (R2): The adjusted R2 is 16.5% and is weak according to the general guidelines.
2) Predictive relevance (Q2): Q2 is smaller than zero at −0.045, suggesting problems with the reflective indicators.
3) Significance of path coefficients: P-value for path coefficient is 0.387 between the shadow banking and regulated banking, indicating insignificance.
I proceed to the second run. The reflective indicators non-interest income and capital ratio should be deleted because outer loadings are low. I proceed without these indicators and report new results (see Figure 3). Composite reliability rises from 0.420 to 0.664 (above the minimum 0.6). AVE rises from 0.261 to 0.540 (above the minimum 0.5), and following bootstrapping, p-value for path coefficient is in now 0.078 (instead of 0.387). Blindfolding leads to a healthy Q2 of 0.020. Adjusted R2drops to 12.5% because of fewer indicators.
5. Robustness Test
References [32] [33] introduced generalized structured component analysis (GSCA) as an alternative to PLS-SEM. I apply GSCA as a robustness test because it belongs to the same family of methods. PLS-SEM and GSCA are both variance-based methods, appropriate for predictive modeling. GSCA uses a global optimization function in parameter estimation with least squares [34]. CB-SEM is not a meaningful alternative to PLS-SEM under the conditions of the current study where the sample size is small, formative indicators are present, and the study is exploratory rather than confirmatory.
GSCA maximizes the average or the sum of explained variances of linear composites, where latent variables are determined as weighted components or composites of observed variables. GSCA follows a global least squares optimization criterion and it is minimized to generate the model parameter estimates. GSCA is not scale-invariant and it standardizes data. GSCA retains the advantages of PLS-SEM, such as fewer restrictions on distributional assumptions, unique component score estimates, and avoidance of improper solutions with small samples [32] [34].
I use the web-based GSCA software GeSCA (http://www.sem-gesca.org/) for robustness testing of the reduced model. In Table 3, the PLS-SEM results are
Table 3. Robustness testing of PLS-SEM with GSCA.
Figure 3. PLS-SEM second run (reduced model). Legend Formative indicators: TotDer: total derivatives; RA: repurchase agreements; StockPriceRatio: the ratio of a bank’s stock price to the banking sector stock index; Reflective indicators: NPL: non-performing loans scaled by total loans; Beta: financial beta defined as volatility of bank share price relative to the overall stock market.
confirmed by GSCA; all the figures are similar with the exception of non-performing loans.
6. Concluding Remarks
I measure the systemic risk of regional banks in Japan using partial least squares structural equation modeling. First run has problems. After I delete the reflective indicators, non-interest income and capital ratio, composite reliability and AVE improves; following bootstrapping, p-value improves. Blindfolding leads to healthy Q2.
As I delete two reflective indicators, the statistics in PLS-SEM improve substantially. Unfortunately, the few available formative indicators with regional banks of Japan do not result in high R2. The shadow banking explains the systemic risk in regulated banking (regional banks) to the tune of 12.5% (adjusted R2). Regulators need to collect more data based on Table 2 and beyond. After more data collection, researchers can explore if shadow banking has a high impact on regional banks in Japan in terms of systemic risk.
Regarding the indicators listed in Table 2, I used Orbis Bank Focus database. On the formative indicators side, I could not identify collateralized debt obligations or collateralized loan obligations; proxy for these two variables was total gross exposure under derivatives. I could not locate number of shadow banking facilities in offshore financial centres, nor number of associations with structured credit vehicles. On the reflective indicators side, the only variable I could not find was modified Basel Committee on Banking Supervision score. I am not surprised that the adjusted R2 was 12.5% with reduced indicators but this number indicated an impact on systemic risk of regional banks due to shadow banking. The missing variables are critical for explaining systemic risk in regional banks through shadow banking. Further research can be undertaken to confirm the effect of shadow banking on the systemic risk of regional banks once more data are available.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Avkiran, N.K. (2018) Measuring the Systemic Risk of Regional Banks in Japan with PLS-SEM. Theoretical Economics Letters, 8, 2024-2037. https://doi.org/10.4236/tel.2018.811132
References
- 1. Systemic Risk and Systematic Value (2017) http://www.sr-sv.com/non-conventional-monetary-policy/bank-of-japan/
- 2. International Monetary Fund (2017) https://www.japantimes.co.jp/news/2017/10/12/business/imf-highlights-risk-systemic-stress-japans-banking-system/#.WgPS3aKGfAU
- 3. Calluzzo, P. and Dong, G.N. (2015) Has the Financial System Become Safer after the Crisis? The Changing Nature of Financial Institution Risk. Journal of Banking and Finance, 53, 233-248. https://doi.org/10.1016/j.jbankfin.2014.10.009
- 4. Gart, A. (1994) Regulation, Deregulation, Reregulation: The Future of the Banking, Insurance, and Securities Industries. John Wiley & Sons, New York.
- 5. Basel Committee on Banking Supervision (2011) Basel III: A Global Regulatory Framework for Moreresilient Banks and Banking Systems. Bank for International Settlements (June).
- 6. Basel Committee on Banking Supervision (2011) Global Systemically Important Banks: Assessment Methodology and the Additional Loss Absorbency Requirement: Rules Text. Bank for International Settlements (November).
- 7. Wold, H.O.A. (1982) Soft Modeling: The Basic Design and Some Extensions. In: Joreskog, K.G. and Wold, H.O.A., Eds., Systems under Indirect Observations: Part II, North-Holland, Amsterdam, 1-54.
- 8. Lohmoller, J.B. (1989) Latent Variable Path Modeling with Partial Least Squares. Physica-Verlag, Heidelberg. https://doi.org/10.1007/978-3-642-52512-4
- 9. Lee, L., Petter, S., Fayard, D. and Robinson, S. (2011) On the Use of Partial Least Squares Path Modeling in Accounting Research. International Journal of Accounting Information Systems, 12, 305-328. https://doi.org/10.1016/j.accinf.2011.05.002
- 10. Avkiran, N.K., Ringle, C.M. and Low, R. (2018) Monitoring Transmission of Systemic Risk: Application of PLS-SEM in Financial Stress Testing. The Journal of Risk, 20, 83-115. https://doi.org/10.21314/JOR.2018.386
- 11. Ringle, C.M., Sarstedt, M. and Straub, D.W. (2012) A Critical Look at the Use of PLS-SEM in MIS Quarterly. MIS Quarterly, 36, iii-xiv.
- 12. Hair, J.F., Sarstedt, M., Ringle, C.M. and Mena, J.A. (2012) An Assessment of the Use of Partial Least Squares Structural Equation Modeling in Marketing Research. Journal of the Academy of Marketing Science, 40, 414-433. https://doi.org/10.1007/s11747-011-0261-6
- 13. Peng, D.X. and Lai, F. (2012) Using Partial Least Squares in Operations Management Research: A Practical Guideline and Summary of Past Research. Journal of Operations Management, 30, 467-480. https://doi.org/10.1016/j.jom.2012.06.002
- 14. Kaufmann, L. and Gaeckler, J. (2015) A Structured Review of Partial Least Squares in Supply Chain Management Research. Journal of Purchasing and Supply Management, 21, 259-272. https://doi.org/10.1016/j.pursup.2015.04.005
- 15. do Valle, P.O. and Assaker, G. (2016) Using Partial Least Squares Structural Equation Modeling in Tourism Research: A Review of Past Research and Recommendations for Future Applications. Journal of Travel Research, 55, 695-708. https://doi.org/10.1177/0047287515569779
- 16. Hair, J.F., Ringle, C.M. and Sarstedt, M. (2011) PLS-SEM: Indeed a Silver Bullet. Journal of Marketing Theory and Practice, 19, 139-151. https://doi.org/10.2753/MTP1069-6679190202
- 17. Hair, J.F., Sarstedt, M., Hopkins, L. and Kuppelwieser, V.G. (2014) Partial Least Squares Structural Equation Modeling (PLS-SEM): An Emerging Tool in Business Research. European Business Review, 26, 106-121. https://doi.org/10.1108/EBR-10-2013-0128
- 18. Hair, J.F., Hult, G.T.M., Ringle, C.M. and Sarstedt, M. (2017) A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM). 2nd Edition, Sage Publications, Inc., Thousand Oaks.
- 19. Monecke, A. and Leisch, F. (2012) semPLS: Structural Equation Modeling Using Partial Least Squares. Journal of Statistical Software, 48, 1-32. https://doi.org/10.18637/jss.v048.i03
- 20. International Monetary Fund (2017) Japan: Financial Sector Assessment Program. IMF Country Report No. 17/285 (September).
- 21. Gennaioli, N., Shleifer, A. and Vishny, R.W. (2013) A Model of Shadow Banking. The Journal of Finance, 68, 1331-1363. https://doi.org/10.1111/jofi.12031
- 22. Financial Stability Board (2011) Shadow Banking: Scoping the Issues. A Background Note of the Financial Stability Board.
- 23. Institute for Monetary and Economic Studies (2014) A Survey of Systemic Risk Measures: Methodology and Application to the Japanese Market. Discussion Paper No. 2014-E-3, Bank of Japan.
- 24. Tenenhaus, M., Vinzi, V.E., Chatelin, Y.-M. and Lauro, C. (2005) PLS Path Modeling. Computational Statistics & Data Analysis, 48, 159-205. https://doi.org/10.1016/j.csda.2004.03.005
- 25. Henseler, J., Ringle, C.M. and Sinkovics, R.R. (2009) The Use of Partial Least Squares Path Modeling in International Marketing; New Challenges to International Marketing. Advances in International Marketing, 20, 277-319. https://doi.org/10.1108/S1474-7979(2009)0000020014
- 26. Joreskog, K.G. (1979) Basic Ideas of Factor and Component Analysis. In: Joreskog, K.G. and Sorbom, D. Eds., Advances in Factor Analysis and Structural Equation Models, University Press of America, New York, 5-20.
- 27. Wu, W.W., Lan, L.W. and Lee, Y.T. (2012) Exploring the Critical Pillars and Causal Relations within the NRI: An Innovative Approach. European Journal of Operational Research, 218, 230-238. https://doi.org/10.1016/j.ejor.2011.10.013
- 28. Petter, S., Straub, D.W. and Rai, A. (2007) Specifying Formative Constructs in Information Systems Research. MIS Quarterly, 31, 623-656. https://doi.org/10.2307/25148814
- 29. Chin, W.W. (2010) How to Write Up and Report PLS Analyses. In: Esposito Vinzi, V., Chin, W.W., Henseler, J. and Wang, H., Eds., Handbook of Partial Least Squares: Concepts, Methods and Applications, Springer Handbooks of Computational Statistics Series, Vol. II, Springer, Heidelberg, Dordrecht, London, New York, 655-690. https://doi.org/10.1007/978-3-540-32827-8_29
- 30. Sarstedt, M., Hair, J.F., Ringle, C.M., Thiele, K.O. and Gudergan, S.P. (2016) Estimation Issues with PLS and CBSEM: Where the Bias Lies! Journal of Business Research, 69, 3998-4010. https://doi.org/10.1016/j.jbusres.2016.06.007
- 31. Ringle, C.M., Wende, S. and Becker, J.M. (2015) SmartPLS 3. SmartPLS GmbH, Bonningstedt.
- 32. Hwang, H. and Takane, Y. (2004) Generalized Structured Component Analysis. Psychometrika, 69, 81-99. https://doi.org/10.1007/BF02295841
- 33. Hwang, H. and Takane, Y. (2014) Generalized Structured Component Analysis: A Component-Based Approach to Structural Equation Modeling. Chapman & Hall, New York. https://doi.org/10.1201/b17872
- 34. Hwang, H., Ho, M.-H. and Lee, J. (2010) Generalized Structured Component Analysis with Latent Interactions. Psychometrika, 75, 228-242. https://doi.org/10.1007/s11336-010-9157-5