Received 25 November 2015; accepted 20 December 2015; published 23 December 2015

ABSTRACT

We model the competition between a proprietary firm and an open source rival, by incorporating the nature of the GPL, investment opportunities by the proprietary firm, user-developers who can invest in the open source development, and a ladder type technology. We use a two-period dynamic mixed duopoly model, in which a profit-maximizing proprietary firm competes with a rival, the open source firm, which prices the product at zero, with the quality levels determining their relative positions over time. We analyze how the existence of open source firm affects the investment and the pricing behavior of the proprietary firm. We also study the welfare implications of the existence of the open source rival. We find that, under some conditions, the existence of an open source rival may decrease the total welfare.

Keywords:

Open Source Innovation, GPL, Research and Development, Dynamic Games

1. Introduction

Software is called open source, if its source code is open in the sense that anyone has free access to it. Open source movement aims to bring programmers not concerned with proprietary ownership or any financial gain together to produce a more useful and bug-free product for everyone to use. By revealing its source code, an open source can be refined by many independent developers all around the world. The source code of an open source product is made available free of charge to the public. So, the user-developers read, redistribute and modify the source code, generating an advantageous evolution of it.

Among many licenses that are used to distribute open source projects, GNU General Public License (GPL) is the most commonly used one as of late 2014, by a share above 51%¹. Under GPL, every user has the right to use and modify the code freely, but the modifications must be distributed under the terms of the same license, if they are to be distributed at all. Also, GPL allows for the commercial exploitation of the program. Hence, the users have to sustain the free access to the source code; yet, as long as they maintain the free access, they are allowed to make profits².

The success of open source software has generated a literature on it, which has been flourishing since early 2000s. Lerner and Tirole (2002, 2005) [1] [2] introduce a broad discussion on economics of open source development. They indicate two reasons that might lead the developers to contribute to open source evolution. First reason that might make developers involve in this costly activity is that they receive a direct benefit in the form of improved software. Secondly, they get an indirect benefit by signaling their abilities in the job market. They also point out that the literature mostly considers individual incentives to adopt open source software. Johnson (2002) [3] uses public good approach in a static environment, where private provision of user-developers to a public good―the open source―diminishes as the number of user-developers increases because of free riding problem, and presents some comparative statistics and welfare results. Modica (2012) [4] takes a two-period oligopoly game using a circular city approach in order to model the open source innovations from a public good perspective. Some of the open source literature focuses on the competition between proprietary firm and open source firm. Casadesus-Masanell and Ghemawat (2006) [5] study the competition between proprietary firm and open source firm in a dynamic mixed duopolostic industry with the demand side learning, and show that it is better to have the proprietary firm as a monopoly when the total welfare is considered. Casadesus-Masanell and Llanes (2011) [6] use a mixed duopoly structure, where a for-profit proprietary firm competes with an open source firm, which tries to maximize the value of its open software. Our model differs from these studies in the way that it combines the open source innovation and the competition between proprietary firm and open source firm in a dynamic environment, and incorporates the features of GPL licensing³.

We examine the effects of the existence of an open source firm that is competing with the proprietary firm on the proprietary firm’s investment in innovation and production behavior, and how it affects the total welfare in the market. We set up a dynamic model with two periods, the first of which has two stages: competition and investment. In the second period, there is only price competition. In the two competition stages, proprietary firm and open source firm compete in a mixed duopolistic industry, where the former charges a price to maximize its overall expected profit, whereas, the latter is freely available. At the beginning of each period, a new cohort of potential users enters into the model. At the beginning of the competition stage, they observe the quality levels and the price of proprietary firm’s product, and they decide which operating system to use during their life time of one period. In the next stage of the first period, the investment stage, while proprietary firm invests in probability to increase its products quality level, user-developers’ incentives for involving this costly development activity is to signal their abilities.

We find that under some circumstances, the proprietary firm supplies less and invests more in the presence of the open source rival, which leads the proprietary firm to make less profit in the duopolistic industry compared to its monopoly, suggesting that a duopoly is likely to dominate the proprietary firm’s monopoly in terms of total welfare generation. However, this is not always true, that is, it might be better for the total welfare when there is only proprietary firm in the market, and no open source rival.

2. The Model

We consider a mixed duopoly model, where there are two firms, each providing an operating system, one of which is proprietary and the other is open source⁴. There are two periods. The first period has two stages, competition and investment. In the second period there is only competition. The quality level of an operating system, at the beginning of period t, is denoted as, where w stands for Windows and 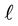stands for

Linux. Here, 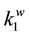and 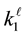are given, but 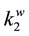and will be determined endogenously by the investment decisions of Windows and Linux user-developers, respectively.

The evolution of quality levels follow a ladder type technology and investments are in the form of success probability. If Windows invests at, its quality level at the beginning of 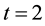will be:

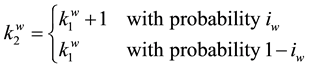
Linux user-developers also invest in probability of success and those who are successful get an exogenous bonus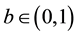. If at least one user developer succeeds in development stage, because of the terms of GPL, Linux will move up one step in the technology ladder, and will stay at current step otherwise. Let 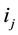denote the user-developer j’s investment level. Then, Linux’ quality level at the beginning of the second period will be:

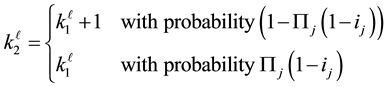
Cost of investment i is, for both Linux user-developers and Windows. At the beginning of each

period, Windows announces a price of. In each period, a new cohort of N potential users enter into the market. They observe the quality levels of both Windows and Linux. Let denote the quality differences between Windows and Linux,. Let denote the value attached to the operating system s by the cohort entering at time t. Let be the number of users in period t, who buy Windows, then is the number of Linux user-developers in the same period since Linux is freely available.

Assumption 1. (Linear Demand) In period t, for, the value of Windows to a user is and the value of Linux to is.

Assumption 2. for. is increasing and is decreasing in ⁵.

Assumption 3. is concave in ⁶.

Timing of Events: At, Windows has a quality level and Linux has. There are N buyers who live for one period only. Windows announces its price. Buyers choose either Windows at or Linux at zero price. Windows invests, and each Linux user-developer j invests. The success/failure outcomes, thus new quality levels, are realized. At, a new cohort of N buyers enter. Windows announces its price and buyers choose either Windows at or Linux at zero price. Profits are realized.

3. Benchmark: No Open Source, Windows Is Monopoly

In a market, where there is no substitute for Windows, and every user of any cohort has positive willingness to

pay, inverse demand function is directly obtained by. We use backward induction.

SECOND PERIOD

Since Windows is the only operating system producer and this is last period of the game, having monopoly power, it produces the profit maximizing amount of, and sets its price to in accordance with

the demand structure. As a result, it generates a profit of:.

FIRST PERIOD: Investment

An investment level will increase its quality level by 1 with the probability. Given the second period profit level, Windows chooses an investment level, which is

Since the above term is linear in, the monopoly investment level will be:

(1)

FIRST PERIOD: Monopoly Price

Windows chooses a price level, , or equivalently, quantity level, , that maximizes its following overall expected profit:

which has the unique solution and.

4. Equilibrium in the Duopoly

Since Linux can be acquired freely and, it is guaranteed that every user will get one operating system, at least Linux. Hence, at period t, if is the number of users who buy Windows, then the remaining users of cohort t, , obtain the Linux at no price, and they become Linux user-developers.

SECOND PERIOD

When Windows’ price is at period 2, the indifferent user between Windows and Linux, , is found by the following equation:

Using, the inverse demand function for Windows in period 2 is

(2)

Windows, a profit maximizer, produces such that

Taking the first order derivative with respect to, we get quantity and price levels for the second period as follows: and ⁷. Thus, the profit level in the second period is.

FIRST PERIOD: Linux user-developers’ investment decisions

In the investment stage, the actions of the user-developers have impact on Windows’ objectives. However, Windows’ investment decision does not affect the user-developers’ investment strategies since they invest only for the purpose of signaling their job skills. This is captured through, b, a bonus, which a successful user-developer receives. Thus, a user-developer, chooses and investment level, which solves the following maximization problem

where the solution is. Hence, her expected net benefit, , is positive, in the equilibrium. Due to the

symmetry, for all. Thus, Linux will be developed with probability, which is the probability that at least one user-developer succeeds.

FIRST PERIOD: Windows’ investment decisions

Windows chooses the investment level, which solves

First order condition implies,

which is equivalent to, where and .

FIRST PERIOD: Price competition

In the equilibrium, choosing to get Linux for free ensures a user to get an expected benefit of in the in-

vestment stage. Then, when Windows is sold at price at, the indifferent user between Windows and Linux, , is found by the following equation:

Thus, the inverse demand for Windows in at is

(3)

Windows maximizes its expected profit choosing:

The first order condition is

Now, we compare the first period quantities of Windows for the cases where it’s a monopoly and where it competes with Linux.

Proposition 1. For large enough bonus b, proprietary firm produces less in the first period of the duopolistic competition relative to the case in which it is a monopoly.

Proof. Define, which is the above first order condition of the Windows’ first period price choice problem, evaluated at. Note that

is continuous in, , and. Therefore, such that,. Because the first order condition is negative at point for large b’s and, the overall ex-

pected profit function is concave in, we get. □

Proposition 1 shows that the existence of an open source rival reduces the firm’s quantity, which is not surprising. Now, we compare the investment decisions of Windows in cases of a monopoly and existence of open source rival.

Proposition 2. Proprietary firm makes more investment in the duopoly industry competition as opposed to the case where it is a monopoly.

Proof. Let. Observe that. Since is concave, is negative, and is positive. Hence,

which implies. □

Proposition 2 shows that competition results in Windows to increase its investment level.

5. Welfare Comparison

Proposition 1 & 2 concludes that the proprietary firm makes less profit in the duopoly industry, which suggests that a duopoly is likely to dominate proprietary firm’s monopoly in terms of total welfare generation. In this section, we analyze the welfare implications of the two industry structure that we studied above. Instead of finding the absolute level of total welfare in the duopoly industry, we will compare the total welfare levels under the assumptions that and are linear with slope and, respectively⁸.

Proposition 3. If and, then total welfare is higher in proprietary firm’s monopoly than the total welfare in duopoly industry.

Proof. We divide the total welfare into pieces and compare them piece-wise. When comparing the two welfare levels, we interpret the absence of Linux in the monopoly as and being zero, that is,. Expected total welfare in the Windows’ monopoly, is

Expected welfare in the first period of the duopoly industry,:

And the expected total welfare generated in the second period of the duopoly will be:

Equivalently,

Now, we compare the pieces marked by lower case letters. For,. Thus,

which implies. As a consequence of Proposition 2, we have which implies , which in turn implies. Since and cannot be more than 1, we get. Multiplying both sides with and arranging we get

Thus, we get. Now, combining e and f we get

Note that is positive due to the assumptions and. To see this, note implies, which implies, which implies, which implies. Thus,. Combining, , and, we conclude that the total welfare that the monopoly generates is higher than the total welfare in the duopoly industry with open source rival in the market. □

Proposition 3 shows that the competition does not necessarily increase the welfare in an oligopoly industry when compared to the monopoly market. This is because the presence of a rival induces the proprietary firm to set lower prices and those users who do not buy the proprietary firm’s product are not left empty handed; they can get the open source freely, which increases the total surplus. However, the decrease in proprietary firm’s and its users’ surpluses do not, always, need to be compensated by the increase in user-developers’ surpluses.

6. Conclusion and Discussion

In this study, a simple two-period model of open source innovation has been presented to understand the difference of the behavior of the proprietary firm’s production, pricing and investment strategies and to facilitate welfare comparisons between the presence of it and the traditional, profit driven method of development, where the quality levels of the two follow a ladder type technology framework. It has been shown that the proprietary firm decreases its production level when there is an open source rival, and in order to better compete with the open source firm, it invests more. However, the total welfare, under certain conditions, is higher in monopoly benchmark than in the duopolistic competition, where there is an open source rival.

Now, we discuss a number of directions this work could be pushed or alternative models one can consider.

Periods: When we tried to set up a model, where the number of periods is three or more, or infinitely many, we end up with technical problems of solving the first order condition of proprietary firm’s maximization problem. This problem occurs because there is no analytical solution for the number of proprietary users at period t, , when the number of potential users, N, exceeds three. Employing the known methods to solve the Bellman Equation, which captures the recursive nature of the dynamic game problem is not helpful since transition matrix that should govern the evolution of the state variables are determined by the choice variables in each period, that is, the transition matrix is not stationary.

Endogenous Bonus with OLG: We also considered an alternative model where users live for two periods. They could buy an operating system only when they are young. User-developers could develop the open source when they are young, and enjoy the appreciation of its quality when they are old, if at least one of them succeeds due to General Public License. When we model the user-developers investment incentives in this framework, with allowing the investment levels to be in interval, we faced difficulties while solving the optimal investment levels of user-developers since the optimal decisions include order equations. To overcome such difficulties, one could think of forcing the possible investment level choices of the user developers to be binary, i.e. they would be either 0 or 1. However, there occurs a free rider problem that Johnson (2002) [3] finds, too. Since it is guaranteed for the open source to be improved when one user-developer chooses to invest in 1, it is optimal for every user-developer to let someone else do it.

Contribution Game with Infinitely Many Users: When Lerner and Tirole (2002) explain the favorable characteristics for an open source production, they mention about its modularity, whether the overall project is divided into smaller and well-defined tasks (modules) that individuals can handle independently from other modules. Sufficiently modular nature of an open source software, whose different portions can be improved by independent user-developers, might turn the investment stage to a contribution game for open source user-developers. To do so, one other helpful way could be having infinitely many users distributed on. Although in our original model, that would create some compatibility problems while finding the open source firm’s development probability, since it has a multiplication part. This is not a good way to use when there are infinitely many users, that would provide a well defined demand, and is a better way to model the investment stage as a contribution game, where the probability of open source firms’ development is affected by a fraction of the measure of user-developers that contribute or all users. Such a model might also capture the direct benefit incentives of the user-developers, which would result in having different optimal investment strategies for different user-developers. To incorporate the direct benefit, a successful development of a user-developer could be rewarded by enjoying the appreciation of her own operating system before the quality increase become public.

Mixed Duopolistic Competition: In our model, the competitors have heterogeneous objective functions, thus it is a mixed duopoly model. The limitations of our model through mixed duopolistic competition may include the case where the there may be more than one proprietary and more than one open source firm. Thus, more than two proprietary firms may engage in competition with more than one open source firms, where proprietary firms may have homogeneous objective functions. However, we believe this extension would potentially be another paper.

Acknowledgements

We thank the Editor and the referee for their comments.

Cite this paper

SuatAkbulut,MuratYılmaz, (2015) A Dynamic Model of Mixed Duopolistic Competition: Open Source vs. Proprietary Innovation. Theoretical Economics Letters,05,730-738. doi: 10.4236/tel.2015.56085

References

NOTES

¹See https://www.blackducksoftware.com/resources/data/top-20-open-source-licenses/

²For example, according to its 2015 income statement, Red Hat, the world’s largest commercial distributor of the Linux operating system, made a total net income of $180.20 million in 2014.

³See also Hasnas, Lambertini and Palestini (2014) [7] , Jaisingh, See-To and Tam (2008) [8] and Suh and Yilmaz (2015) [9] .

⁴One can think of another model where there are more than two firms. However, we believe that two firm assumption does not restrict the model and its implications too much. In fact, within the open source firm, there will be many developers, which is quite realistic. Also, adding another proprietary firm will not change the results and the intuition.

⁵Holding the other operating system’s quality level constant, , where, the value of operating system i, , will increase as its quality level increases.

⁶Assumption 3 makes the objective function for Windows nicely behaved and it ensures that the difference between the technological trajectories, , does not explode.

⁷The second order condition ensures that this is the optimal solution.

⁸Note that and being linear with slope and causes to be a linear function, as well, with slope. Thus and. Assumption 2 ensures that and. Thus, is positive.