Theoretical Economics Letters
Vol.05 No.02(2015), Article ID:55241,4 pages
10.4236/tel.2015.52025
Unveiling Cost Burden Interdependencies with the Use of the Hypothetical Extraction Method
Ana-Isabel Guerra1, Ferran Sancho2
1Department of International Economics, Universidad de Granada, Granada, Spain
2Department of Economics, Universitat Autònoma de Barcelona, Bellaterra, Spain
Email: anaisabelguerra@ugr.es, Ferran.sancho@uab.cat
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 February 2015; accepted 21 March 2015; published 31 March 2015
ABSTRACT
Networked economies constitute an interlocked mechanism of direct effects and indirect feedbacks. Each piece of the mechanism plays a specific role influencing the overall performance of the system. In the setup of an interindustry economy, the interlocked pieces are typical economic sectors. Any sector influences other sectors and is in turn being influenced by them. We propose a new methodology to unveil the underlying cost linkage effects being exerted by sectors and affecting the complete price system. The methodology reformulates the Hypothetical Extraction Method, usually applied to the quantity side of the economy, and extends it to the cost side of the economy. The derived cost linkage indicators reveal valuable information that may be used in the design of tax reforms or efficiency policies. We present a practical example of the capacities of this new proposal using US data.
Keywords:
Cost Burden, Extraction Method, Interindustry Interdependencies, Price Linkages

1. Introduction
A recurring question in applied economics is the detection and measurement of the effects that an industry of an economic system exerts on the rest of that system’s industries. This question is clearly best analysed under a disaggregated general equilibrium setting since it allows for a comprehensive description of the input-output (I-O) connectedness (forward and backward) among the whole set of industries in the economy. A powerful idea is that the impact of an industry within the system can be captured under the assumption that its I-O transactions, in full or partly, cease to play a role in the economy. This is the essence of the Hypothetical Extraction Method (HEM) as introduced in [1] -[3] . The traditional application setup for the HEM has been the linear I-O quantity model as described in [4] with the main objective being the identification of dominant or key sectors on the basis of backward and/or forward quantity linkage indicators.
When, in contrast, the aim of the analysis is to evaluate the influence that an industry exerts on economy-wide cost structures, the price version of the I-O model becomes the appropriate and natural tool of choice. Quite surprisingly, however, the HEM has not been used to evaluate the cost structure of an economy, and this despite its otherwise widespread use in quantity assessments [5] . The extension of the HEM to the price model is therefore the main goal of this note. There are many alternatives available to extract a given sector (or group of sectors) from the system, see for instance [6] . We choose the option that sets to zero all the coefficients of the industry’s standing production technique. This option has the nice interpretation that the commodity produced by the extracted sector becomes a free commodity. The difference between the initial equilibrium prices and the counterfactual equilibrium prices, after the hypothetical extraction is simulated, captures the total implicit cost burden per unit of output. Thus the absence of the extracted sector explains the observed price differentials. We also pro- pose a specific way to gauge these price differentials using an absolute cost linkage indicator related to final domestic demand and a transformation that yields a relative index that makes results easier to interpret regardless of the nominal dollar values.
In Section 2, we describe the methodology used to construct the price linkage measures following our particular extension of the HEM to the price side of the economy. In Section 3, we empirically illustrate the potential of the analysis using 2011 interindustry data for the USA and Section 4 concludes.
2. Constructing Price Linkage Measures from the Hypothetical Extraction Method
We depart from an N sector interindustry economy. Each sector fulfils an inherent budget constraint for which the total value of all outlays for primary and non-primary inputs in the j industry must be equal to the value of the total gross output generated by this industry:
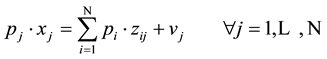 (1)
(1)
where, following standard notation,  refers to the prices per unit of gross output produced in sector j,
refers to the prices per unit of gross output produced in sector j, 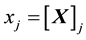 represents its gross output,
represents its gross output,  stands for total intermediate demand (domestic and imported) of commodity i by sector j while
stands for total intermediate demand (domestic and imported) of commodity i by sector j while  captures total value-added cost per sector.
captures total value-added cost per sector.
We now rescale the transaction values in Equation (1) in such a way that every one of the new units has a worth, exactly, of 1 dollar. This normalization yields the linear Leontief I-O model, where equilibrium prices are defined as:
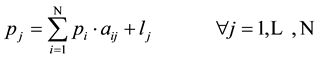 (2a)
(2a)
Alternatively, in matrix notation we have:
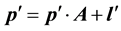 (2b)
(2b)
with 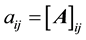 being the matrix of direct technical coefficients and
being the matrix of direct technical coefficients and  the vector of primary inputs’ requirements in value terms per unit of gross output. If matrix A is productive in economic terms, the system of Equations (2a) and (2b) can be non-negatively solved in the following way:
the vector of primary inputs’ requirements in value terms per unit of gross output. If matrix A is productive in economic terms, the system of Equations (2a) and (2b) can be non-negatively solved in the following way:
 (3)
(3)
Before we define the price linkage measure, we first provide the interpretation of the hypothetical extraction of a sector applied to the equilibrium price system in Equations (2a) and (2b). In doing so, we propose the following parallelism. The degree of influence that a sector j has in determining economy-wide price levels can be captured evaluating a hypothetical scenario whereby this sector experiments such a remarkable improvement in technological efficiency that all its technical coefficients go down to zero. Consequently, all commodities produced by this sector become free commodities under the new hypothetical scenario, i.e. the total implicit cost burden of the extracted sector “disappears” from the system, controlling for both its role as supplier and con- sumer of inputs.
We consider that these extreme efficiency improvements occur in a subset H of the N production sectors, with 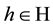 denoting the extracted sectors. Under this hypothetical scenario, the elements of the modified technological coefficient matrix
denoting the extracted sectors. Under this hypothetical scenario, the elements of the modified technological coefficient matrix 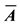 and vector
and vector 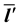 become:
become:
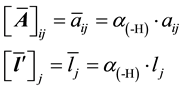 (4)
(4)
where 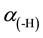 is an auxiliary binary scalar that equals 0 if j = h and is set to 1 otherwise. Therefore, the post-ex- traction equilibrium prices are computed as follows:
is an auxiliary binary scalar that equals 0 if j = h and is set to 1 otherwise. Therefore, the post-ex- traction equilibrium prices are computed as follows:
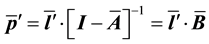 (5)
(5)
We subtract Equation (5) from Equation (3) to obtain the implicit cost burden of the extracted industries in subset H:

The price differentials in Equation (6) refer to basic units of commodities. Policy makers, however, are often interested in evaluating the incidence of a policy, such as an indirect tax reform or the implementation of efficiency stimuli, from a viewpoint that takes into account its overall impact regarding some aggregate measures such as final domestic consumption, for instance. Therefore, we can make the price linkage measure more informative if we weight the evaluated implicit cost burdens in Equation (6) by the corresponding vector of sectoral domestic final demand fd:

where the superscript ^ denotes a diagonal matrix. According to our sectoral subdivision and using partitioned matrices, we can rewrite the matrix product in Equation (7) as:

The second component of the partitioned matrix in Equation (8) can be read as the total implicit costs (direct and indirect) paid by the representative domestic consumer for the commodities of the H industries when acquiring one unit of the commodities of the N-H industries in the market. Thus, adding up for all N-H sectors in the economy using a unit vector eN-H of the appropriate dimension, we obtain the price or cost linkage indicator of the H extracted industries:

If we wish to compare price or cost linkage indicator across sectors, and thus identifying dominant sectors in these terms, we need to impose an additional criterion that would allow such comparisons. We propose to use the ratio of the implicit cost burden of the extracted subset H to the total benchmark equilibrium value of final domestic demand of the remaining N-H industries:

Consequently, the higher the value of RPL(-H), the more significant will be the total implicit cost burden of the extracted industries for the “unextracted” ones1.
3. Price Linkage Indicators for the USA Economy
We now apply the methodology outlined in the previous section to explore the hierarchy of sectors in terms of their implicit cost burden. We illustrate the empirical exercise using 2011 interindustry data for the USA economy obtained from the World Input-Output Database (WIOD); refer to [7] for a description. We keep the original 35 industry sectoral break-down provided by this database. In Table 1 we report the cost computations but only for
Table 1. Price linkage indicators. Selected sectors*. USA economy. Symmetric input-output table 2011.
the sectors whose price linkage indicator is greater than 1 percent.
The results in this Table are computed performing a sequential extraction of the complete cost structures for each and every sector of the economy; in this specific case H = i for 
According to our results, the criterion indicator RPL(-H) provides evidence that in this economy key industries in terms of cost interdependences are primarily concentrated in the services sectors, namely, in “Renting of Machinery and Equipment and Other Business Activities”, “Financial Intermediation”, “Real Estate Activities” and “Wholesale Trade and Commission Trade”. The total implicit cost burdens of these sectors represent respectively 13.181, 6.497, 3.389 and 2.899 percent of the total value of domestic final demand of the remaining sectors. In fact, these results are in line with the structural characteristics of developed economies where all these service activities play a major role as intermediaries of economic transactions, i.e. they increase the degree of connectedness in business to business flows and in business to final demand flows. Therefore, any efficiency improvements that would affect the whole cost structure of these sectors, say through investment on R + D + i activities in the service sectors, would lead to remarkable downward effects on prices.
The “Mining and Quarrying” and the “Coke, Refined Petroleum and Nuclear Fuel” industries are also important in terms of their implicit price interdependences. Therefore, an increase for instance in the taxes charged on the transactions of these energy related sectors, or in the abatement costs needed to control emissions levels generated by them, would in this case exert a significant rise in prices at an economy-wide level.
4. Concluding Remarks
We show in this report how the hypothetical extraction method can be extended to the interindustry price model to reveal the implicit cost burden exerted by each economic sector through the network of interdependencies that characterizes an economy. We propose two related indicators that, by capturing the underlying economic structure, do the job of measuring the said cost burdens. This methodological proposal could be useful in the design of policies influencing conducts that affect prices. One such example would be indirect tax policies. Another would be efficiency policies directed to promote competitiveness. In both cases, our indicators would provide a complete numerical characterization of the derived cost effects, in absolute and in ratio terms, and a corresponding ranking of sectors. Thanks to the revealed hierarchy of sectors, policy makers could use the information to adjust or tune their policies up to improve their chances of success.
References
- Paelinck, J., de Caevel, J. and Degueldre, J. (1965) Analyse Quantitative de Certaines Phénomènes du Développement Régional Polarisé: Essai de Simulation Statique d’Itinéraires de Propagation. In: Bibliothèque de l’Institut de Science Économique. No. 7. Problémes de Conversion Économique: Analyses Théoriques et Études Appliquées, M.-Th. Génin, Paris, 341-387.
- Strassert, G. (1968) Zur Bestimmung Strategischer Sektoren mit hilfe von Input-Output modellen. Jahrbucher fur Nationalokonomie und Statistick, 182, 211-215.
- Schultz, S. (1977) Approaches to Identifying Key Sectors Empirically by Means of Input-Output Analysis. Journal of Development Studies, 14, 77-96.
- Leontief, W.W. (1941) The Structure of the American Economy. Oxford University Press, New York.
- Miller, R.E. and Blair, P.D. (2009) Input-Output Analysis: Foundations and Extensions. 2nd Edition, Cambridge University Press, Cambridge.
- Miller, R.E. and Lahr, M.L. (2001) A Taxonomy of Extractions. In: Lahr, M.L. and Miller, R.E., Eds., Regional Sci- ence Perspectives in Economic Analysis: A Festschrift in Memory of Benjamin H. Stevens, Elsevier Science, Amsterdam, 407-441.
- Timmer, M., Erumban, A.A., Francois, J., Genty, A., Gouma, R., Los, B., Neuwahl, F., Pindyuk, O., Poeschl, J., Rueda- Cantuche, J.M., Stehrer, R., Streicher, G., Temurshoev, U., Villanueva, A. and de Vries, G.J. (2012) The World Input- Output Database (WIOD): Contents, Sources and Methods. http://www.wiod.org
NOTES
1In fact, it can be proved that the ratio RPL(-H) is related to the Laspeyres price index LPI measuring price changes between the initial and the extracted equilibria, through the relationship RPL(-H) = 1 − LPI(-H).



