Received 7 July 2014; revised 12 August 2014; accepted 6 September 2014

ABSTRACT

This note provides the closed-form solution for the model by Lazear [1] . The employer adjusts the performance standard for promotion when the employer observes only the imperfect index of the employee’s ability. The adjustment margin is larger when the performance depends heavily on luck and depends lightly on the employee’s ability.

Keywords:

Peter Principle, Promotion, Employer’s learning

1. Introduction

The Peter Principle claims that an employee is promoted to the rank at which the employee exhibits his incompetence. Lazear [1] attributes the observation to the statistical mean reversion. The employer promotes an employee if the employee’s performance exceeds a certain threshold. When the employee’s performance depends partly on luck, a lucky employee is more likely to be promoted. The promoted employee’s performance necessarily declines, on average, because the good luck does not persist after his promotion. Lazear [1] argues that the observed decline has nothing to do with misassignment, because the employer accounts for the mean reversion of the employee’s performance when setting the promotion threshold. Lazear [1] qualitatively characterizes the promotion threshold, and provides several numerical examples for this threshold, but does not provide the closed-form solution. This note provides the closed-form solution for the model under normality assumptions on ability and productivity-shock distributions to explicitly demonstrate the model’s rich implications.

2. Setup

An employer hires an employee whose performance in period 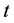depends on ability 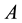and a random shock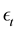. There are two periods in the production, and there are two types of jobs. Output in period is

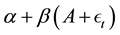in the easy job and 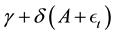in the difficult job. Given and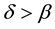, an employer

with high productivity has a comparative advantage in the difficult job. If the employer is risk neutral and can

observe the employee’s ability, the employer assigns the employee with 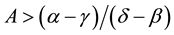to the difficult

job. The challenge for the employer is assigning the employee to either a difficult job or an easy job in period two, after observing the noisy measure of ability 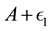that can be backed out from the first-period output in either job.

The employer knows the probability density function 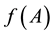and. The ability 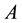has a unimodal and

symmetric distribution. The productivity shock 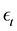is independently distributed across periods and symmetri- cally distributed with a zero mean. With knowledge of the distributions, the employer updates the subjective ability distribution of a specific employee using the error-ridden index of his ability.

The employer promotes the employee if the first-period performance 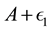exceeds a threshold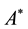. The employer’s problem is to set the threshold to maximize the expected output:

(1)

using the fact that is independent from and and has a zero mean.

The first-order condition of the output maximization problem is:

(2)

Lazear [1] does not explicitly solve the problem. Instead, he rearranges the first-order condition so that

(3)

by replacing or. Assuming to be a unimodal and symmetric distribution and that less

than one half of the employees should be promoted (is above the median of ability distribution),

. Then, which implies

(4)

Since and, follows. This is how Lazear [1] shows that the

employer inflates the promotion threshold to account for the expected decline after a promotion. He also points to the deflated promotion threshold when more than one half of the employees should be promoted (is below the median of the ability distribution).

3. The Closed-Form Solution

We obtain the closed-form solution for the model, assuming and. With

these assumptions, we can rewrite the first-order condition such that

(5)

The terms in the exponential function can be decomposed into terms that do not contain the random variable and a term containing it, as follows:

(6)

where.

Using this result, the first-order condition becomes:

(7)

By defining, the equation becomes

(8)

Using the facts that the probability-density function of the normal distribution with mean

and variance integrates to 1 and has the expected value, the first-order condition

becomes:

(9)

Dividing the first-order condition by common factors renders:

(10)

This leads to the solution:

(11)

4. Implications

Lazear [1] provides numerical solutions on page 147 under the normality assumptions on, and the

parameter values, , , , ,. For the case of, Lazear’s [1]

is close to our solution. For the case of, Lazear’s [1] is again close to

our solution. The examples make a point that the employer sets a higher threshold if the performance depends heavily on luck, because the employer expects a severe performance decline in the second period.

The closed-form solution preserves the predictions in the original model. In a typical case in which fewer than

one half of employees are eligible for promotion, , in order to compensate for the expected decline, the employer sets a higher threshold for promotion than the case when the employer perfectly observes the employee’s ability. This threshold premium is larger when the employer knows that the first-period performance depends heavily on luck and depends lightly on ability so that is larger. The argument reverses when more than one half should be promoted,. The employer thus discounts the threshold, expecting a future rise of the employee’s performance, particularly when the first-period output depends heavily on luck and depends lightly on ability.

Acknowledgments

This work was supported by JSPS KAKENHI Grant Numbers 23330079 and 11J02356. This support is greatly appreciated.

Cite this paper

ShotaAraki,DaijiKawaguchi, (2014) The Promotion Rule under Imperfect Observability of the Employee’s Ability. Theoretical Economics Letters,04,662-665. doi: 10.4236/tel.2014.48084

References