Theoretical Economics Letters
Vol.4 No.6(2014), Article
ID:46834,10
pages
DOI:10.4236/tel.2014.46053
A Probabilistic Theory for Intertemporal Indifference
Mehraj Bin Yasaar Parouty*, Maarten Jacobus Postma
University of Groningen, Groningen, The Netherlands
Email: *mehrajp@live.co.uk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 March 2014; revised 10 April 2014; accepted 1 May 2014
Abstract
This paper provides a closed form distribution for the probability of intertemporal indifference between a certain quantity of a commodity now, 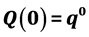 , and some future quantity
, and some future quantity 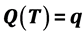 at time t = T assuming a discount weight,
at time t = T assuming a discount weight,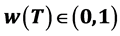 .
.
Keywords
Intertemporal Indifference, Commodity

1. Introduction
This paper combines two psychological posits, through Leibniz’s Principle of sufficient reason, to provide a probabilistic theory for intertemporal indifference. Leibniz’s principle, often associated with ex nihilo nihil fit1, has been influential in the thinking of several philosophers and was recognised as one of the four laws of thought in the 18th century. The principle states that the occurrence/existence/truthfulness of an event/entity/ statement implies the occurrence/existence/truthfulness of a sufficient explanation. In this paper, we will repeatedly make use of this principle, especially in condensing two psychological theories: the theory that we generally prefer to consume now than to consume in the future and the theory that our perception of time does not need to coincide with the “hourglass” passage of time. Through Leibniz’s principle, we aim to achieve face validation of a probabilistic theory for intertemporal indifference.
Patterns of intertemporal indifferences have captured the interest of psychologists and economists for several decades. Procrastination, addiction and willingness to save are a few observed behaviours involving time tradeoffs [1] . It is generally observed that animals or human beings weigh the future with a discount weight, 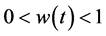 , compared to the present where the weight attached to a consumption now is exactly 1. A series of studies suggest that cognitive considerations might explain such empirical observations. For example, the primate, Saguinus oedipus, commonly referred to as the cotton-top tamarin, and common marmosets, Callithrix jacchus, are known to differ in their respective levels of temporal discounting [2] . Among the human species, age, health states, education level, to name a few, are endogeneous determinants of time preferences [3] .
, compared to the present where the weight attached to a consumption now is exactly 1. A series of studies suggest that cognitive considerations might explain such empirical observations. For example, the primate, Saguinus oedipus, commonly referred to as the cotton-top tamarin, and common marmosets, Callithrix jacchus, are known to differ in their respective levels of temporal discounting [2] . Among the human species, age, health states, education level, to name a few, are endogeneous determinants of time preferences [3] .
A very general discount weight function is of the form,  where
where 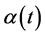 is the time-perception function and
is the time-perception function and 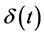 is the time-preference rate function. Several authors have sought the proper functional form by eliciting either
is the time-preference rate function. Several authors have sought the proper functional form by eliciting either 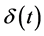 or
or 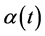 or both. Albrecht and Weber [4] , for example, propose that individuals have a non-linear time preception function. The weight,
or both. Albrecht and Weber [4] , for example, propose that individuals have a non-linear time preception function. The weight, 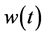 , they proposed is given by
, they proposed is given by 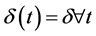 and
and  is the non-linear time perception function indicating how fast time is perceived to pass in an individual’s mind. Other authors assumed a linearly declining discount rate function,
is the non-linear time perception function indicating how fast time is perceived to pass in an individual’s mind. Other authors assumed a linearly declining discount rate function, 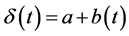 [5] or a discontinuous hyperbolic discount weight function [6] [7] or an implicit function for the weight such as Loewenstein and Prelec’s
[5] or a discontinuous hyperbolic discount weight function [6] [7] or an implicit function for the weight such as Loewenstein and Prelec’s 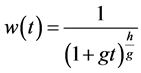 [8] .
[8] .
Empirical investigations on time preferences have, however, rarely converged [9] . Consequently, rather than claiming a certain functional form for time preference, in this paper, our main assumption shall be that
• An individual is expected to value a future quantity compared to a current quantity, q0, by placing a discount weight, 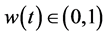 , on the future quantity, i.e.
, on the future quantity, i.e. 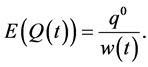
With an expectation in place, we, next, seek to identify the source of variability. Among the different senses of the human being, time perception is a sense that is increasingly gaining the interest of psychologists. A key issue in modern neuroscience is the association that an individual’s perception bears with her neural events [10] . Several studies have found that the speed of the internal clock is linked to the concentration of dopamine in the basal ganglia (see for example Meck [11] ). The sense of time is often argued to be a consequence of the dopaminergic state, influencing the sensory signal-to-noise ratio due to an effect of dopamine at the cellular level [12] [13] . As Einstein described relativity with the faster passage of time when one sits in the company of a beautiful woman, it would also not be implausible that, everything else being constant, cognitive processes allow the “present time” to be viewed as a random variable.
Strictly speaking, the present is an infinitely small-time interval separating the past and the future. However, it is argued that the perceived present, or the so-called specious present, is an interval which needs not be infinitely small—a concept first observed in 1882 [14] . Furthermore, since the passage of time allows any future time interval to be constructed by a sequence of the individual’s specious presents, then we have a time-inhomogeneous stochastic process similar to Parouty [15] . So, similar to Samuelson [16] who condensed the disparate psychological motives towards time preference into the discount rate [9] , the source of variability that we identified effectively condenses the disparate psychological factors adding variability across an individual’s intertemporal indifference into a mathematically tractable parameter; i.e. into the variability of the specious present. Then, we can analyse the sentence: “In general, individuals prefer to consume now than to consume in the future” with focus on the word “in general” and reformulate the latter sentence into a more statistically interpretable form.
The assumption that an individual’s perception of a future interval is a sequence of random specious presents coupled with the assumption that the individual is expected to place a weight on future consumption are sufficient assumptions to formulate a probabilistic distribution for intertemporal indifference—a direct consequence of Leibniz’s principle. Given that perceived passage of time is not always equal to hour-glass passage of time and that individuals generally prefer to consume now than in the future, then from Leibniz’s Principle of sufficient reason, the existence of an intertemporal indifference probability distribution is implied.
2. Distribution
The assignment of probability measures is done by deriving a maximum entropy distribution for the probability that an individual/animal is indifferent between some quantity 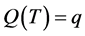 at time
at time 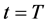 and a given quantity
and a given quantity 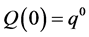 now. First, we write our expectation in a more structured language, so that, given an initial amount,
now. First, we write our expectation in a more structured language, so that, given an initial amount, 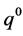 , now, the expected indifference amount at time t is
, now, the expected indifference amount at time t is
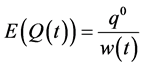 (1)
(1)
With Equation (1) being the unconditional expectation of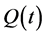 , the Radon-Nykodym theorem asserts the existence of a conditional infinitesimal expectation [17] . Defining
, the Radon-Nykodym theorem asserts the existence of a conditional infinitesimal expectation [17] . Defining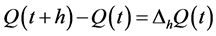 , the conditional infinitesimal expectation is given by
, the conditional infinitesimal expectation is given by
 (2)
(2)
Next, it is important to note that an individual or animal will only express a time preference provided she perceives time to pass (or provided the interval of time that she perceives is bigger than her specious present). Since the specious presents are random time durations, we can assume that a given fixed indifference amount at a specific time point has a random duration being equal to the individual’s specious present at that time. Furthermore, at the instant that the next specious present begins, the indifference amount increases continuously with certainty. Thus, we ensure that an individual’s intertemporal indifference path is a continuous function of time. As a result the process adheres to the typical characterisations of diffusion processes; usually restricted by a jump constraint on their probability measure,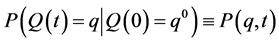 . To be more specific, for a positive
. To be more specific, for a positive 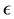 sufficiently small,
sufficiently small,
 (3)
(3)
Equation (3) ensures that the indifference path is time-continuous. For example, an individual being given an amount q0 now will always be indifferent to the same amount, q0, in any future interval which lies in her specious present. It is at the instant the new specious present begins that the individual’s indifference path exits the state q0 moving, at all times, along a cádlág path2.
2.1. Probability Assignment
We now wish to assign probability measures such that the surprisal or hidden information is maximized. Surprisal maximization is the standard principle in devising probability distributions. According to the principle of maximum-entropy, if we have a partial knowledge about a random variable (whether it is discrete or continuous, it’s range, mean, etcetera), we first obtain a family of probability distributions that are all consistent with our information and then, we select, from that family, the single distribution whose uncertainty is the greatest. Most commonly used distributions are MaxEnt3 given a current state of knowledge. For example, if we know nothing about a system of continuous random variables except it’s range, we get the uniform distribution, or except it’s positive mean, we get the exponential distribution, or except it’s mean and standard deviation, we get the normal distribution, and so on.
Consequently, with the given infinitesimal mean, Equation (8.2), we first devise a MaxEnt distribution for a sufficiently small time interval, h, and thereafter we shall project that distribution through time given the constraint that, for sufficiently small h, 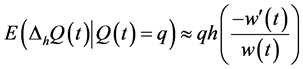 , to obtain a probability distribution.
, to obtain a probability distribution.
Note that the infinitesimal distribution, at any time, would be very much dependent on the weight function, 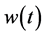 , at that specific time. In the small enough time interval, h, in case of continuous intertemporal preferences, I consider the Dirac measure,
, at that specific time. In the small enough time interval, h, in case of continuous intertemporal preferences, I consider the Dirac measure,  which identifies4 an exit from a preference amount q in the interval
which identifies4 an exit from a preference amount q in the interval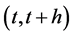 . The Lagrangian is given by
. The Lagrangian is given by
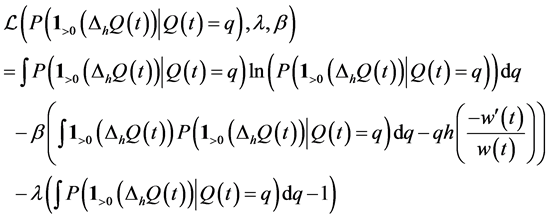
Differentiating 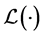 with respect to
with respect to 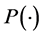 yields
yields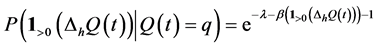 . Picking
. Picking  and
and 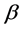 so that
so that  is a probability measure and
is a probability measure and 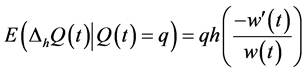 gives
gives
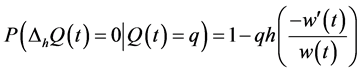 (4)
(4)
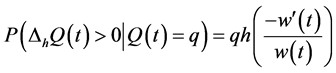 (5)
(5)
It is interesting to remark that the use of the Dirac measure above assumes unit jumps and hence Equations (4) and (5) provide a good analogy for countable indifference amounts, such as euros5. Furthermore, let us assume that we observe the individual for an instant, or, say, for a sufficiently small time interval6. At that instant, either the individual would have perceived time to pass or not and, consequently, either there exists an exit from a preference amount or not; wherefore we obtained Equations (4) and (5) which formed the infinitesimal distribution. Equation (1) however requires that 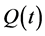 be continuous and thus hints towards the use of differentials in probability with respect to q. We do so, however, after formulating the Chapman-Kolmogorov equations.
be continuous and thus hints towards the use of differentials in probability with respect to q. We do so, however, after formulating the Chapman-Kolmogorov equations.
2.2. Differential Equation
The general Chapman-Kolmogorov equation is given by
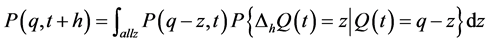 (6)
(6)
In our case, since we have only two possible outcomes in the interval h, no growth or an infinitesimal growth as specified in Equation (2), our Chapman-Kolmogorov is then approximately:
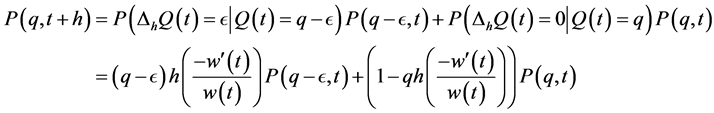
giving
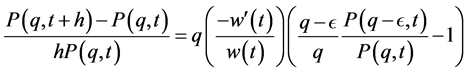
Consider the backward difference operator, . Letting
. Letting 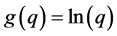 and
and 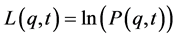 , the Chapman-Kolmogorov equation becomes,
, the Chapman-Kolmogorov equation becomes,

Now, since 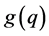 and
and 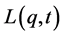 are both assumed to be analytic and successively differentiable upto some order, using Cauchy’s mean value theorem, we can write
are both assumed to be analytic and successively differentiable upto some order, using Cauchy’s mean value theorem, we can write
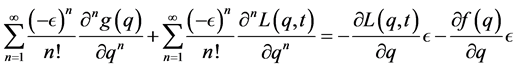
where 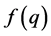 is some analytic function7. The Chapman-Kolmogorov equation can thus be written as
is some analytic function7. The Chapman-Kolmogorov equation can thus be written as
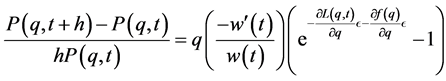 (7)
(7)
Now, taking 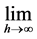 of Equation (7) and recalling that we used the Dirac measure gives:
of Equation (7) and recalling that we used the Dirac measure gives:
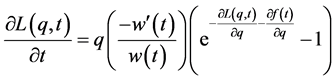 (8)
(8)
2.3. Distribution
Equation (8) can be readily solved through standard methods [18] . We note that the equations of the tangent planes to the surface satisfying Equation (8) at arbitrary points  form an envelope which is the actual surface
form an envelope which is the actual surface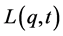 . Then taking
. Then taking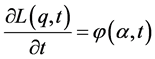 ,
, 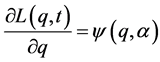 and treating
and treating  as a constant, we no longer have a partial differential equation. We can thus let
as a constant, we no longer have a partial differential equation. We can thus let 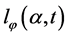 and
and 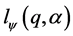 be the solutions to each, respectively, and obtain the complete integral which is a two parameter family of planes:
be the solutions to each, respectively, and obtain the complete integral which is a two parameter family of planes:
 (9)
(9)
where c is a constant independent of q and t. Writing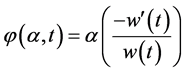 , we get
, we get
 (10)
(10)
Next, with 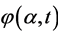 given as above, we have
given as above, we have 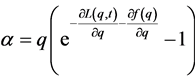 which implies
which implies  with solution
with solution
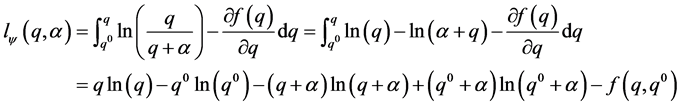 (11)
(11)
Substituting Equations (11) and (10) into Equation (9) gives
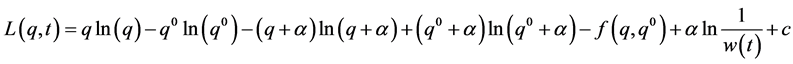 (12)
(12)
Next, we need to eliminate  from Equation (12) which we do by giving
from Equation (12) which we do by giving 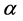 a pair of equal values for the same values of
a pair of equal values for the same values of 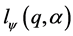 and
and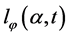 . We thus form the equation
. We thus form the equation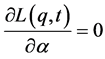 , giving
, giving
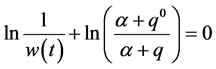 (13)
(13)
from which, we get
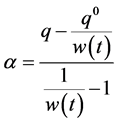 (14)
(14)
Again, substitution of  from Equation (14) into Equation (12), gives, after some algebraic simplifications,
from Equation (14) into Equation (12), gives, after some algebraic simplifications,
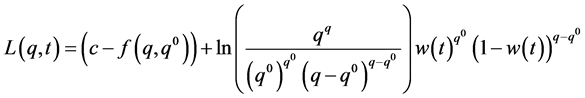 (15)
(15)
resulting in
 (16)
(16)
Integrability on the probability space, 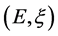 , requires picking c and
, requires picking c and  so that
so that 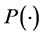 is a probability measure. Letting
is a probability measure. Letting 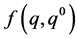 be the truncated parts of Binet’s formula for reals [19] ,
be the truncated parts of Binet’s formula for reals [19] ,
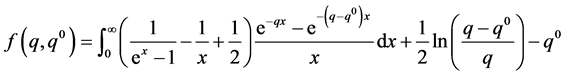
and putting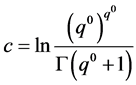 , we have a Gamma-Poisson mixture type distribution
, we have a Gamma-Poisson mixture type distribution
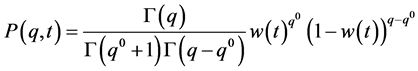 (17)
(17)
2.4. Remarks
It’s not unimportant to note that the probability distribution is not a distribution for time preferences but rather a distribution for intertemporal indifferences. To be more precise, we find a closed-form distribution for the probability that an individual will actually be indifferent between some quantity of 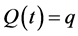 at time t and a given quantity
at time t and a given quantity 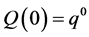 now and the individual does not imagine, today, a future quantity that she feels she will be indifferent to, compared to a given current quantity
now and the individual does not imagine, today, a future quantity that she feels she will be indifferent to, compared to a given current quantity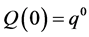 . The distribution thus cannot be applied in typical empirical time preference investigations devised thus far; although knowledge of the exact variability in the neuro-networks involved in the construction of time in an individual’s mind could allow for a proper mathematical writing.
. The distribution thus cannot be applied in typical empirical time preference investigations devised thus far; although knowledge of the exact variability in the neuro-networks involved in the construction of time in an individual’s mind could allow for a proper mathematical writing.
3. Discussion
An important assumption that we made is that we have assumed that the animal/individual lives forever implying that a choice can always be made. In case of investigations involving mortality, the latter can be rectified by taking into account mortality tables or parametric mortality laws and conditioning the probability of a choice on the probability that the choice exists. That specification is beyond this paper since it is more useful for us to assume that the individual lives forever as the latter assumption appears fairly well-founded for society. It is thus necessary that we discuss the assumptions under which the distribution is valid for society.
We will first assume that society lives forever8 and second, we will assume that society possesses a societal sense of time as with the “average” individuals comprising it. Individuals with Parkinson’s disease, attention deficit hyperactivity disorder (ADHD) and schizophrenia have a marked difference in time perception compared to an “average” individual [20] -[22] .
Consequently, even the “average” individual is bound to experience a marked alteration in time perception if drugs, such as psilocybin [23] , increasing the function of dopamine9, become common usage. Although the latter appears farfetched, an economic scenario entailing a general alteration in the “average” individual’s time perception appears reasonably realistic. Neurobiologists and psychologists often make the following associations: opioid = pleasure, dopamine = happiness, serotonin deficit = depression, oxytocin = love, nucleus accumbens = reward or amygdala = fear, etcetera [24] . Economists, on the other hand, would coin a bullish or a bearish sentiment, reflecting a positive or a negative feeling about market trends. A society with a bull market, a market with an upward trend, for example, might experience time to pass faster than one with a market with a downward trend—a bear market, say10.
As such, we assume some ethical11 weights among the preferences of individuals comprising a temporal society so that we can assume that society, as a whole, also experiences the passage of time as a sequence of societal specious presents. Then a society will be indifferent to a single fixed quantity for the duration of its specious present, before feeling the need for some extra amounts, with a social rate of time preference, srtp, when it perceives the present to have become past. Moreover, we can also assume non-subjective rates.
Although, our considerations, thus far, have only concerned a subjective rate of time preference, in the case where rates are not subjective, such as the rate on government bonds, without loss of generality, the probability of intertemporal indifference for a society with an external social discount rate, SDR, can be equivalently seen to follow the same distributional laws as given in Equation (8) since the main source of variability is assumed to be in the perception of time. To be specific, the expectation is taken as given and it is only the occurrence times of events, identified by zeroes or ones, which are random and assigned probability measures through surprisal maximization. So, society’s probability of intertemporal indifference, 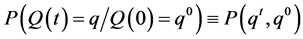 can be represented by Equation (17).
can be represented by Equation (17).
References
- Dasgupta, P. and Maskin, E. (2005) Uncertainty and Hyperbolic Discounting. American Economic Review, 95, 1290-1299. http://dx.doi.org/10.1257/0002828054825637
- Rosati, A.G., Stevens, J.R. and Hauser, M.D. (2006) The Effect of Handling Time on Temporal Discounting in Two New World Primates. Animal Behaviour, 71, 1379-1387.
http://dx.doi.org/10.1016/j.anbehav.2005.11.012 - Parouty, M.B.Y., Le, H.H., Krooshof, D. and Postma, M.J. (2014) Differential Time Preferences for Money and Quality of Life. Pharmacoeconomics, 32, 411-419. http://dx.doi.org/10.1007/s40273-013-0124-8
- Albrecht, A. and Weber, M. (1995) Hyperbolic Discounting Models in Prescriptive Theory of Intertemporal Choice. Zeitschrift fur Wirtschaftsund Sozialwissenschaften, 115, 535-568.
- Cropper, M.L., Aydede, S.K. and Portney, P.R. (1992) Rates of Time Preference for Saving Lives. The American Economic Review, 82, 460-472.
- Bazelon, B. (2002) Discounting in the Long Term. Loyala of Los Angeles Law Review, 35, 277.
- Beutels, P., Scuffham, P.A. and MacIntyre, C.R. (2008) Funding of Drugs: Do Vaccines Warrant a Different Approach? The Lancet Infectious Diseases, 8, 727-733. http://dx.doi.org/10.1016/S1473-3099(08)70258-5
- Loewenstein, G.F. and Prelec, D. (1992) Anomalies in Intertemporal Choice: Evidence and an Interpretation. Quarterly Journal of Economics, 107, 573-597. http://dx.doi.org/10.2307/2118482
- Frederick, S., Loewenstein, G. and O’Donoghue, T. (2002) Time Discounting and Time Preference: A Critical Review. Journal of Economic Literature, XL, 351-401. http://dx.doi.org/10.1257/jel.40.2.351
- Crick, F. and Koch, C. (2003) A Framework for Consciousness. Nature Neuroscience, 6, 119-126. http://dx.doi.org/10.1038/nn0203-119
- Meck, W.H. (1996) Neuropharmacology of Timing and Time Perception. Cognitive Brain Research, 3, 227-242. http://dx.doi.org/10.1016/0926-6410(96)00009-2
- Williams, G.V. and Goldman-Rakic, P.S. (1995) Modulation of Memory Fields by Dopamine D1 Receptors in Prefrontal Cortex. Nature, 376, 572-575. http://dx.doi.org/10.1038/376572a0
- Winterer, G., Ziller, M., Dorn, H., Frick, K., Mulert, C., Wuebben, Y., et al (2000) Schizophrenia: Reduced Signal-To-Noise Ratio and Impaired Phase-Locking during Information Processing. Clinical Neurophysiology, 111, 837-849. http://dx.doi.org/10.1016/S1388-2457(99)00322-3
- Holly, A. and Grush, R. (2009) A Brief History of Time-Consciousness: Historical Precursors to James and Husserl. Journal of the History of Philosophy, 47, 277-307. http://dx.doi.org/10.1353/hph.0.0118
- Parouty, M.B.Y. (2013) Inequality Aversion to Posterity: Discounting Human Lives.
- Samuelson, P. (1937) A Note on Measurement of Utility. Review of Economic Studies, 4, 155-161. http://dx.doi.org/10.2307/2967612
- Varadhan, S.R.S. (2001) Probability Theory. American Mathematical Society, Providence, 79-80.
- Forsyth, A.R. (1929) A Treatise on Differential Equations. 6th Edition, Macmilian, London, 412-414.
- Zoltan, S. (1999) An Elementary Proof of Binet’s Formula for the Gamma Function. The American Mathematical Monthly, 106, 156-158. http://dx.doi.org/10.2307/2589052
- Levy, F. and Swanson, J.M. (2001) Timing, Space and ADHD: The Dopamine Theory Revisited. Australian and New Zealand Journal of Psychiatry, 35, 504-511. http://dx.doi.org/10.1046/j.1440-1614.2001.00923.x
- Pastor, M.A., Artieda, J., Jahanshahi, M. and Obeso, J.A. (1992) Time Estimation and Reproduction Is Abnormal in Parkinson’s Disease. Brain: A Journal of Neurology, 115, 211-225.
- Davalos, D.B., Kisley, M.A. and Ross, G.R. (2002) Deficits in Auditory and Visual Temporal Perception in Schizophrenia. Cognitive Neuropsychiatry, 7, 273-282.
http://dx.doi.org/10.1080/13546800143000230 - Wittmann, M., Carter, O., Hasler, F., Cahn, B.R., Grimberg, U., Spring, P., Hell, D., Flohr, H. and Vollenweider, F.X. (2007) Effects of Psilocybin on Time Perception and Temporal Control of Behavior in Humans. Journal of Psycho-pharmachology, 21, 50-64.
http://dx.doi.org/10.1177/0269881106065859 - Kringelbach, M.L. and Berridge, K.C. (2003) Towards a Functional Neuroanatomy of Pleasure and Happiness. Trends in Cognitive Sciences, 13, 479-487. http://dx.doi.org/10.1016/j.tics.2009.08.006
Appendix: Probability of the Future Monetary Value of Health
The distribution derived in the previous section is noted to construct on the Dirac measure, 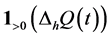 , which identifies an exit from a preference amount q in the interval
, which identifies an exit from a preference amount q in the interval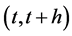 . Consequently, the infinitesimal distribution, given by Equations (8.4) and (8.5), also satisfy discrete increments12. That is
. Consequently, the infinitesimal distribution, given by Equations (8.4) and (8.5), also satisfy discrete increments12. That is
 (18)
(18)
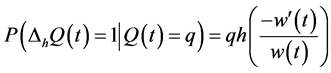 (19)
(19)
are probability measures that maximise the entropy in the time interval, 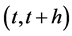 given the constraints aforementioned. Thus, although
given the constraints aforementioned. Thus, although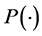 , given by Equation (17), is a continuous state process, we considered increments of one and allowed a continuous function to pass through those increments by the use of differentials. As a result, the discrete version of Equation (17), is obtained by converting the
, given by Equation (17), is a continuous state process, we considered increments of one and allowed a continuous function to pass through those increments by the use of differentials. As a result, the discrete version of Equation (17), is obtained by converting the  functions to their factorial equivalents, obtaining a Yule-Furry type process:
functions to their factorial equivalents, obtaining a Yule-Furry type process:
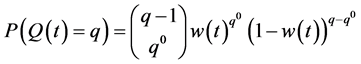 (20)
(20)
Thus, for an individual considering outcomes that are discrete such as the Euro or the QALY, Equation (20) gives the probability that the individual is indifferent between some quantity 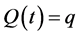 at time
at time 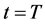 and a given quantity
and a given quantity 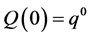 now given a discount weight,
now given a discount weight,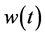 .
.
With a distribution for the probability of intertemporal indifference, it is feasible to make probabilistic statements about the monetary value of health in the future. We recall that differential discounting is pedantically establishable provided the monetary value of health is non-constant with respect to time. Let the probability that an individual is indifferent between some quantity of money 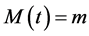 at a future time t and a given quantity of money
at a future time t and a given quantity of money 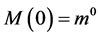 now be
now be
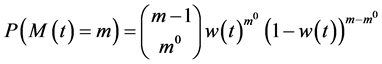
and let the probability that the individual is indifferent between some measurable quantity of health 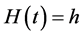 at a future time t and a given quantity of health
at a future time t and a given quantity of health 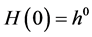 now be
now be
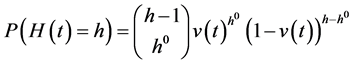
where the function 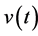 is possibly different from
is possibly different from . Given the current monetary value of health,
. Given the current monetary value of health,  we wish to find the probability that at a future time, t, the monetary value of health will be the same. With
we wish to find the probability that at a future time, t, the monetary value of health will be the same. With 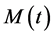 and
and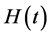 , being random variables, the monetary value of health is also a random variable. Let us consider the change of variables
, being random variables, the monetary value of health is also a random variable. Let us consider the change of variables
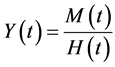 (21)
(21)
and
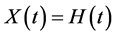 (22)
(22)
We wish to find the distribution of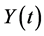 . Since
. Since  and
and 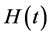 are two independent random variables, their joint p.d.f is given by
are two independent random variables, their joint p.d.f is given by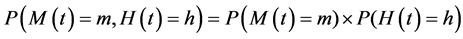 . Now, with
. Now, with 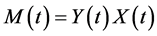 and
and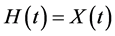 , and the Jacobian
, and the Jacobian
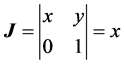
the joint distribution of 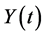 and
and 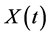 is given by
is given by
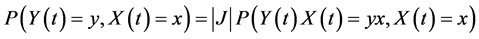
which equals
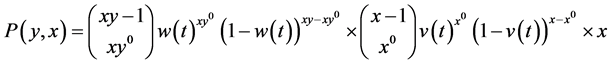
The distribution of  can thus be obtained by marginalizing out
can thus be obtained by marginalizing out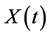 ; i.e.
; i.e. 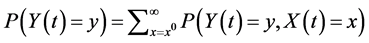 . The computation, however, requiring complex mathematics13, might be numerically approximated using today’s advanced softwares. Alternatively, rather than naively finding the solution, one might attempt to bound the probability, depending on one’s objectives.
. The computation, however, requiring complex mathematics13, might be numerically approximated using today’s advanced softwares. Alternatively, rather than naively finding the solution, one might attempt to bound the probability, depending on one’s objectives.
NOTES

*Corresponding author.
1A Latin expression, argued in the first thesis of Parmenides, 5th century BCE, meaning nothing comes from nothing.

2Cádlág means right continuous with left limits.
3MaxEnt is short for maximum-entropy.
4 takes a value of 1 if
takes a value of 1 if 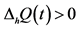 and takes a value of 0 if
and takes a value of 0 if 

5That is, for example, given an individual’s indifference amount, 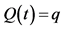 at time t, the probability that in the small time interval,
at time t, the probability that in the small time interval, 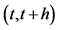 , the individual will not demand any more money is
, the individual will not demand any more money is  and the probability that the individual will demand 1 in the interval, h, is
and the probability that the individual will demand 1 in the interval, h, is 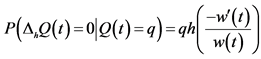 which is a valid Bernoulli distribution.
which is a valid Bernoulli distribution.
6One could take the standard unit of time, the second, defined to be the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom, as an approximation.

7Note that the assumption of a general analytic function provides more room towards later formulating a normalizing constant.

8We will assume that, through our children, we renew the link that binds the chain of our humanity through time and attain “some kind of infinity”. A specific type of infinity, as an example, here, is an actual infinity if we can assume that time is an entity.
9While dopamine is known to play a role in both our reward system and our time perception, nor epinephrine and serotonin are also argued affect the sense of time.
10Bull and bear are the symbolic beasts of finance.
11The term ethical is used here because of the numerous discussions regarding whose preferences should count. For example, educated individuals generally have different rates of time preference compared to uneducated ones . Such discussions are, however, beyond the scope of this paper.

12See appendix of this chapter for a discrete state continuous time process.

13The main problem is the quasi-absolute lack of literature on .
.

