ABSTRACT

The decision about how much to save for retirement is likely to be dependent on when an individual plans to be retired, and vice versa. Yet, the established literature on hyperbolic discounting and life-cycle saving behavior has for the most part abstracted from choice over retirement. Two notable exceptions are Diamond and Kőszegi [1] and an important follow-up study by Holmes [2], which demonstrates that time-inconsistent retirement timing is impossible when saving behavior is explicitly modeled in a stylized three-period setting. In this paper, we build upon the framework of Diamond and Kőszegi [1] and Holmes [2] by generalizing the assumptions about initial income and assets. We show analytically and via simple numerical examples that time-inconsistent retirement can exist in a three-period life-cycle model of consumption and saving.

1. Introduction

Research findings from psychology have been used to gain insight into many of the important questions that are typically studied by economists. A prominent example is that of hyperbolic discounting, in which a sizable body of research has documented that hyperbolic discount functions provide a better fit to choice data relative to the exponential discount function.^1,2 A hyperbolic discount function is characterized by a discount rate that declines in the delay. And as demonstrated in the influential study of Strotz [11], a non-constant discount rate in the delay engenders time-inconsistent preferences. Accordingly, hyperbolic discounting has become a conventional way to model and study life-cycle decision making when an individual is impulsive and has problems in following through with formulated plans or intentions.

Excessive debt and delayed saving for retirement are some of the most important economic applications of hyperbolic discounting.³ Yet, the established literature on hyperbolic discounting and life-cycle saving behavior has generally abstracted from choice over labor supply. Although understandable given the additional complexity that might exist as a result of having multiple margins of time inconsistency, it is conceivable that ignoring labor supply decisions could lead to skewed predictions about the effect of hyperbolic discounting on saving outcomes. This is due to the possibility that saving and labor supply decisions are determined in tandem. Indeed, the decision about how much to save for retirement is likely to be dependent on when an individual plans to be retired (the extensive labor supply decision), and vice versa.

The study by Diamond and Kőszegi [1] was the first theoretical investigation into the effects of hyperbolic discounting on the retirement decision. In an important follow-up study, Holmes [2] shows that time-inconsistent retirement timing is impossible when saving behavior is explicitly modeled within a simple three-period setting of the variety used by Diamond and Kőszegi [1]. Yet, Holmes [2] hypothesizes that “a more general T-period model” (p. 130) might lead to time inconsistency in the retirement decision. Indeed, this is verified in Findley and Caliendo [13] using a continuous-time model that examines the effects of hyperbolic discounting on saving behavior when retirement is endogenous. In this paper, we point out that time-inconsistent retirement can also exist in a three-period setting with a slight generalization of the assumptions about initial income and assets.⁴ This is important given the prevalence of studies in the fields of public economics and macroeconomics that use threeperiod life-cycle/overlapping-generations models to assess the effects of government policies regarding retirement.

2. Theoretical Framework

An individual lives for three periods and acquires utility from consumption and from leisure. The utility acquired from consumption each period is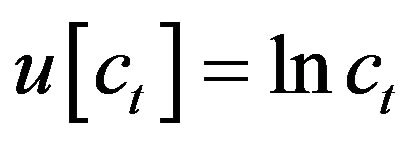, where is consumption in period. Leisure in period 1 and period 3 is exogenously imposed, namely 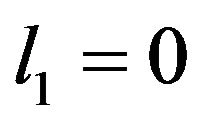and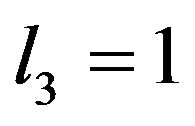. The representative individual has choice over leisure in period 2 such that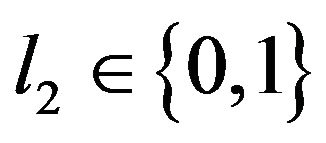, where 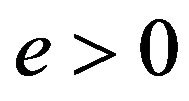is the period utility of leisure (the cost of working). From the perspective of the first period, the intertemporal utility function of the individual is

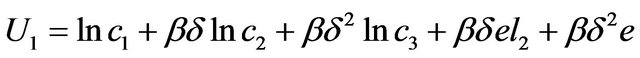(1)

where 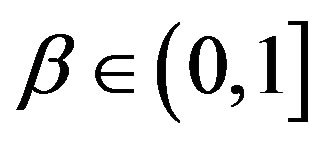and 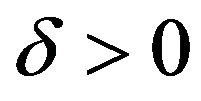are the short-term and longterm discount factors. From the perspective of the second period, the intertemporal utility function is

(2)

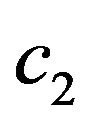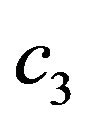Note that if, then (1) is not consistent with (2), meaning that the marginal rate of substitution between and is 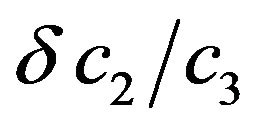from the perspective of period 1, yet it is from the perspective of period 2. We assume that the individual is naive about his time-inconsistent preferences. This means that in period 1 the individual selects an allocation of consumption and leisure that he believes will be followed in the current and in future periods in order to maximize (1). Yet, the individual will update his choices in period 2 such that (2) is maximized.

We generalize the setup of Diamond and Kőszegi [1] and Holmes [2] such that the representative individual makes choices in period 1 with cash on hand, , which can consist of current labor income and financial wealth.⁵ The individual earns unit income in period 2 if he chooses to actually work. Therefore, the individual’s constraints in periods 1 and 2 are respectively

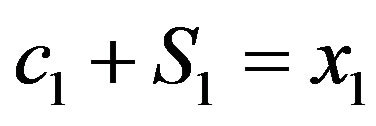(3)

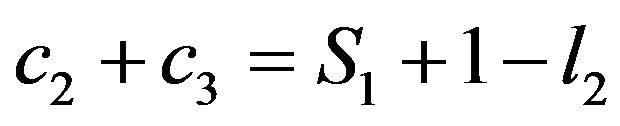(4)

We assume a zero interest rate, but we do not impose any restrictions on S₁. Yet, 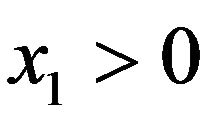and 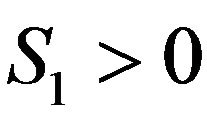are necessary to entertain the possibility of retirement in period 2.

2.1. Optimization in Period 1

With the superscript on the choice variables denoting the period of planning, the individual plans to consume

(5)

with 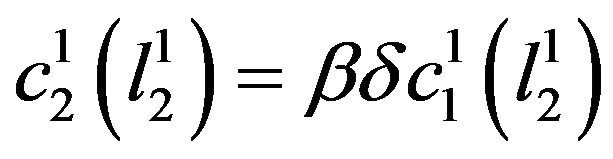and, given the individual’s period-1 intention of his period-2 leisure choice,. These intentions imply period-1 savings,

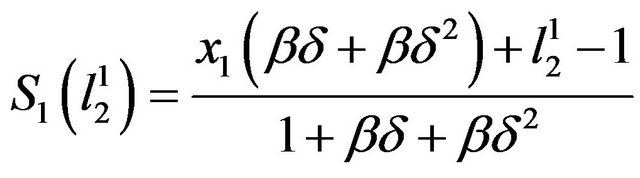(6)

The individual will choose in period 1 an intention of his period-2 leisure, 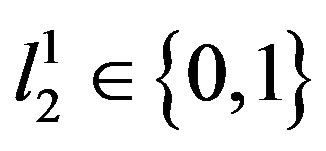, in order to maximize his well-being from the perspective of period 1. Therefore, he will plan to be working during period 2 if

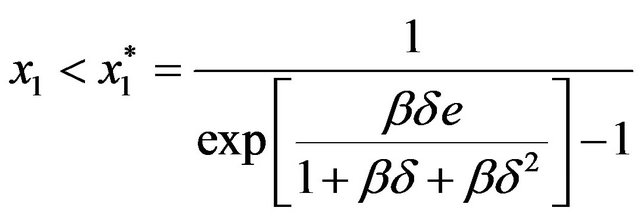(7)

Otherwise, he will intend to be retired during period 2.

2.2. Optimization in Period 2

Given, which is dependent on whether the individual intended to work or to be retired during period 2 from the perspective of period 1, the individual will select the consumption allocations from the perspective of period 2

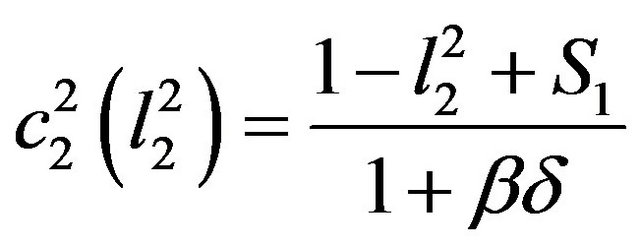(8)

and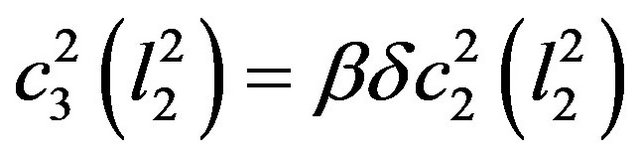. Note that these allocations are both dependent on the individual’s choice to actually work or to be retired during period 2, meaning that the individual will also choose to maximize his intertemporal utility from the perspective of period 2. Therefore, the representative individual will choose to actually work during period 2 if

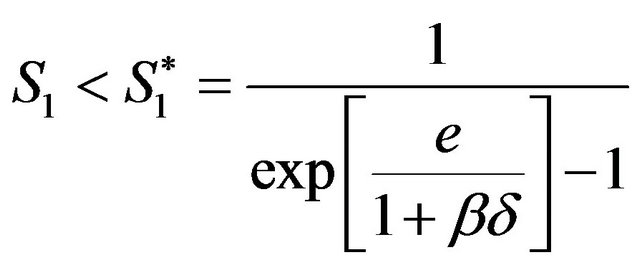(9)

where 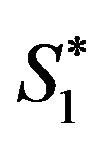is the threshold level of saving that is required to finance retirement during periods 2 and 3.

2.3. Time-Inconsistent Retirement Timing

2.3.1. The Existence of Planned Normal Retirement and Actual Early Retirement

We first study whether or not the possibility can exist for the individual to initially plan on working in period 2 from the perspective of period 1, and then reverse his original plan by actually retiring when period 2 arrives. The normal retirement intention will occur if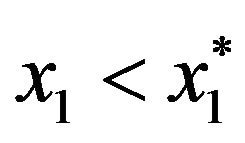, but the individual will actually choose to be retired when period 2 arrives if. The latter of these two inequalities is equivalent to

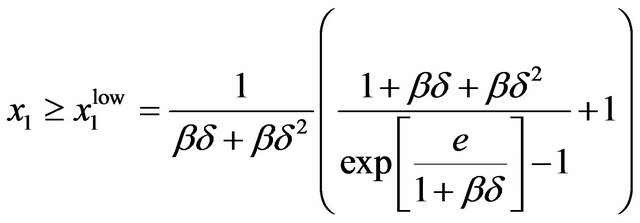(10)

where 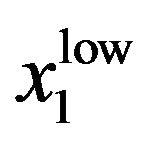is the lower-bound value for period-1 cash on hand that would enable savings from period 1 to be high enough to finance retirement during period 2, even though the individual had intended on normal retirement from the perspective of period 1. Holmes [2] analytically demonstrates that given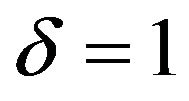, meaning that the retirement decision must be time-consistent with unit labor income in period 1 and with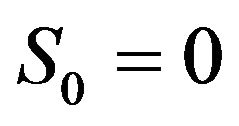. We find parameters 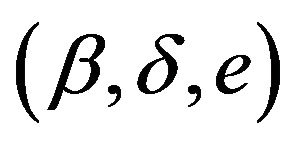with such that.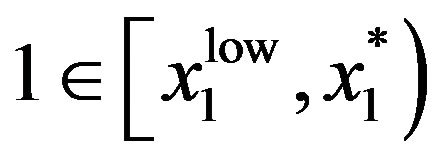

This indicates that time-inconsistent retirement timing can exist for the special case of unit labor income and a zero initial savings account balance, if long-term patience is entertained.^6,7 However, we are primarily interested in examining parameterizations with. From (7) and (10),

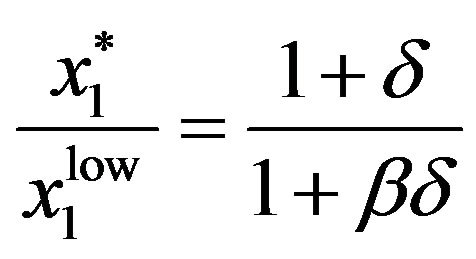(11)

as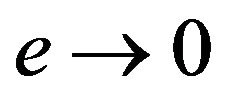, meaning that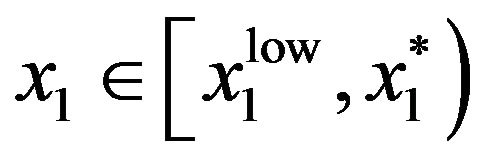must exist if.

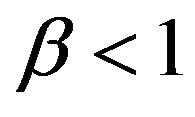This highlights the existence of time-inconsistent early retirement when initial assets are non-zero and/or if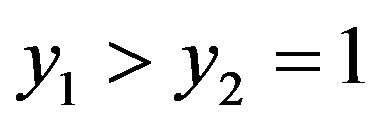. Yet, time-inconsistent retirement can also exist for larger values of, such as, and 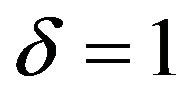which yields.

2.3.2. The Impossibility of Planned Early Retirement and Actual Normal Retirement

We now examine whether or not it is possible for the individual to intend to be retired during period 2 from the perspective of period 1, and then reverse his original intention by delaying retirement and actually working during period 2. An early retirement intention will occur if, but the individual will actually end up working during period 2 if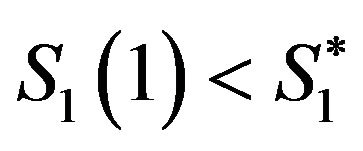. This implies

(12)

where 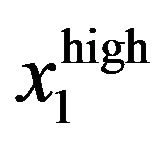is the upper-bound value for period-1 cash on hand that would lead to insufficient savings in period 1 such that the individual cannot finance retirement when period 2 arrives, even though period-2 retirement was the intention from the perspective of period 1. We formally state our finding for this case.

Proposition. The following sequence of retirement timing is impossible: 1) The individual initially plans to be retired in period 2 from the perspective of period 1; and then, 2) The individual actually chooses to work during period 2.

Proof. The ratio of (7) to (12) can be mathematically arranged as

(13)

where

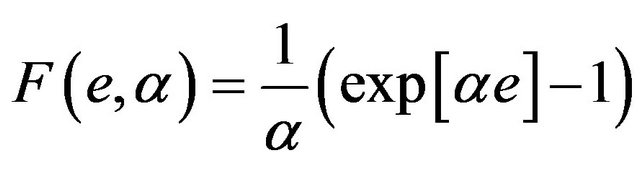(14)

Given, the first multiplicative term in (13) is greater than 1 if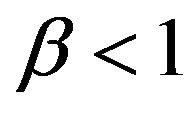. The second term is also greater than 1 on account that 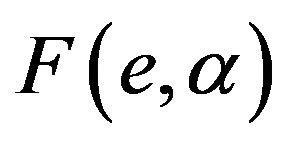is increasing in 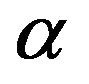for and given

under the same conditions on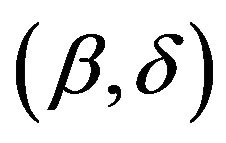. Thus, for all in the parameter space, meaning that (12) can never be satisfied. ■

3. Summary

The retirement decision is one of the most important choices that an individual can make during his lifetime, since the timing of retirement determines the life-cycle budget constraint to a large degree. Holmes [2] shows that hyperbolic discounting yields only time-consistent choices about the timing of retirement in a stylized threeperiod life-cycle model, despite time inconsistency along the consumption and saving margins. We build upon the three-period life-cycle framework of Diamond and Kőszegi [1] and Holmes [2] by working with more general assumptions about initial income and assets, and we establish the existence of time-inconsistent retirement timing. More specifically, we find that it is possible for the use of a quasi-hyperbolic discount function to induce an individual to retire earlier than what was initially planned. This is important given the vast array of research in public economics and in macroeconomics that uses three-period life-cycle/overlapping-generations models to study the effects of government policies on retirement.

Findley and Caliendo [13] show that it is also possible for an individual to delay retirement relative to previous retirement plans in a model that is set in continuous time with true hyperbolic discounting. Since we demonstrate analytically that this particular type of time-inconsistent (delayed) retirement timing is impossible given the coarse three-period time grid of the model in this manuscript, it remains an open question as to how a discrete-time threeperiod model with quasi-hyperbolic discounting would need to be modified to obtain delayed retirement timing. One possibility might be to model labor supply as a continuous choice during the second period of the life cycle, suggesting that actual retirement would occur at the exact moment during period 2 when leisure equals unity. We leave this question for future work.

4. Acknowledgements

We acknowledge and thank Nick Guo, Frank Caliendo, and two anonymous referees for helpful comments and suggestions.

REFERENCES

NOTES

¹See Ainslie and Haslam [3], Rachlin, Raineri, and Cross [4], Kirby and Maraković [5], Myerson and Green [6], and Madden and Johnson [7] for some examples and for an overview. Some studies alternatively find little or no evidence of hyperbolic discounting. For example, see Sutter, Kocher, Glätzle-Rüetzler, and Trautmann [8], and Dohmen, Falk, Huffman, and Sunde [9].

²Hyperbolic discounting is often studied using a quasi-hyperbolic approximation. See Laibson [10] for a brief overview.

³Tanaka and Murooka [12] provide an overview of the research in economics on hyperbolic discounting and saving outcomes.

⁴The existing empirical evidence on retirement expectations compared to realizations is sparse. Bernheim [14], Benítez-Silva and Dwyer [15], and Benítez-Silva, Dwyer, Gayle, and Muench [16] examine data from the Retirement History Survey (RHS) and the Health and Retirement Study (HRS) to conclude that the timing of retirement is time-consistent. These longitudinal surveys track the retirement expectations and realizations of individuals over a timeframe of approximately ten years. Yet, the ages of participants in the first wave of each survey were 58 to 63 years old in the RHS and 51 to 61 years old in the HRS. Therefore, time inconsistency in the retirement decision cannot be ruled out from the perspectives of earlier ages in the life cycle, given that retirement expectations were not measured at such ages in these two data sets.

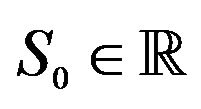⁵In general, , where is the initial condition on the asset account balance (from bequests received and/or from savings in previous periods which is not explicitly modeled here) and 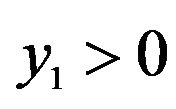is labor income in period 1. We are agnostic about the specific composition of cash on hand since it is inconsequential. Holmes [2] studies the nested case of S₀ = 0 and y₁ = 1.

⁶For example, given, , and. The corresponding discount function values are: from the perspective of period 1, and 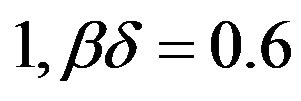from the perspective of period 2. Assuming that one period corresponds to 20 years of the life cycle, the corresponding short-term discount rate is 4.7% per annum while the long-term discount rate is (2.0% per annum. Both of these implied discount rates in tandem satisfy the spirit of hyperbolic discounting in which the discount rate declines in the delay.

⁷Calibrations of dynamic general-equilibrium models periodically yield when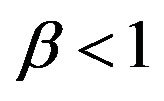. See İmrohoroğlu, İmrohoroğlu, and Joines [17] and Fehr, Habermann, and Kindermann [18] as examples.