ABSTRACT

Roles of emotion in decision-making have been attracting attention in neuroeconomics and behavioral game theory. We mathematically demonstrate that “emotion interference”, a recently-discovered psychological phenomenon [1] helps to solve social dilemma in a one-shot prisoner’s dilemma game. Furthermore, the present theory also accounts for the violation of Savage’s sure-thing principle in the prisoner’s dilemma [2]. Furthermore, it is also explained that why people in the society with higher social mobility are more cooperative. Relations of the present work to recently evolving fields of neuroeconomics and quantum decision theory are discussed.

1. Introduction

Even selfish agents often cooperate to their mutual benefit. However, why cooperation emerges is hard to solve. To address this question, the Prisoner’s Dilemma game has been utilized as a simple model problem [3]. In order to account for human’s tendency to cooperate in the Prisoner’s Dilemma (PD) game, several factors have been incorporated. For instance, punishment [4], reciprocity [3,5,6] and reputation [7] have been shown to increase cooperation in the PD. However, to date, little is known regarding how to solve social dilemma in the PD without introducing these social/societal devices. This issue is puzzling, because even in one-shot anonymous situations, non-negligible portions of people cooperate [8,9]. Regarding the non-social factors enhancing cooperation in the PD, Shafir and Tversky [2] reported that in a one-shot PD game many participants compete when they know their opponent has competed and also when they know their opponent has cooperated, but cooperate when they do not know their opponent’s response. This psychological phenomenon is referred to as the “disjunction effect”, which indicates that people violate the Surething principle proposed for the criterion of rational decision making [10]. The violation of the sure-thing princeple in the PD increases cooperation when people do not know whether the opponent is a cooperator or not, without introducing the social devices such as punishment, reputation, and/or reciprocity (see [9] for a recent replication of this effect). This psychological bias, the disjunction effect, may enhance mutual cooperation in societies with high degrees of social mobility where people do not know whether opponents are cooperative or not, which has been a puzzling societal phenomenon [11]. Although recent investigations in mathematical psychology attempt to model this with quantum probability theory [12-14], it is still unknown regarding what psychological processes induce the violation of the sure-thing principle in the prisoner’s dilemma game.

Recent years witnessed a rapid growth of interest in the roles of emotions in behavioral economics and neuroeconomics of human behaviors in game theoretic situations. By utilizing neuroscientific tools, several studies revealed that emotion plays a pivotal role in the rejection of unfair offers in the ultimatum game [15,16], the impunity game [17] and cooperation in the prisoner’s dilemma game [18]. However, little is known what type of mathematical characteristics of emotion induces cooperation in the PD. In the present study, we propose a theory of cooperation in the one-shot anonymous PD game, by incorporating the “emotion interference” effect, which has recently been discovered in a behavioral economic study [1]. By incorporating the emotion interference effect, we can generalize the expected utility theory for decision under risk and uncertainty [19] so that the new theory of “emotional expected utility” may capture the emotion interference effect discovered by [1]. The advantages of the present theory are 1) it can account for cooperation in the PD under the one-shot anonymous condition, 2) it can identify the psychological process underlying the violation of the sure-thing principle in the PD, and 3) it can explain why an increase in the numerical difference between the best outcome and the worst outcome reduces cooperation in the PD [20].

This paper is organized in the following manner. In Section 2, I briefly introduce the emotion interference (i.e., a type of emotional response under the disjunction condition). In Section 3, how the emotion interference effect solves social dilemma in the PD is explained by introducing a generalized expected utility theory (“expected emotional utility theory”). In Section 4, the implications of the present theory for future studies in behavioral economics and neuroeconomics are discussed.

2. Emotion Interference Effect under Disjunction Conditions

A recent study in behavioral economics reported that people felt less happy under the uncertain condition than under certainly good or bad conditions [1]. In the study, Wang and colleagues presented the following scenario: Imagine that you have completed your application for admission to two Ivy League universities, University A and University B. Although A and B are both on your list of DREAM universities for college, University A is much better than University B. At this time, you have received your offer to study at University B. You need to decide whether or not to accept the offer before the end of the semester; otherwise, your offer will expire.

1) You find out that you have been accepted by University A before the end of the semester;

2) You find out that you have been rejected by University A before the end of the semester;

3) You do not know whether you have been accepted or rejected by University A before the end of the semester.

After reading the scenario, the subjects were asked to indicate the degree to which they would be happy on a 9-point Likert scale (1 = not at all happy; 9 = very happy). Interestingly, the results indicated that the subjects were significantly less happy in condition III than conditions I and II. This psychological tendency (“emotion interfereence”, hereafter) violates both expected utility theory [19] and Kahneman-Tversky’s prospect theory [21], because no probability weighting function can account for this effect. In von Neumann-Morgenstern’s expected utility theory, the subjective value of lottery (where pi is a probability of obtaining outcome xi, I = 1, 2. Note that p1 + p2 = 1). Let us now incorporate the emotion interference effect in to the expected utility theory. We can do this by setting the subjective value of the lottery is the expected emotional utility: 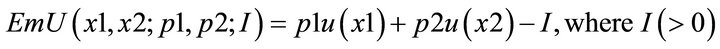indicates the effect of emotional response (emotion interference) under uncertainty (disjunction condition). Note that the value of emotion interference I depends on the type of the disjunction conditions. In the next section, we will see how the introduction of this term I solves social dilemma in the PD game.

3. Emotional Interference and Social Cooperation in the Prisoner’s Dilemma Game

The PD game is a classic model in game theory for the studies of the emergence of cooperation [3]. In a typical one-shot anonymous PD game, two agents each independently decide, without communication or reciprocation, whether to cooperate (C) or defect (D). The agents receive individual payoffs depending on the actions both independently taken. The payoff matrix in the PD is presented in Figure 1. The payoff for mutual cooperation b is the cooperation benefit. The payoff for mutual defection c is the (costly) defection payoff. In order for the payoff matrix of the game to be considered prisoner’s dilemma, it must obey the following pair of inequalities:

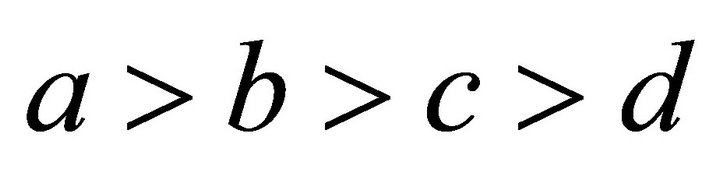(1)

. (2)

It is well-known that in the one-shot PD game, rational strategy is to (purely) defect for both of the agents which yields the Nash equilibrium of which is Pareto inferior to. In this section, we will demonstrate that incorporating the emotional interference effect into von Neumann-Morgenstern’s expected utility theory yields Pareto superior equilibrium in the Prisoner’s Dilemma.

Let vectors 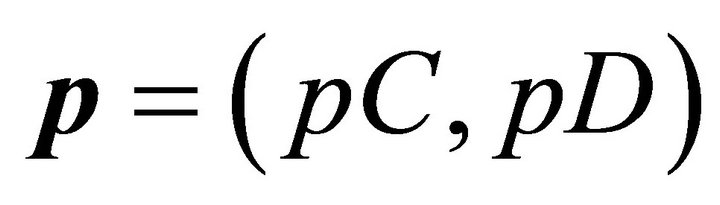and 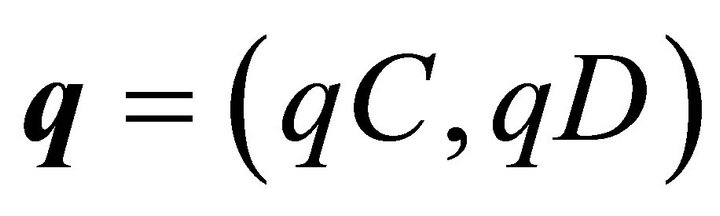be player 1 and 2’s mixed strategies. Then, the emotional expected utility (including the emotional interference term) for player 1 is:

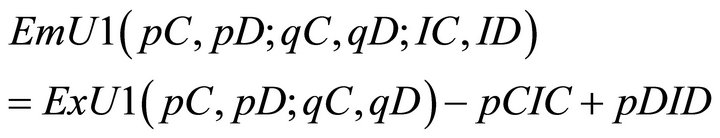(3)

where IC and ID > 0 are emotional interference effects when player cooperate and defect, respectively. As noted above, IC and ID are not necessarily the same, depending on whether player 1 cooperates or not. By simple calculations (utilizing the probability relation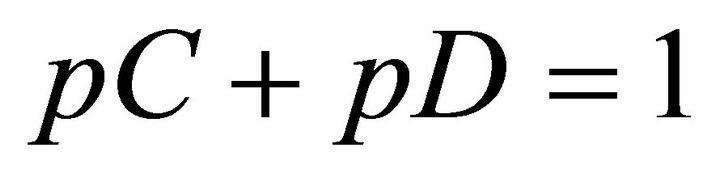), we obtain:

(4)

For player 1 to have mixed strategy with 0 < pC < 1, the following equation should hold:

(5)

which is equivalent to

. (6)

Note that qC can be withi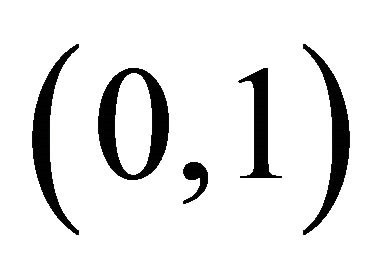n when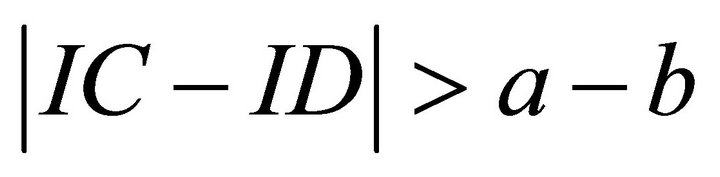, which indicates that there is a mixed strategy equilibrium. It is further to be noticed that when there is no emotion interference (i.e., IC = ID = 0) or emotion interference terms of cooperation and defection conditions are equal (IC = ID, i.e., fear and betrayal aversion are at the same degrees), there is only pure strategy Nash equilibrium of mutual defection. Together, we have demonstrated that emotion interference effect help to solve social dilemma in one-shot PD game (i.e., increaseing cooperation probability). The present theory also accounts for the violation of the sure-thing principle in the PD [2]; emotional interference (enhancing cooperation) only emerges when there is uncertainty in the opponent’s choice. This may also explain why people in the society with high degree of social mobility (high social uncertainty) are cooperative in comparison to that with low degree of social mobility and uncertainty [11].

4. Implications for Behavioral Neuroeconomics Theory

This study is the first to mathematically demonstrate that emotion interference effect, a recently-discovered psychological effect, solves social dilemma, at least in the PD. As noted in earlier, in a rapidly evolving field of neuroeconomics, roles of emotion in the decision in the PD have been examined with neuroimaging [18]. Future mathematical modeling studies of human cooperation should consider these findings from neuroimaging with the utilization of the present emotional expected utility theory. Furthermore, several types of psychologycal interference effects have recently been investigated within the frameworks of quantum probability theory [12-14]. In the future theoretical work of the emergency of cooperation should also explore the possibility of modeling the emotion interference effect with quantum formalism.

REFERENCES