Theoretical Economics Letters
Vol.2 No.1(2012), Article ID:17354,5 pages DOI:10.4236/tel.2012.21007
The Effect of Prices on Risk Aversion
1University of Canterbury, Christchurch, New Zealand
2Universidad Autónoma de Madrid, Madrid, Spain
Email: richard.watt@canterbury.ac.nz, franciscojose.vazquez@uam.es
Received November 6, 2011; revised December 16, 2011; accepted December 22, 2011
Keywords: Risk Aversion; Prices; Indirect Utility
ABSTRACT
Traditionally, risk aversion (both absolute and relative) has been expressed as a function of wealth alone. The characteristics of risk aversion as wealth changes have been extensively studied. However, prices, as well as wealth, enter the indirect utility function, from which the typical risk aversion measures are calculated. Given that, changes in prices will affect risk aversion, although exactly how has not been considered in the literature. This paper provides such an analysis. In particular, we firstly remind the reader that both absolute and relative risk aversion are homogeneous functions, and as such independently of their particular slopes in wealth, there is a natural effect that holds relative risk aversion constant and decreases absolute risk aversion when prices and wealth are increased by a common factor. We also show that the size of relative risk aversion as compared to the number 1, which is of much importance to the comparative statics of the economics of risk and uncertainty, depends on how changes in prices affect marginal utility. Under plausible (and standard) theoretical assumptions we find that relative risk aversion is likely to be increasing, and that increases in prices will have a tempering effect on risk aversion.
1. Introduction
Risk aversion is one of the most useful concepts in the microeconomics of risk and uncertainty. In all standard analyses, risk aversion is measured by the ratio of the second derivative of indirect utility with respect to wealth divided by its first derivative (also with respect to wealth) and multiplied by –1 (the well-known ArrowPratt measure of absolute risk aversion). However, indirect utility is a function of both wealth and the price vector of consumption goods and services. Of course the derivatives of indirect utility with respect to wealth necessarily hold prices constant, but changes in prices will affect indirect utility and thus will also affect risk aversion. To the best of our knowledge, this effect has not been studied in the existing literature.
In particular, relative risk aversion is an extremely useful concept in microeconomics, both because it is the elasticity of marginal utility, and because it is reasonably easy to get empirical estimations of it. Indeed, in many analyses, it becomes important whether or not relative risk aversion is greater than, less than, or equal to 1. Nobel laureate Ken Arrow [1] argued (convincingly, but without formal proof) that for reasonable values of wealth, relative risk aversion should be greater than 1 and increasing, something that is very often found to be so in empirical studies.1 Also, a good deal of comparative statics results (see, for example, the literature on the simultaneous choice of insurance and risk; [2-4]) only go through for the case of relative risk aversion less than 1. In this paper the relationship between relative risk aversion and the number 1 is reconsidered taking into account explicitly the effect of prices as well as wealth.
2. Risk Aversion in a Classic Demand Setting
Given that we will be using the idea of the indirect utility function, let us define things using the following (standard) notation. Let u(x) denote the direct utility function, where 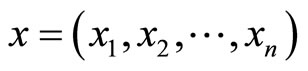 is the commodity vector. We assume that u(x) is strictly increasing in each xi and concave in the vector x. Let
is the commodity vector. We assume that u(x) is strictly increasing in each xi and concave in the vector x. Let 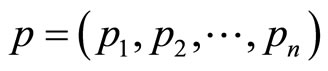 denote the vector of commodity prices (all, of course, strictly positive). The consumer’s wealth, which is the maximum value of financial resources available for consumption, is given by w. The optimal demand is given by
denote the vector of commodity prices (all, of course, strictly positive). The consumer’s wealth, which is the maximum value of financial resources available for consumption, is given by w. The optimal demand is given by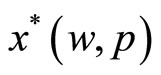 . Substituting the optimal demand into the direct utility function gives us the indirect utility function;
. Substituting the optimal demand into the direct utility function gives us the indirect utility function;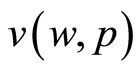
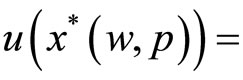 .
.
Using this notation, the Arrow-Pratt measure of absolute risk aversion is defined as: and the Arrow-Pratt measure of relative risk aversion is defined as
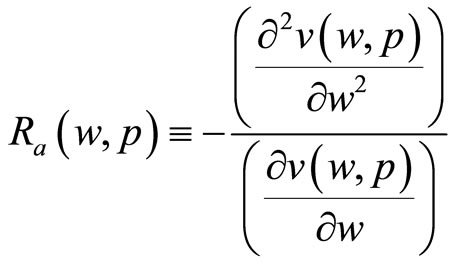
and the Arrow-Pratt measure of relative risk aversion is defined as
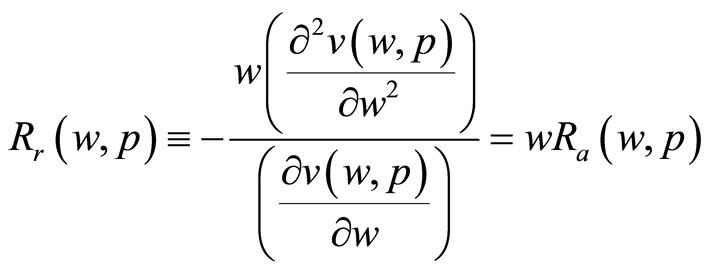
In these two definitions we have explicitly recognized the dependence of risk aversion on the price vector, something that is not typically done, since normally risk analysis is carried out under an assumption of constant prices.
In all that follows, we assume that u(x) is strictly concave in x, so that indirect utility is concave in w (i.e. the individual is risk averse in the standard sense) and we assume that the consumption solution is strictly interior in all goods .
.
We begin by noting a couple of useful (and well known) lemmas:2
Lemma 1: Absolute risk aversion is homogeneous of degree –1 in (w,p).
From lemma 1, if all prices and wealth increase in a given proportion, say α, which is neither 0 nor 1, then absolute risk aversion will increase in the proportion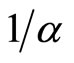 , which of course implies that it moves in the opposite direction to the change in prices and wealth. Thus even though a common proportional increase in prices and wealth will not affect the optimal consumption purchase, or the level of utility in the optimum, it will decrease risk aversion. For example, in economies with an inflation rate that increases all prices and incomes in the same proportion, we would expect that over time all individuals suffer lower and lower risk aversion.
, which of course implies that it moves in the opposite direction to the change in prices and wealth. Thus even though a common proportional increase in prices and wealth will not affect the optimal consumption purchase, or the level of utility in the optimum, it will decrease risk aversion. For example, in economies with an inflation rate that increases all prices and incomes in the same proportion, we would expect that over time all individuals suffer lower and lower risk aversion.
Note that lemma 1 has nothing to do with the often assumed characteristic of decreasing absolute risk aversion (DARA), which is when absolute risk aversion decreases with increases in wealth alone. Even if absolute risk aversion were constant (or increasing) in w, it would still decrease with simultaneous proportional increases in all prices and w. This is something that perhaps should be taken into account when experimental data on risk aversion is taken—field work that is directed toward seeing how increases in w over time affect risk aversion should check that the only increases over time were in w, since if prices increased also there would be an effect that would decrease risk aversion even though risk aversion were not necessarily decreasing in w.
Lemma 2: Relative risk aversion is homogeneous of degree 0 in (w, p).
Again, the homogeneity of degree 0 of relative risk aversion may lead empirical field-work to conclude that relative risk aversion is likely to be quite constant in w even when it need not be so. If prices increase along with wealth, then any utility function will return constant relative risk aversion.
3. Relative Risk Aversion
Under plausible (and standard) theoretical assumptions Ken Arrow (see Arrow, 1971) argued without proof that relative risk aversion should be greater than 1 for sufficiently large levels of wealth and increasing. Here we show that this is indeed the case, and furthermore, the relationship between relative risk aversion and the number 1 is intimately related to the effect of price on risk aversion.
Proposition 1: Relative risk aversion can be expressed as the sum of the number 1 and the summation of the elasticity of marginal utility with respect to all prices:  , where
, where
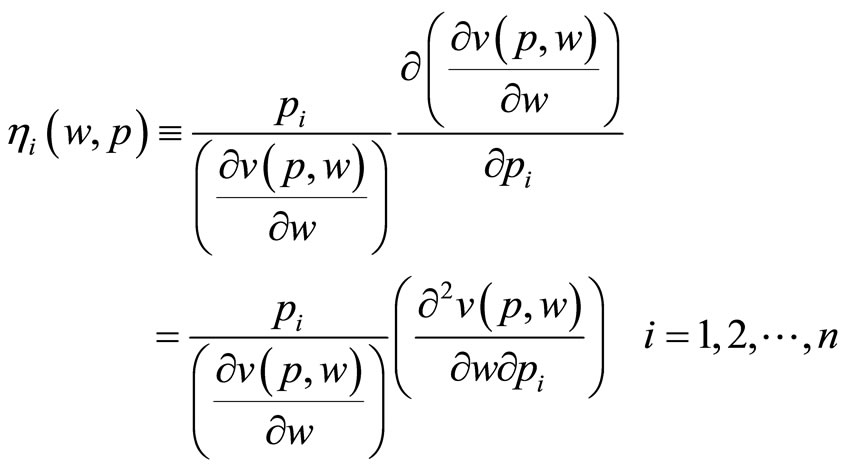
Proof. From basic consumer theory, the effect of an increase in a price upon indirect utility is
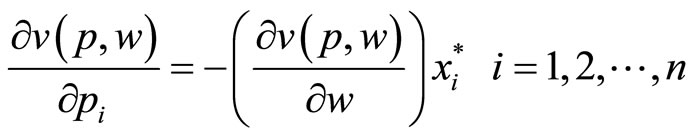
Directly rearranging, we get Roy’s Identity:

Now, derive this expression with respect to w to get:
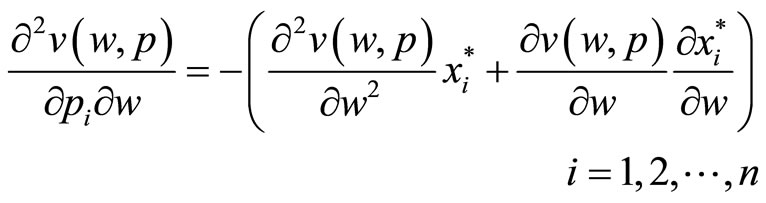
From Young’s theorem, the order of derivatives on the left-hand-side is irrelevant, so this can be written as

Now, multiply by pi, and divide by 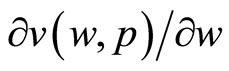 to get
to get
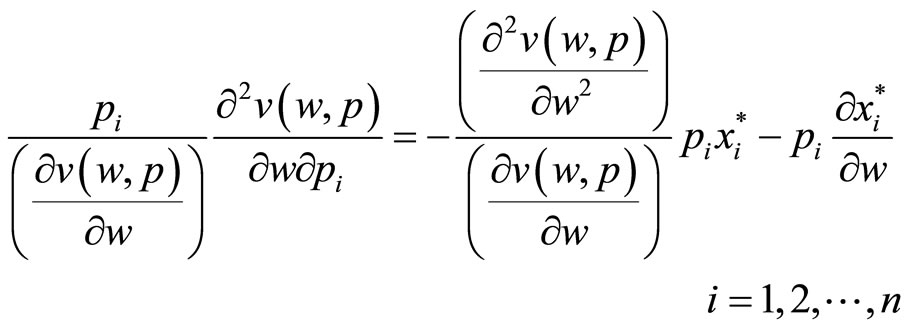
Denoting the elasticity of marginal utility of wealth with respect to the i th price by  , we have
, we have
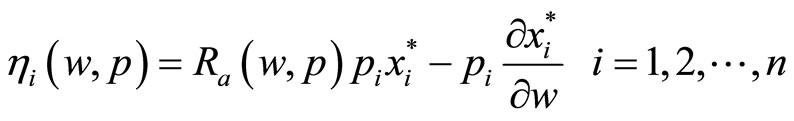
and finally sum over all n (recalling that  and
and 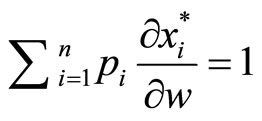 that ) to get the result:
that ) to get the result:
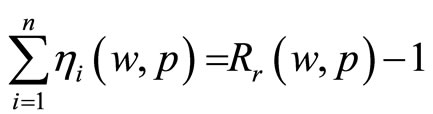
Q.E.D.
So the Arrow-Pratt measure of relative risk aversion can be expressed as the number 1 plus a summation of elasticities. Thus the relationship between relative risk aversion and the number 1 implies that we are interested in the relationship between 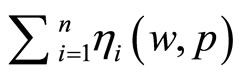 and the number 0. In turn, whether or not the summation of elasticities is greater than or less than 0 reduces to thinking about how the marginal utility of wealth is affected by an increase in any given price of the final goods that are consumed in the end, i.e. if the second order derivative
and the number 0. In turn, whether or not the summation of elasticities is greater than or less than 0 reduces to thinking about how the marginal utility of wealth is affected by an increase in any given price of the final goods that are consumed in the end, i.e. if the second order derivative  is positive or negative (or equal to 0).
is positive or negative (or equal to 0).
That is, should a rise in a price make an extra unit of wealth more or less valuable in utility terms? If the marginal utility of wealth were to be decreased by an increase in any particular price, then relative risk aversion would be less than 1. If price increases raise the marginal utility of wealth, then relative risk aversion is greater than 1, and if some price rises increase marginal utility of wealth, and others decrease it, then anything is possible. In this section, some logical hypothesis are offered that may help to decide the issue.
It is logical to assume that the sign of 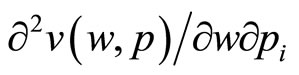 is the same for all goods, and for that reason, we now add a new assumption:
is the same for all goods, and for that reason, we now add a new assumption:
Assumption 1:
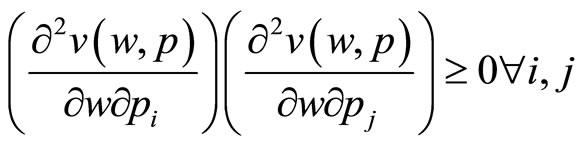
Also, we can choose our utility units such that 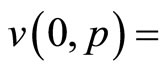
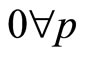 , that is, with no wealth (and thus no consumption), the consumer achieves no utility. But then, since the utility function must shift vertically downwards with the increase in any price, if
, that is, with no wealth (and thus no consumption), the consumer achieves no utility. But then, since the utility function must shift vertically downwards with the increase in any price, if 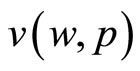 is to satisfy the three requisites of positive slope, concavity, and
is to satisfy the three requisites of positive slope, concavity, and  , then it becomes necessary for the graph with the higher price to be less steep, at least for very small values of w, than the graph with the lower price. That is:
, then it becomes necessary for the graph with the higher price to be less steep, at least for very small values of w, than the graph with the lower price. That is:
Proposition 2: There must exist a range of sufficiently small values of w for which 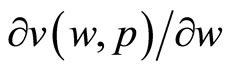 is decreasing in pi, that is
is decreasing in pi, that is  .
.
Proof. Assume that 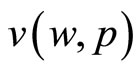 is a C2 function (i.e. it is continuous with continuous first and second derivatives) such that
is a C2 function (i.e. it is continuous with continuous first and second derivatives) such that  and
and 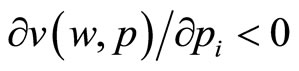 for every i = 1, 2, …, n. Firstly note that we can write
for every i = 1, 2, …, n. Firstly note that we can write  in the following way:
in the following way:

Now, take 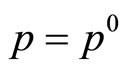 and
and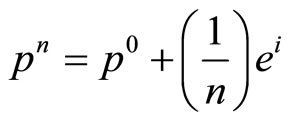 , where
, where
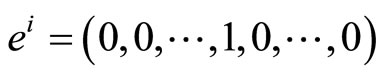 , that is the vector whose components are all 0 except for the i th component which is 1. Then write:
, that is the vector whose components are all 0 except for the i th component which is 1. Then write:
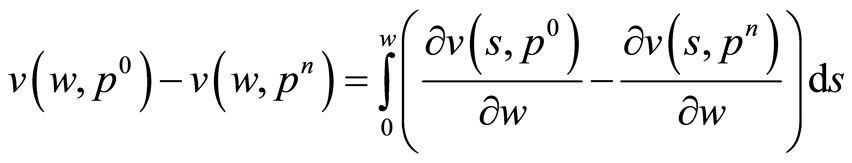
Using Cauchy’s intermediate value theorem, we have:
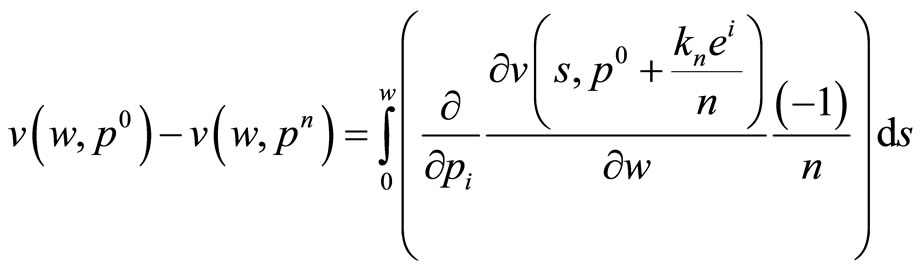
where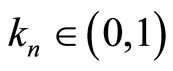 . By hypothesis, the previous equation is positive for all values of
. By hypothesis, the previous equation is positive for all values of  and
and 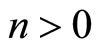 , which implies that
, which implies that
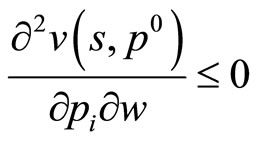
for every 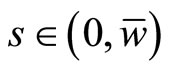 for some
for some 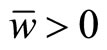 . Therefore,
. Therefore, 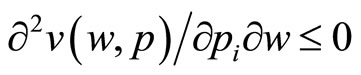 for small enough values of w.
for small enough values of w.
Q.E.D.
Thus, under assumption 1, it holds that 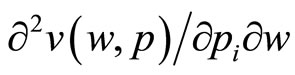
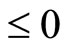 for sure when w is quite small, and so we can conclude that for small enough values of w we have
for sure when w is quite small, and so we can conclude that for small enough values of w we have 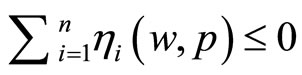 , and so
, and so 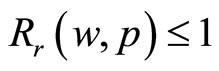 .
.
Secondly, we also assume (as did Arrow) that utility is bounded above, that is, as wealth gets infinitely large, utility remains finite.
Assumption 2: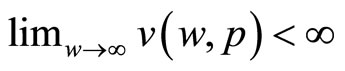 .
.
We add to that the following;
Assumption 3: 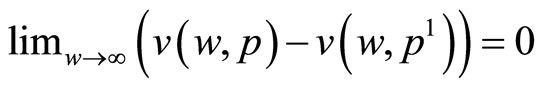 .
.
This assumption implies that marginal price rises do not affect utility as wealth gets infinitely large, so that infinitely wealthy individuals are not concerned with small price rises. Under assumptions 2 and 3, when two utility functions are drawn, the only difference between them being that the lower one has a greater value of the I th price, then at high enough values of w, the two curves would approach each other again. Mathematically, it would have to hold that 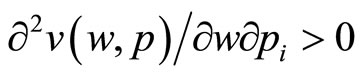 at high values of w:
at high values of w:
Proposition 3: If utility is bounded from above at some positive bound that is common to all price levels, then if w is sufficiently high we have 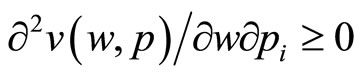 .
.
Proof. Define , and
, and 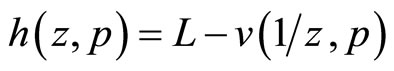 , for
, for . We assume that
. We assume that 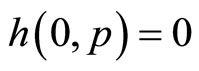 (i.e.
(i.e. 
tends to L) for all p, and that 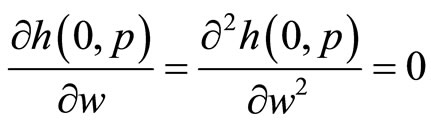
for all p. We assume that is a C2 function. Now, following the same steps as in the previous proposition, we can write:
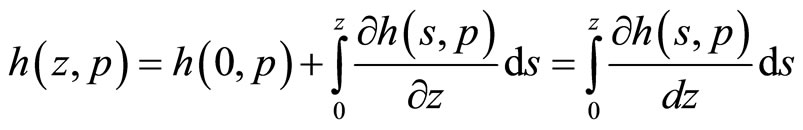
Now, again take 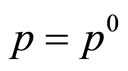 and
and  , where
, where 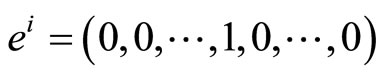 , that is the vector whose components are all 0 except for the i th component which is 1. Then we get:
, that is the vector whose components are all 0 except for the i th component which is 1. Then we get:

From Cauchy’s intermediate value theorem, we then have:

where 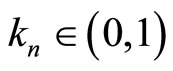 . But, using the above definition of, this is:
. But, using the above definition of, this is:

By hypothesis, this last equation is negative for all values of 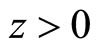 and
and 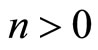 , which implies that
, which implies that
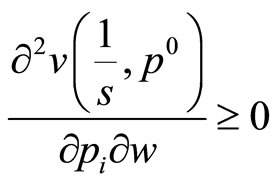
for every 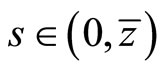 for some
for some  . Therefore, we get
. Therefore, we get  for large enough values of w.
for large enough values of w.
Q.E.D.
Thus, assumptions 2 and 3, together with assumption 1, gives us the result that at high enough values of wealth we get , and
, and .
.
Naturally, if relative risk aversion is monotone in wealth (as is normally assumed), then from Propositions 2 and 3, we have the result that relative risk aversion is increasing in wealth, as Arrow hypothesized.
Furthermore, note that we now have an even more interesting implication. Given our three assumptions, certain uniformity assumptions on how the indirect utility curve moves downwards with price increases lead directly to the result that the indirect utility function gets less and less concave (i.e. more and more linear) in wealth as a price rises. That is, absolute risk aversion would be decreasing in prices. This is curious, since an increase in a price has two effects—the substitution effect (consumption is substituted away from the more expensive good), and the wealth effect which is equivalent to a decrease in wealth. So if absolute risk aversion is decreasing in w, it is natural to think that increases in price, which imply a certain effect of wealth decreases, would lead to greater risk aversion. But we find here evidence for the opposite.3
4. Conclusions
In this paper we have considered the effect of prices upon risk aversion. While the effect of wealth upon risk aversion is very well understood, it seems curious that no analysis of the effects of prices has been done, given that the indirect utility function is a function of both wealth and the price vector. Firstly, we have shown that both absolute and relative risk aversion are homogeneous functions, and as such independently of their particular slopes in wealth, there is a natural effect that holds relative risk aversion constant and decreases absolute risk aversion when prices and wealth are increased by a common factor. This implies that when field data is used to measure the effect of wealth upon risk aversion, it is very important to control for price effects.
Secondly, we show that the size of relative risk aversion as compared to the number 1, which is of much importance to the comparative statics of the economics of risk and uncertainty, depends on how changes in prices affect marginal utility. Under plausible (and standard) theoretical assumptions we prove that relative risk aversion is less than 1 for sufficiently small levels of wealth, and greater than 1 for sufficiently large levels of wealth. This is, of course, theoretical evidence that points directly toward increasing relative risk aversion being a general characteristic of utility.
Finally, the analysis suggests that increases in prices will have a tempering effect on risk aversion, which is indeed rather counter-intuitive, since increases in price are associated with decreases in real-wealth, something that might well suggest increases in risk aversion (under DARA).
5. Acknowledgements
F. Vázquez thanks the Secretaría de Estado de Universidades e InvestigacióndelMinisterio de Educación y Ciencia for financial support.
REFERENCES
- K. Arrow, “Essays in the Theory of Risk Bearing,” Amsterdam, North Holland, 1971.
- L. Eeckhoudt, J. Meyer and M. Ormiston, “The Interaction between the Demands for Insurance and Insurable Assets,” Journal of Risk and Uncertainty, Vol. 14, No. 1, 1997, pp. 25-39. doi:10.1023/A:1007717719423
- D. Meyer and J. Meyer, “A More Reasonable Model of Insurance Demand,” In: C. D. Aliprantis, K. J. Arrow, P. Hammond, F. Kubler, H. M. Wu and N. C. Yannelis, Eds., Assets, Beliefs, and Equilibria in Economic Dynamics. Essays in Honor of Mordecai Kurz, Studies in Economic Theory, Vol. 18, Springer-Verlag, 2004, pp. 733-742.
- J. Meyer and M. Ormiston, “Demand for Insurance in a Portfolio Setting,” The Geneva Papers on Risk and Insurance Theory, Vol. 20, No. 2, 1995, pp. 203-211. doi:10.1007/BF01258397
NOTES
1Of course, as a first approximation economists (especially macroeconomists) often use the neperian log function for utility (indeed, the very first utility function, suggested by Daniel Bernoulli way back in 1738, was the neperian log function), which returns a constant degree of relative risk aversion equal to 1.
2Both lemmas are easy to prove, and in the interests of brevity, the proofs are not given here.
3The exact effect of an increase in a price upon risk aversion can, of course, be calculated by differentiation. However, performing this exercise is not particularly enlightening, as the final effect is a complex equation of higher order elasticities.

