Journal of Mathematical Finance
Vol.06 No.04(2016), Article ID:71225,18 pages
10.4236/jmf.2016.64043

On the Solution of the Multi-Asset Black-Scholes Model: Correlations, Eigenvalues and Geometry

Mauricio Contreras1, Alejandro Llanquihuén2, Marcelo Villena1

1Facultad de Ingeniería y Ciencias, Universidad Adolfo Ibáñez, Santiago, Chile

2Facultad de Ciencias Exactas, Universidad Andrés Bello, Santiago, Chile

Copyright © 2016 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

Received: August 23, 2016; Accepted: October 11, 2016; Published: October 14, 2016

ABSTRACT

In this paper, the multi-asset Black-Scholes model is studied in terms of the im- portance that the correlation parameter space (equivalent to an N dimensional hypercube) has in the solution of the pricing problem. It is shown that inside of this hypercube there is a surface, called the Kummer surface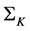, where the determinant of the correlation matrix 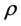is zero, so the usual formula for the propagator of the N asset Black-Scholes equation is no longer valid. Worse than that, in some regions outside this surface, the determinant of becomes negative, so the usual pro- pagator becomes complex and divergent. Thus the option pricing model is not well defined for these regions outside. 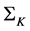On the Kummer surface instead, the rank of the 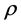matrix is a variable number. By using the Wei-Norman theorem, the pro- pagator over the variable rank surface 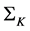for the general N asset case is computed. Finally, the three assets case and its implied geometry along the Kummer surface is also studied in detail.

Keywords:

Multi-Asset Black-Scholes Equation, Wei-Norman Theorem, Correlation Matrix Eigenvalues, Kummer Surface, Propagators

1. Introduction

Since the seminal work of Black, Scholes and Merton on option pricing, see [1] [2] , an important research agenda has been developed on the subject. This research has mainly centered in extending the basic Black and Scholes model to well known empirical regularities, with the hope of improving the predicting power for the famous formula, see for example [3] - [6] . An interesting extension has been the modeling of many underlying assets, which has been called the multi-asset Black-Scholes model [3] [7] . In this case, the option price satisfies a diffusion equation considering many related assets. The first work addressing this problem in the literature was Margrabe (1978), see [8] . The Margrabe formula considered an exchange option, which gives its owner the right, but not the obligation, to exchange b units of one asset into a unit of another asset at a specific point in time. Specifically, Margrabe derived a closed-form expression for the option by taking one of the underlying assets as a numeraire and then applying the Black and Scholes standard formulation. Later Stulz [9] found analytical formulae for European put and call options on the minimum or the maximum of two risky assets. In this particular case, the solution is expressed in terms of bivariate cumulative standard normal distributions, and when the strike price of the option is zero the value reduces to the Margrabe pricing. Other interesting papers that follow in this literature are [10] - [15] . The numerical implementation of the solution of the multi-asset Black-Scholes model is increasingly difficult for models with more that three assets, see for instance [16] - [18] . One important point, that has been missed in the literature, is that in all of the multi-asset Black-Scholes models mentioned above, the relationship between assets is modeled by their correlations, and hence it is implicitly assumed that a well behaved multivariate Gaussian distribution must exist in order to have a valid solution.

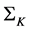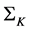In this paper, the multi-asset Black-Scholes model is studied in terms of the im- portance that the correlation parameter space (which is equivalent to an N dimensional hypercube) has in the solution of the option pricing problem. It is shown that inside of this hypercube there is a surface, called the Kummer surface [19] - [22] , where the determinant of the correlation matrix is zero, so over the usual formula for the propagator of the N asset Black-Scholes equation is no longer valid. Worse than that, outside this surface, there are points where the determinant of becomes negative, so the usual propagator becomes complex and divergent. Thus the option pricing model is not well defined for some regions outside. On 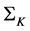the rank of 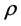matrix is a variable number, depending on which sector of the Kummer surface the correlation parameters are lying. By using the Wei-Norman theorem [23] - [26] , the propagator along the Kummer surface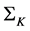, for the N assets case is found. This expression is valid whatever the value of the 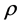matrix ranks over.

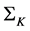This paper is organized as follows. Section 2 describes the traditional multi-asset Black-Scholes model. In Section 3, the problem is formulated as a N dimensional diffusion equation. In Section 4, the implied geometry of the correlation matrix space is analyzed, specially when its determinant is zero, which coincides with a Kummer surface in algebraic geometry. The Kummer surface and its geometry are reviewed for the particular case of three assets in Section 4.1. In Section 5, by using the Wei-Norman theorem the propagator over the variable rank surface for a general N asset case is computed. Finally, some conclusions and future research are presented in Section 6.

2. The Multi-Asset Black-Scholes Model

Consider a portfolio consisting of one option and N underlying assets. Let 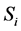be the price processes for the assets; where each asset satisfies the usual dynamic

(1)

and the Wiener processes are correlated according to

(2)

where is the symmetric matrix

(3)

so

(4)

If the price process for the option is, the value V of the portfolio is given by

(5)

where are the shares of each asset in the portfolio. The self-financing portfolio condition ensures that

(6)

and applying It Lemma for one gets

(7)

According to [4] , for a free arbitrage set of N assets, the return of the portfolio is

(8)

and from Equations (7) and (8) one has

(9)

Collecting and terms in the above equation one gets:

(10)

and

(11)

From Equation (11), and given the independence of the for

(12)

or equivalently

(13)

so one arrives at the multi-asset Black-Scholes equation

(14)

which must be integrated with the final condition

for constant r, , and a simple contingent claim.

3. The Multi-Asset Black-Scholes Equation as a N Dimensional Diffusion Equation

Here, some transformations are developed, which maps the multi-asset option pricing equation in a more simpler diffusion equation. If one makes the change of variables

(15)

in (14), one can map this equation to

At least if one defines as

(16)

then satisfies the equation

Now, by defining the variables

(17)

the above equation can be written as

And finally, by defining the forward time coordinate

(18)

one arrives at

(19)

Now performing the transformation

(20)

one can change the variables to the coordinates that diagonalizes the matrix

(21)

where

(22)

and U is the change basis matrix, with,. In this diagonal coordinate system, the diffusion equation read finally

(23)

Now this equation is studied in terms of the behavior of the eigenvalues.

4. The Geometry of the r Matrix

The matrix in (3) can be characterized completely for the dimen-

sional vector

(24)

which lies inside of an M dimensional hypercube centering in the origin and of length 2. Thus, the matrix is a function of:. Note that, for some point inside of the hypercube, the determinant of the matrix vanishes. For example, for the vertex

(25)

In fact, exists a whole surface inside the hypercube, where the determinant of vanishes. This surface, called Kummer surface in algebraic geometry [19] - [22] , is defined by the equation

(26)

In fact, one can think of the hypercube as the disjoint union of the subset of point or surfaces of constant C determinant value:

(27)

Let an arbitrary vector in and let the determinant of in each point, that is. Note that is a polynomial function in terms of the coordinates.

The vector given by the M dimensional gradient is perpendicular to the level surfaces and gives the direction for greater growth of the function. Note also that the components of this vector are also polynomial functions of the coordinates, so is a continuous vector function.

Consider now a point, that is,. As and are continuous, there is a neighbor of on, such that for the vector with, whereas the vector with, due to the function growths along the direction. Thus, the Kummer surface separates spacial regions with positive determinant from that with negative determinant.

In its diagonal form, Equation (26) is

(28)

where the, that is

(29)

Note that Equation (29) implies that there is at least one eigenvalue that is zero over all the Kummer surface. But on other eigenvalues can also become null. Thus, the Kummer surface is a variable rank surface.

As is equal to, the vector can be written as

(30)

Let say that is the zero eigenvalue over all Kummer surface. Then over, the vector is given by

(31)

If is the subregion of over which there are null eigenvalues, then by (31)

(32)

Thus higher order rank subregions of the Kummer surface are characterized by the fact that the vector vanishes on them.

Consider now, the origin where. It is easy to show that for points near to the origin, the function goes as by expanding in Taylor series around the origin and keeping the least order terms in the expansion. The vector near the origin is then and its an inward radial vector. So near the origin, the constant determinant surfaces are given approximately by M di- mensional spheres and growths inward to the origin.

Let a curve that starts in the origin and that is normal to all surfaces, that is, its tangent vector is parallel to the vector in each point. Because, near the origin the vector is radial, one can reach any point of the space starting from the origin using such a curve. Moving along in the outer direction, the function always decreases from its initial value 1. Thus, at some point in, the function vanishes. Thus means that the Kummer surface must contain a closed subsurface that enclosed the origin. Then inside of this closed subsurface the determinant of the matrix must be positive and outside there are points where the determinant of the correlation matrix is necessarily negative. Note that can be contained totally inside the hypercube or can cut it in different regions with positive or negative determinant values respectively.

Thus, outside there are regions where the determinant

(33)

so at least one of the eigenvalues must be negative outside. Inside however

(34)

This implies that pairs of eigenvalues can be negative. But inside the eigenvalue cannot be negative. To prove that, consider the origin where all eigenvalues are equal to one. When moves outward along a curve that start at the origin, each eigenvalue will change its value from its initial positive value 1, but cannot become negative. If for some points along inside of, then there is a point where. This implies that the vector would cross the surface, but it is impossible because is inside of where. Then inside the surface all eigenvalues of the correlation matrix are positive.

In order to grasp the above ideas in detail the case of three assets is studied in the next sub section.

The Geometry of the N = 3 Assets Case

The matrix, for the three assets case, is equal to

(35)

where the vector is written as. For this parameteri- zation the determinant of the matrix is

The constant determinant surfaces in the interior of the hypercube are shown in Figure 1, for some positive values between. Instead, in Figure 2, some surfaces for negative C values are displayed with.

The Kummer surface is given by the condition, that is

(36)

Figure 1. (a), (b), (c), (d), (e).

From (36) one found that the Kummer subsurface inside the hypercube is given by the parametric equations

(37)

Figure 3 shows the Kummer superior subsurface given by, the Kummer inferior subsurface given by and the complete Kummer subsurface.

Because separates a region with from that with and due to the origin the determinant is one, then inside of the determinant of the matrix must be positive, which is consistent with Figure 1. The region situated between and the cube has negative determinant in this case.

In terms of its diagonal form, the matrix inside or outside where, is

Figure 2. (a), (b), (c), (d), (e).

(38)

where the three eigenvalues, and when.

On the Kummer superior subsurface, the diagonal form of the matrix is

(39)

where

(40)

Figure 3. (a) Kummer superior subsurface, (b) Kummer in- ferior subsurface, (c) complete Kummer subsurface. Note that the Kummer subsurface is closed and its is completely inside the hypercube in this case. Thus the region between and the hypercube has negative determinant for the three assets system.

and

(41)

Figure 4 gives the eigenvalues and as functions of x and y.

For the Kummer inferior subsurface, the diagonal form of the matrix is instead

(42)

Figure 4. (a), (b).

where

(43)

and

(44)

Figure 5 gives the eigenvalues and as functions of x and y.

Note that the eigenvalues and are always greater than zero, but and are zero for the extreme values of the correlation parameter and. Figure 6 shows both eigenvalues and in the same graph. It is possible to see clearly that the proper value becomes equal to zero only for the extreme correlations value cases

(45)

which are the vertexes of the Kummer subsurface in Figure 3 or the four base points of Figure 6.

Thus, depending on which region of the three dimensional cube the vector is lying, the correlation matrix has two null eigenvalues, one null eigenvalue or it can be invertible. Thus the rank of the matrix changes when moves along the Kummer surface.

5. Pricing, the Wei-Norman Theorem, Propagators and SK

The problem of pricing the multi-asset option is now tackled by taking into account the geometrical properties of the correlation matrix analyzed in the Section 3. In order to do that one needs first to solve the Equation (23). For this, the Wei-Norman theorem [23] - [26] is applied. In this particular case this theorem estab- lishes that the solution of (23) can be writing as

(46)

Figure 5. (a), (b).

Figure 6. The eigenvalue as function of.

where

(47)

with

(48)

and

(49)

that is

(50)

by inserting N one dimensional Dirac’s deltas, one can write the above equation as

(51)

or as

(52)

where the propagator is defined by

(53)

with the N dimensional Dirac’s delta. Now using the Fourier expansion

(54)

the propagator can be written finally as the product

(55)

The Propagator Inside S0

When is inside of, all eigenvalues are positive, so the N integrations in (55) can be performed to give [27] [28]

(56)

or

(57)

By using transformations (15), (16), (17) and (18) one can write the propagator for the option price in the space as

(58)

with

(59)

which is the usual form of the propagator in the S space (see for example [3] [7] ). Note this form of the propagator is valid only when. So (58) can be applied inside the closed subsurface or some region between and the interior of the hypercube that verifies and have only positive eigenvalues.

6. The Propagator for the Kummer Surface SK

In this section, an expression for the propagator over the Kummer surface is obtained. It is assumed that a region of that has non zero eigenvalues and null eigenvalues. Due to it is on the surface, the Equation (26) implies that one of the coordinates of the vector, is determined by the other coordinates. These independent coordinates are called. Thus in this section, the vector is an M dimensional vector that depends on in- dependent coordinates. In this situation the propagator in (55) gives

(60)

By performing the integrations

(61)

If the N dimensional vector is separated in two parts as

(62)

the above propagator can be written in a more compact form as

(63)

where

(64)

is the reduced diagonal matrix on the Kummer surface. If one separates the vector in A and B components as

(65)

then relation (20) induces the transformation

(66)

where, , and are the matrices that result from sectioning into A and B components.

The quadratic term in the exponential of (61) can be expressed in the and components as

(67)

Now, from (66)

(68)

The Dirac’s delta in (63) implies that

(69)

The above equation permits writing the vector in terms of as

(70)

replacing in (67) one can write the quadratic term as

(71)

where is defined by

(72)

From (66)

(73)

Using (68) and (71) in (52), the option price can be written as

(74)

Integrating over gives

(75)

where must be evaluated from (70) in terms of and as

(76)

where the rectangular matrix is defined by

(77)

It must be noted that, the eigenvalues, and the rectangular matrix are functions of the vector that lies on the null surface. Thus the option price is also a function of. Using (15), (16), (17) and (18) one can write the option price in the space as and is given by

(78)

where the components of the are given by

(79)

and the components of the vector are given in terms of, and according to

(80)

with the components of the rectangular matrix

(81)

When moves over the Kummer surface, the rank of the matrix can change, so the dimensions of and also change, but Equation (78) is always valid.

7. The Propagator Outside S0

When the vector is lying outside the Kummer subsurface, there are regions where the determinant of the correlation matrix is negative. This implies that the propagator given in (58) becomes complex. But, worse than that, in this case one of the eigenvalues is negative, so the propagator given in (57) generates an exponential growth in the associated coordinate. Then the convolution in (52) is not well defined. Thus, one cannot price the option in regions outside the Kummer subsurface that have negative determinant.

8. Conclusions and Further Research

In this research, the existence of the solution of the multi-asset Black-Scholes model has been analyzed in detail. It has been shown that the correlation parameter space, which is equivalent to an N dimensional hypercube, limits the existence of a valid solution for the multi-asset Black-Scholes model. Particularly, it has been demonstrated that inside of this hypercube there is a surface, called the Kummer surface, where the determinant of the correlation matrix is zero, the usual formula for the propagator of the N asset Black-Scholes equation is no longer valid. In particular, the case for three assets and its implied geometry has been studied in detail when the determinant of the correlation matrix is zero. Finally, by using the Wei-Norman theorem, the propagator over the variable rank surface for the general N asset case has been computed, which is applicable over all the Kummer surface, whatever be the rank of the matrix. This formulation corrects the past solution of this problem and its extensions.

As future research, most of the papers related to the multi-asset Black-Scholes model must be revisited in line of our results, as well as others where it is implicitly assumed that a well behaved multivariate Gaussian distribution must exist, as is the case of the stochastic volatility family (see for instance [29] [30] ).

Cite this paper

Contreras, M., Llanquihuén, A. and Villena, M. (2016) On the Solution of the Multi-Asset Black-Scholes Model: Correlations, Eigenvalues and Geometry. Journal of Mathematical Finance, 6, 562-579. http://dx.doi.org/10.4236/jmf.2016.64043

References

  1. 1. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 8, 637-654.
    http://dx.doi.org/10.1086/260062

  2. 2. Merton, R.C. (1973) Theory of Rational Option Pricing. Bell Journal of Economics and Management Science, 4, 141-183.
    http://dx.doi.org/10.2307/3003143

  3. 3. Paul, W. (2000) Paul Wilmott on Quantitative Finance. Wiley, Hoboken.

  4. 4. Jim, G. (2006) The Volatility Surface. Wiley, Hoboken.

  5. 5. Hull, J. and White, A. (1987) The Pricing of Options on Assets with Stochastic Volatilities. The Journal of Finance, 42, 281-300.

  6. 6. Chen, L. (1996) Stochastic Mean and Stochastic Volatility: A Three-Factor Model of the Term Structure of Interest Rates and Its Application to the Pricing of Interest Rate Derivatives. Financial Markets, Institutions, and Instruments, 5, 1-88.

  7. 7. Tomas, B. (2009) Arbitrage Theory in Continuous Time. 3rd Edition, Oxford Finance Series, Oxford.

  8. 8. Margrabe, W. (1978) The Value of an Option to Exchange One Asset for Another. The Journal of Finance, 33, 177-186.
    http://dx.doi.org/10.1111/j.1540-6261.1978.tb03397.x

  9. 9. Stulz, R.M. (1982) Options on the Minimum or the Maximum of Two Risky Assets: Analysis and Applications. Journal of Financial Economics, 10, 161-185.
    http://dx.doi.org/10.1016/0304-405X(82)90011-3

  10. 10. Johnson, H. (1987) Options on the Maximum or the Minimum of Several Asset. Journal of Financial and Quantitative Analysis, 22, 277-283.
    http://dx.doi.org/10.2307/2330963

  11. 11. Reiner, E. (1992) Quanto Mechanics, from Black-Scholes to Black Holes: New Frontiers in Options. RISK Books, London, 147-154.

  12. 12. Shimko, D.C. (1994) Options on Futures Spreads: Hedging, Speculation, and Valuation. Journal of Futures Markets, 14, 183-213.
    http://dx.doi.org/10.1002/fut.3990140206

  13. 13. Embrechts, P., McNeil, A. and Straumann, D. (2002) Correlation and Dependence in Risk Management: Properties and Pitfalls. Risk Management: Value at Risk and Beyond. 1st Edition, Cambridge University Press, Cambridge, 176-223.

  14. 14. Boyer, B.H., Gibson, M.S. and Loretan, M. (1997) Pitfalls in Tests for Changes in Correlations. Board of Governors of the Federal Reserve System, 597. https://www.federalreserve.gov/pubs/ifdp/1997/597/

  15. 15. Patton, A.J. (2004) On the out-of-Sample Importance of Skewness and Asymmetric Dependence for Asset Allocation. Journal of Financial Econometrics, 2, 130-168.
    http://dx.doi.org/10.1093/jjfinec/nbh006

  16. 16. Nielsen, B.F., Skavhaug, O. and Tveito, A. (2008) Penalty Methods for the Numerical Solution of American Multi-Asset Option Problems. Journal of Computational and Applied Mathematics, 222, 3-16.
    http://dx.doi.org/10.1016/j.cam.2007.10.041

  17. 17. Persson, J. and von Sydow, L. (2008) Pricing European Multi-asset Options Using a Space- Time Adaptive FD-Method. Technical Report 2003-059, Department of Information Technology, Uppsala University, Uppsala.

  18. 18. Mehrdoust, F., Fathi, K. and Rahimi, A.A. (2013) Numerical Simulation for Multi-Asset Derivatives Pricing under Black-Scholes Model. Chiang Mai Journal of Science, 40, 725-735.

  19. 19. Kummer, E. (1975) Collected Papers. Vol 2, Springer-Verlag, Berlin.

  20. 20. Hudson, R.W. (1905) Kummer’s Quartic Surface. Cambridge University Press, Cambridge.

  21. 21. Labs, O. (2006) Hypersurfaces with Many Singularities. PhD Thesis, Johannes Gutenberg Universitat, Mainz.

  22. 22. Dolgachev, I.V. (2012) Classical Algebraic Geometry: A Modern View. Cambridge University Press, Cambridge.
    http://dx.doi.org/10.1017/CBO9781139084437

  23. 23. Wei, J. and Norman, E. (1963) Lie Algebraic Solution of Linear Differential Equations. Journal of Mathematical Physics, 4, 575-581.
    http://dx.doi.org/10.1063/1.1703993

  24. 24. Lo, C.F. and Hui, C.H. (2002) Pricing Multi-Asset Financial Derivatives with Time-Dependent Parameters-Lie Algebraic Approach. International Journal of Mathematics and Mathematical Sciences, 32, 401-410.
    http://dx.doi.org/10.1155/S016117120211101X

  25. 25. Martin, J.F.P. (1968) On the Exponential Representation of Solutions of Linear Differential Equations. Journal of Differential Equations, 4, 257-279.
    http://dx.doi.org/10.1016/0022-0396(68)90038-7

  26. 26. Charzyński, S. and Kus, M. (2013) Wei-Norman Equations for a Unitary Evolution. Journal of Physics A: Mathematical and Theoretical, 4, Article ID: 265208.
    http://dx.doi.org/10.1088/1751-8113/46/26/265208

  27. 27. Kleinert, H. (2006) Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets. 4th Edition, World Scientific, Singapore.
    http://dx.doi.org/10.1142/6223

  28. 28. Chaichian, M. and Demichev, A. (2001) Path Integrals in Physics. Vol. 1, IOP Publishing, Bristol.

  29. 29. Contreras, M. (2015) Stochastic Volatility Models at as a Second Class Constrained Hamiltonian Systems. Physica A, 405, 289-302.
    http://dx.doi.org/10.1016/j.physa.2014.03.030

  30. 30. Contreras, M. and Hojman, S. (2014) Option Pricing, Stochastic Volatility, Singular Dynamics and Path Integrals. Physica A, 393, 391-403.
    http://dx.doi.org/10.1016/j.physa.2013.08.057

Journal Menu>>