Received 11 May 2016; accepted 28 August 2016; published 31 August 2016

ABSTRACT

In this paper, some basic results of stochastic calculus are revised using the following observation: For any semimartingale, the series of jumps at predictable stopping times converges a.s. on any finite time interval, whereas the series of jumps at totally inaccessible stopping times diverges. This implies that when studying random measures generated by jumps of a given semimartingale, it is naturally to define separately a random measure 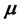generated by the jumps at totally inac- cessible stopping times and an other random measure generated by the jumps at predictable stopping times. Stochastic integrals 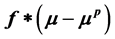are well defined for suitable functions f, where 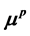is the predictable compensator of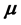. Concerning the stochastic integral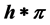, it is well defined without any compensating of the integer valued measure.

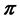Keywords:

Random Measures, Semimartingales, Stochastic Integrals, Predictable Stopping Times

1. Introduction

Stochastic calculus deals with stochastic integrals and stochastic processes constructed by making use of these integrals.

Initially the stochastic integrals were defined with respect to the Wiener process and the Poisson measures by K. Ito (see [1] ). An important contribution in the theory of stochastic processes based on stochastic integrals belongs to A. V. Skorokhod [2] (see also I. I. Gihman and A. V. Skorokhod [3] ).

The Poisson measures are generated by jumps of stochastically continuous independent increments processes (IIP’s). Note that up to subtract a deterministic function, any IIP is a semimartingale. These processes may admit a countable number of small jumps on any finite time interval. For any such process X, the series of jumps

(1)

diverges a.s. for any, where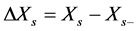. This kind of series converges only in the case when the jumps are bounded from zero, i.e.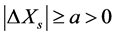. As consequence, if 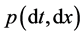is the Poisson measure generated by X:

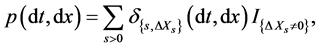(2)

where 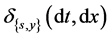is the Dirac measure at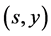, then the stochastic integral

(3)

does not exist in general case, where E is the state space of X (in particular, for, this integral equals the above series of jumps). For this reason, one must use the compensated Poisson measure with

(4)

Then the stochastic integral

(5)

is well defined, for a suitable predictable function. This process possesses the properties:

(6)

(7)

(8)

when the stochastic integral exists.

Multiple applications of the stochastic calculus have needed an extension of random measures and stochastic integrals, in particular, to consider the integer-valued measures generated by semimartingales.

A general class of random measures suitable for construction of stochastic integrals was studied by J. Jacod [4] , R. Liptser and A. Shiryaev [5] (see also Jacod J. and Shiryaev A. [6] ). Without loss of generality, we con- sider random measures generated by jumps of càdlàg semimartingales.

Let be an integer-valued measure generated by jumps of a semimartingale X, i.e.

(9)

Similarly to case of the Poisson measure, the stochastic integral of kind does not exist (except a particular case). For this reason, in [5] [7] for a suitable functions h, a stochastic integral is defined, where is a predictable compensator of the measure. The properties of this integral are different of those of the above integral with respect to the Poisson measure. In particular,

(10)

We propose an alternative approach defining stochastic integrals with respect to random measures generated by jumps of semimartingales.

For any semimartingale X, there exist sequences

of totally inaccessible and predictable, respectively, stopping times (s.t.’s) which absorb all jumps of X. The graphs of all and are disjoint (see [1] ).

The important property of jumps of X at predictable s.t.’s is that, for any, the series

(11)

converges a.s. (in contrast with the series which diverges).

This result implies that one can define a stochastic integral with respect to the integer-valued measure generated by the jumps at predictable s.t.’s without making use of the predictable compensator.

In the paper we consider the integer-valued measures and generated by jumps of a semimartingale X at totally inaccessible and predictable, respectively, s.t.’s, and define stochastic integrals and. Note that the second integral is a local martingale or a semimartingale according to properties of the function h. For this second integral, we give necessary and sufficient conditions on the function h for which the process is a semimartingale. Such result was not considered earlier.

Concerning the our integral with respect to the measure it is the same as in [4] [5] if the measure there has been generated only by the jumps at totally inaccessible s.t.’s, that is the process generating the measure has not the jumps at predictable s.t.’s.

It should be clarified the difference in results of applying the construction of stochastic integrals with respect to the measure given in [4] [5] and that proposed in this paper for the measure. It turns out that the

first construction leads to addition and subtraction of the term as, for

example, in the exponential semimartingale (see (29) and Proposition 4). In some other applications the first construction leads to addition and subtraction of the integral with respect to the compensator, , as in the Ito formula. In our construction such a kind of addition and subtraction of some terms is not used.

As application, we revise some basic results of stochastic calculus by making use of this construction of stochastic integrals.

One of consequences of this approach is the following innovation representation of any semimartingale (see Theorem 11 and the formula (71)):

(12)

where are continuous processes, v is of finite variation, m is a local martingale, is an integer valued measure with continuous compensator. Note that the innovation representation is important in statistics of random processes. It was used in nonlinear filtering of diffusion processes (see R. Liptser and A. Shiryaev [8] ). The representation is similar to that of IIP’s.

This representation implies that any semimartingale X can be presented as where

, and is a quasi left continuous semimartingale,.

The paper is organized as follows.

In Section 2, we give some necessary general notions. In Section 3, the convergence of series of semi- martingale jumps at predictable s.t.’s is proved and some direct applications are discussed. Section 4 contains the construction of stochastic integrals with respect to the measures and generated by a semi- martingale X. Sections 5-6 contain the innovation presentation of semimartingales and the Ito formula, respectively, revised by using the given construction of stochastic integrals.

2. Some General Notions

Let be a filtered probability space with -completed right-continuous filtration.

We denote (resp.) the optional (resp. the predictable) s-field on the product-space. Remind that is generated by the F-adapted right continuous processes having left-side limits (càdlàg ); is generated by the F-adapted continuous processes.

Denote E the state space (usually or) and (resp.) the s-field on the pro- duct-space:

(13)

Let X be a semimartingale,. We denote the continuous martingale component of X and [X,X] the optional quadratic variation:

(14)

2.1. Optional and Predictable Projections

Let X be a bounded or positive F-adapted process. There exists an -measurable process (resp. -measurable process) such that

(15)

a.s. for any s.t. T (resp.

(16)

a.s. for any predictable s.t. S).

The process (resp.) is called the optional (resp. the predictable) projection of X on the optional (resp. predictable) s-field. Each of these projections is unique to within modification on a P-null set (see [9] ).

2.2. Random Measures

We begin this subsection with some notions and results about random measures (see the book by J. Jacod [4] for details).

Let be the Lusin space with the borelian s-algebra (really, we use the case when). A random measure is a family of s-finite measures on.

A random measure is called to be integer-valued if

1)

2)

The measure is optional (resp. predictable) if the process is optional (resp. predictable) for any function (resp.).

2.3. Dual Predictable Projection of a Random Measure

Now we give a basic result on existence of a dual predictable projection (a predictable compensator) of a random measure.

Theorem 1. Let be a random measure for which there exists -predictable partition of such that, for any n. Then there exists a unique predictable measure (called a pre- dictable compensator of) verifying the property:

1) (17)

for with for any n.

2) If -measurable function W is such that the process is of locally integrable variation, , then the property 1) is equivalent to the following one:

(18)

where is the dual predictable projection of the process.

If is an integer-valued measure generated by a semimartingale X, then for any predictable s.t. S,

(19)

3. Convergence of Series of Semimartingale Jumps at Predictable s.t.’s

Let be a semimartingale,

(20)

where m is a local martingale, , A is a process of finite variation on any finite interval a.s., ,

i.e. a.s. for any.

There exist the sequences

(21)

of totally inaccessible and predictable stopping times (s.t.’s), respectively, which absorb all jumps of X. The graphs of all and are disjoint.

From finiteness of the optional quadratic variation it follows that, for any,

(22)

For the jumps at the predictable s.t.’s we get the following stronger result.

Theorem 2. Let be a semimartingale from (20) and be the sequence of predictable s.t.’s from (21). Then the series

(23)

converges a.s. for any, and the process is a semimartigale,.

Proof. We consider some particular cases (see [7] ). For any,.

1) The series converges absolutely a.s.. Hence the process is of finite

variation on any finite interval.

2) Let m belongs to. Even if it means localizing we suppose with. This norm is equivalent to. We set. Then, for,

(24)

when, where the second equality follows from orthogonality of martingales

(25)

and convergence to 0 follows from integrability of optional quadratic variation,. Hence converges in. Choosing a subsequence of indexes n we obtain that this series converges a.s. Hence the process is a martingale from.

This two cases imply that the process is a semimartingale.

3) Let m be from. Due to the Davis decomposition, there exists a sequence of s.t.’s such that a.s. and , for any k, one has, where (see [10] ). The pre- vious particular cases provide, for any k,

(26)

Since a.s., we obtain the statement of theorem. ,

3.1. Applications of Theorem 2

We shall give two applications of this result.

Proposition 3. Let X be a semimartingale from (20) and be the sequence of predictable s.t.’s from (21). Then X admits a decomposition

(27)

where is a quasi left continuous semimartingale,

(28)

The decomposition is unique to within modification on a -null set.

Proof. The semimartingale absorbs all jumps of X at predictable s.t.’s. Hence the process is a quasi left continuous semimartingale. ,

The exponential semimartingale. Let X be a semimartingale. It is well-known the exponential semi-martingale (called the Dolean exponential)

(29)

where the infinite product converges a.s. for any and it is the process of finite variation. The semi- martingale Z is a unique solution of the equation

(30)

The following result gives an other form of the solution of Equation (30) taking into account the Theorem 2.

Proposition 4. Let X be a semimartingale from (20) and be the sequences of predictable and totally inaccessible, respectively, s.t.’s from (21). Then the exponential semimartingale

(31)

is the solution of the Equation (30), where, the product con- verges a.s. for any and it is a semimartingale, the product is the process of

finite variation for any.

In particular, if the semimartingale X has the jumps only at predictable s.t.’s:

(32)

then the exponential semimartingale is as follows:

(33)

Proof. Due to Theorem 2 and Proposition 3, the Dolean exponential (29) can be presented as in (31).

One has to show only that the product converges a.s. and it is a semimartingale. To that

end, note that there is a finite number of jumps such that. Hence the process with

(34)

is of finite variation for any.

Denote

(35)

For the process one has

(36)

where. The first series on the right-hand size converges a.s. and it is a semimartingale, due to Theorem 2, and the second one converges absolutely and it is a process of finite variation being bounded by the series

(37)

Therefore, the process is a semimartingale and by the Ito formula (see Lemma 2), the processes

is a semimartingale as well. The equality yields the result. ,

Remark 1. It should be noted that in the exponential (29) the term is presented two

times: the first time in the first exponential, since, and the second time it is in the infinite product as. By dropping these two terms we come to (31).

4. Stochastic Integrals with Respect to the Random Measures m − m^p and p

Let X be a semimartingale with values in E.

On the product space, we define two integer-valued random measures

(38)

where is the Dirac measure, is the indicator of the set.

Let us set

(39)

We denote by (resp.) the predictable compensator of (resp., of). Since X has not a jump at the time,

(40)

Proposition 5. The measure is continuous, i.e. the process is continuous for any.

Proof For any predictable s.t. S and any, one has since. This

implies. From here it follows that a.s., since. This

means that the process has not jumps at any predictable stopping time. ,

Proposition 6. The set is sparse. Moreover

(41)

Proof. The definition of implies. Hence J is sparse.

Let S be a predictable s.t. such that. Then a.s. That is

if, then. This implies. Reciprocally, let S be a predictable s.t. such that

. Then a.s.. This implies a.s. and this means that J is a predictable support of. Note that means, where is the projection of the set onto. ,

Our aim is to define stochastic integrals of following kinds:

where denotes the space of purely discontinuous local martingales.

In order to define a stochastic integral which is a purely discontinuous local martingale, the following result is the basic one.

Lemma 1. Let Y be an optional process. For existence a unique process possessing the property it is necessary and sufficiently that

1),

2).

For the proof of this result (see J. Jacod [4] , Theorem 2.45).

4.1. Stochastic Integrals with Respect to the Random Measures m − m^p.

Let us introduce the functional spaces, for,

(42)

where (resp.) denote the space of processes of integrable (resp. locally integrable) variation.

By making use of Lemma 1, we obtain the following results about stochastic integrals with respect to the random measure. This integral is the same that is given in [4] [5] , when the predictable compensator is continuous (see Proposition 5).

Theorem 7. Let f be -measurable function. For existence a unique process possessing the property

(43)

it is necessary and sufficiently that.

The process Z is called to be the stochastic integral.

Proof. Sufficiency: Since, one has to prove that the predictable projection

Taking into account that, for any predictable stopping time S and any totally inaccessible stopping time T, , we obtain

(44)

(45)

Due to Lemma 1, this condition and that of provide existence of unique which is called the stochastic integral.

Necessity: It follows from Lemma 1. ,

Remark 2. We have for optional quadratic variation of:

(46)

Remark 3. If, then is a square integrable martingale, , and

(47)

The condition is an optional integrability condition with respect to the measure. The next result gives predictable integrability conditions.

Proposition 8. Let f be -measurable function and. The following conditions are equivalent:

1)

2)

3

4)

Proof. Due to Theorem 1, for any -measurable function W,

(48)

1)Û2): Denote. It is easy to see the following equivalences

(49)

where is the space of the optional processes of locally finite variation.

1) Þ 2): Even if it means localizing, we suppose. This implies by (49). The sequence of s.t.’s increases a.s. to and

(50)

since due to the inequality. being integrable, one has.

This and (48) imply (ii).

1) Ü 2): Even if it means localizing, we suppose. This implies by (49). The sequence of s.t.’s increases a.s. to. Since, one has

(51)

This implies, hence 1).

The equivalences 2Û 3), 2)Û 4) follow from the inequalities:

(52)

and if,

(53)

4.2. Stochastic Integrals with Respect to the Random Measure p

Now we consider stochastic integrals with respect to the measure p which is a purely discontinuous local martingale.

Theorem 9. Let h be -measurable function. Denote, for,

(54)

where

(55)

For existence a unique process possessing the property

(56)

it is necessary and sufficiently that.

The process Z is called to be the stochastic integral.

Proof. We have to verify only the condition. One has

(57)

Due to Theorem 1,. This implies. Now the result follows from Lemma 1. Note that

(58)

since.

Remark 4. In the defined stochastic integral, the random measure is not a martingale measure. One can define a stochastic integral of predictable function h with respect to a martingale measure. Indeed, due to Lemma 1 for existence a unique process possessing

the property, it is necessary and sufficiently that.

The process Z is called to be the stochastic integral (see [4] [5] ). Since the jumps are the same, , we have two different forms of the same process and.

Remark 5. For the optional quadratic variation of one gets:

(59)

If, then one has for the predictable quadratic variation

(60)

4.3. Semimartingale Stochastic Integrals

We have studied stochastic integrals which are local martingales. Now we consider a stochastic integral with respect to the integer-valued measure p that is a semimartingale.

Denote by the space of semimartingales that are purely discontinuous with jumps at predictable s.t.’s and by the sub-set of special semimartingales,.

We denote the space of -measurable functions h:

(61)

Theorem 10. Let be -predictable function. For existence a unique semimartingale with the jumps at predictable s.t.’s

(62)

it is necessary and sufficiently that and.

The semimartingale Z is denoted.

Proof (Þ): Let with jumps

(63)

at predictable s.t.’s S. Since Z is a special semimartingale, , where. One has. From here, since and A is predictable, we get

(64)

Therefore, and.

Further, , since where

, is the complement of J. Therefore, as, one has

(65)

(Ü): Conditions of theorem implies existence of martingale with jumps at pre- dictable s.t.s. The process

(66)

Corollary 1. Let be -predictable function. For existence a unique semimartingale with the jumps at predictable s.t.’s

(67)

it is necessary and sufficiently that and, for some.

The semimartingale Z is denoted.

5. Innovation Presentation of Semimartingales

Let, i.e.

(68)

where. Denote the filtration generated by the semi-

martingale X,. By we denote the filtration obtained from by making right-hand continuity and completeness.

Let (resp.) be the optional (resp. predictable) s-field on related to the filtration. Note that in (68), the right-hand terms A and M are not -measurable in contrast with the left-hand process X. We shall give the so-called innovation presentation of X that provides the decomposition of X in the sum of -measurable components. This presentation is important, for example, in statistics, when every estimator based on X should be presented in terms of -measurable components of X.

We begin with sequences and of predictable and totally inaccessible, respectively, - stopping times which absorb all discontinuity times of X. Define two random integer-valued measures and on:

(69)

(70)

Denote by the -predictable compensator of the measure.

The next result clarifies the -structure of X.

Theorem 11. Let be a semimartingale. Then

(71)

where

(72)

(73)

(74)

where are continuous processes,.

Proof. From the definition of the measure, one has, for any,

(75)

and due to Theorem 1, the stochastic integral in the right-hand side is a -measurable semimartigale,.

Denote

(76)

The process is a -measurable semimartigale being the sum of a -local martingale and a -measurable process of locally finite variation. absorbs all jumps of X at times. Indeed

(77)

Then the process

(78)

is an -special continuous semimartingale. Therefore, v is continuous and belongs to. Taking the -duel predictable projection we obtain

(79)

Remark 6. Taking into account that the last term in (71) has the form

(80)

one can say that the structure of càdlàg semimartigales is similar to that of càdlàg processes with independent increments.

Indeed, up to subtraction a deterministic function, any càdlàg process with independent increments Y can be presented as follows

(81)

where is a deterministic continuous process of finite variation, is a continuous local gaussian martingale, is a Poisson measure, and is a sequence of deterministic s.t.’s (see [11] [12] ).

Remark 7. It is known that the semimartigale property is stable with respect to a narrowed filtration (see, for example, [4] ). In our case, the result claims that any -measurable process from belongs also to.

6. The Ito Formula

Lemma 2. Let be a twice continuously differentiable function and Y be a semimartingale,

(82)

where are the components in the innovation presentation (71) of a semi-

martingale X; are predictable functions, a.s. for any;

. Then the process is a semimartingale and, for any,

(83)

where.

Proof. The Ito formula is well known when the semimartingale (82) has not the last term.

We explain only that the last term in (83) is well defined and it is a semimartingale. Denote

and. Let. One has

(84)

where

(85)

For we have to verify the conditions of corollary of theorem 10. One has

(86)

(87)

Taking into account that a.s. and the property yield.

Let us show that. One has

(88)

since a.s., and

(89)

since the process has a finite number of jumps in absolute value greater than 1 on any finite time interval. As, one obtains. ,

7. Conclusion

We have proposed an alternative approach to constructing stochastic integrals with respect to random measures generated by the jumps of semimartingales. We consider two random measures, (resp.) is generated by the jumps at totally inaccessible (resp. predictable) s.t.’s, and we define stochastic integrals and. The first stochastic integral possesses the properties similar to that of integral with respect to the Poisson measure. The integral can be a local martingale or semimartingale following the properties of the function h. The last integral is a series of random variables, since the measure and the compensator are discrete on the time space. These properties of stochastic integrals make more clear the structure of semi-martingales and make easier their applications to discontinuous phenomena, in particular, to financial problems.

Acknowledgements

The author thanks the referee for valuable comments and suggestions, and the Editor for kind invitation to this Special Issue.

Cite this paper

Leonid Galtchouk, (2016) About Stochastic Calculus in Presence of Jumps at Predictable Stopping Times. Journal of Mathematical Finance,06,443-456. doi: 10.4236/jmf.2016.63035

References