Journal of Mathematical Finance
Vol.05 No.01(2015), Article ID:54224,8 pages
10.4236/jmf.2015.51007
A Real Options Approach to Distressed Property Borrower-Lender Reconciliation
David J. Moore*, Nuriddin Ikromov
College of Business Administration, California State University, Sacramento, CA, USA
Email: *djmphd@csus.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 February 2015; accepted 23 February 2015; published 25 February 2015
ABSTRACT
We propose a real option framework to value distressed properties and restructure their loans. Our approach reconciles the interests of borrowers and lenders through a constrained optimization model yielding mutually beneficial restructure terms. Borrowers receive lower loan balances and payments, while lenders replace non-performing loans with performing loans that have higher market values. A numerical illustration shows that the market value of a restructured loan can exceed that of the original non-performing loan and the post-foreclosure cash flows when the lender repossesses the property.
Keywords:
Real Option, Real Estate, Restructure, Distressed Property, Market Value

1. Introduction
Many studies have applied option theory to real estate investment, abandonment, and timing decisions over the past three decades. [1] is one of the first studies to applying real options theory to real estate development and to offer a theoretical model of valuation of vacant lots. [2] offers an analytical and numerical solution for the option to develop or abandon real estate. [3] - [5] derive models of pricing lease contracts in the option pricing context. [6] applies real option theory to value adjustable-rate mortgages in the presence of default, and [7] surveys the theoretical studies on the option pricing methodology of mortgage valuation. [8] applies option theory to explain the cyclical nature of real estate markets. [9] finds that individual investors are unable to apply real options theory to investment decisions in a laboratory experiment. However, prior real estate applications of option theory are from the perspective of developers or financial institutions. To our knowledge, this study is the first to apply option theory to real estate from a household perspective. This study extracts home values from the option pricing framework. We then use the estimated market value in a constrained maximization problem to produce mutually beneficial loan restructure terms.
Figure 1 illustrates that the market-to-book ratio for non-performing loans is consistently lower than that of performing loans from 1990 to 2013. Overall, the average market-to-book value of non-performing loans (35%) is less than half of performing loans (83%). We investigate whether or not a non-performing loan can be restruc- tured into a performing loan, if the restructured loan (likely with a lower balance) has a higher market value than the original non-performing loan, and if the new loan terms are in the best interest of the borrower and lender.
The precipitous drop in home loan market values coupled with increased reserve requirements has necessitated loan restructuring. However lenders are often unwilling to restructure loans. We suggest one reason lenders are apprehensive is that they are unaware of the related issues of current home valuation and optimum restructuring terms. [10] refers to this scenario as “a lender’s dilemma.” Our study proposes a constrained optimization model that provides optimal loan restructuring terms and distressed property valuation. We obtain these results by observing that borrowers have a real option and incorporating the value of that option in the lender’s maximization problem.
To illustrate the potential benefits to borrowers and lenders, consider the average market-to-book values for performing and non-performing loans, 83% and 35%, respectively. The restructured loan market value will exceed the non-performing loan market value as long as the restructured principal balance is greater than
 of the original principal balance. For example, assume anon-performing loan balance of $100,000. Further assume that a reduction of principal balance to $70,000 produces a performing loan. The market values before and after restructuring are:
of the original principal balance. For example, assume anon-performing loan balance of $100,000. Further assume that a reduction of principal balance to $70,000 produces a performing loan. The market values before and after restructuring are:
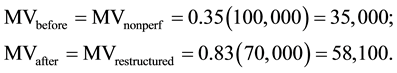
The lender can increase the market value of the non-performing loans 66% by restructuring into performing loans. Of course there are many other choice variables for the lender such as the loan rate and term. The trio of principal reduction percentage, loan rate, and loan term are used as the lender’s choice variables in our model that follows.
2. Model
For the purposes of this study, a “distressed” property is a property where a homeowner has ceased repayment due an “underwater” condition: the current loan balance exceeds the current market value of the home. Our
Figure 1. Average market-to-book ratio for performing and nonperforming loans from 1990 to 2013. Source: FDIC historical loan sales data (http://www.fdic.gov/buying/historical/index.html).
model first implementsthe underwater condition by setting the real option value to the borrower to zero, and then solving for the current market value of the home S0 (“stock price” in standard options nomenclature). Given the current distressed property market value S0 and existing loan amount K0, the lender chooses the principal reduction amount a, new interest rate r, and new loan term T that maximizes the value of the now-performing loan
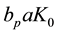 subject to several constraints. The constraints are defined to ensure the real option to the home- owner is positive (the performing condition), the market value of the restructured performing loan exceeds that of the existing non-performing loan, and the loan terms are within reasonable market conditions. We begin by describing the assumptions and constraints in detail then follow with the model specification.
subject to several constraints. The constraints are defined to ensure the real option to the home- owner is positive (the performing condition), the market value of the restructured performing loan exceeds that of the existing non-performing loan, and the loan terms are within reasonable market conditions. We begin by describing the assumptions and constraints in detail then follow with the model specification.
2.1. Assumptions
We make several simplifying assumptions for model tractability. These assumptions are intentionally restrictive in that we do not intend for this model to apply to all non-performing loans. However, loans that meet the criteria identified in the following assumptions do represent a subset of all non-performing loans.
Assumption 1: The non-performing loan represents a negative equity scenario where the real option value on the home is equal to zero. Admittedly, it is possible that a loan is non-performing for reasons other than negative equity. The borrower may have experienced unemployment or under-employment recently or an investor may walk away from a property in which mortgage payments exceed rental income. In either case, borrowers and investors can avoid default by selling unless the home has negative equity. Hence, this study focuses on negative equity distressed properties.
Assumption 2: The loan will become performing after restructuring. The restructured loan, by construction of our model, has a lower balance, lower monthly payments, and a positive real option value. Assuredly, not all home loans can be restructured. However, we consider successful convergence to a solution, subject to several constraints, an indication of potential applicability. We deem the loan a restructure candidate when the model converges to a solution. We do not consider the loan a restructure candidate when the model does not converge.
Assumption 3: The home price process follows a lognormal distribution. We make this assumption to apply the Black-Scholes pricing valuation to our model. This is a standard assumption with option pricing made in [11] , and implemented in [12] and [13] .
Assumption 4: The The borrower’s time horizon is t years. We acknowledge that the same agreement was made in the non-performing original loan. However, since the output of our model is a restructured loan beneficial to both the borrower and the lender, we consider t, which is distinct from the loan term T, a required commitment from the borrower for restructuring to occur.
Additional simplifying assumptions.We further assume the market-to-book-value of non-performing loans and performing loans remains constant. In line with option pricing practice, we also assume that price volatility and the risk free rate are stationary, there are no transaction costs or taxes, and the stock (home) does not pay a dividend. It is true that these assumptions do not always hold in the real world. However, the transaction costs and taxes will be minimal for a distressed property due to a major decline in value. In addition, although rental revenue may be positive, it is likely offset by costs of maintaining the property. Finally, [1] describes, if real estate investments of publicly-traded firms “are chosen in a manner consistent with value maximization, then real estate prices will be determined in equilibrium as if markets were really frictionless.”
2.2. Current Home Value Based on Real Option Value under Distress
The current valueof the distressed property
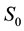 is obtained by setting value of the distressed home real option
is obtained by setting value of the distressed home real option
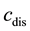 equal to zero:
equal to zero:
 (1)
(1)
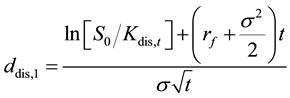 (2)
(2)
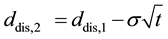 (3)
(3)
where
 is future value of the distressed loan if the borrower continued making payments.
is future value of the distressed loan if the borrower continued making payments.
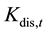 is computed as
is computed as
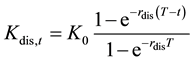 (4)
(4)
where
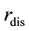 is the current interest rate on the distressed loan. We use numerical methods to solve Equation (1) for
is the current interest rate on the distressed loan. We use numerical methods to solve Equation (1) for .
.
2.3. Real Option Value under Restructuring
The real option value of the restructured loan to the borrower is computed in the same fashion as under distress with changes to the interest rate
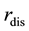 and strike price
and strike price
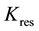 using the Black-Scholes option pricing model:
using the Black-Scholes option pricing model:



where





2.4. Real Option Value under Foreclosure
Should the lender reposses the home and sell on the open market (referred to Real Estate Owned or REO sale), the foreclosed home will sell at a discount to its current market value. This discount can be attributed to ex- pected repairs associated with a property that has been vacant for six months or more (RealtyTrac). In a REO sale both the lender and third party buyer incur repair expenses [14] . Let









where

Note that the cash flow to the lender in the REO sale is not the sale price

2.5. Constrained Optimization Model
The lender chooses the loan balance discount a, the new loan interest rate


where
















Constraint C1: The restructured loan must be smaller than the original loan. This constraint follows Assump- tion 1 and the suggestion by [15] to reduce loan balances and split potential gains (Constraint C2) to fix the US mortgage crisis. In addition, this constraint focuses our model on negative equity non-performing loans and en- sures a lower monthly payment. The combination of lower loan balance and lower monthly payments follows Assumption 2: the loan will become performing after restructuring.
Constraint C2: The borrower and lender evenly split potential gains. This constraint guides our model to a solution that is mutually beneficial to borrowers and lenders. Simply reducing a principal balance just to bring a borrower current may be insufficient incentive for a lender. We incorporate the suggestion of shared gains [15] via this constraint.
Constraint C3: The market value of the restructured performing loan must exceed the market value of the current non-performing loan. This constraint is included to ensure that restructuring is beneficial to the lender. Without this constraint it would be possible to restructure into a performing loan whose market value is lower than the current non-performing loan.
Constraint C4: The new loan rate must be greater than or equal to the market rate for performing loans.A lender may be unable to fund loans at rates below the current market rate. Therefore, we require the restructured rate tobe at least the average market rate for performing 30 year loans.
Constraint C5: The new loan term is between the current loan term and 30 years. Given the finite lives of borrowers and customary industry practice we restrict the maximum new loan term to 30 years. Also, setting the minimum term to the remaining term on the existing loan follows Assumption 2 (the loan will become perform- ing due to lower balance and payment).
Again, we utilize numerical optimization methods to solve the constrained optimization problem in Equation (13) to produce optimum values of the lender choice variables
3. Numerical Illustration
3.1. Data and Parameterization
We obtain the average market rate for 30 year conforming loans










Table 1 summarizes the exogenous variables, values, and sources used in this study. Figure 2 depicts the FHFA US home price index level data. The rapid growth in housing prices from 1997 to the 2006 peak, the
Table 1. Parameters, values, and sources.
Figure 2. US housing price index level from 1991Q1 to 2014Q3. Source: Federal Housing Finance Agency.
correction from 2006 to mid-2011, and the post-2011 rebound are evident. Figure 3 depicts the returns calculated from the FHFA US home price index level data. Returns averaged 3.36% with a standard deviation of

3.2. Distressed Property Valuation
We begin our illustration with the median values of negative equity loans from [16] . Specifically, we establish our base case by setting the currently non-performing loan balance to the median mortgage balance at termination (default)



Next, we perform a sensitivity analysis to investigate factors that impact distressed property values. The results of the sensitivity analysis are presented in Figure 4. Several observations are of note. First, home valuesare most sensitive to the current non-performing loan balance

Figure 3. US housing price index returns from 1991Q1 to 2014Q3. Source: Federal Housing Finance Agency.
Figure 4. Home value sensitivity to changes in model inputs.
lower value. This could reveal that additional years of payments were unable to bring the loan balance of an extremely inflatedpurchase price in line with the fundamental value. Third, home values are relatively insensitive to the original interest rate
3.3. Borrower-Lender Reconciliation
We determine optimum loan restructuring terms for the base case using our real options-based distressed property value estimate. We employ numerical methods [17] to solve the constrained nonlinear optimization model of Equation (13). The optimized loan reduction amount, loan rate, and loan term are




to the lender post foreclosure sale
We now examine optimality conditions for different non-performing loan balances. Table 2 details the impact of initial loan balance







3.4. Analysis of Results
The restructured value



4. Conclusion
We present a method to establish the market value of distressed properties and a model to reconcile the interests
Figure 5. Value to lender under base case.
Table 2. Model outputs.
of borrowers and lenders. Our approach applies real option theory using the Black-Scholes option pricing formula, a constrained maximization framework, and numerical methods. Sensitivity analysis reveals distressed property values are most sensitive to the non-performing loan balance and least sensitive to market volatility. The non-performing loan balance sensitivity indicates information remains in the non-performing balance. The volatility insensitivity suggests the resulting negative equity position of distressed homes is driven more by inflated purchase prices than overall market volatility. We present evidence that restructuring is the highest value alternative among the lender’s choice to sell the loan, foreclose, or restructure. Borrowers also benefit from prin- cipal and interest rate reductions. We show that the real option under restructuring is a significant improvement over the zero-value option during non-performance. Overall, we believe our approach can be used to arrive at mutually beneficial loan terms thereby relieving current and future negative equity positions.
Cite this paper
David J.Moore,NuriddinIkromov, (2015) A Real Options Approach to Distressed Property Borrower-Lender Reconciliation. Journal of Mathematical Finance,05,73-81. doi: 10.4236/jmf.2015.51007
References
- 1. Titman, S. (1985) Urban Land Prices under Uncertainty. The American Economic Review, 75, 505-514.
- 2. Williams, J.T. (1991) Real Estate Development as an Option. The Journal of Real Estate Finance and Economics, 4, 191-208.
http://dx.doi.org/10.1007/BF00173124 - 3. McConnell, J.J. and Schallheim, J.S. (1983) Valuation of Asset Leasing Contracts. Journal of Financial Economics, 12, 237-261.
http://dx.doi.org/10.1016/0304-405X(83)90037-5 - 4. Grenadier, S.R. (1995) Valuing Lease Contracts a Real-Options Approach. Journal of Financial Economics, 38, 297-331.
http://dx.doi.org/10.1016/0304-405X(83)90037-5 - 5. Grenadier, S.R. (1996) Leasing and Credit Risk. Journal of Financial Economics, 42, 333-364.
http://dx.doi.org/10.1016/0304-405X(83)90037-5 - 6. Kau, J.B., Keenan, D.C., Muller III, W.J. and Epperson, J.F. (1993) Option Theory and Floating-Rate Securities with a Comparison of Adjustable-and Fixed-Rate Mortgages. Journal of Business, 66, 595-618.
http://dx.doi.org/10.1086/296619 - 7. Kau, J.B. and Keenan, D.C. (1995) An Overview of the Option-Theoretic Pricing of Mortgages. Journal of Housing Research, 6, 217-244.
- 8. Grenadier, S.R. (1995a) The Persistence of Real Estate Cycles. The Journal of Real Estate Finance and Economics, 10, 95-119.
http://dx.doi.org/10.1007/BF01096984 - 9. Yavas, A. and Sirmans, C.F. (2005) Real Options: Experimental Evidence. The Journal of Real Estate Finance and Economics, 31, 27-52.
http://dx.doi.org/10.1007/s11146-005-0992-6 - 10. Berger, J.A., Sullivan, M.P. and Sood, S.S. (2009) Restructuring Non-Performing Commercial Real Estate Loans: A Lender’s Dilemma. Real Estate Finance Journal, 25, 5.
- 11. Hull, J.C. (2006) Options, Futures, and Other Derivatives. Sixth Edition, Prentice-Hall, Englewood Cliff.
- 12. Benninga, S. and Wiener, Z. (1997) The Binomial Option Pricing Model. Mathematica in Education and Research, 6, 27-34.
- 13. Benninga, S. and Wiener, Z. (1997) Binomial Option Pricing, the Black-Scholes Option Pricing Formula, and Exotic Options. Mathematica in Education and research, 6, 11-14.
- 14. La Jeunesse, E. (2013) Home Improvement Spending on Distressed Properties: 2011 Estimates. Joint Center for Housing Studies, Harvard University, N13-1.
- 15. Wheaton, W. (2010) A Fair and Easy Way to Fix the US Mortgage Crisis. Business Insider.
http://www.businessinsider.com/a-fair-and-easy-way-to-fix-the-us-mortgage-crisis-2010-9 - 16. Bhutta, N., Dokko, J. and Shan, H. (2010) The Depth of Negative Equity and Mortgage Default Decisions. Division of Research & Statistics and Monetary Affairs, Federal Reserve Board.
- 17. Powell, M.J. (1994) A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. In: Gomez, S. and Hennart, J.-P., Eds., Advances in Optimization and Numerical Analysis: Mathematics and Its Applications, Springer Netherlands, 51-67.
http://dx.doi.org/10.1007/978-94-015-8330-5_4
NOTES
*Corresponding author.








