Journal of Mathematical Finance
Vol.03 No.04(2013), Article ID:38962,6 pages
10.4236/jmf.2013.34047
Investor Naïveté and Asset Prices
Economic Research Service, US Department of Agriculture, Washington DC, USA
Email: jacook@uci.edu
Received September 17, 2013; revised October 18, 2013; accepted October 30, 2013
Copyright © 2013 Jonathan Cook. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
This paper describes strategic behavior in a nonequilibrium model of asset pricing with heterogeneous sophistication. Both risk and return are increasing in the naïveté of investors in the market. Optimal investment involves considering the effect that naïve investors have on the market. Further, we derive a simple characterization of the asset price dynamics that results from an arbitrary combination of a countably infinite set of investor types.
Keywords: Level-k Model; Nonequilibrium Strategic Thinking; Technical Analysis
1. Introduction
A large literature in finance has questioned the efficient market hypothesis. The failure of markets to be efficient is often attributed to naïve behavior by some investors. Naïve behavior by investors creates opportunities for more sophisticated investors who are able to exploit the mispricing created by naïve investors.
This is the first paper to explore the role of k-level thinking in an asset pricing model. Level-k theory provides a tool for analyzing games in which players differ in their sophistication. Work in experimental economics [1-4] has shown that models in which players differ in the number of cognitive steps that they take illuminate behavior in games that require predicting the actions of others. Exploring the role of k-level thinking in an asset pricing model allows us to determine optimal investment strategies when some investors behave suboptimally.
Level-k theory is based on the insight that inexperienced players may behave naïvely. More sophisticated players try to exploit naïve players by anticipating their actions and staying one step ahead. Even more sophisticated players may try to exploit those who believe that they are exploiting the naïve. Keynes concisely stated this logic: “Successful investing is anticipating the anticipations of others” (as quoted in [5], p. 105).
A salient choice for a naïve investor type is one who believes that past prices can predict future prices. The weakest form of the efficient market hypothesis states that past prices are not useful predictors of future prices. A common term for investors who use past prices to predict future prices is technical analysts. There is a large literature on technical analysis, but this literature has not considered the role of step-level thinking. Reviews of this literature are available in [6] and [7].
The belief that past prices predict future prices has a self-fulfilling aspect in that when enough investors believe that price will be increasing, they take actions that cause price to increase [8]. This self-fulfilling aspect creates opportunities for investors who can stay one step ahead of the naïve.
Efficient market theory can be thought of as a Nash equilibrium. As in many areas of economics, considerably more attention has been devoted to Nash equilibrium predictions than non-Nash solution concepts. The importance of examining non-Nash solution concepts comes from experimental work, which has shown that, for many strategic situations, behavior differs from Nash equilibria. This paper contributes to the literature on non-Nash solution concepts in finance.
We present a game theoretic model of financial investment that allows for investors of heterogeneous sophistication. Prices fluctuate and naïve investors believe that fluctuations transmit information about the fundamental value of the asset. Investors move prices toward their expectations of the future price, but, due to risk aversion, they do not trade aggressively enough to equate the current price with their expectation of future price. In this model, we assume that prices are determined by the equilibrium of a Walrasian tâtonnement process so that price equates supply and demand in every period. In other words, while the actions of investors are not at Nash equilibrium, the price is at an equilibrium value. This assumption prevents gains to technical analysts who are able to estimate the price adjustment mechanism in the presence of prices that are slow to adjust to equilibrium. We show that, in a Nash equilibrium, no investors use technical analysis and any investor who uses technical analysis will lower her expected utility. Moreover, we show that in the presence of a large number of technical analysts, technical analysts (and investors who worry about the effects of technical analysts) receive greater average utility than Nash-type investors.
We do not attempt to explain behavior under learning. Learning has been explored in similar models without step-level thinking [9-11]. The possible continued presence of naïve investors allows for investors who try to stay one step ahead of the naïve. This can be thought of as the interaction between investors in different stages of the learning process. In large markets, there will be continual entry of new investors who will interact with more experienced investors.
Equilibrium models in which investors try to predict the predictions of others have been previously explored [12]. A disequilibrium approach allows for the possibility of sophisticated investors exploiting naïveté. A model of disequilibrium also illuminates optimal investment behavior in markets with naïve investors.
In the following section, we describe level-k theory and models of heterogeneous sophistication. We present a simple model of asset pricing with heterogeneous sophistication in Section 3. Section 4 concludes the paper.
2. Heterogeneous Sophistication
Level-k theory can be illustrated through the example of a ρ-beauty contest. Players simultaneously select a number between 0 and 100. The winner is whoever selects a value that is closest to ρ times the average choice, where ρ is positive and less than one. In the event of a tie, the winner is randomly selected from those with the closest numbers. Through iterative dominance, it follows that the unique Nash equilibrium of this game is that all players pick 0.
We begin our level-k analysis by defining a naïve-type player. A naïve, non-strategic strategy for this game may be to select a number uniformly from the interval [0,100]. We will refer to this type of player as “level-0.” A “level-1” player is one who wants to take advantage of these level-0 players. This player believes that all other players follow the leve-0 strategy of picking randomly and so the average will be 50. Given this belief and ignoring her own effect on the average, a level-1 player picks (ρ × 50). A “level-2” player is one who believes that other players are level-1 type and picks (ρ2 × 50). Continuing this logic, a level-k player would pick (ρk × 50). As k approaches infinity, a level-k player’s strategy approaches the strategy that a player would pick in Nash equilibrium.
In pioneering work, Nagel [1] conducted experiments with ρ-beauty contests and found “depths of reasoning” to play an important role in this type of strategic setting. Other experimental designs that involve iterated elimination of dominated strategies have found evidence in favor of level-k thinking [13].
Level-k theory has been used to explain a number of phenomena. Overbidding in common value auctions can be seen as resulting from level-k thinking. Crawford and Iriberri [14] showed that when a level-1 type believes that level-0 types are bidding randomly, the level-1 type believes that winning the auction reveals no information about value. This belief results in a level-1 type over- bidding relative to equilibrium. Level-k thinking has also illuminated behavior in “hide-and-seek” games, which require anticipating and matching the behavior of a rival [15].
This work on heterogeneous sophistication is related to the concept of overconfidence. Investors using level-k thinking are overconfident in the sense that they believe they are able to correctly anticipate the sophistication of other investors and stay one step ahead of them. Previous work in finance has modeled overconfident investors as believing their private information is more precise than it truly is [16-18]. This type of overconfidence can generate excess volatility (as in [16]). Technical analysts believe their price predictions to be more accurate than they are. But here we allow not only for investors who overweigh private information, but also for investors who try to exploit these naïve investors.
3. Asset Price and Market Volatility
We base our model of market volatility on DeLong, Shleifer, Summers, and Waldmann [19]. We consider a two-period overlapping generations model with a continuum of risk averse investors. Young investors receive an endowment of Ω in at the beginning of their life. Nothing is consumed in the “young” state. The young investor decides how to allocate her endowment between a risky asset and a safe asset. When the investor reaches the “old” state, all of her wealth is turned into consumption.
The safe asset will always return r. The risky asset will pay a dividend dt, that is known at time t, and will be sold in the second period for a price, pt+1, that is not yet known. So buying λt shares of the risky asset will yield the investor λt(pt+1 + dt) from her investment. After buying λt shares of the risky asset, the investor has (Ω - λt pt) left to invest in the safe asset. We can express the investor’s wealth in her final period as
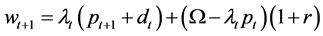 (1)
(1)
Dividends are equal to their value in the previous period plus an independently and identically distributed Gaussian error term, i.e.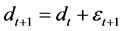 . The variance of the error term ε is denoted by
. The variance of the error term ε is denoted by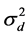 . As it will be shown below, pt+1 is a linear function of dt+1, which means that pt+1 is normally distributed.
. As it will be shown below, pt+1 is a linear function of dt+1, which means that pt+1 is normally distributed.
Investors are worried about their level of wealth in their final period and exhibit constant absolute risk aversion. The investor’s utility function is
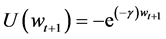 , (2)
, (2)
where γ is the coefficient of absolute risk aversion. Since wealth follows a normal distribution,
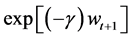
follows a log normal distribution. The investor purchases λt shares of the risky asset, where λt is equal to
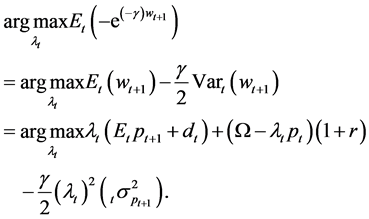
The term
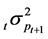 is the variance of next period’s price conditional on her information set at time t. Next period’s price, pt+1, will be treated as a random variable because it depends on next period’s dividend, dt+1, which is also not yet known.
is the variance of next period’s price conditional on her information set at time t. Next period’s price, pt+1, will be treated as a random variable because it depends on next period’s dividend, dt+1, which is also not yet known.
We treat pt as a parameter because a Walrasian auctioneer will announce the value of pt that equates supply and demand.
From the first order condition for utility maximization, we find
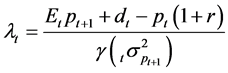 . (3)
. (3)
Let st denote the per capita supply of the risky asset. Equating supply and demand at time t reveals today’s price as
 . (4)
. (4)
Beliefs about next period’s price appear in the equation for price as it plays a crucial role in determining demand.
If we assume that the per capita supply of the risky asset, st=s0, is constant, it follows that the expectation of next period’s price will be
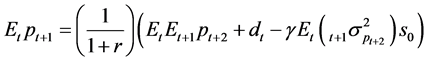 . (5)
. (5)
From this price equation we can find the variance of next period’s price conditional on her information set at time t.
 (6)
(6)
We will conjecture that there exists an equilibrium in which future prices cannot be predicted with past prices and show that this is a Nash equilibrium. This equilibrium corresponds to the efficient market hypothesis in that there is no available information that can assist an investor in forming expectations about expected return and variance. In this equilibrium, variance is constant and equal to
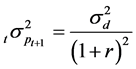 . (7)
. (7)
We find the expectation of next period’s price to be
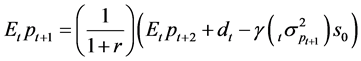 . (8)
. (8)
We are now ready to state our first theorem.
Theorem 1 There is a Nash equilibrium in which the price of the risky asset follows a random walk.
We can see this by combining Equations (4), (7), and (8) and iterating forward to find
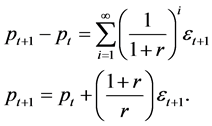
We will refer to the price that occurs in the Nash equilibrium of this game as the fundamentals price.
A belief that a future period’s price will be anything other than the last observed price decreases the investor’s expected utility. Using technical analysis can only lower an investor’s welfare when all other investors are behaving according to Nash equilibrium. To see this, suppose that a single investor believes that price tomorrow will be equal to (Etpt+1 + bt) where bt is the bias of the investors estimate. From Equations (2) and (3), we can express the investors’ utility as
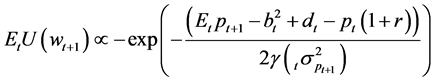 . (9)
. (9)
Expected utility is maximized when bias equals zero.
We can now ask what price would occur without the assumption of common knowledge of rationality. Level-k theory will provide insight into the actions of investors who differ in their sophistication.
3.1. Asset Price with Level-k Thinking
Expected price and perceived variance play crucial roles in determining an investor’s demand for the risky asset. An investor’s beliefs about risk and return may be at equilibrium or may be based on beliefs about other investors. Here we only consider the case when only price expectations are based on beliefs of other investors. The variance of the risky asset’s price is correctly estimated by investors.
In his original work on efficient portfolios, Markowitz [20] said that beliefs about risk and return “should combine statistical techniques and the judgment of practical men.” Markowitz goes on to say that the judgment of practical men should consider “factors or nuances not taken into account by the formal computations.” Following Markowitz’s advice, technical analysts, our level-0 types, believe that recent prices reveal useful information for predicting future prices (and thus returns). We do not specify how level-0’s expectation of tomorrow’s price is influenced by recent prices. Instead, we explore how expectations based on past prices affect price levels and volatility.
3.1.1. Level-0
A level-0 investor believes that she can use technical analysis to gain insight into next period’s price. Level-0’s expectation is a smooth function of recent prices. For simplicity, we will assume that the technical rule used by level-0 does not change over time.
With all level-0s the price of the risky asset is given by
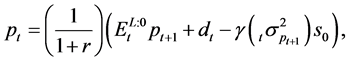 (10)
(10)
where
 is level-0’s expectation of next period’s price.
is level-0’s expectation of next period’s price.
The variance of price under all level-0 types is found by using the delta method. (For a random variable xn with variance , the delta method approximation of the variance of f(xn) is
, the delta method approximation of the variance of f(xn) is

for f differentiable and nonzero at xn.)

We assume that level-0’s expectation of tomorrow’s price does not sway drastically in past prices so that
and thus variance is greater than the variance in Nash equilibrium,
The intuition for greater variance is that, because level-0 types cause price to depend on past prices, the risky asset becomes riskier and investors are allocating less savings toward the risky asset. The result is that there is more risk involved in investing in the risky asset but also greater expected return. Less demand for the risky asset lowers prices and increases return.
Price is moved toward level-0’s expectation of price, but price will not be equal to level-0’s expectation of price. When all investors are level-0 type, expected price is equal to

This value differs from expected price in Nash equilibrium by a level-0 type’s bias multiplied by 1/(1+r). Since 1/(1+r) is less than one, expected price differs from a fundamental value by less than the bias of level-0 types.
3.1.2. Higher Levels
A level-1 investor takes advantage of level-0’s influence on price by forming price expectations that are between the expectations of level-0 and Nash-types. Under the belief that all other investors are level-0 type, level-1 types form the expectation
Level-1 types are required to make a prediction of tomorrow’s level-0 type’s expectation. This is because tomorrow, at time (t + 1), level-0 types will have more price information available.
We saw in Equation (9) that an investor’s expected utility is decreasing in the bias of her price expectation. When all investors are level-0 type, the price expectation of a Nash-type investor will have bias equal to

Level-1 investors will have an expected bias of zero.
Following this logic, we can find the price of the risky asset that results when all investors are level-k type. Let us first define the term

We can now express the resulting price as

The unconditional variance of this price equals

We can see that price approaches the Nash equilibrium price as k goes to infinity,

3.2. Asset Price with Heterogeneous Sophistication
Suppose that, instead of believing that all investors are level-0 type, level-1 believes that some investors are level-0 type and some investors behave according to Nash equilibrium. Level-2 may believe that other investors are a combination of level-1 and Nash equilibrium type, and likewise for levels 3, 4, and so on. This complication can be easily adapted into our framework by analyzing the price that results under a given combination of types.
When μ proportion of other investors are level-0 and the remaining (1 − μ) proportion are Nash-type investors, the resulting price is
This price is a convex combination of the price that results from all level-0 types and the Nash equilibrium price. Variance is given by
when μ equals zero, this variance is the variance in Nash equilibrium. When μ equals one, this is the variance that results under all level-0 types. Variance is bounded between the variance under all level-0 types and the variance under all Nash-types. An investor who believes that μ proportion of other investors are level-0 and the remaining (1 − μ) proportion are Nash type investors forms the expectation
When all investors believe that μ proportion of other investors are level-0 and the remaining (1 − μ) proportion are Nash type investors, the resulting price is
The price that results is between the price that results under a population of investors who believe that all investors are level-0 type and the Nash equilibrium price. When all investors believe that μ proportion of other investors are level-0 and the remaining (1 − μ) proportion are Nash type investors, then the resulting price can be expressed as the price that would result with




Theorem 2 For any distribution of investors with heterogeneous sophistication, we can express price as resulting from a combination of only level-0 and Nash-type investors.
Proof. We know that price that results from investors who best respond to a mixture of level-0 and Nash-types can be expressed as a mixture of level-0 and Nash-types. A level-2 investor, who best responds to a mixture of level-1 types and Nash-types, knows that price under level-1 is a convex combination of price under level-0 and Nash-types. A level-2 type also best responds to a mixture of level-0 and Nash-types. This logic follows for higher types.
We have seen that, for any distribution of investor sophistication, it is possible to express price as resulting from a combination of only level-0 type and Nash type investors. When price is closer to the Nash equilibrium price, more weight is placed on the expectations of the Nash type of investors. This term μ provides a type of index of market-level naïveté. With an estimate of μ, we can derive expected price and the optimal investment in the risky asset.
Theorem 3 When we represent price as a combination of μ level-0 types and (1 − μ) Nash-type investors, higher values of μ imply greater variance and greater average return.
This last theorem follows from the equations for expected price and variance.
4. Conclusion
Efficient market theory can be characterized by a Nash equilibrium. We have learned that when there is a significant portion of investors who are incorporating past price information in their investment decisions, an investor can improve her expected utility by anticipating the effects of heterogeneous sophistication on the market. When the naïve believe that there are exploitable trends in asset prices, price is pushed toward these naïve expectations. In addition to creating opportunities for sophisticated investors to earn higher expected utility, market-level naïveté also increases market risk and return.
REFERENCES
[1] R. Nagel, “Unraveling in Guessing Games: An Experi- mental Study,” American Economic Review, Vol. 85, No. 5, 1995, pp. 1313-1326.
[2] A. Bosch-Domènech, J. G. Montalvo, R. Nagel and A. Satorra, “One, Two, (Three), Infinity, …: Newspaper and Lab Beauty-Contest Experiments,” American Economic Review, Vol. 92, No. 5, 2002, pp. 1687-1701. http://dx.doi.org/10.1257/000282802762024737
[3] D. O. Stahl and P. W. Wilson, “Experimental Evidence on Players’ Models of Other Players,” Journal of Eco- nomic Behavior & Organization, Vol. 25, No. 3, 1994, pp. 309-327. http://dx.doi.org/10.1016/0167-2681(94)90103-1
[4] D. O. Stahl and P. W. Wilson, “On Players’ Models of Other Players: Theory and Evidence,” Games and Economic Behavior, Vol. 10, No. 1, 1995, pp. 218-254. http://dx.doi.org/10.1006/game.1995.1031
[5] G. Bergman, “Isms,” Adams Media, New York, 2006.
[6] C.-H. Park and S. H. Irwin, “What Do We Know about the Profitability of Technical Analysis?” Journal of Eco- nomic Surveys, Vol. 21, No. 4, 2007, pp. 786-826. http://dx.doi.org/10.1111/j.1467-6419.2007.00519.x
[7] L. Menkhoff and M. P. Taylor, “The Obstinate Passion of Foreign Exchange Professional: Technical Analysis,” Journal of Economic Literature, Vol. 45, No. 4, 2007, pp. 936-972. http://dx.doi.org/10.1257/jel.45.4.936
[8] M. P. Taylor and H. Allen, “The Use of Technical Analy- sis in the Foreign Exchange Market,” Journal of Interna- tional Money and Finance, Vol. 1, No. 3, 1992, pp. 304- 314. http://dx.doi.org/10.1016/0261-5606(92)90048-3
[9] W. A. Brock and C. H. Hommes, “Heterogeneous Beliefs and Routes to Chaos in a Simple Asset Pricing Model,” Journal of Economic Dynamics and Control, Vol. 22, No. 89, 1998, pp. 1235-1274. http://dx.doi.org/10.1016/S0165-1889(98)00011-6
[10] C. Chiarella and X.-Z. He, “Heterogeneous Beliefs, Risk and Learning in a Simple Asset Pricing Model,” Compu- tational Economics, Vol. 19, 1, 2002, pp. 95-132. http://dx.doi.org/10.1023/A:1014957310778
[11] W. Branch and G. Evans, “Learning about Risk and Re- turn: A Simple Model of Bubbles and Crashes,” Ameri- can Economic Journal: Macroeconomics, Vol. 3, No. 3, 2011, pp. 159-191. http://dx.doi.org/10.1257/mac.3.3.159
[12] R. M. Townsend, “Forecasting the Forecasts of Others,” Journal of Political Economy, Vol. 91, No. 4, 1983, pp. 546-588. http://dx.doi.org/10.1086/261166
[13] M. Costa-Gomes, V. P. Crawford and B. Broseta, “Cog- nition and Behavior in Normal-Form Games: An Experi- mental Study,” Econometrica, Vol. 69, No. 5, 2001, pp. 11193-1235. http://dx.doi.org/10.1111/1468-0262.00239
[14] V. P. Crawford and N. Iriberri, “Level-k Auctions: Can a Nonequilibrium Model of Strategic Thinking Explain the Winner’s Curse and Overbidding in Private-Value Auc- tions?” Econometrica, Vol. 75, No. 6, 2007, pp. 1721- 1770. http://dx.doi.org/10.1111/j.1468-0262.2007.00810.x
[15] V. P. Crawford and N. Iriberri, “Fatal Attraction: Salience, Naïveté, and Sophistication in Experimental ‘Hide-and- Seek’ Games,” American Economic Review, Vol. 97, No. 5, 2007, pp. 1731-1750. http://dx.doi.org/10.1257/aer.97.5.1731
[16] T. Odean, “Volume, Volatility, Price, and Profit When All Traders Are Above Average,” Journal of Finance, Vol. 53, 6, 1998, pp. 1887-1934. http://dx.doi.org/10.1111/0022-1082.00078
[17] S. Gervais and T. Odean, “Learning to Be Overconfi- dent,” Review of Financial Studies, Vol. 14, 1, 2001, pp. 1-14. http://dx.doi.org/10.1093/rfs/14.1.1
[18] K. D. Daniel, D. Hirshleifer and A. Subrahmanyam, “In- vestor Psychology and the Market under- and Over-Re- actions,” Journal of Finance, Vol. 53, 6, 1998, pp. 1839- 1886. http://dx.doi.org/10.1111/0022-1082.00077
[19] B. DeLong, A. Shleifer, L. Summers and R. Waldmann, “Noise Trader Risk in Financial Markets,” Journal of Po- litical Economy, Vol. 98, No. 4, 1990, pp. 703-738. http://dx.doi.org/10.1086/261703
[20] H. Markowitz, “Portfolio Selection,” Journal of Finance, Vol. 7, No. 1, 1952, pp. 77-91. http://dx.doi.org/10.2307/2975974







