Journal of Mathematical Finance
Vol.4 No.2(2014), Article ID:43337,12 pages DOI:10.4236/jmf.2014.42012
The Fundamental Theorem of Asset Pricing with either Frictionless or Frictional Security Markets
1Faculty of Business Administration, The University of Regina, Regina, Canada
2School of Finance, Renmin University of China, Beijing, China
Email: helen.huang@uregina.ca, *szhang@ruc.edu.cn, shunning.zhang@gmail.com
Received November 21, 2013; revised January 6, 2014; accepted January 22, 2014
ABSTRACT
This paper studies asset pricing in arbitrage-free financial markets in general state space (both for frictionless market and for market with transaction cost). The mathematical formulation is based on a locally convex topological space for weakly arbitrage-free securities’ structure and a separable Banach space for strictly arbitragefree securities’ structure. We establish, for these two types of spaces, the weakly arbitrage-free pricing theorem and the strictly arbitrage-free pricing theorem, respectively.
Keywords:The First Fundamental Valuation Theorems; Transaction Costs; Weak Arbitrage-Freeness; Strict Arbitrage-Freeness; Arbitrage-Free Pricing Theory; Locally Convex Topological Space; Separable Banach Space
1. Introduction
Arbitrage-free asset pricing theory is of fundamental importance in neo-classical finance. In this paper, we consider it in a setting of general state spaces, in particular, locally convex topological space for weakly arbitrage-free security markets, and separable Banach space for strictly arbitrage-free security markets. We deal with both frictionless and frictional security markets.
In the study of mathematical economics, arbitrage-free conditions have always been an important first step toward the general equilibrium theorem with incomplete asset markets (Duffie and Shafer [1,2]; Geanakoplos [3]; Geanakoplos and Shafer [4]; Hirsch, Magill and Mas-Colell [5]; Husseini, Lasry and Magill [6]; and Magill and Shafer [7]). Since the 1980s, for finite period economies, no-arbitrage pricing theory has been applied by various authors to prove the existence of general equilibrium for stochastic economies with incomplete financial markets (Duffie [8-10]; Florenzano and Gourdel [11]; Magill and Shafer [7]; Werner [12,13]; and Zhang [14]). In those works, the finite number of possible states of nature and the finite-dimensional commodity space are usually assumed in order for the proofs to be carried out for the general equilibrium model with incomplete financial markets. Our model considers a general state space which may have an infinite number of states.
Many mathematical economists usually apply Stiemke’s Lemma, a strict version of Farkas-Minkowski’s Lemma, to study the asset pricing theory with no-arbitrage conditions, for example, discrete-time models of dynamic asset pricing theory (Duffie [9,10]) and the theory of economic equilibrium with incomplete asset markets (Geanakoplos [3]; Geanakoplos and Shafer [4]; Hirsch, Magill and Mas-Colell [5]; Husseini, Lasry and Magill [6]; and Magill and Shafer [7]) where the commodity space is of finite dimension. Farkas-Minkowski’s Lemma and Stiemke’s Lemma are in essence the mathematical counter part of the asset pricing theory with no-arbitrage conditions. In this paper, we obtain extensions (to the general state space in our discussion) of Farkas-Minkowski’s Lemma and Stiemke’s Lemma by applying Clark’s separating hyperplane theorems (Clark [15,16]), and thus establish our main results.
Harrison and Kreps [17] initiated the study of martingales and arbitrage in multiperiod security markets. They first introduced general theory of arbitrage in a two-period economy with uncertainty, and then extended it to the models of multiperiod security markets and the models of continuous-time securities markets. Kreps [18] studied arbitrage and equilibrium in economies with infinitely many commodities and presented an abstract analysis of “arbitrage” in economies that have infinite dimensional commodity space. Harrison and Pliska [19] studied martingales and stochastic integrals in the theory of continuous trading. Dalang, Morton and Willinger [20] studied equivalent martingale measures and no-arbitrage in stochastic securities market models. Back and Pliska [21] studied the fundamental theorem of asset pricing with an infinite state space and showed some equivalent relations on arbitrage. Jacod and Sgiryaev [22] studied local martingales and the fundamental asset pricing theorems in the discrete-time case. These papers studied fundamental theorems of asset pricing in multiperiod financial models with the help of techniques from stochastic analysis. Our work is based on separating hyperplane theorems and does not rely on assumptions made for stochastic analysis to be able to carry out in the above models.
Friction in markets has attracted attention of several works in this field recently. Chen [23] examined the incentives and economic roles of financial innovation and at the same time studied the effectiveness of the replication-based arbitrage valuation approach in frictional economies (the friction means holding constraints). Jouini and Kallal [24] derived the implications of the absence of arbitrage in securities markets models where traded securities are subject to short-sales constraints and where the borrowing and lending rates differ, and showed that a securities price system is arbitrage free if and only if there exists a numeraire and an equivalent probability measure for which the normalized (by the numeraire) price processes of traded securities are supermartingales. Jouini and Kallal [25] derived the implications from the absence of arbitrage in dynamic securities markets with bid-ask spreads. The absence of arbitrage is equivalent to the existence of at least an equivalent probability measure that transforms some process between the bid and the ask price processes of traded securities into a martingale. Pham and Touzi [26] addressed the problem of characterization of no arbitrage (strictly arbitrage-free) in the presence of friction in a discrete-time financial model, and extended the fundamental theorem of asset pricing under a non-degeneracy assumption. The friction is described by the transaction cost rates for purchasing and selling the securities. We follow the model for transaction costs from Pham and Touzi [26], and then extend the first fundamental valuation theorems of asset pricing from frictionless security markets to frictional security markets, for general state space. Again, their stochastic analysis method requires stronger assumptions than ours. In addition, their arbitrage-free conditions are slightly different from ours based on that of Duffie [9].
Section 2 presents our model without transaction costs, we define the weakly arbitrage-free security markets and strictly arbitrage-free security markets, following Duffie [9]. In the next two sections, we establish the first fundamental valuation theorem of asset pricing (a necessary and sufficient condition for arbitrage-freeness) with weakly arbitrage-free security markets in Section 3 and strictly arbitrage-free security markets in Section 4. In the rest of the paper we extend our work to markets with transaction costs, following the model of Pham and Touzi [26]. The transaction cost model is presented in Section 5, and the corresponding first fundamental valuation theorems of asset pricing are done in Sections 6 and 7. Section 8 concludes our article with some remarks.
2. Frictionless Security Markets
We consider a two-period model (dates 0 and 1) with uncertainty over the states of nature in the date 1. The unknown nature of the future is represented by a general set  of possible states of nature, one of which will be revealed as true. Here we make no assumption about the probability of these states. The
of possible states of nature, one of which will be revealed as true. Here we make no assumption about the probability of these states. The 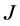 securities are given by a return “matrix”
securities are given by a return “matrix” , where
, where  denotes the number of units of account paid by security
denotes the number of units of account paid by security . Let
. Let 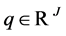 denote the vector of prices of
denote the vector of prices of  securities. A portfolio
securities. A portfolio 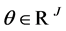 has market value
has market value  and payoff
and payoff .
.
Let  be a topological space consisting of processes in
be a topological space consisting of processes in ,
,  is the positive cone of
is the positive cone of . Let
. Let  be the dual space composed of the continuous linear functionals on
be the dual space composed of the continuous linear functionals on ,
,  the positive cone of the space
the positive cone of the space  (the space of all positive continuous linear functionals on
(the space of all positive continuous linear functionals on ) and
) and  the interior of the cone
the interior of the cone  (the space of all strictly positive continuous linear functionals on
(the space of all strictly positive continuous linear functionals on ):
): .
.
In this paper, we assume  for
for . Then
. Then . Our proof must adopt the following notation
. Our proof must adopt the following notation  and
and .
.
[Definition ]">1] The frictionless market  is weakly arbitrage-free if any portfolio
is weakly arbitrage-free if any portfolio  of securities has a positive market value
of securities has a positive market value  whenever it has a positive payoff
whenever it has a positive payoff .
.
[Definition ]">2] The frictionless market  is strictly arbitrage-free if (1) any portfolio
is strictly arbitrage-free if (1) any portfolio  of securities has a strictly positive market value
of securities has a strictly positive market value 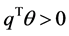 whenever it has a positive non-zero payoff
whenever it has a positive non-zero payoff ; and (2) any portfolio
; and (2) any portfolio  of securities has a zero market value
of securities has a zero market value  whenever it has a zero payoff
whenever it has a zero payoff .
.
Definition 2 implies Definition 1 obviously. We follow the definition for arbitrage opportunity as provided by Duffie [9,]">10]. An arbitrage is a portfolio  with either (1)
with either (1)  and
and , or (2)
, or (2)  and
and . That is to say, the frictionless market
. That is to say, the frictionless market  admits an arbitrage opportunity if there exists an portfolio
admits an arbitrage opportunity if there exists an portfolio 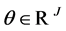 of securities such that either (1)
of securities such that either (1)  and
and , or (2)
, or (2) 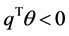 and
and
 . Consequently, we can define the strictly arbitrage-free (no arbitrage) frictionless market
. Consequently, we can define the strictly arbitrage-free (no arbitrage) frictionless market  as follows.
as follows.
[Definition 2¢] The frictionless market  is strictly arbitrage-free if (1) any portfolio
is strictly arbitrage-free if (1) any portfolio  of securities has a strictly positive market value
of securities has a strictly positive market value  whenever it has a positive non-zero payoff
whenever it has a positive non-zero payoff ; and (2) any portfolio
; and (2) any portfolio  of securities has a positive market value
of securities has a positive market value  whenever it has a positive payoff
whenever it has a positive payoff .
.
[Lemma ]">1] Definitions 2 and 2’ are equivalent.
An arbitrage is therefore, in effect, a portfolio offering “something for nothing”. Not surprisingly, an arbitrage is naturally ruled out in reality. And this fact gives a characterization of security prices as follows: A valuation functional is a functional  for the weakly arbitrage-free frictionless market
for the weakly arbitrage-free frictionless market  with consistency
with consistency ; and a functional
; and a functional 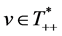 for the strictly arbitrage-free frictionless market
for the strictly arbitrage-free frictionless market 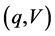 with consistency
with consistency , where
, where . The valuation functional is called to be a positive linear consistent valuation operator for the weakly arbitrage-free frictionless market, a strictly positive linear consistent valuation operator for the strictly arbitrage-free frictionless market, respectively.
. The valuation functional is called to be a positive linear consistent valuation operator for the weakly arbitrage-free frictionless market, a strictly positive linear consistent valuation operator for the strictly arbitrage-free frictionless market, respectively.
The idea of arbitrage and the absence of arbitrage opportunities is fundamental in finance. The strict arbitrage-freeness is important in the study of general equilibrium theory with incomplete asset markets (Husseini, Lasry and Magill [6]; Werner [13]; and Magill and Shafer [7]). Theorem 2 to be presented in the following is an important step in the study of equilibrium for economies with general state spaces considered in our work. The principal mathematical tool applied here is the Separating Hyperplane Theorems of Clark [15] and [16].
[Fact ]">1] (Clark [16]) Suppose  and
and  are non-empty disjoint convex cones in a locally convex topological vector space
are non-empty disjoint convex cones in a locally convex topological vector space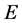 . Then there exists a non-zero continuous linear functional
. Then there exists a non-zero continuous linear functional  separating
separating
 from
from :
:  for all
for all  and
and  for all
for all  if and only if
if and only if . Moreoverif
. Moreoverif , then for any
, then for any 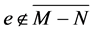 we may select
we may select  so that
so that .
.
[Fact ]">2] (Clark [15]) Suppose  and
and 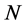 are non-empty convex cones (with vertices at the origin) in a separating Banach space
are non-empty convex cones (with vertices at the origin) in a separating Banach space . Then there exists a non-zero continuous linear functional
. Then there exists a non-zero continuous linear functional  strictly separating N from M:
strictly separating N from M:  for all
for all  and
and  for all
for all  if and only if
if and only if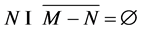 .
.
Fact 1 and 2 will be used to prove Theorems 1 and 2 in Sections 3 and 4, Theorems 3 and 4 in Sections 6 and 7, respectively. We assume , which is a topological space, then
, which is a topological space, then  is the positive cone of
is the positive cone of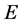 , which is a positive closed convex cone of
, which is a positive closed convex cone of 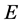 with its vertex at the origin. The marketed subspace
with its vertex at the origin. The marketed subspace

is a linear subspace of the space .
.
3. Weakly Arbitrage-Free Security Valuation Theorem with Frictionless Security Markets
In this section, we assume that 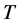 is a locally convex topological space.
is a locally convex topological space.
[Proposition 1] The frictionless market 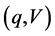 is weakly arbitrage-free if and only if
is weakly arbitrage-free if and only if .
.
Proof. 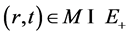 implies that there exists
implies that there exists  such that
such that  and
and . On the other hand,
. On the other hand,  implies that
implies that  from Definition 1, then
from Definition 1, then . Thus
. Thus  and
and
 , that is,
, that is, .
.
Conversely, if there exists  such that
such that  and
and , then
, then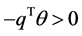 . Thus
. Thus
 and
and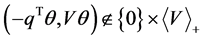 .
.
This is a contradiction! Therefore the frictionless market  is weakly arbitrage-free. Q.E.D.
is weakly arbitrage-free. Q.E.D.
[Theorem 1] The frictionless market 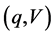 is weakly arbitrage-free if and only if there exists a positive functional
is weakly arbitrage-free if and only if there exists a positive functional 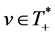 satisfying
satisfying .
.
Proof. Both 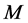 and
and 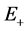 are closed and convex cones of
are closed and convex cones of  with their vertices at the origin.
with their vertices at the origin.
The frictionless market 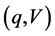 is weakly arbitrage-free if and only if
is weakly arbitrage-free if and only if . Note that
. Note that
 is a convex set. Let
is a convex set. Let , then
, then  is a (non-empty) convex set. Both
is a (non-empty) convex set. Both 
and  are non-empty disjoint convex cones
are non-empty disjoint convex cones .
.  implies
implies . Clark [16] stated that there exists a non-zero continuous linear functional
. Clark [16] stated that there exists a non-zero continuous linear functional  separating
separating  from
from , that is,
, that is,  for all
for all  and
and  for all
for all . Moreover,
. Moreover, .
.
 is a positive continuous linear functional on
is a positive continuous linear functional on . In fact, for any
. In fact, for any  and natural number
and natural number ,
,  and
and . Therefore,
. Therefore, . Thus
. Thus
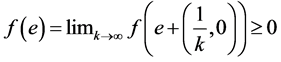 .
.
That is,  is a positive continuous linear functional on
is a positive continuous linear functional on .
.
Thus  is represented by some
is represented by some  and
and  by
by 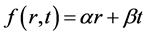 for any
for any . In fact,
. In fact,  is represented by some
is represented by some  and
and  by
by  for any
for any . The fact that
. The fact that
 implies
implies . If
. If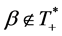 , then there exists
, then there exists 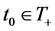 such that
such that . Take
. Take
 , then
, then  and
and . The contradiction means
. The contradiction means .
.
Since  is a linear space,
is a linear space, 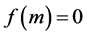 for all
for all , that is,
, that is,  for all
for all . Then
. Then
 . And therefore, the vector
. And therefore, the vector  is that we want.
is that we want.
The converse is obvious. Q.E.D.
[Remark 1] If  is a finite set, then
is a finite set, then  is an Euclidean space, Definition 1 is the usual concept of weak arbitrage-freeness. Theorem 1 is the well-known Farkas-Minkowski’s Lemma (Duffie [9]; Farkas [27] and Franklin [28]).
is an Euclidean space, Definition 1 is the usual concept of weak arbitrage-freeness. Theorem 1 is the well-known Farkas-Minkowski’s Lemma (Duffie [9]; Farkas [27] and Franklin [28]).
[Remark 2] Theorem 1 (The Extension of Farkas-Minkowski’s Lemma) means that the present value of the securities prices at date 0 is the value of their returns at date 1.
4. Strictly Arbitrage-Free Security Valuation Theorem with Frictionless Security Markets
In this section, we assume that  is a separable Banach space. We prove Proposition 2 and Theorem 2 by using Definition 2 of the strictly arbitrage-free frictionless market
is a separable Banach space. We prove Proposition 2 and Theorem 2 by using Definition 2 of the strictly arbitrage-free frictionless market .
.
[Proposition 2] The frictionless market  is strictly arbitrage-free if and only if
is strictly arbitrage-free if and only if  and
and  intersect precisely at
intersect precisely at , that is,
, that is, .
.
Proof.  implies that there exists
implies that there exists  such that
such that  and
and . If
. If , then
, then  from Definition 2 (1),
from Definition 2 (1),  , a contradiction! If
, a contradiction! If , then
, then  from Definition 2 (2),
from Definition 2 (2), 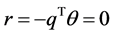 and
and . Thus
. Thus . And hence,
. And hence, .
.
For sufficiency, we must consider two cases: (1) If there exists 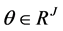 such that
such that  and
and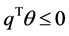 , then
, then  and
and , a contradiction. Therefore, any portfolio
, a contradiction. Therefore, any portfolio  of securities has a positive non-zero market value
of securities has a positive non-zero market value  whenever it has a positive payoff
whenever it has a positive payoff . (2)
. (2)
If there exists  such that
such that  and
and , we discuss the problem for the following two settings. (2.1) When
, we discuss the problem for the following two settings. (2.1) When , then
, then , thus
, thus . This is a contradiction! (2.2)
. This is a contradiction! (2.2)
When , then
, then  and
and , thus
, thus . This is a contradiction! The two contradictions mean that the frictionless market
. This is a contradiction! The two contradictions mean that the frictionless market 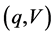 is strictly arbitrage-free. Q.E.D.
is strictly arbitrage-free. Q.E.D.
[Theorem 2] The frictionless market  is strictly arbitrage-free if and only if there exists a strictly positive functional
is strictly arbitrage-free if and only if there exists a strictly positive functional  satisfying
satisfying .
.
Proof. Both  and
and  are closed and convex cones of
are closed and convex cones of  with their vertices at the origin.
with their vertices at the origin.
Since 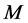 is a polyhedral (convex) cone in
is a polyhedral (convex) cone in  and
and  is a closed convex cone of
is a closed convex cone of , then
, then  is a closed convex cone from Lemma of Clark [15], that is,
is a closed convex cone from Lemma of Clark [15], that is, . Thus
. Thus  is a closed convex cone
is a closed convex cone .
.
The frictionless market  is strictly arbitrage-free if and only if
is strictly arbitrage-free if and only if . We claim that
. We claim that
 . On the contrary, we assume that there exists
. On the contrary, we assume that there exists then
then  and
and  for
for  and
and . Thus
. Thus
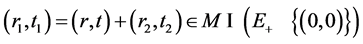 contradicting the conclusion
contradicting the conclusion  and
and .
.
Note that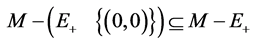 . It follows that
. It follows that . Thus
. Thus
 . Since both
. Since both  and
and  are non-empty convex cones with vertices at the origin in the separable Banach space
are non-empty convex cones with vertices at the origin in the separable Banach space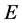 , Theorem 5 in Clark [15] states that there exists a non-zero continuous linear functional
, Theorem 5 in Clark [15] states that there exists a non-zero continuous linear functional  on
on  strictly separating
strictly separating  from
from , that is,
, that is,  for all
for all  and
and  for all
for all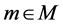 .
.
The condition  for all
for all  implies that
implies that  is a strictly positive continuous linear functional on
is a strictly positive continuous linear functional on . Thus
. Thus  is represented by some
is represented by some  and
and  by
by  for any
for any .
.
Since  is a linear space,
is a linear space,  for all
for all , that is,
, that is, 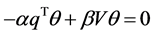 for all
for all . It follows that
. It follows that . The vector
. The vector  is that we want.
is that we want.
The converse is again obvious. Q.E.D.
[Remark 1] If  is a finite set, then
is a finite set, then 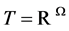 is an Euclidean space, Definition 1 is the usual concept of strict arbitrage-freeness. Theorem 2 is the well-known Stiemke’s Lemma (Duffie [9,10]).
is an Euclidean space, Definition 1 is the usual concept of strict arbitrage-freeness. Theorem 2 is the well-known Stiemke’s Lemma (Duffie [9,10]).
[Remark 2] Theorem 2 (The Extension of Stiemke’s Lemma) means that the present value of the securities prices at date 0 is the value of their returns at date 1.
[Remark 3] If  where
where 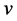 is a linear functional on
is a linear functional on , we can prove Theorem 2 by Kreps [18]. The sufficient condition is obvious, we only need prove the necessary condition. Take
, we can prove Theorem 2 by Kreps [18]. The sufficient condition is obvious, we only need prove the necessary condition. Take , then any element
, then any element  is of the form
is of the form  where
where . Take
. Take  as a linear functional on
as a linear functional on  solving the equation
solving the equation  for all
for all , i.e.
, i.e.  and take
and take . If the frictionless market
. If the frictionless market  is strictly arbitrage-free, then the pair
is strictly arbitrage-free, then the pair  admits no free lunches. Kreps’ conditions (4.7) and (4.10) are applied, then the pair
admits no free lunches. Kreps’ conditions (4.7) and (4.10) are applied, then the pair  is
is  -viable from Theorem 3 (Kreps [18]), that is, the pair
-viable from Theorem 3 (Kreps [18]), that is, the pair 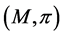 has the extension property for
has the extension property for . Thus the necessary condition is obtained.
. Thus the necessary condition is obtained.
5. Frictional Security Markets
Suppose that there are transaction costs in the trading, the coefficients  and
and 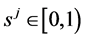 are respectively the transaction cost rates for purchasing and selling the security
are respectively the transaction cost rates for purchasing and selling the security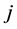 . Then the algebraic cost induced by (buying) a position
. Then the algebraic cost induced by (buying) a position  units of security
units of security 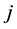 is
is 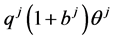 and the algebraic gain induced by (selling) a position
and the algebraic gain induced by (selling) a position  units of security
units of security 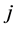 is
is . We introduce the functions
. We introduce the functions  defined by
defined by

and the functions  defined by
defined by
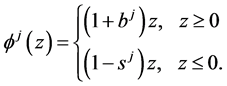
Then .
.
For any integer , a function
, a function  is subliner if, for any
is subliner if, for any ,
,  ,
,  and
and ,
,

The function  is sublinear, and hence convex. Therefore the function
is sublinear, and hence convex. Therefore the function  is also sublinear, and hence convex.
is also sublinear, and hence convex.
The total cost or gain induced by (trading) a portfolio  is
is . We define the function
. We define the function  by
by

Then the total cost or gain induced by (trading) a portfolio  is
is . As we know, the function
. As we know, the function  is sublinear, and hence convex.
is sublinear, and hence convex.
[Definition ]">3] The frictional market  is weakly arbitrage-free if any portfolio
is weakly arbitrage-free if any portfolio  of securities has a positive total cost or gain
of securities has a positive total cost or gain  whenever it has a positive payoff
whenever it has a positive payoff .
.
We note that Definitions 2 and 2’ are equivalent. However, in the presence of transaction costs, the corresponding Definitions 4 and 4’ (as follows) are not. We establish Theorem 4 for Definition 4’ of the strictly arbitrage-free frictional market .
.
[Definition ]">4] The frictional market 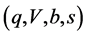 is strictly arbitrage-free if (1) any portfolio
is strictly arbitrage-free if (1) any portfolio  of securities has a strictly positive total cost or gain
of securities has a strictly positive total cost or gain  whenever it has a positive non-zero payoff
whenever it has a positive non-zero payoff ; and (2) any portfolio
; and (2) any portfolio 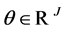 of securities has a zero total cost or gain
of securities has a zero total cost or gain  whenever it has a zero payoff
whenever it has a zero payoff .
.
[Definition 4’] The frictional market 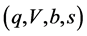 is strictly arbitrage-free if (1) any portfolio
is strictly arbitrage-free if (1) any portfolio  of securities has a strictly positive total cost or gain
of securities has a strictly positive total cost or gain 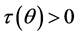 whenever it has a positive non-zero payoff
whenever it has a positive non-zero payoff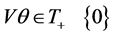 ; and (2) any portfolio
; and (2) any portfolio  of securities has a positive total cost or gain
of securities has a positive total cost or gain  whenever it has a positive payoff
whenever it has a positive payoff .
.
Definition 4 obviously implies Definition 4’. Definition 4’ does not imply Definition 4 because of the presence of friction. In the frictionless model, we define the marketed subspace
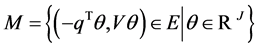
of the space  to prove the first fundamental theorems of asset pricing. In the frictional model, we can’t consider the corresponding marketed “subspace”
to prove the first fundamental theorems of asset pricing. In the frictional model, we can’t consider the corresponding marketed “subspace” . In fact, this marketed “subspace”
. In fact, this marketed “subspace”
isn’t a subspace of the space . Instead, we define the subset
. Instead, we define the subset  in the space
in the space  as follows
as follows

[Lemma 2]  is a closed and convex cone in the space
is a closed and convex cone in the space .
.
Proof.  is a closed cone obviously since the function
is a closed cone obviously since the function  is continuous and sublinear.
is continuous and sublinear.
For any  and
and , there exist
, there exist  and
and  such that
such that ,
,
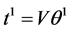 and
and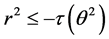 ,
, . Thus
. Thus  since the function
since the function  is sublinear, and
is sublinear, and . Therefore
. Therefore . Since
. Since  is a cone,
is a cone,  is convex. Q.E.D.
is convex. Q.E.D.
For simplicity, we use the following notations in the subsequent sections.
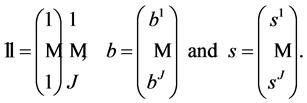
We define the box product of two vectors 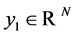 and
and  by
by
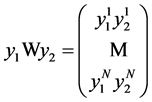
6. Weakly Arbitrage-Free Security Valuation Theorem with Frictional Security Markets
In this section, we assume that  is a locally convex topological space.
is a locally convex topological space.
[Proposition ]">3] The frictional market 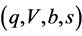 is weakly arbitrage-free if and only if
is weakly arbitrage-free if and only if .
.
Proof.  implies that there exists
implies that there exists 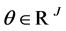 such that
such that  and
and . On the other hand,
. On the other hand,  implies that
implies that  from Definition 3. Then
from Definition 3. Then  and
and , that is,
, that is, .
.
Conversely, if there exists  such that
such that  and
and , then
, then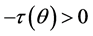 . Thus
. Thus
 and
and .
.
This is a contradiction! Therefore, any portfolio  of securities has a positive total cost or gain
of securities has a positive total cost or gain 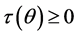 whenever it has a positive payoff
whenever it has a positive payoff . Q.E.D.
. Q.E.D.
[Remark] The proof of Proposition 3 only requires the property that  is a closed and convex cone in the space
is a closed and convex cone in the space 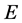 and doesn’t need the explicit definition of the function
and doesn’t need the explicit definition of the function , so does Proposition 3.
, so does Proposition 3.
[Theorem ]">3] The frictional market  is weakly arbitrage-free if and only if there exists a positive functional
is weakly arbitrage-free if and only if there exists a positive functional  satisfying
satisfying

Proof. Both  and
and  are closed and convex cones of
are closed and convex cones of  with their vertices at the origin.
with their vertices at the origin.
The frictional market  is weakly arbitrage-free if and only if
is weakly arbitrage-free if and only if . Note that
. Note that  is a convex set. Let
is a convex set. Let , then
, then  is a (non-empty) convex set. Both
is a (non-empty) convex set. Both 
and  are non-empty disjoint convex cones,
are non-empty disjoint convex cones, .
.  implies
implies
 . Clark [16] stated that there exists a non-zero continuous linear functional
. Clark [16] stated that there exists a non-zero continuous linear functional  separating
separating  from
from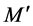 , that is,
, that is,  for all
for all  and
and  for all
for all . Moreover,
. Moreover, .
.
From the proof of Theorem 1,  is a positive continuous linear functional on
is a positive continuous linear functional on , and
, and  is represented by some
is represented by some 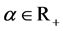 and
and  by
by 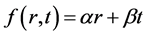 for any
for any .
.
On the other hand, the fact that  for all
for all  implies
implies  for all
for all 
and  for
for . Then
. Then  for all
for all . And hence we have
. And hence we have

for all . For each
. For each , assigning
, assigning , we have
, we have

that is, . Thus
. Thus

For each , we assign
, we assign  instead, it follows that
instead, it follows that

that is, . Thus
. Thus
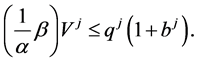
Therefore, for any ,
,

The vector  is thus what we want:
is thus what we want:
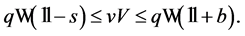
Conversely, assume that there exists a positive functional  satisfying
satisfying

For any ,
,

For any ,
,

And for any ,
,

Thus

Summarying over , we then have, for any
, we then have, for any ,
,

Therefore the frictional market  is weakly arbitrage-free. Q.E.D.
is weakly arbitrage-free. Q.E.D.
[Remark] Theorem 3 means the first fundamental theorem of weakly arbitrage-freeness with frictional security markets. If there exists no transaction costs, that is,  and
and , then Theorem 3 reduces to Theorem 1.
, then Theorem 3 reduces to Theorem 1.
7. Strictly Arbitrage-Free Security Valuation Theorem with Frictional Security Markets
In this section, we assume that  is a separable Banach space. We prove the following Proposition 4 and Theorem 4 for Definition 4’ of the strictly arbitrage-free frictional market
is a separable Banach space. We prove the following Proposition 4 and Theorem 4 for Definition 4’ of the strictly arbitrage-free frictional market .
.
[Proposition ]">4] The frictional market 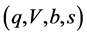 is strictly arbitrage-free if and only if
is strictly arbitrage-free if and only if  and
and  intersect precisely at
intersect precisely at , that is,
, that is, .
.
Proof.  implies that there exists
implies that there exists  such that
such that  and
and . If
. If , then
, then 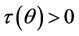 from Definition 4’(1),
from Definition 4’(1),  , which is a contradiction! If
, which is a contradiction! If , then
, then  from Definition 4’(2),
from Definition 4’(2),  and
and . Thus
. Thus and hence
and hence .
.
For sufficiency, we must consider two cases: (1) If there exists  such that
such that 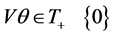 and
and then
then . Take
. Take 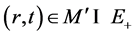 such that
such that  and
and , then
, then which is a contradiction. It follows that any portfolio
which is a contradiction. It follows that any portfolio  of securities has a strictly positive total cost or gain
of securities has a strictly positive total cost or gain  whenever it has a positive payoff
whenever it has a positive payoff . (2) If there exists
. (2) If there exists 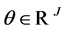 such that
such that  and
and , then
, then . Take
. Take  such that
such that  and
and , then
, then
 , which is a contradiction! The two contradictions mean that the frictional market
, which is a contradiction! The two contradictions mean that the frictional market  is strictly arbitrage-free. Q.E.D.
is strictly arbitrage-free. Q.E.D.
[Remark] The proof of Proposition 4 doesn’t use the representation of the function , then Proposition 4 holds for usual total cost or gain function.
, then Proposition 4 holds for usual total cost or gain function.
[Theorem ]">4] The The frictional market  is strictly arbitrage-free if and only if there exists a strictly positive functional
is strictly arbitrage-free if and only if there exists a strictly positive functional  satisfying
satisfying

Proof. Both  and
and  are closed and convex cones of
are closed and convex cones of  with the vertices at the origin.
with the vertices at the origin.
Since  is a polyhedral (convex) cone in
is a polyhedral (convex) cone in 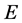 and
and  is a closed convex cone of
is a closed convex cone of ,
,  is a closed convex cone from Lemma of Clark [15], that is,
is a closed convex cone from Lemma of Clark [15], that is, . Thus
. Thus  is a closed convex cone
is a closed convex cone .
.
The frictional market 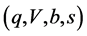 is strictly arbitrage-free if and only if
is strictly arbitrage-free if and only if . We claim that
. We claim that
 .
.
On the contrary, we assume that there exists . Then
. Then 
and  for
for  and
and . Thus
. Thus
 contradicting the fact that
contradicting the fact that  (which follows from
(which follows from  in Proposition 4).
in Proposition 4).
Note that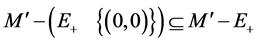 , then
, then
 .
.
Thus, . Since both
. Since both  and
and  are non-empty convex cones with vertices at the origin in the separable Banach space
are non-empty convex cones with vertices at the origin in the separable Banach space , Theorem 5 in Clark [15] states that there exists a non-zero continuous linear functional
, Theorem 5 in Clark [15] states that there exists a non-zero continuous linear functional  on
on 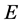 strictly separating
strictly separating  from
from . That is,
. That is,  for all
for all  and
and  for all
for all .
.
The condition  for all
for all  implies that
implies that  is a strictly positive continuous linear functional on
is a strictly positive continuous linear functional on . Thus
. Thus 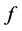 is represented by some
is represented by some  and
and  by
by  for any
for any .
.
The next proof is the same as the corresponding part in Theorem 3. Q.E.D.
[Remark] Theorem 4 means the first fundamental theorem of strict arbitrage-freeness with frictional security markets. If there exists no transaction costs, that is,  and
and , then Theorem 4 reduces to Theorem 2.
, then Theorem 4 reduces to Theorem 2.
8. Concluding Remarks
In Section 4, we examine the following problem: whether the security prices 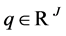 can be represented by strictly positive continuous linear functional
can be represented by strictly positive continuous linear functional  as
as . More precisely, for the security prices
. More precisely, for the security prices  and the returns
and the returns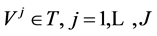 , we study the existence of strictly positive continuous linear functional
, we study the existence of strictly positive continuous linear functional  as
as . Ross [29] and Kreps [18] studied how to extend a linear functional
. Ross [29] and Kreps [18] studied how to extend a linear functional  on
on  to
to  that is strictly positive continuous. However, the existence of the linear functional
that is strictly positive continuous. However, the existence of the linear functional 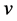 on
on  with
with  is not at all an assured condition. It holds under certain conditions. For example, if
is not at all an assured condition. It holds under certain conditions. For example, if , our result is an analogue of theirs. In the equation
, our result is an analogue of theirs. In the equation , each linear functional
, each linear functional  on
on  corresponds to a vector
corresponds to a vector  and each vector
and each vector  corresponds to a linear functional
corresponds to a linear functional 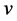 on
on  only if
only if  is column linear independent. Therefore, our results in Section 4 are the same as theirs under the assumption “
is column linear independent. Therefore, our results in Section 4 are the same as theirs under the assumption “ is column linear independent”. But in general, this may not hold.
is column linear independent”. But in general, this may not hold.
Dalang, Morton and Willinger [20] and Jacod and Sgiryaev [22] studied arbitrage-free model, weakly arbitrage-free model, and strongly arbitrage-free model, provided simple proofs of the two fundamental theorems of asset pricing theory. Jacod and Sgiryaev [22] proved that the three concepts are equivalent to each another. In fact, the three concepts are strictly arbitrage-free securities’ price-return pair in Section 2 of our paper. Jacod and Sgiryaev [22] assumed that  is an integrable (finite expectation) random variable (martingale condition). But we only assume
is an integrable (finite expectation) random variable (martingale condition). But we only assume  is in the locally convex topological space
is in the locally convex topological space  for weakly arbitragefree frictionless market (Section 3), and
for weakly arbitragefree frictionless market (Section 3), and  is in the separable Banach space for strictly arbitrage-free frictionless market (Section 4). Therefore our study in Sections 2, 3 and 4 is more general than Jacod and Sgiryaev [22].
is in the separable Banach space for strictly arbitrage-free frictionless market (Section 4). Therefore our study in Sections 2, 3 and 4 is more general than Jacod and Sgiryaev [22].
Pham and Touzi [26] studied frictional markets with the transaction cost rates for purchasing and selling the securities, addressed the problem of characterization of no arbitrage opportunity (strict arbitrage-freeness) in the presence of transaction costs in a discrete-time financial model, and extended the fundamental theorem of asset pricing under a non-degeneracy assumption. We also study the first fundamental valuation theorems of asset pricing from frictionless security markets to frictional security markets in Sections 5, 6 and 7. However, our results are different from those in Pham and Touzi [26] in the following two aspects. (1) The definition of no arbitrage opportunity in Pham and Touzi [26] is different from our definition of strict arbitrage-freeness. (2) Our proofs of Theorems 3 and 4 are different from Pham and Touzi [26]. In fact, we provide the proof by using theory of functional analysis, while Pham and Touzi [26] applied stochastic analysis to prove their results. Therefore, our result works for more general space than theirs.
Frictional economies are fundamentally different from their frictionless counterparts. The theory of general economic equilibrium for frictional economies with incomplete financial markets should be studied. We make the first step by establishing the corresponding no-arbitrage (that is, strictly arbitrage-free) pricing theory. From the first fundamental valuation theorems of asset pricing in general state space with transaction costs we have obtained here, one may further study the corresponding existence of general equilibrium for frictional economy with infinite-dimensional commodity space and incomplete financial markets.
In Section 7, we proved the equivalent conditions (Proposition 4 and Theorem 4) of strictly arbitrage-free frictional market by using Definition 4’. There are some difference between Definitions 4 and 4’. In fact, we can obtain the following (weaker) results for strictly arbitrage-free frictional market as defined by Definition 4.
[Proposition] If the frictional market  is strictly arbitrage-free, then
is strictly arbitrage-free, then  and
and  intersect precisely at
intersect precisely at , that is,
, that is, .
.
[Theorem] If the The frictional market  is strictly arbitrage-free, then there exists a strictly positive functional
is strictly arbitrage-free, then there exists a strictly positive functional  satisfying
satisfying

The proofs of Proposition and Theorem are from the proofs of Proposition 4 and Theorem 4. Conversely, we can’t check the sufficiency. The proof of Theorem 4 holds, too. If
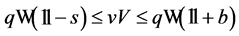
where 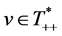 is a strictly positive vector, then, for any
is a strictly positive vector, then, for any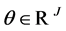 ,
,

then

that is,

If any portfolio  of securities has a zero payoff
of securities has a zero payoff , then it has a positive total cost or gain
, then it has a positive total cost or gain  for the portfolio
for the portfolio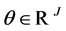 , and a positive total cost or gain
, and a positive total cost or gain  for the portfolio
for the portfolio , thus
, thus

For any portfolio 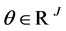 of securities, we can’t obtain a zero total cost or gain
of securities, we can’t obtain a zero total cost or gain  when it has a zero payoff
when it has a zero payoff . That is to say, we can’t make sure that Definition 4 (2) holds. We can’t come to the conclusion that the frictional market
. That is to say, we can’t make sure that Definition 4 (2) holds. We can’t come to the conclusion that the frictional market  is strictly arbitrage-free in the sense of Definition 4.
is strictly arbitrage-free in the sense of Definition 4.
Funding
This work is supported by Social Sciences and Humanities Research Council of Canada (SSHRC Insight Development Grant Number: 430-2012-0698), National Natural Science Foundation of China (NSFC Grant Numbers: 70825003 and 71273271) Major Basic Research Plan of Renmin University of China (Grant Number: 14XNL001)
REFERENCES
- D. Duffie and W. Shafer, “Equilibrium in Incomplete Markets I: A Basic Model of Generic Existence,” Journal of Mathematical Economics, Vol. 14, No. 3, 1985, pp. 285-300. http://dx.doi.org/10.1016/0304-4068(85)90004-7
- D. Duffie and W. Shafer, “Equilibrium in Incomplete Markets II: Generic Existence in Stochastic Economies,” Journal of Mathematical Economics, Vol. 15, No. 3, 1986, pp. 199-216. http://dx.doi.org/10.1016/0304-4068(86)90010-8
- J. Geanakoplos, “An Introduction to General Equilibrium with Incomplete Asset Markets,” Journal of Mathematical Economics, Vol. 19, No. 1-2, 1990, pp. 1-38. http://dx.doi.org/10.1016/0304-4068(90)90034-7
- J. Geanakoplos and W. Shafer, “Solving Systems of Simultaneous Equations in Economics,” Journal of Mathematical Economics, Vol. 19, No. 1-2, 1990, pp. 69-93. http://dx.doi.org/10.1016/0304-4068(90)90036-9
- M. D. Hirsch, M. J. P. Magill and A. Mas-Colell, “A Geometric Approach to a Class of Equilibrium Existence Theorems,” Journal of Mathematical Economics, Vol. 19, No. 1-2, 1990, pp. 95-106. http://dx.doi.org/10.1016/0304-4068(90)90037-A
- S. Y. Husseini, J.-M. Lasry and M. J. P. Magill, “Existence of Equilibrium with Incomplete Asset Markets,” Journal of Mathematical Economics, Vol. 19, No. 1-2, 1990, pp. 39-67. http://dx.doi.org/10.1016/0304-4068(90)90035-8
- M. Magill and W. Shafer, “Incomplete Markets,” In: W. Hildenbrand and H. Sonnenschein, Eds., Handbook of Mathematical Economics (Volume 4), Elsevier Science, North Holland, Amsterdam, 1991, pp. 1523-1614.
- D. Duffie, “Stochastic Equilibria with Incomplete Financial Markets,” Journal of Economic Theory, Vol. 41, No. 2, 1987, pp. 405-416. http://dx.doi.org/10.1016/0022-0531(87)90027-5
- D. Duffie, “Security Markets: Stochastic Models,” Stanford University, Academic Press, Stanford, 1988.
- D. Duffie, “Dynamic Asset Pricing Theory,” Princeton University, Academic Press, Princeton, 1996.
- M. Florenzano and P. Gourdel, “T-period Economies with Incomplete Markets,” Economics Letter, Vol. 44, No. 1-2, 1994, pp. 91-97. http://dx.doi.org/10.1016/0165-1765(93)00308-B
- J. Werner, “Equilibrium of Economies with Incompleete Financial Markets,” Journal of Economic Theory, Vol. 36, No. 1, 1985, pp. 110-119. http://dx.doi.org/10.1016/0022-0531(85)90081-X
- J. Werner, “Structure of Financial Markets and Real Indeterminacy of Equilibrium,” Journal of Mathematical Economics, Vol. 19, No. 1-2, 1990, pp. 217-232. http://dx.doi.org/10.1016/0304-4068(90)90043-9
- S. Zhang, “Existence of Stochastic Equilibrium with Incomplete Financial Markets,” Applied Mathematics—Journal of Chinese Universities, Vol. 13, No. 1, 1998, pp. 77-94.
- S. A. Clark, “The Valuation Problem in Arbitrage Pricing Theory,” Journal of Mathematical Economics, Vol. 22, No. 5, 1993, pp. 463-478. http://dx.doi.org/10.1016/0304-4068(93)90037-L
- S. A. Clark, “Vector Space Methods in Additive Theory,” Journal of Mathematical Economics, conditionally accepted, 1994.
- J. M. Harrison and D. M. Kreps, “Martingales and Arbitrage in Multiperiod Securities Markets,” Journal of Economic Theory, Vol. 20, No. 3, 1979, pp. 381-408. http://dx.doi.org/10.1016/0022-0531(79)90043-7
- D. M. Kreps, “Arbitrage and Equilibrium in Economies with Infinitely Many Commodities,” Journal of Mathematical Economics, Vol. 8, No. 1, 1981, pp. 15-35. http://dx.doi.org/10.1016/0304-4068(81)90010-0
- J. M. Harrison and S. R. Pliska, “Martingales and Stochastic Integrals in the Theory of Continuous Trading,” Stochastic Processes and Their Applications, Vol. 11, No. 3, 1981, pp. 215-260. http://dx.doi.org/10.1016/0304-4149(81)90026-0
- R. C. Dalang, A. Morton and W. Willinger, “Equivalent Martingale Measures and No-Arbitrage in Stochastic Securities Market Models,” Stochastics and Stochastic Reports, Vol. 29, No. 2, 1990, pp. 185-201. http://dx.doi.org/10.1080/17442509008833613
- K. Back and S. R. Pliska, “On the Fundamental Theorem of Asset Pricing with an Infinite State Space,” Journal of Mathematical Economics, Vol. 20, No. 1, 1991, pp. 1-18. http://dx.doi.org/10.1016/0304-4068(91)90014-K
- J. Jacod and A. N. Sgiryaev, “Local Martingales and the Fundamental Asset Pricing Theorems in the Discrete-Time Case,” Finance and Stochastics, Vol. 2, No. 3, 1998, pp. 259-273. http://dx.doi.org/10.1007/s007800050040
- Z. Chen, “Financial Innovation and Arbitrage Pricing in Frictional Economics,” Journal of Economic Theory, Vol. 65, No. 1, 1995, pp. 117-135. http://dx.doi.org/10.1006/jeth.1995.1004
- E. Jouini and H. Kallal, “Martingales and Arbitrage in Securities Markets with Transaction Costs,” Journal of Economic Theory, Vol. 66, No. 1, 1995, pp. 178-197. http://dx.doi.org/10.1006/jeth.1995.1037
- E. Jouini and H. Kallal, “Arbitrage in Securities Markets with Short-Sales Constraints,” Mathematical Finance, Vol. 5, No. 3, 1995, pp. 197-232. http://dx.doi.org/10.1111/j.1467-9965.1995.tb00065.x
- H. Pham and N. Touzi, “The Fundamental Theorem of Asset Pricing with Cone Constraints,” Journal of Mathematical Economics, Vol. 31, No. 2, 1999, pp. 265-279. http://dx.doi.org/10.1016/S0304-4068(97)00059-1
- J. Farkas, “Uber die Theorie der Einfachen Ungleichungen,” Journal für die Reine und Angewandte Mathematik, Vol. 1902, No. 124, 1902, pp. 1-24.
- J. Franklin, “Methods of Mathematical Economics,” Springer-Verlag, New York, 1980.
- S. A. Ross, “A Simple Approach to the Valuation of Risky Streams,” Journal of Business, Vol. 51, No. 3, 1978, pp. 453-475. http://dx.doi.org/10.1086/296008
NOTES

*Corresponding author.

