Journal of Mathematical Finance
Vol.2 No.2(2012), Article ID:19219,3 pages DOI:10.4236/jmf.2012.22022
Generalized Stochastic Processes: The Portfolio Model
University of the West Indies, St. Augustine, Trinidad and Tobago
Email: malghalith@gmail.com
Received March 1, 2012; revised April 3, 2012; accepted April 15, 2012
Keywords: stochastic process; investment; portfolio
ABSTRACT
Using the portfolio model, we introduce a general stochastic process that is not necessarily a diffusion/jump process and the random variable is not necessarily normally distributed.
1. Introduction
The literature on stochastic processes (especially in finance) relied mainly on Levy processes such as Wiener process, Poisson process, and the Variance-Gamma process. Examples include Madan and Seneta [1], Focardo and Fabozzi [2], among many others. Much of the literature assumes a Wiener process (Brownian motion), which implies normally distributed and independent stationary increments. The Brownian motion is extensively used in stochastic finance especially in investment models (see, for example, Alghalith [3]).
However, these assumptions of diffusion/jump process and Gaussian/Poisson distribution (or any specific probability distribution) can be relaxed. That is, we can introduce a general stochastic process that is more general than the Levy process without losing significant analytical convenience. Consequently, this paper offers three major contributions. First, it relaxes the assumption of a diffusion/jump process. Secondly, it relaxes the Gaussian/Poisson distribution or any specific probability distribution. Thirdly, it provides solutions without reliance on the existing duality or variational methods. Moreover, we introduce a general model that can be applied to any specific topic.
2. The Model
In general, a continuous stochastic process 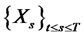
can be written as a function of a control variable, state variables and a random variable as the following (the first two integrals can be zero)
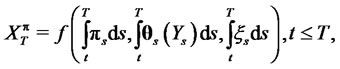 (1)
(1)
where 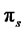 is the control variable,
is the control variable, 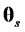 is a vector of state variables or coefficients,
is a vector of state variables or coefficients, 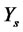 is a stochastic factor, and
is a stochastic factor, and  is a random variable (not necessarily a Brownian motion) and thus the assumption of normal distribution (or any specific probability distribution) is not required. Moreover, in contrast to Levy processes,
is a random variable (not necessarily a Brownian motion) and thus the assumption of normal distribution (or any specific probability distribution) is not required. Moreover, in contrast to Levy processes,  is not necessarily a linear (diffusion) function. In addition, we assume
is not necessarily a linear (diffusion) function. In addition, we assume  is admissible and progressively measurablewhere
is admissible and progressively measurablewhere 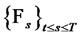 is the filtration.
is the filtration.
The objective is to maximize the expected utility of  with respect to
with respect to 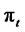

where 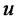 is a differentiable, bounded and concave utility function. Using the method of Alghalith [4], the solution yields
is a differentiable, bounded and concave utility function. Using the method of Alghalith [4], the solution yields
 (2)
(2)
where the subscript denote the derivatives.
Consider this exact Taylor polynomial (and suppressing the notations) (Equation (3))
Taking expectations of both sides yields (Equation (4))
|
|
Thus,
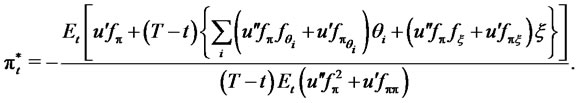 (5)
(5)
3. Example—The Investment/Consumption Model
It is well-known that the stock price  is a function of the expected return
is a function of the expected return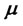 , the volatility
, the volatility 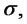 and a random variable
and a random variable 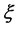
 (6)
(6)
where  is stochastic economic factor. However,
is stochastic economic factor. However, 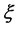
is not necessarily normally distributed and 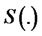 is not necessarily a linear function. Consequently, the wealth function is given by
is not necessarily a linear function. Consequently, the wealth function is given by
 (7)
(7)
where 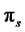 is the portfolio process,
is the portfolio process, 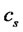 is the consumption process,
is the consumption process, 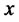 is the initial wealth,
is the initial wealth, 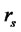 is the risk-free rate of return. Thus,
is the risk-free rate of return. Thus,
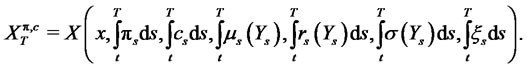 (8)
(8)
The objective is to maximize the expected utility of wealth and consumption with respect to the portfolio and consumption
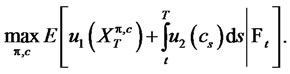
The solutions are
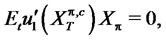 (9)
(9)
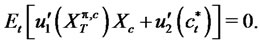 (10)
(10)
Using an exact Taylor expansion (and suppressing the notations), we obtain
 (11)
(11)
Thus,
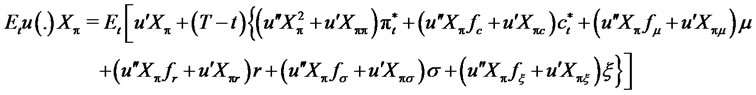 (12)
(12)
Therefore we can obtain expressions for the optimal portfolio and consumption
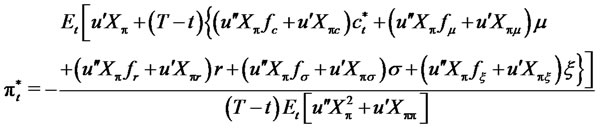 (13)
(13)
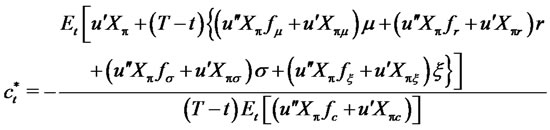 (14)
(14)
We can obtain explicit solutions under specific forms of the utility function. For example, under mean-variance (quadratic) preference, we can obtain explicit solutions since 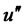 is constant and
is constant and  is linear. It is worth noting that even with Levy process general explicit solutions were not provided by the literature; thus, the assumption of a Levy process does not offer a significant analytical convenience.
is linear. It is worth noting that even with Levy process general explicit solutions were not provided by the literature; thus, the assumption of a Levy process does not offer a significant analytical convenience.
REFERENCES
- D. Madan and E. Seneta, “The Variance-Gamma (V-G) Model for Share Market Returns,” Journal of Business, Vol. 63, No. 4, 1990, pp. 511-524. doi:10.1086/296519
- F. Focardi and F. Fabozzi, “The Mathematics of Financial Modeling and Investment Management,” Wiley E-Series, 2004.
- M. Alghalith, “A New Stochastic Factor Model: General Explicit Solutions,” Applied Mathematics Letters, Vol. 22, No. 12, 2009, pp. 1852-1854. doi:10.1016/j.aml.2009.07.011
- M. Alghalith, “An Alternative Method of Stochastic Optimization: The Portfolio Model,” Applied Mathematics, Vol. 2, No. 7, 2011, pp. 912-913. doi:10.4236/am.2011.27123



