Open Journal of Obstetrics and Gynecology
Vol.07 No.03(2017), Article ID:74860,17 pages
10.4236/ojog.2017.73035
Automatic Detection and Measurement of Fetal Biparietal Diameter and Femur Length ―Feasibility on a Portable Ultrasound Device
Naiad Hossain Khan1*, Eva Tegnander2,3, Johan Morten Dreier2, Sturla Eik-Nes2,3, Hans Torp1, Gabriel Kiss1
1Department of Circulation and Medical Imaging (ISB, MI Lab), Norwegian University of Science and Technology, Trondheim, Norway
2National Center for Fetal Medicine, St. Olavs Hospital, Trondheim, Norway
3Department of Laboratory Medicine, Children’s and Women’s Health, Norwegian University of Science and Technology, Trondheim, Norway

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 27, 2017; Accepted: March 20, 2017; Published: March 23, 2017
ABSTRACT
An automatic method able to recognize a presented section through the biparietal plane of the fetal head and a section through the fetal femur in ultrasound images is developed. Once the correct anatomical section for measurement is identified by the machine, the placement of the measurement calipers is automatically determined by fitting an active contour model to the structure of interest. The fetal biparietal diameter (BPD) and femur length (FL) are then measured automatically. The validation data set contained 167 and 197 B- mode images for BPD and FL measurements, respectively. The images were acquired using 4 different ultrasound scanners, which resulted in varied image quality and gain settings. The mean gestational age (GA) of the fetuses was 19.4 weeks, range 16 to 41 weeks. A measurement success rate of 90% was achieved for both BPD and FL. The correlation coefficients between the manual and automatic measurements were 0.995 (BPD) and 0.967 (FL), mean errors were 0.5 mm (BPD) and -1.7 mm (FL) and error range with 95% confidence interval (CI) were −3.8 - 4.8 mm (BPD) and −11.4 - 8.1 mm (FL). The automatic measurement results were consistent in both high and low gain settings. The intraclass correlation coefficients between manual and automatic measurements were 0.995 (95% CI; 0.981 - 0.999) for BPD in high gain, 1.0 (95% CI; 0.998 - 1.0) for BPD in low gain, 0.998 (95% CI; 0.991 - 0.999) for FL in high gain and 0.999 (95% CI; 0.996 - 1.0) for FL in low gain settings. The method was implemented on a prototype, portable ultrasound machine designed to be used in low- and middle-income countries (LMIC). The overall performance of the method supports our hypothesis that automated methods can be used and are beneficial in a clinical setting.
Keywords:
Fetal Dating, Biparietal Diameter, Femur Length, Portable Ultrasound Machine, Automatic Measurement

1. Introduction
Ultrasound scanning in pregnancy has become the standard for care in the high income countries (HIC) [1] . It is currently offered at week 12 or around week 18, or both. The general purpose of the ultrasound examination is to determine the location of the fetus and the placenta, the number of fetuses, the gestational age (GA) and estimated day of delivery (EDD) and to detect anomalies as a basis for further fetal medical management [2] .
The benefit of using ultrasound to improve pregnancy care is equally important in low- and middle-income countries (LMIC) as in the HIC. In LMIC, insufficient dating, high rate of fetal growth restriction, insufficient detections of twins before birth are common factors. However, the use of ultrasound in LMIC is not as widespread as in the HIC for a number of reasons. Much of the ultrasound equipment developed for use in HIC is too sensitive to be used in the rough environments of LMIC. Due to varying sources of current, large variations in temperature and humidity, transport, shock and vibration, and dusty environments, essential parts break and cannot be replaced or repaired. Another major problem is the high cost of ultrasound machines. Moreover, in the rural areas of LMIC, there is a lack of technical knowledge for operating ultrasound machines.
Our research group is currently developing a prototype of an affordable, portable and user-friendly ultrasound machine (the Umoja scanner) based on a tablet device (Figure 1). In order to lower the usability threshold of the device, we are in the process of automating as many of the manual measurement procedures as possible [3] [4] and implement them on the portable machine. It is our hypothesis that automated measurement methods combined with a minimal user interface (UI) (Figure 1(b)) will facilitate the adoption of ultrasound in LMIC. With this UI, the functions found in a conventional ultrasound machine are carried out by simple touch interactions. For instance: the scan depth is adjusted
Figure 1. The Umoja prototype scanner. (a) Measurement of the biparietal diameter (BPD). (b) Screen capture of the user interface for BPD measurement.
by a pinch-zoom gesture on the screen; the cine loop function is performed by sliding the finger on the screen from left to right; the position of the measurement calipers can be easily adjusted by a drag gesture. Extra functions (e.g. creating a new patient record, reviewing patient data etc.) are accessed by using the side buttons. The desired end result is a robust, cheap ultrasound machine with an adequate image quality that may be operated in LMIC by personnel with limited technical knowledge and understanding.
The assessment of GA is important and often missing in LMIC. GA is used to predict EDD, track fetal growth and refine clinical management in connection with premature delivery and around term [5] . For calculating GA and subsequently the EDD, the biparietal diameter (BPD) and/or the fetal femur length (FL) are the most commonly used and well documented parameters [6] [7] [8] .
Typically, both BPD and FL are measured manually by ultrasound trained midwives, sonographers, radiographers or doctors. The fetal dating process requires the localization of an ultrasound scan plane containing given anatomic landmarks and placement of measurement markers. The measurements are prone to both intra- and inter-observer variability [9] . In order to reduce these errors, the measurement process is repeated a number of times (typically three) and either the mean or the maximum value of these measurements is recorded. Correct adjustment of the image gain settings is necessary to obtain comparable results for a population or community. If the gain is set too high or too low, it would significantly affect the BPD and FL measurement and thus the calculated GA.
Several methods [10] - [16] ―ranging from semi-automatic to fully automatic―for improving the accuracy of BPD and FL measurements and for simplifying the fetal dating process have been published in the literature. However, none of these methods was aimed for use on portable ultrasound machines.
The aim of this study was to develop and validate an automatic method to recognize a presented scan plane through the fetal head and femur and then measure the BPD and FL. The method was designed to run on an off-the-shelf tablet device with limited computational power and therefore it can be easily integrated with a portable ultrasound machine. A further aim was to make the method adapt to varying gain settings.
2. Materials and Methods
A total of 273 images suitable for BPD measurement and 321 images suitable for FL measurement were randomly obtained from a local archive of B-mode ultrasound images. For development purposes, 106 BPD and 124 FL images were randomly selected and stratified according to the gestational age. The remaining 167 BPD and 197 FL images were used for validation. The images were acquired during routine ultrasound examinations performed by formally ultrasound trained midwives at the National Center for Fetal Medicine, St. Olavs University Hospital at the Norwegian University of Science and Technology. Informed consent for additional electronic processing was obtained from the women prior to the examinations. The Regional Ethics Committee approved the research project (2016/795 and 2016/1173). The mean GA ± standard deviation (SD) of the fetuses was 19.4 ± 6.7 weeks, range between 16 to 41 weeks. The following ultrasound machines: Voluson E6 (GE Medical Systems, Zipf, Austria), Voluson E8 (GE Medical Systems, Zipf, Austria), Voluson 730 (GE Medical Systems, Zipf, Austria), Vivid q (GE Medical Systems, Tirat Carmel, Israel), Acuson Antares Premium Edition (Siemens Medical Solutions, Mountain View, CA, USA), and HI VISION Preirus EUB-8500 (Hitachi Medical Corporation, Tokyo, Japan) were used for acquisition purposes.
On the collected images, both BPD and FL were measured manually by the fully ultrasound trained midwives, following current guidelines. These measurements were considered as the reference; the descriptive statistics of the image data set are presented in Table 1. The BPD was measured according to two accepted conventions: the BPD outer-outer and the BPD outer-inner measurement techniques [17] . In the first case, BPD was measured by calculating the distance between the outer boundaries of the parietal bones perpendicular to the falx cerebri on the plane through the cavum septi pellucidi [6] . In the second case, the distance was measured on the same plane from the outer edge of the upper boundary to the inner edge of the bottom boundary of the fetal skull. The FL was calculated by measuring the length of a straight line passing through the ossified portion of the femoral diaphysis connecting the endpoints of a femur [8] .
MATLAB version R2013a (The MathWorks Inc., Natick, MA, USA) was used to calculate statistical measurements such as: correlation coefficient, mean error, error range with confidence interval (CI) and SD to compare the measurements of the developed automatic method with their corresponding reference measurements. In addition, SPSS Statistics version 24 (IBM Corp. Armonk, NY, USA) was used to calculate intraclass correlation coefficient (ICC) to verify the reliability and consistency of the measurements produced by the manual and automatic methods.
2.1. Technical Description
The automatic BPD and FL measurement method was developed by leveraging
Table 1. Descriptive statistics of the image data set based on manual measurements performed by formally ultrasound trained midwives.
SD = Standard deviation; a. Outer-outer measurement; b. Outer-inner measurement.
the open source computer vision (OpenCV) version 2.4.9 library (Itseez, San Francisco, CA, USA) (http://opencv.org) and the real-time contour tracking library (RCTL) (GE Vingmed Ultrasound, Horten, Norway) [18] . The OpenCV is an open-source, cross-platform solution for applying different types of image processing techniques. The RCTL is a closed-source, cross-platform commercial library which is capable of fitting a deformable active contour model to a structure of interest in a B-mode ultrasound image.
The automatic method measured BPD and FL in three steps (Figure 2). First, OpenCV routines were used to pre-process an image and detect the fetal skull or femur. Second, RCTL was used to fit a deformable active contour model along the boundary of the detected skull or femur. Finally, a straight line was calculated inside the converged active contour model and its endpoints were adjusted to measure BPD or FL using the OpenCV library. The detailed descriptions of these steps are presented in the following subsections.
2.2. Step 1a: Fetal Skull Detection
To detect the fetal skull, a region of interest (ROI) was automatically selected
Figure 2. The steps of the developed automatic method for BPD and FL detection and measurement.
from the upper-middle part of a B-mode image where the ultrasound echo is generally strong (Figure 3(a)). The height and width of the ROI are equal to half of the height and width of the B-mode image. The mean value and SD of the pixel intensities were calculated from the ROI to estimate the overall intensity level of the image. Gaussian smoothing was performed by a 3-by-3 kernel to remove noise from the image. At this stage, the Canny edge detection algorithm [19] was used to identify the edges in the B-mode image. The upper threshold of the algorithm was set to 1.33 * mean intensity, and the lower threshold was set to the half of the upper threshold. The Cartesian coordinates of the edge pixels were recorded after the edges were detected. The image gradient was calculated using the first-order Sobel derivative [20] along the X and Y axes. The direction of the gradient pointed to the direction of intensity level change in the image, and was perpendicular to any local edge.
Next, the circle Hough transform (CHT) [21] was used to detect the bright circular fetal skull. The algorithm of CHT is explained in Figure 3(b) & Figure 3(c) [22] . An edge pixel (the black circle in Figure 3(b)) was assumed on the boundary of the circular fetal skull (the white circle in Figure 3(b)) and its local gradient vector direction were considered. A new list of pixels ― which were
Figure 3. The fetal skull detection process. (a) A region of interest (ROI) located at the upper-middle part of a B-mode image was automatically selected for image intensity estimation. (b) An edge pixel (the black circle) was assumed to be situated on the periphery of a fetal skull (the white circle on the gray background). Its local gradient direction is shown by the arrow and the number of votes in the circle Hough transform (CHT) accumulator are shown for each of the pixels situated along the gradient direction. (c) Number of votes gradually increased for the center pixel. (d) The result of CHT which is used to initialize the active contour shown by the white circle.
situated along the local gradient vector direction of the considered edge pixel―was registered in the 2D Hough accumulator. These new pixels were located within a 9.5 to 55 mm radii range to measure any BPD between 37.6 to 103 mm corresponding to a 16 to 41-week-old fetus. Each of the new pixels received a vote from the edge pixel for being located along its gradient vector direction. The number of votes for the pixel at the center increased gradually as more edge pixels were considered, as illustrated in Figure 3(c). The pixels were sorted in descending order by the number of their votes and the one with the highest number of votes in the accumulator was selected as the center of a potential circle (the white circle in Figure 3(d)) that circumscribed the fetal skull. The radius of the circle was selected by choosing the best supported distance between the selected center and all the edge pixels recorded earlier.
2.3. Step 1b: Fetal Femur Detection
A B-mode image with a fetal femur often contained the ultrasound echo originating from the subcutaneous fat and the skin of the fetal leg (Figure 4(a)). To detect the fetal femur, the mean and SD of the intensity of a B-mode image were calculated in the same way as described for the BPD. The sum of the mean intensity and SD was selected as a threshold for binary thresholding. A list of contours was prepared from the edges between the black and the white regions in the binary image (Figure 4(b)). Four different parameters: width, aspect ratio, centroid, and orientation were calculated for each of these contours. A contour was kept in the list when three criteria were satisfied. First, the contour’s width should be within 19 to 93 mm to measure any FL between 19.4 to 82 mm corresponding to a 16 to 41-week-old fetus. Second, the contour’s aspect ratio should be higher than 3.5, denoting an elongated structure resembling a femur. Third, the contour should not be adjacent to the top or the bottom boundary of the image. This was checked against the position of the contour’s centroid.
Next, the contours were sorted in descending order by their widths. The widest contour from the list was selected as the potential femur candidate. The ultrasound echo originating from the skin of the fetal leg often appears as a bright, parallel line above the femur. Therefore, the orientation and width of the femur candidate were compared with those of the second widest contour in the list. The second widest contour was chosen as the new femur candidate if it was located close below the old femur candidate and had similar width (width ratio more than 0.60) and orientation (difference in orientation less than 15 degrees). In this case, the old femur candidate was discarded since it most likely represented the skin above the femur.
The progressive probabilistic Hough transform (PPHT) [23] [24] was used at the location of the femur candidate in the binary image to find a straight line that passed through the ossified portion of the femur. The following polar equation of line was used:
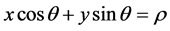 (1)
(1)
where ρ represents the shortest distance between the origin and a line, and θ represents the angle between the line and x-axis (Figure 4(c)). For every pixel in the femur candidate, a sinusoid was generated in ρ − θ plane by using the pixel’s Cartesian coordinates (i.e. x and y) as parameters and ρ and θ as variables in Equation (1) (Figure 4(d)). The sinusoid represented the ρ and θ of all the lines which could pass through that particular pixel. Multiple sinusoids were generated for all the pixels of the femur candidate (Figure 4(e)). Two sinusoids overlapped each other if they were generated from two pixels situated on the same line. The ρ and θ of this line corresponded to the ρ and θ of the cell where the overlap took place. Each of the cells in ρ − θ plane received a vote in the Hough accumulator when a sinusoid passed through it. The cell that had the highest number of votes or many sinusoid overlaps was considered as a peak (shown by the green square in Figure 4(e)). In PPHT, which is a variant of Hough transform, it was assumed that if a peak in the Hough accumulator plane was going to be high, then accumulating votes of that particular cell for a limited number of times would be enough to identify a straight line inside the ossified portion of the femur as shown in Figure 4(f) [22] .
2.4. Step 2: Active Contour Model Adjustment
After the fetal skull or the femur was detected, a deformable active contour model was initialized and subsequently fitted to the image by using RCTL. The approach proposed by Orderud (2010) was employed, in which a Kalman-based tracker was used. The measurement vector for the Kalman filter was a set of edge detectors perpendicular to the model and equally spread along the contour,
Figure 4. Fetal femur detection process. (a) A B-mode ultrasound image showing a fetal femur, the skin of the leg, and the echo from subcutaneous fat from the mother. (b) A list of detected contours. (c) A line is represented by ρ and θ in polar form. (d) Any pixel of the femur candidate represented a sinusoid in ρ − θ plane. (e) Multiple pixels on the same line inside the femur candidate represented multiple overlapping sinusoids in ρ − θ plane. The green square shows the cell with the highest number of votes. (f) The result of the progressive probabilistic Hough transform (PPHT) shown by a white straight line inside the fetal femur.
whereas the state vector consists of a set of control points defining the shape of a non-uniform rational basis spline (NURBS) curve depicting the skull or the femur. The following equations give the measurement update of the Kalman tracker:
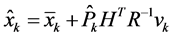 (2)
(2)
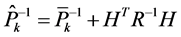 (3)
(3)
with 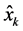 the updated state estimate, H includes the edge measurements, R represents the measurement covariance matrix, P̂ the updated error covariance matrix and
the updated state estimate, H includes the edge measurements, R represents the measurement covariance matrix, P̂ the updated error covariance matrix and 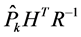 the Kalman gain that assimilates the edge related measurements. The cubic NURBS model had 12 control points and 75 edge detection locations. A step edge detector gave the most reliable results and therefore was chosen for all measurements. The anatomic landmarks of interest for the skull and femur were defined in the NURBS’ parametric space thus ensuring that the same location along the curve for all images is extracted for measurement.
the Kalman gain that assimilates the edge related measurements. The cubic NURBS model had 12 control points and 75 edge detection locations. A step edge detector gave the most reliable results and therefore was chosen for all measurements. The anatomic landmarks of interest for the skull and femur were defined in the NURBS’ parametric space thus ensuring that the same location along the curve for all images is extracted for measurement.
In the case of the fetal skull, an elliptic model was placed at the center of the circle circumscribing the fetal skull (Figure 5(a)). The semi-major axis of the ellipse was set to 0.8 of the radius of the circumscribing circle. After 4 iterations, the model was assumed to be in its converged state along the boundary of the fetal skull (Figure 5(b)).
In the case of the femur, the deformable model was initialized at the center of the identified straight line found by PPHT and oriented according to the orientation of the femur candidate (Figure 5(c)). After 10 iterations, the model was considered to be in a converged state (Figure 5(d)).
Figure 5. The initial and converged active contour models. (a) Initialization of the model inside the fetal skull. (b) Converged state along the fetal skull boundary after 4 iterations. (c) Initial state of the deformable model for the fetal femur. (d) Converged state along the fetal femur boundary after 10 automatic iterations.
2.5. Step 3: BPD and FL Computation
The top and the bottom endpoints of the minor axis of the converged elliptical model in the fetal skull were located on the parietal bones. These were defined in parametric coordinates along the deformable model such that they corresponded to the maximum edge location. The gray values of the pixels both above and below these endpoints were analyzed to identify the inner and outer edges of the parietal bone by adaptive binary thresholding using the OpenCV library (Figure 6). The binary threshold value was selected by taking the summation of the mean intensity and 2 × SD of the image intensity estimated from the ROI. Finally, the distance between the outer edge of the parietal bone at the top of the minor axis and the inner edge of the parietal bone at the bottom of the minor axis was calculated as BPD outer-inner. The distance from the outer edge of the parietal bone at the top of the minor axis to the outer edge of the parietal bone at the bottom of the minor axis was calculated as BPD outer-outer measurement.
Likewise, a straight line corresponding to the widest distance was identified inside the converged model of the fetal femur. The endpoints of the line were located close to the boundary of the femur. The positions of these endpoints were also adjusted to calculate accurate FL.
3. Results
The automatic method was able to measure BPD in 147 of 167 images (88%) and
Figure 6. Detection of inner and outer edge points of the fetal skull boundary by analyzing pixel gray values. (a) A B-mode image displaying a converged elliptical model for a fetal skull. The green straight line represents the minor axis of the ellipse. A region of interest (ROI) near the skull boundary is shown by the red box. (b) The enhanced view of the ROI. The red point represents the lower end of the minor axis of the ellipse. The cyan and yellow points represent the inner and outer edge points of the skull boundary respectively. The white straight line represents 10 mm vertical distance along the red point. (c) The pixel gray value profile along the 10 mm white straight line. Adaptive binary thresholding (value = 78) was performed on these gray values to detect the indices of the inner (cyan point) and outer (yellow point) edge points of the fetal skull boundary.
FL in 181 of 197 images (92%) in the validation set. Table 2 presents the success rates of the automatic method for the different ultrasound scanners used for the acquisition of the images belonging to the validation set. The correlation plots and the error versus reference plots between the manual and automatic BPD and FL measurements are shown in Figure 7.
Table 3 presents the correlation coefficient (r), regression line, mean error, and the error range with 95% CI in millimeter and percentage scales for the automatic BPD outer-outer and outer-inner measurements, and for the FL measurements.
To check for intra- and inter-observer variability, the manual and automatic BPD and FL measurements based on 10 randomly selected images in 3 separate trials were computed. The ICC for the manual measurements in the 3 trials was 0.999 (95% CI; 0.997 - 1.0) and for automatic measurements was 1.0. The ICC between the average of the manual measurements and automatic measurements was 0.999 (95% CI; 0.996 - 1.0). The mean bias ± SD of the automatic measurement was −0.4 ± 0.5 mm.
To show that the method works equally well for various gain settings, 20 B-mode images were selected for BPD measurement―10 with high gain and 10 with relatively low gain. The same procedure was performed on 20 B-mode images of the femur―10 with high gain and 10 with relatively low gain settings. The mean gray value ± SD of the images with high gain were 87 ± 16 (BPD) and 60 ± 16 (FL). For the images with low gain, these values were 24 ± 8 (BPD) and
Figure 7. Correlation and error plots between automatic and manual BPD and FL measurements. Correlation coefficient (r), regression line equation, mean error with 95% confidence interval are shown in the plots.
12 ± 5 (FL). For the BPD images with high gain, the ICC between manual and automatic measurements was 0.995 (95% CI; 0.981 - 0.999), and for the BPD images with low gain, the ICC was 1.0 (95% CI; 0.998 - 1.0). For FL images with high gain, the ICC was 0.998 (95% CI; 0.991 - 0.999), and for the FL images with low gain, the ICC was 0.999 (95% CI; 0.996 - 1.0).
Finally, the method was implemented in the Umoja scanner prototype which used a Samsung P600 tablet (Samsung Electronics, Suwon, South Korea) to visualize the ultrasound data streamed from a Vivid q portable ultrasound machine (GE Medical Systems, Tirat Carmel, Israel). The mean execution time ± SD for all validation images was: 1.3 ± 0.3 s (BPD) and 1.6 ± 0.4 s (FL) on a Nexus 5X mobile device (LG Electronics, Seoul, South Korea), 1.2 ± 0.4 s (BPD) and 2.2 ± 0.9 s (FL) on a Nexus 10 tablet device (Samsung Electronics, Suwon, South Korea), and 1.2 ± 0.4 s (BPD) and 1.9 ± 0.7 s (FL) on a Samsung P600 tablet device (Samsung Electronics, Suwon, South Korea).
4. Discussion
This feasibility study showed that it was possible to develop an automatic measurement technique of essential fetal parameters and implement it on an off-the-shelf tablet device. The obtained detection and accuracy rates are comparable to other published automatic state of the art methods, which may be run on high end ultrasound machines, only. The success rate of fetal skull and femur localization did not vary significantly when using different ultrasound machines (Table 2). The correlation coefficients presented in Table 3 are close to 1, which shows a strong linear relationship between the manual and automatic BPD and FL measurements (Figure 7).
Table 2. The success rates of the automatic method for the scanners used in the validation set.
Table 3. Comparison between manual and automatic BPD and FL measurements for the validation set.
r = correlation coefficient; CI = confidence interval; aOuter-outer measurement; bOuter-inner measurement.
The development of our technique required as input ultrasound images that were suitable for BPD or FL measurement. In the context of this study, these images were obtained from the local database at our medical center. Therefore, our results need a validation of the proposed methods in LMIC; this is the object of on-going work.
The mean error and the error range found between the manual and automatic measurements are comparable with the inter-observer variability documented on high end ultrasound machine by Perni et al. [9] . Their inter-observer variability was based on 122 images from singleton pregnancies acquired with Acuson 128 XP (Acuson Inc., Mountain View, CA, USA). An ICC value of 1 for intra-observer variability shows that our automatic method achieves consistent results; furthermore, a high ICC between the manual and automatic measurements is indicative of the fact that our method correlates very well with manual measurements.
The detection rate of the oval fetal skull plane and the femur was approximately 90% in both cases. In the case of the BPD measurement, the method failed when other circular edges or flat shaped parietal bones were present (Fig- ure 8(a) & Figure 8(b)). The FL measurement typically failed when the femur
Figure 8. Detection failures. (a) A B-mode image with fetal skull. (b) BPD measurement failed due to relatively flat parietal bones of the skull. (c) A B-mode image with fetal femur. (d) FL measurement failed because of inseparable femur from other object in binary image. (e) Overestimation of FL by the automatic method shown by red circular measurement calipers. (f) Manual correction by the user.
was inseparable from other objects in the binary image, as shown in Figure 8(c) & Figure 8(d). An underestimation bias was present in the automatic FL measurements due to the presence of shadows and inhomogeneous brightness for femurs of older fetuses. In the case of unsuccessful detection or measurement failure, the user can, by dragging, easily adjust the BPD or FL measurement line proposed by the automatic method during the measurement acceptance step of the protocol as illustrated in Figure 8(e) & Figure 8(f).
As seen in Table 4, the results of our automatic method (see Table 3) are comparable to those of the other automatic methods [10] - [16] . All of these methods are PC-based, whereas our method achieved similar results within the limited hardware settings available on portable devices.
To ensure the robustness of the automatic method, the ultrasound images were derived from different ultrasound machines with varying image quality. The method’s parameters were automatically adjusted according to the image gain setting which was estimated from the upper-middle ROI in the ultrasound image. Strong ICC between manual and automatic measurements from the images with high and low gain showed that the method successfully localized and measured the fetal skull and femur on images with different gain settings. A uniform setting of the gain is a prerequisite for uniform measurement between examiners. This may be achieved by experienced examiners in different centers [5] [25] [26] . However, for beginners with limited experience of technology such as in LMIC, various levels of gain may result in incorrect measurements, thus affecting the various predictions of GA and fetal growth deviation.
The combined approach of using CHT, PPHT, and RCTL overcame some of the common problems in automatic measurements such as: incomplete fetal skull contour, high curvature in femur and, in some cases, the intensity variation
Table 4. Performance comparison between existing automatic BPD and FL measurements techniques and the developed automatic method.
r = correlation coefficient; CI = confidence interval; aSemi-automatic method; bDerived from the available data.
within femur. Unlike the database-based segmentation approach [10] , our method did not require any large training data set to train a classifier.
The method was tested on a mobile phone (Nexus 5X), and low (Nexus 10) and high-performance (Samsung P600) tablet devices. The mean execution time and SD show that the automatic method was capable of performing quickly on devices available on the market. The FL measurement process required a longer time to complete because of the additional investigations that were needed to differentiate the actual fetal femur from other similarly shaped artefacts such as the fetal leg skin and echo from subcutaneous fat. It was possible to implement this cross-platform automatic method in PCs and on portable devices with few modifications because it used the Open CV and RCTL, which are cross-platform libraries. Consequently, the popular fetal measurement tables used worldwide may easily be implemented to work with the presented automatic method for automatic measurement of fetal BPD and FL to derive GA and EDD of a fetus [17] [27] [28] and one is already available on the tablet device [7] [29] . We chose to report BPD and FL values as they are independent of the dating formula.
5. Conclusion
An automatic measurement technique for use in obstetrics has been developed and implemented on an off-the-shelf tablet device. The automatically measured BPD and FL values were comparable to the manual measurements. The performance and accuracy of the results are similar to those of other state of the art automatic methods, which may be run only on high end ultrasound machines. Through its integration into an affordable and easy to use ultrasound machine such as the Umoja scanner, the method has the potential for clinical usability in LMIC. Furthermore, the automatic measurement technique is adaptive to the image gain settings. This is a feature which will facilitate the achievement of uniform results of measurements among users in a low technological setting found in LMIC, and thus will contribute to both increased quality of measurements and ease of use.
Acknowledgements
The research was funded by the project ‘Umoja―ultrasound for midwives in rural areas’ Helse Midt-Norge RHF. The text was revised by Nancy Lea Eik-Nes.
Cite this paper
Khan, N.H., Tegnander, E., Dreier, J.M., Eik-Nes, S., Torp, H. and Kiss, G. (2017) Automatic Detection and Measurement of Fetal Biparietal Diameter and Femur Length―Feasibility on a Portable Ultrasound De- vice. Open Journal of Obstetrics and Gynecology, 7, 334-350. https://doi.org/10.4236/ojog.2017.73035
References
- 1. Eik-Nes, S.H. (1993) The Fetal Examination. Ultrasound in Obstetrics & Gynecology, 3, 83-85.
https://doi.org/10.1046/j.1469-0705.1993.03020083.x - 2. Salomon, L., Alfirevic, Z., Bilardo, C., Chalouhi, G., Ghi, T., Kagan, K., Lau, T., Papageorghiou, A., Raine-Fenning, N., Stirnemann, J., et al. (2013) ISUOG Practice Guidelines: Performance of First-Trimester Fetal Ultrasound Scan. Ultrasound in Obstetrics & Gynecology, 41, 102-113.
https://doi.org/10.1002/uog.12342 - 3. Khan, N.H., Tegnander, E., Dreier, J.M., Eik-Nes, S., Torp, H. and Kiss, G. (2014) Automatic Measurement of Biparietal Diameter with a Portable Ultrasound Device, in: Ultrasonics Symposium (IUS), 2014 IEEE International. IEEE, 459-462.
- 4. Khan, N.H., Tegnander, E., Dreier, J.M., Eik-Nes, S., Torp, H. and Kiss, G. (2015) Automatic Detection and Measurement of Fetal Femur Length Using a Portable Ultrasound Device, in: Ultrasonics Symposium (IUS), 2015 IEEE International. IEEE, 1-4.
https://doi.org/10.1109/ultsym.2015.0486 - 5. Okland, I., Gjessing, H., Grottum, P., Eggebo, T. and Eik-Nes, S. (2011) A New Population Based Term Prediction Model vs. Two Traditional Sample-Based Models: Validation on 9046 Ultrasound Examinations. Ultrasound in Obstetrics & Gynecology, 37, 207-213.
https://doi.org/10.1002/uog.7728 - 6. Campbell, S. and Thoms, A. (1977) Ultrasound Measurement of the Fetal Head to Abdomen Circumference Ratio in the Assessment of Growth Retardation. BJOG, 84, 165-174.
https://doi.org/10.1111/j.1471-0528.1977.tb12550.x - 7. Gjessing, H., Grottum, P. and Eik-Nes, S. (2007) A Direct Method for Ultrasound Prediction of Day of Delivery: A New, Population-Based Approach. Ultrasound in Obstetrics & Gynecology, 30, 19-27.
https://doi.org/10.1002/uog.4053 - 8. Queenan, J., O’brien, G. and Campbell, S. (1980) Ultrasound Measurement of Fetal Limb Bones. American Journal of Obstetrics & Gynecology, 138, 297-302.
https://doi.org/10.1016/0002-9378(80)90252-5 - 9. Perni, S., Chervenak, F., Kalish, R., Magherini-Rothe, S., Predanic, M., Streltzoff, J. and Skupski, D. (2004) Intraobserver and Interobserver Reproducibility of Fetal Biometry. Ultrasound in Obstetrics & Gynecology, 24, 654-658.
https://doi.org/10.1002/uog.1717 - 10. Carneiro, G., Georgescu, B., Good, S. and Comaniciu, D. (2008) Detection and Measurement of Fetal Anatomies from Ultrasound Images Using a Constrained Probabilistic Boosting Tree. Transactions on Medical Imaging, 27, 1342-1355.
https://doi.org/10.1109/TMI.2008.928917 - 11. Hanna, C.W. and Youssef, A. (1997) Automated Measurements in Obstetric Ultrasound Images. Processing of the International Conference on Image, 3, 504-507.
https://doi.org/10.1109/icip.1997.632168 - 12. Lu, W., Tan, J. and Floyd, R. (2005) Automated Fetal Head Detection and Measurement in Ultrasound Images by Iterative Randomized Hough Transform. Ultrasound in Medicine and Biology, 31, 929-936.
https://doi.org/10.1016/j.ultrasmedbio.2005.04.002 - 13. Mukherjee, P., Swamy, G., Gupta, M., Patil, U. and Krishnan, K.B. (2010) Automatic Detection and Measurement of Femur Length from Fetal Ultrasonography. Proceedings of SPIE 7629, Medical Imaging 2010: Ultrasonic Imaging, Tomography, and Therapy, 762909.
https://doi.org/10.1117/12.844340 - 14. Pathak, S.D., Chalana, V. and Kim, Y. (1997) Interactive Automatic Fetal Head Measurements from Ultrasound Images Using Multimedia Computer Technology. Ultrasound in Medicine and Biology, 23, 665-673.
https://doi.org/10.1016/S0301-5629(97)00009-4 - 15. Thomas, J.G., Peters, R.A. and Jeanty, P. (1991) Automatic Segmentation of Ultrasound Images Using Morphological Operators. IEEE Transactions on Medical Imaging, 10, 180-186.
- 16. Wang, C.-W. (2014) Automatic Entropy-Based Femur Segmentation and Fast Length Measurement for Fetal Ultrasound Images. 2014 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Taipei, 6-8 June 2014, 1-5.
- 17. Altman, D. and Chitty, L. (1997) New Charts for Ultrasound Dating of Pregnancy. Ultrasound in Obstetrics & Gynecology, 10, 174-191.
https://doi.org/10.1046/j.1469-0705.1997.10030174.x - 18. Orderud, F. (2010) Real-Time Segmentation of 3D Echocardiograms Using a State Estimation Approach with Deformable Models. PhD Thesis, NTNU, Norway.
- 19. Canny, J. (1986) A Computational Approach to Edge Detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-8, 679-698.
- 20. Sobel, I. and Feldman, G. (1968) A 3 × 3 Isotropic Gradient Operator for Image Processing. The Stanford Artificial Intelligence Project, 271-272.
- 21. Kimme, C., Ballard, D. and Sklansky, J. (1975) Finding Circles by an Array of Accumulators. Communications of the ACM, 18, 120-122.
https://doi.org/10.1145/360666.360677 - 22. Bradski, G. and Kaehler, A., (2008) Learning OpenCV: Computer Vision with the OpenCV Library. “O’Reilly Media, Inc.”, California.
- 23. Kiryati, N., Eldar, Y. and Bruckstein, A.M. (1991) A Probabilistic Hough Transform. Pattern Recognition, 24, 303-316.
- 24. Matas, J., Galambos, C. and Kittler, J. (2000) Robust Detection of Lines Using the Progressive Probabilistic Hough Transform. Computer Vision and Image Understanding, 78, 119-137.
- 25. Okland, I., Gjessing, H., Grottum, P. and Eik-Nes, S. (2010) Biases of Traditional Term Prediction Models: Results from Different Sample-Based Models Evaluated on 41343 Ultrasound Examinations. Ultrasound in Obstetrics & Gynecology, 36, 728-734.
https://doi.org/10.1002/uog.7707 - 26. Okland, I., Nakling, J., Gjessing, H.K., Grottum, P. and Eik-Nes, S.H. (2012) Advantages of the Population-Based Approach to Pregnancy Dating: Results from 23020 Ultrasound Examinations. Ultrasound in Obstetrics & Gynecology, 39, 563-568.
https://doi.org/10.1002/uog.10081 - 27. Hadlock, F., Harrist, R., Carpenter, R., Deter, R. and Park, S. (1984) Sonographic Estimation of Fetal Weight. The Value of Femur Length in Addition to Head and Abdomen Measurements. Radiology, 150, 535-540.
https://doi.org/10.1148/radiology.150.2.6691115 - 28. Shepard, M., Richards, V., Berkowitz, R., Warsof, S. and Hobbins, J. (1982) An Evaluation of Two Equations for Predicting Fetal Weight by Ultrasound. American Journal of Obstetrics & Gynecology, 142, 47-54.
https://doi.org/10.1016/S0002-9378(16)32283-9 - 29. Gjessing, H.K., Grttum, P., Okland, I. and Eik-Nes, S.H. (2016) Fetal Weight Monitoring and Birth Weight Prediction: A New Population-Based Approach. Ultrasound in Obstetrics & Gynecology.










