Open Journal of Ecology
Vol.3 No.2(2013), Article ID:31242,12 pages DOI:10.4236/oje.2013.32016
What elk, wolves and caterpillars have in common—The perfect forager theorem
![]()
1Parks Division, Alberta Tourism, Parks and Recreation, Edmonton, Canada; *Corresponding Author: pweclaw@ecoremus.com
2Renewable Resources, Faculty of Agricultural, Life and Environmental Sciences, University of Alberta, Edmonton, Canada
Copyright © 2013 Piotr Weclaw, Robert J. Hudson. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 9 January 2013; revised 15 February 2013; accepted 15 March 2013
Keywords: Resource Optimization; Optimal Use of Resources; Optimal Foraging; Perfect Forager Theorem; Functional Response Curve; Ecological Modeling; Marginal Value Theorem; Foraging Behaviour; Computer Model; SeekSMART
ABSTRACT
It is widely accepted that the Marginal Value Theorem (MVT) describes optimal foraging strategies of animals and the mechanism proposed by the MVT has been supported by a number of field observations. However, findings of many researchers indicate that in natural conditions foragers do not always behave according to the MVT. To address this inconsistency, in a series of computer simulation experiments, we examined the behaviour of four types of foragers having specific foraging efficiencies and using the MVT strategies in 15 different landscapes in an ideal environment (no intra-and inter-specific interactions). We used data on elk (Cervus elaphus) to construct our virtual forager. Contrary to the widely accepted understanding of the MVT (residence time in a patch should be longer in environments where travel time between patches is longer) we found that in environments with the same average patch quality and varying average travel times between patches, patch residence times of some foragers are not affected by travel times. Based on our analysis we propose a mechanism responsible for this observation and formulate the perfect forager theorem (PFT). We also introduce the concepts of a foraging coefficient (F) and foragers’ hub (α), and propose a model to describe the relationship between the perfect forager and all other forager types.
1. INTRODUCTION
Nutritional status and energy budgets are key determinants of survival and reproductive success of animals. A variety of parameters affect the availability and accessibility of food for wildlife and, to utilize forage resources, each individual needs to respond to these environmental factors. Individual animals have specific abilities to exploit available resources and may use different foraging strategies to satisfy their food requirements. It is widely accepted that the Marginal Value Theorem (MVT) [1] explains the foraging behavior and describes the optimal foraging strategy. Therefore, the MVT forms the foundation of the classical foraging theory that is fundamental to behavioral ecology. The MVT, derived from observations of foraging behavior of Great Tits (Parus major), received support from several field studies [2-7]. Some authors [8-11], however, argued that foraging strategies other than the MVT could be used by foragers.
The deviations from the MVT were believed to result from the imperfect knowledge that animals have about their environment and interand intra-species interactions [12]. It was argued [10] that the reason for refuting the MVT by several studies [9,13-17] is that MVT lacks biological realism.
If these predictions [10,11,17] were true, then a healthy animal secure from predation and not exposed to competition for forage resources, or other intra and inter-species interactions, occurring outside the breeding season, should always follow the MVT while foraging. The vast research that contradicts the MVT (including simulation studies [9]), suggests that the lack of biological realism of the MVT may be an insufficient explanation for animals not following the MVT model and may not account for all factors responsible for the observed deviations from the MVT. It is logical to assume that the intrinsic ability of foragers to utilize forage resources could have consequences for the foraging strategies that animals employ. However, many papers (e.g. [5,10,11]) that assess foraging strategies in the context of the MVT do not consider the forager’s functional response and its consequences for an animal’s foraging strategy.
The first goal of this research was to examine the behavior of different foragers (having specific foraging efficiency defined by the slope of the functional response curve) using MVT strategies under ideal conditions (i.e., no interor intra-species interactions), with perfect knowledge of the landscape, and across a spectrum of habitats with varying average patch quality and average travel time. We expected that each forager, as predicted by the MVT, depending on the shape of its functional response curve, should behave differently when using the MVT as its foraging strategy. Therefore, there should be behavioral differences among foragers associated with their specific foraging efficiencies if they are using the MVT. Our second and main goal was to describe, in a form of a mathematical model, the potential relationships between the observed behaviors (patch residence times, Tr) of foragers with different foraging efficiencies feeding in different landscapes.
Based on a series of simulation experiments, we propose a mathematical model that describes the behavior of different foragers in response to specific landscape characteristics when maximizing their forage consumption even if environmental noise is not present. By doing this, we formulate the perfect forager theorem that defines a forager not affected by the distribution of patches across the landscape and propose a relationship that exists between the perfect forager and all other forager types. To describe the perfect forager we introduce the concepts of a foraging coefficient F and foragers’ hub α.
2. METHODS
To set the discussion in a specific context we chose elk (Cervus elaphus) as an experimental subject. The ecology and foraging behavior of elk are very well documented. This availability of data and the ecological plasticity of elk make this species an ideal subject for a simulation modeling study and allow for parameterization of all components of a simulation model with real field data.
To address our research questions, using STELLA Research [18] modeling software, we built and employed a computer simulation model called SeekSMART. A detailed discussion of the structure of this comprehensive simulation model is provided elsewhere [19]. In this paper we provide a short overview of the main characteristics of the model necessary for understanding the simulations and their outputs.
SeekSMART is a mechanistic and deterministic model that describes foraging by a virtual animal in a simulated landscape. It assumes that at the start of a simulation run the animal is located at a specific point in a predefined landscape consisting of patches of arbitrarily assigned biomasses of forage and distributed according to the assigned travel times among the patches. From the starting point, the animal has to travel to patch N for a userspecified units of time. Upon entering patch N, the forager has to decide whether to stay within this patch and start foraging, or whether to skip the patch and start traveling to patch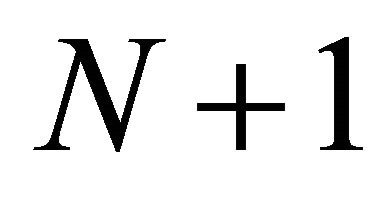 . This decision, as well as the forager’s next decision on how long to feed in a patch, are made by the animal based on the foraging strategy that it uses according to the parameters specified in the model. The following 4 rules defining the patch leaving decisions can be examined in SeekSMART:
. This decision, as well as the forager’s next decision on how long to feed in a patch, are made by the animal based on the foraging strategy that it uses according to the parameters specified in the model. The following 4 rules defining the patch leaving decisions can be examined in SeekSMART:
1) The forager leaves the current patch when the density of forage available in the current patch drops to an arbitrary assigned value (the forager may or may not know the landscape);
2) The forager leaves the current patch when the density of forage available in the current patch drops to the average of forage density in all patches (assumes that the forager knows the landscape);
3) The forager follows the Marginal Value Theorem (MVT). In this case, the average travel time between patches and the forager’s gain curve from the average patch determine when the forager leaves the current patch ![]() and moves to the next patch
and moves to the next patch 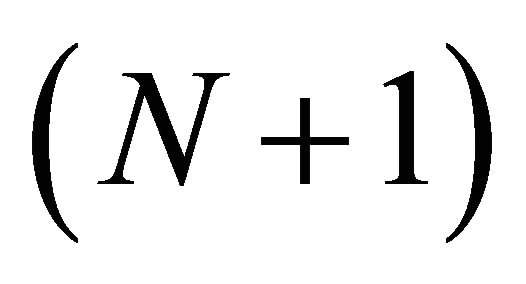 (assumes the forager knows the landscape);
(assumes the forager knows the landscape);
4) The forager feeds in a patch for an arbitrary assigned patch residence time 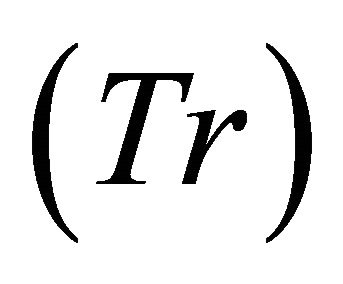 (the forager may or may not know the landscape).
(the forager may or may not know the landscape).
While feeding within a patch, the forager’s consumption rate is driven by the functional response curve [20] described by the following equation that is generally accepted as a formula explaining type II functional response curve (FRC) for foraging ungulates [21-23]:
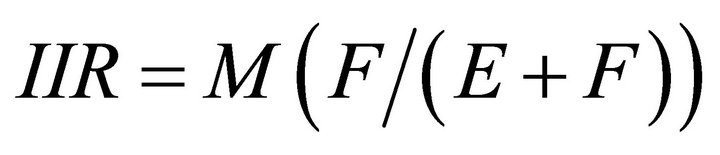 (1)
(1)
where:
IIR—instantaneous intake rate (g/hr);
M—asymptotic (or maximum) intake (g/hr);
F—density of available forage biomass (kg/ha);
E—efficiency of the forager: the forage biomass density (kg/ha) at which the instantaneous intake rate equals half of the maximum intake rate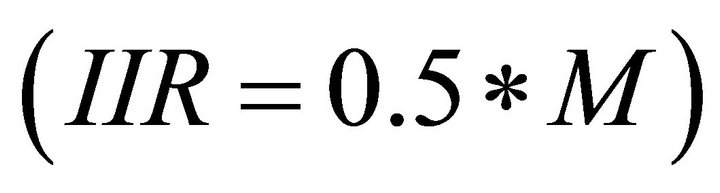 .
.
Therefore, the instantaneous intake rate (IIR) is determined by two parameters specific to the forager: the maximum intake (M) and efficiency (E). By adjusting the maximum intake rate (M) and the efficiency (E) of the forager, any shape of type II functional response curve can be assigned to the forager. This allows for examination of different foragers of any foraging efficiency.
The forager continues to feed within the patch until either its gut is full or if the time to leave the patch, based on the forager’s strategy has elapsed. After leaving patch N the forager travels to patch 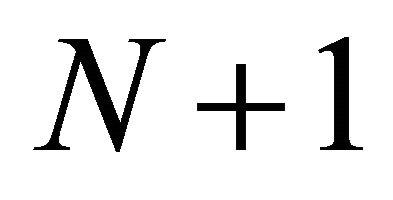 and the process described above starts again. A forager may use the same foraging strategy defined at the onset of the simulation run for the entire total time of the run, or its foraging strategy can be changed at any given time by adjusting the parameters that define the forager and the landscape.
and the process described above starts again. A forager may use the same foraging strategy defined at the onset of the simulation run for the entire total time of the run, or its foraging strategy can be changed at any given time by adjusting the parameters that define the forager and the landscape.
SeekSMART allows for defining the following landscape characteristics by adjusting the main attributes of the patches:
1) Initial patch biomass density (kg/ha)-IPBD;
2) Patch size (m2)-PS;
3) Initial patch biomass (g)-IPB. This value is calculated by the model based on the values provided for PS and IPBD;
4) Distances between patches expressed as travel time (h)-Tt.
Additionally, the following settings of the landscape can be specified in the model allowing examination of the effects of distribution of patches, their initial biomass densities, and overall landscape productivity:
1) All forage patches are equal (they have the same initial forage biomass density);
2) Patches are different, i.e., every patch has a unique initial forage biomass density;
3) Travel time between patches is the same and can have any value including zero;
4) Travel time between patches is not equal. Travel time between any consecutive patches can be arbitrary assigned and can have any value including zero.
2.1. Scenarios
Based on the reported values of available forage biomass in elk habitat [22,23], we created three main types of landscape depending on the average patch biomass. Landscapes of type A were poor landscapes with low resources. The range of the initial patch biomass densities (IPBD) across all patches was 1000 kg/ha ± 30% (850 - 1150 kg/ha). Landscapes of type B were of medium productivity with the IPBD within the range of 2000 kg/ha ± 30% (1700 - 2300 kg/ha). Landscapes of type C were the most productive habitats and the IPBD was within the range of 3000 kg/ha ± 30% (2550 - 3450). To avoid bias, instead of arbitrarily assigning IPBD for each individual patch, we used STELLA Research [18] to randomly generate these values within each of the three landscape types. Landscapes of type A had a mean IPBD of 1008.8 kg/ha (range: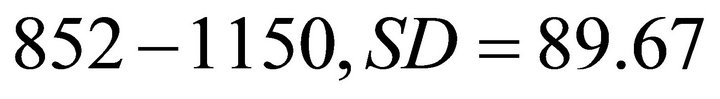 ), IPBD was 2035 (range:
), IPBD was 2035 (range: ) and 3011.3 kg/ha (range
) and 3011.3 kg/ha (range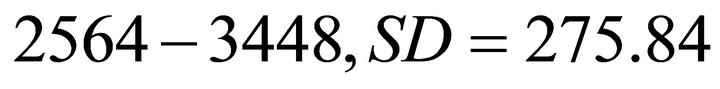 ) for Landscapes of type B and C respectively. Because patch biomass assigned to Landscapes type C seemed most realistic, we started with Landscapes C and used five average travel times (Tt): 0.1 h, 0.5 h, 1.0 h, 2 h and 4.0 h. These values were assigned arbitrarily with a range of ±0.1 h. STELLA Research’s random number generator was used to assign a specific Tt for each patch within the above ranges. This resulted in five landscapes of type C: CT1, CT2, CT3, CT4 and CT5. Although the patches (and the average IPBD) were the same for all these five landscapes, landscape CT1 was most productive (the average Tt was 0.1 h) and the overall productivity of the landscape was lower for the consecutive landscapes and lowest for landscape CT5 where the average Tt was 4 h. We used the same approach for landscapes of type B and A (created landscapes: AT1, AT2, AT3, AT4, AT5, and BT1, BT2, BT3, BT4, BT5) to vary their forage productivity while keeping the same average IPBDs specific for all five landscape sub-types. This resulted in 60 scenarios (four foragers feeding in 15 landscapes) (Figure 1).
) for Landscapes of type B and C respectively. Because patch biomass assigned to Landscapes type C seemed most realistic, we started with Landscapes C and used five average travel times (Tt): 0.1 h, 0.5 h, 1.0 h, 2 h and 4.0 h. These values were assigned arbitrarily with a range of ±0.1 h. STELLA Research’s random number generator was used to assign a specific Tt for each patch within the above ranges. This resulted in five landscapes of type C: CT1, CT2, CT3, CT4 and CT5. Although the patches (and the average IPBD) were the same for all these five landscapes, landscape CT1 was most productive (the average Tt was 0.1 h) and the overall productivity of the landscape was lower for the consecutive landscapes and lowest for landscape CT5 where the average Tt was 4 h. We used the same approach for landscapes of type B and A (created landscapes: AT1, AT2, AT3, AT4, AT5, and BT1, BT2, BT3, BT4, BT5) to vary their forage productivity while keeping the same average IPBDs specific for all five landscape sub-types. This resulted in 60 scenarios (four foragers feeding in 15 landscapes) (Figure 1).
To assess the consequences of foraging by different foragers in landscapes of different productivity at a small scale, we examined four types of foragers by assigning four different values of parameter E (efficiency) and maintaining all other parameters that define the virtual forager unchanged. This resulted in the following four types of foragers: extremely efficient forager (EE forager), efficient forager (E forager), medium efficiency forager (ME forager), and low efficiency forager (LE forager) (Figure 2).
For ME Forager, we used the default value of 486.61 kg/ha for parameter E [22,23]. To test a wide spectrum of foragers we next increased the value of E by 80% to 875.88 kg/ha and decreased it by 80% to 97.32 kg/ha to simulate LE and E forgers respectively. To examine very

Figure 1. The three different types of landscapes defined by patch quality and divided into specific 15 landscapes depending on the average travel time (Tt) between patches.
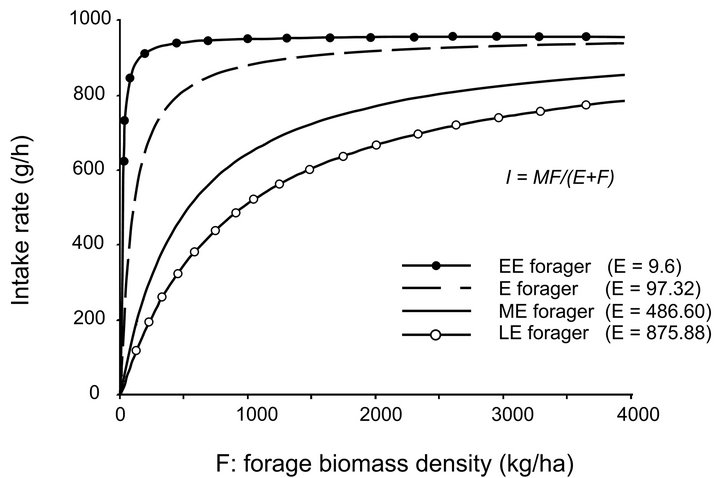
Figure 2. Functional response curves of the four forager types (EE: E = 9.60, E: E = 97.32, ME: E = 486.60, LE: E = 875.88) tested in the model. If the value of the maximum intake rate (M) is constant, then the forager’s efficiency (E) defines the slope of its functional response curve.
efficient foragers reported in literature [24] and a potential relationship between the maximum intake rate (M) and efficiency (E), we also tested EE forager ( kg/ha).
kg/ha).
To obtain gain functions (forage consumed from a patch as a function of time) that could be next used in calculating the residence times (Tr) for the foragers using the MVT strategies, we performed initial runs with foragers feeding in the average patches (IPBD, Tt, and PS) in each landscape until forage biomass in the patch was completely depleted (dropped to 0 g). These initial runs generated curves that described gains from average patches and allowed for assessing the residence times (Tr) of animals following the MVT. These were next used for further analysis and model validation.
2.2. Model Validation
To validate the model and test the daily (24 h) behavior of the virtual elk in SeekSMART, we used values, provided by several studies [4,22,23,25,26] which were the default values for the parameters in the model. A random number generator was used to assign individual characteristics of each patch for the first 20 patches in the feeding sequence (according to [4,27] an elk should forage in about 9 patches during the 24 h period) (Table 1). This resulted in unequal patches (each patch had a unique IPBD) and unique travel time for each patch with an average of 0.1 h (6 minutes). In other words, the virtual elk in the validation run was a ME forager that foraged in landscape CT1. When foraging, the virtual elk applied the MVT [4], which means that the animal stayed and fed in the patch until the forage density in the patch was equal to the giving-up-density (GUD) obtained at the end of the residence time (Tr) in the initial runs that were used for examining foraging within the average patch and obtaining gain functions in landscape CT1.
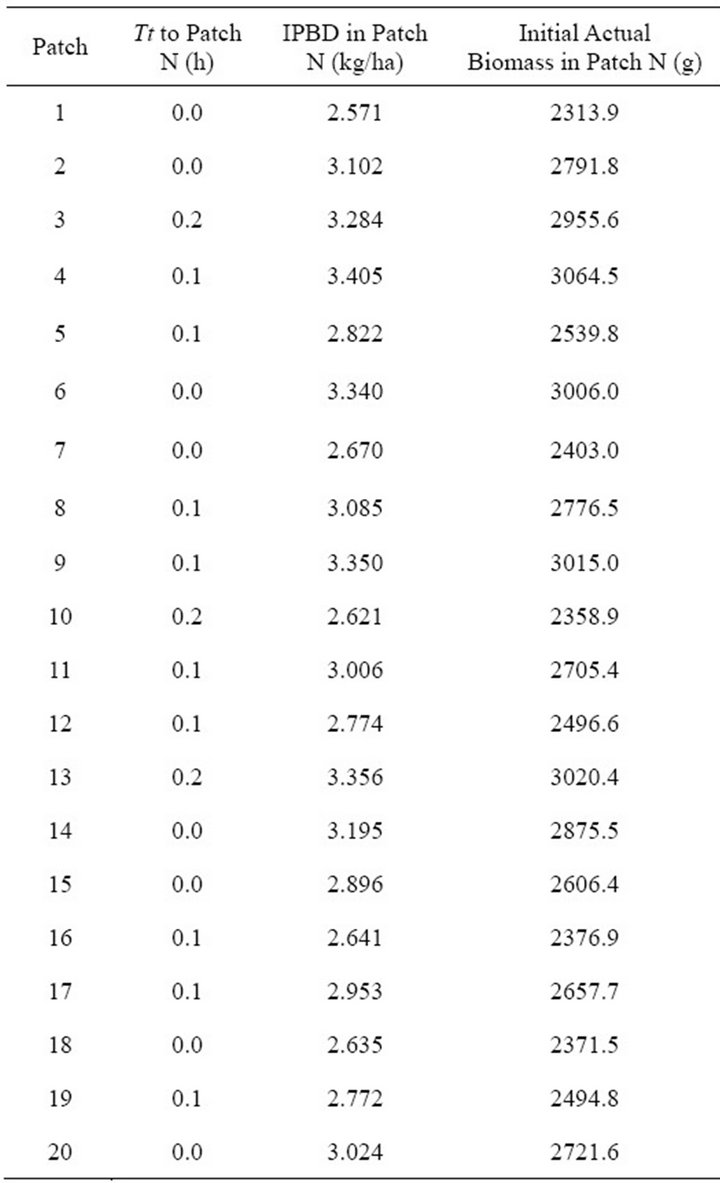
Table 1. Characteristics of the first 20 individual patches of forage in Landscape CT1 in the model validation run.
3. RESULTS
3.1. Scenarios
As predicted by the MVT, travel time (Tt) and patch biomass (IPBD) affected patch residence time (Tr) of some foragers. However, contrary to MVT predictions, Tt did not affect Tr of all foragers (Tables 2-4).
In landscapes of type C, the longest Tr was 4.2 h resulting from a combination of long average travel time (4 h), high average patch biomass (initial average patch biomass = 2710 g) and low efficiency of the forager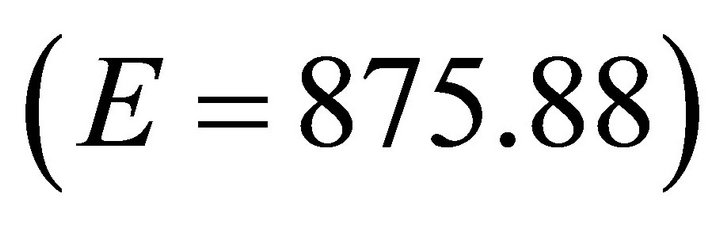 . The shortest Tr for Landscapes of type C was 1.3 h and was associated with the low efficiency of the forager
. The shortest Tr for Landscapes of type C was 1.3 h and was associated with the low efficiency of the forager 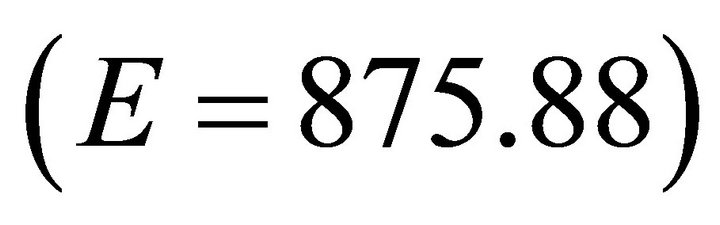 feeding in a landscape with shortest travel times (average
feeding in a landscape with shortest travel times (average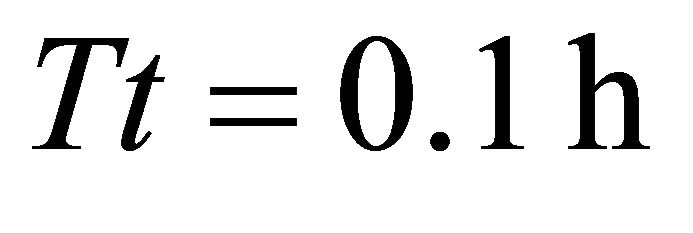 ). Forage consumed from the average patch in landscapes of type C varied from 992 to 2710 g. The extremely efficient (EE) forager
). Forage consumed from the average patch in landscapes of type C varied from 992 to 2710 g. The extremely efficient (EE) forager 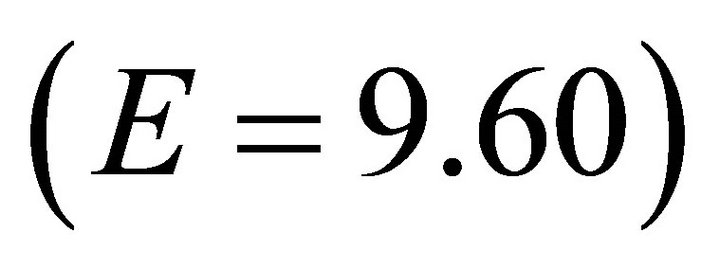 was able to achieve the highest consumption from the average patch in four scenarios within the following four landscapes: CT2, CT3, CT4
was able to achieve the highest consumption from the average patch in four scenarios within the following four landscapes: CT2, CT3, CT4
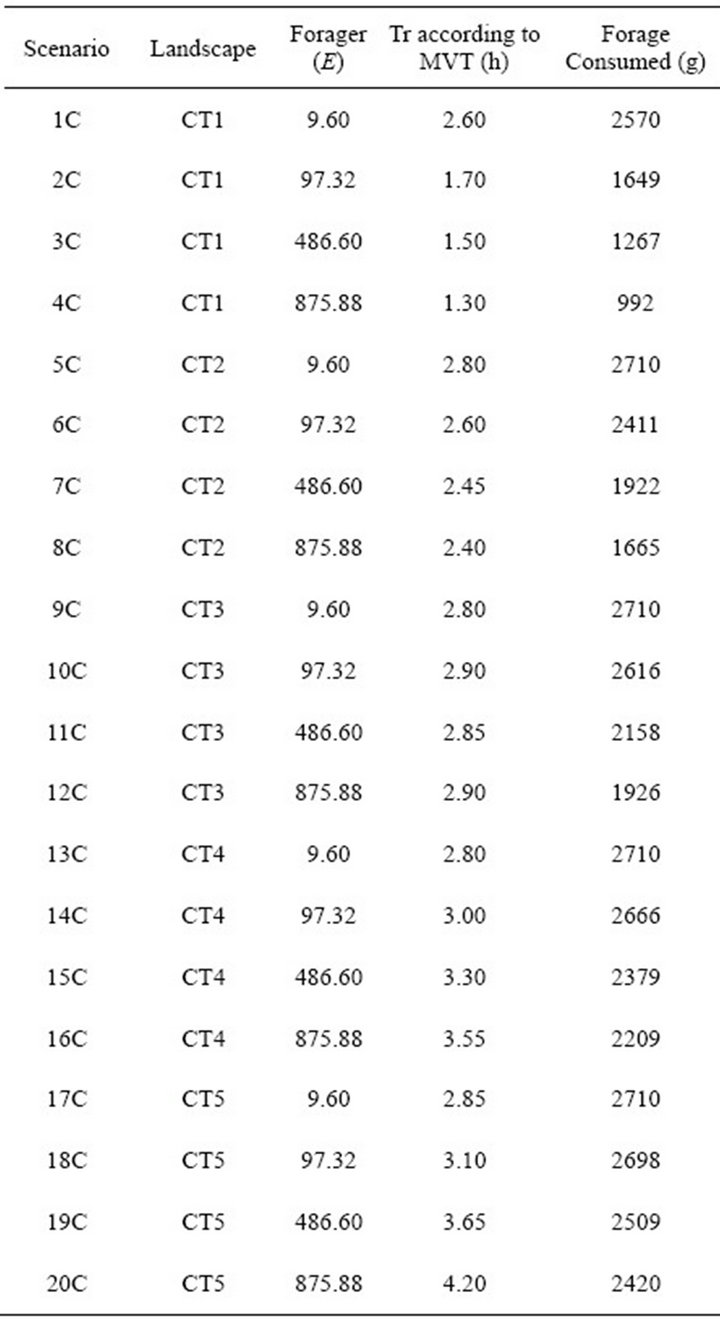
Table 2. Patch residence times (Tr) and associated forage consumed obtained by applying the MVT to five types of foragers in landscapes of Type C.
and CT5. In these landscapes, the maximum amount of forage consumed by the EE forager was the same as the initial amount of forage in the patch (2710 g) indicating that the animal was able to deplete the patch completely. The EE forager was not able to deplete the average patch only in one scenario with the shortest average travel time (average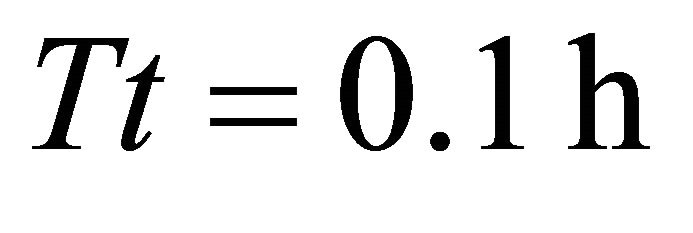 , landscape CT1) when its total consumption at the end of the residence time
, landscape CT1) when its total consumption at the end of the residence time 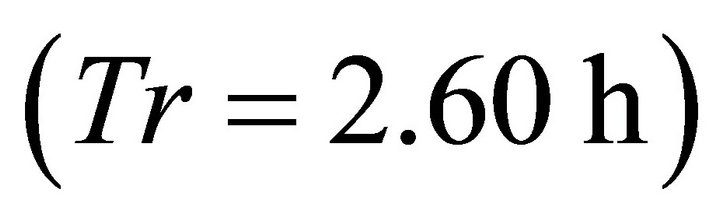 was 2570 g leaving 140 g of forage in the patch. In the same landscape, with the same shortest travel time (0.1 h), the LE forager left the patch at
was 2570 g leaving 140 g of forage in the patch. In the same landscape, with the same shortest travel time (0.1 h), the LE forager left the patch at 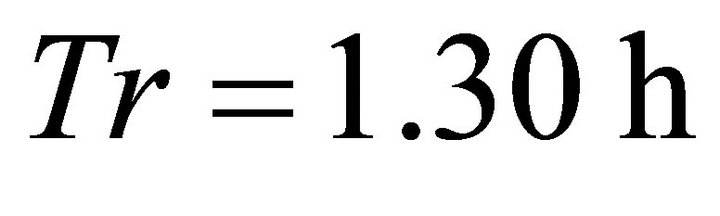 (note a 50% shorter Tr than the Tr of the EE forager) consuming only 992 g (the lowest consumption in all types of Landscape C for all foragers). An interesting trend can be noted in the outputs (Tables 2-4). The EE forager had the
(note a 50% shorter Tr than the Tr of the EE forager) consuming only 992 g (the lowest consumption in all types of Landscape C for all foragers). An interesting trend can be noted in the outputs (Tables 2-4). The EE forager had the

Table 3. Patch residence times (Tr) and associated forage consumed obtained by applying the MVT to five types of foragers in landscapes of Type B.
longest residence time of all foragers feeding in a landscape with the shortest average travel time (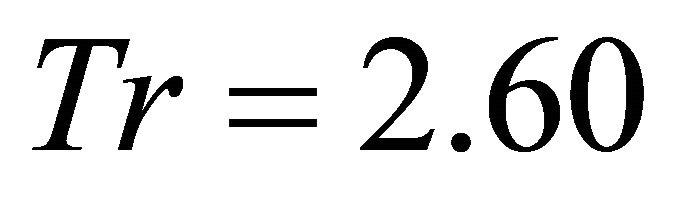 , average
, average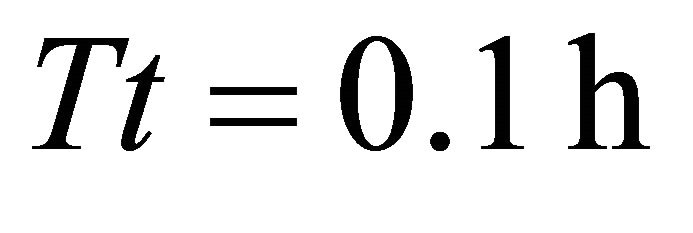 ). However, in the landscape with the longest average travel time (average
). However, in the landscape with the longest average travel time (average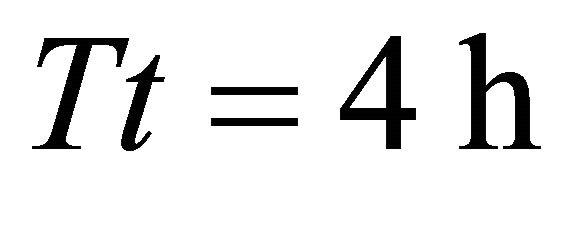 ) the EE forager had the shortest residence time
) the EE forager had the shortest residence time  of all foragers. Increasing the average travel time by 4000% (from 0.1 to 4.0 h) resulted in an increase of the Tr of the EE forager by 9.62% and by 323.08% for the LE forager.
of all foragers. Increasing the average travel time by 4000% (from 0.1 to 4.0 h) resulted in an increase of the Tr of the EE forager by 9.62% and by 323.08% for the LE forager.
Foraging in Landscapes of type B by all four foragers resulted in shorter Tr (range of 0.8 to 3.2 h) which was the outcome of a lower quality of patches (lower average IPBD) as compared to landscapes C and was consistent with the common understanding of the MVT. It is interesting to note that, similarly to Landscapes C, both the longest and the shortest Tr were associated with the LE

Table 4. Patch residence times (Tr) and associated forage consumed obtained by applying the MVT to five types of foragers in landscapes of type A.
forger. The shortest residence time (0.8 h) that resulted from the LE forager feeding in landscape BT1 (average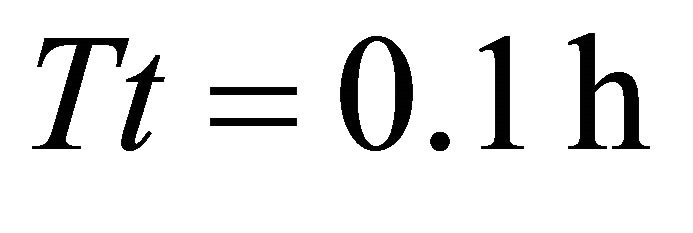 ) allowed the animal to consume 574 g from the average patch. The same (LE) forager attained consumption of 1598 g from the average patch when feeding in landscape BT5 (average
) allowed the animal to consume 574 g from the average patch. The same (LE) forager attained consumption of 1598 g from the average patch when feeding in landscape BT5 (average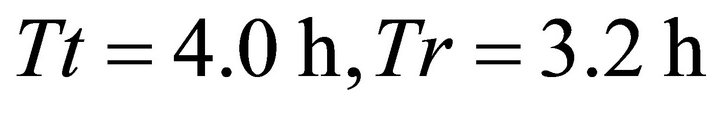 ). The highest consumption was achieved by the EE forager that consumed 1832 g by staying for 1.9 h in the average patch of landscapes BT2 (average
). The highest consumption was achieved by the EE forager that consumed 1832 g by staying for 1.9 h in the average patch of landscapes BT2 (average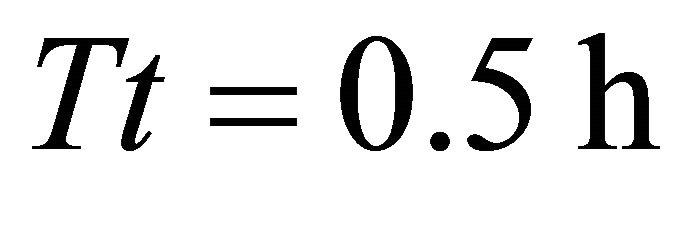 ) and BT5 (average
) and BT5 (average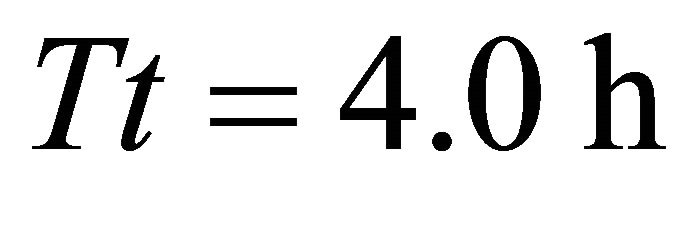 ). In both these scenarios the EE forager was able to completely deplete the average patches (average initial patch biomass for all scenarios in Landscapes B was 1832 g). The EE forager had similar gains in Landscapes BT3 and BT4 (1815 g) and only in Landscape BT1 its forage consumption was considerably lower (1662 g after leaving the patch at
). In both these scenarios the EE forager was able to completely deplete the average patches (average initial patch biomass for all scenarios in Landscapes B was 1832 g). The EE forager had similar gains in Landscapes BT3 and BT4 (1815 g) and only in Landscape BT1 its forage consumption was considerably lower (1662 g after leaving the patch at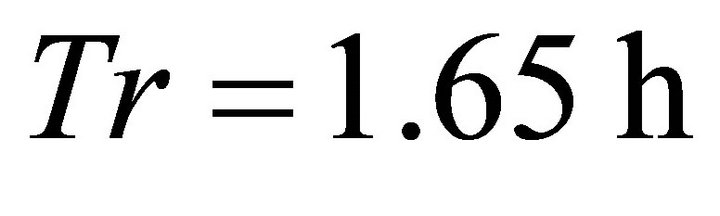 ). It is interesting to note in Landscape B the same trend that was observed in Landscape C: the EE forager had the longest Tr (1.65 h) of all foragers in a landscape with the shortest travel times (BT1, average
). It is interesting to note in Landscape B the same trend that was observed in Landscape C: the EE forager had the longest Tr (1.65 h) of all foragers in a landscape with the shortest travel times (BT1, average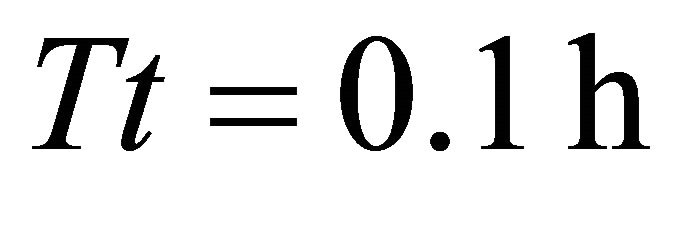 ) and the same (EE) forager had the shortest Tr (1.9 h) in the landscape with the longest travel times (average
) and the same (EE) forager had the shortest Tr (1.9 h) in the landscape with the longest travel times (average 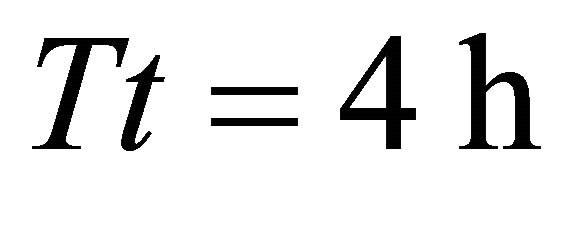 at BT5). Increasing the average travel time among patches by 4000% resulted in an increase of the residence time of the EE forager by 15.15% and by 400% for the LE forager.
at BT5). Increasing the average travel time among patches by 4000% resulted in an increase of the residence time of the EE forager by 15.15% and by 400% for the LE forager.
As expected, residence times in Landscapes of type A were shortest and had smaller range than in more productive landscapes. The shortest Tr was 0.55 h and was associated with the ME forager feeding in a landscape with shortest travel times (average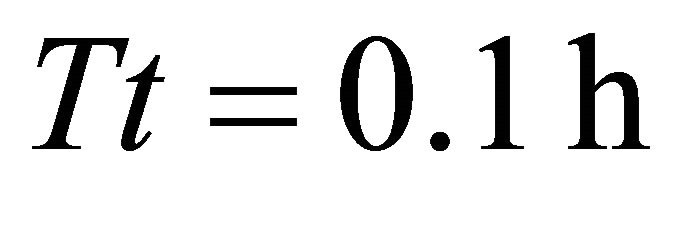 ). The LE forager had very similar Tr (0.6 h) in the same landscape (AT1). In landscape AT1 the ME forager and the LE forager consumed 389 and 329 g respectively from the average patch. Similarly to Landscapes of type C and B, the longest residence time
). The LE forager had very similar Tr (0.6 h) in the same landscape (AT1). In landscape AT1 the ME forager and the LE forager consumed 389 and 329 g respectively from the average patch. Similarly to Landscapes of type C and B, the longest residence time 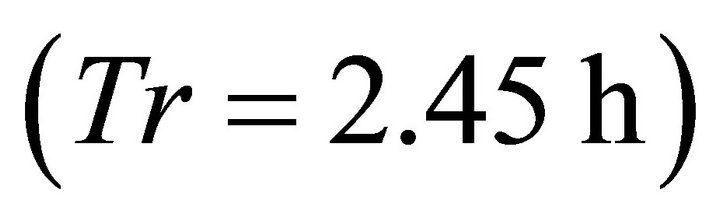 was associated with the LE forager feeding in the landscape with longest travel times (AT5, average
was associated with the LE forager feeding in the landscape with longest travel times (AT5, average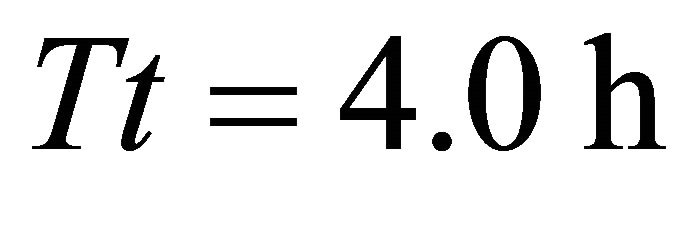 ). In landscapes of type A, the highest consumption (908 g) was again achieved by the EE forager feeding in three landscapes: AT3 (average
). In landscapes of type A, the highest consumption (908 g) was again achieved by the EE forager feeding in three landscapes: AT3 (average ), AT4 (average
), AT4 (average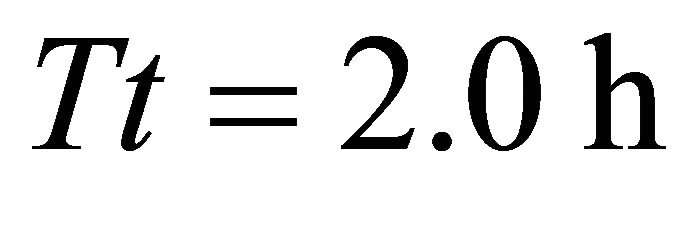 ), AT5 (average
), AT5 (average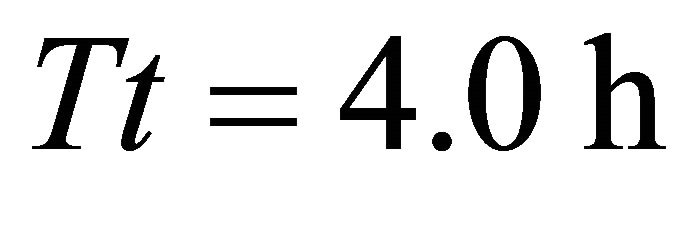 ) for a residence time (Tr) of 0.95 (AT3) and 1.00 h (landscapes AT4 and AT5). This highest consumption was equal to the initial biomass of forage in the average patch. Because the smallest time unit in SeekSMART was 0.1 h, the patch residence time (0.95) for the EE forager in landscape AT3 should be rounded to 1:00 h. It can be then calculated that the EE forager required 1:00 h to completely deplete the patch in 3 scenarios with the longest, second longest the third longest average travel times (initial average patch biomass was 908 g in all scenarios in landscapes of type A). It was the LE forager that had the lowest consumption from the average patch at 329 g when feeding for 0.6 h in the average patch of landscape AT1 (average
) for a residence time (Tr) of 0.95 (AT3) and 1.00 h (landscapes AT4 and AT5). This highest consumption was equal to the initial biomass of forage in the average patch. Because the smallest time unit in SeekSMART was 0.1 h, the patch residence time (0.95) for the EE forager in landscape AT3 should be rounded to 1:00 h. It can be then calculated that the EE forager required 1:00 h to completely deplete the patch in 3 scenarios with the longest, second longest the third longest average travel times (initial average patch biomass was 908 g in all scenarios in landscapes of type A). It was the LE forager that had the lowest consumption from the average patch at 329 g when feeding for 0.6 h in the average patch of landscape AT1 (average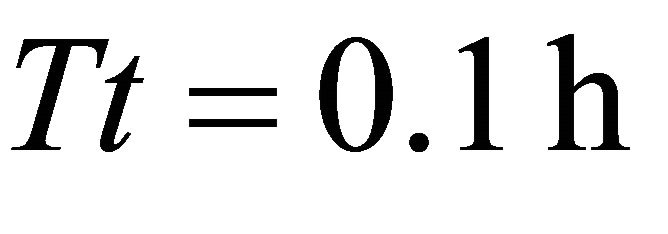 ).
).
In Landscapes of type A, we observed the same trend that was prevalent in Landscapes of types C and B: the EE forager had the longest Tr of all four types of foragers in a landscape with the shortest average travel time (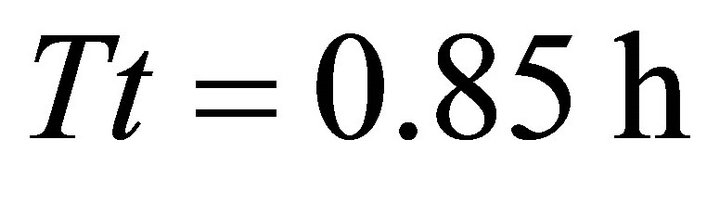 in AT1 with average
in AT1 with average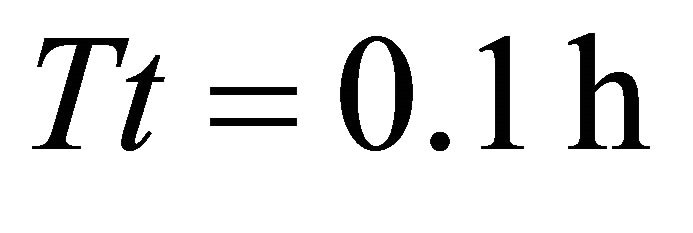 ). It also had the shortest
). It also had the shortest 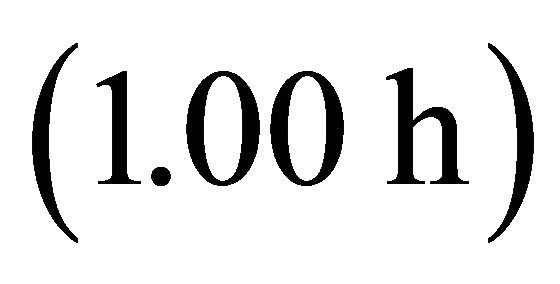 Tr of all four foragers in a landscape with the longest average travel time (AT5, average
Tr of all four foragers in a landscape with the longest average travel time (AT5, average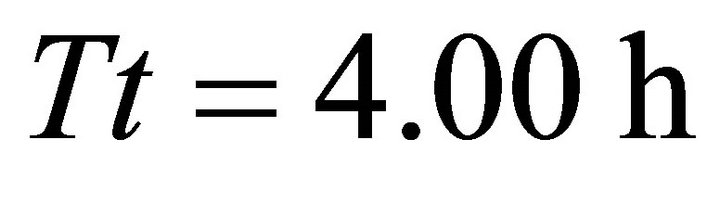 ). Increasing the average travel time by 4000% resulted in an increase of the residence time of the EE forager by 17.6% and by 408.33% for the LE forager (Table 4).
). Increasing the average travel time by 4000% resulted in an increase of the residence time of the EE forager by 17.6% and by 408.33% for the LE forager (Table 4).
3.2. Model Validation
Simulation models are not right or wrong, they are simply more or less useful in ordering current information, identifying patterns and guiding future research inquires [26]. To assess the accuracy and usefulness of our model we compared SeekSMART outputs with data obtained from field studies.
Previous research on elk foraging behavior [27-30] indicates that an average elk during its 24 h activity should forage for 8 to 12 h (depending on its reproductive condition). Similar findings were reported for other cervids [31]. This total foraging time should be divided between 9.2 to 9.7 foraging bouts and result in cumulative consumption of dry matter in the range of 6.99 to 12.53 kg of forage (on average 9.18 kg [27]).
In the SeekSMART’s validation run, the lower limit of the consumption range (6.99 kg) was reached by the virtual elk using an MVT foraging strategy at 9.1 h of the simulation (Figure 3). The animal needed 12 h to consume 9.18 kg of forage. At Total Time = 19.6 h, the virtual animal consumed 12.53 kg reaching the upper limit of daily consumption [27]. Assuming that the animal’s gut is full at 9.18 kg, the virtual forager reached this condition at 12.9 h and required a period of rest to be able to continue foraging. Due to a digestion and rumination processes that occur when not grazing, cumulative consumption of the virtual elk was different from gut fill and reached the value of 9.18 kg at 12 h. In validating the model, we assumed that the forager could multitask [2] and digest the consumed food when traveling from one patch to another.
The forager in the validation run visited 11 patches, however, travel times to reach patches 1, 2, 5, 6, 7 were 0.0 h. Therefore, foraging in patches 1 and 2, as well as in 5, 6 and 7 could be interpreted as foraging within one patch because the forager did not interrupt its foraging bouts. The number of foraging bouts during the 24 h period for the virtual elk was 9.1 (Figure 3).
Therefore, in the validation run, the forager performed within the range of values obtained in field research. When the default settings were used to describe the forager and the landscape, SeekSMART produced realistic results that closely reflected actual field observations.

Figure 3. Behavior of the virtual elk in the validation run. Foraging pauses were caused by the gut fill reaching 9.18 kg, which, due to rumination and digestion when not foraging, was reached later than cumulative consumption of the same value.
4. DISCUSSION
Our results indicate that for animals using the MVT as a foraging strategy, patch residence time (Tr) depends on the distribution of patches of resources, their quality, and foraging efficiency of the forager. The outputs also indicate that the efficiency of the forager (slope of the functional response curve) in combination with travel times and quality of patches produces specific patterns of behavior. It reveals an interesting finding that some foragers are immune to changes in travel times. In other words, changing travel times (Tt) do not affect patch residence times (Tr) of these foragers.
One would assume that in hypothetical habitat 1 with sparsely distributed patches, foragers would stay longer within an average patch than in habitat 2 characterized by the same patches (the same forage biomass in any given patch) where the average travel time between patches is shorter. This is the common interpretation of the MVT. Our findings show that whereas this is true for most foragers, it does not apply to very efficient foragers. With the increasing efficiency of foragers, their residence times (Tr) are less affected by travel times (Tt) between patches.
There are several factors that may affect foraging efficiency. It may be the type of forage (for example graminoids versus foliage) and seasonal changes in its structure and composition; it may be the age of the forager (e.g., mouth size, neck length, muscle weight, etc.). All these factors affect the efficiency of consumption and thus indirectly affect patch residence times. Therefore, an elk using the MVT foraging strategy and feeding on patches of grass in spring will most likely have “spring” residence times different than “fall” residence times in the same habitat (the same distribution and biomass of patches). The same principle would apply to other species feeding in their habitats.
If travel between patches is short, then very efficient foragers should stay in the patch longer than medium efficiency foragers, and the low efficiency foragers should stay in the patch for the shortest time. These results are in agreement with the common understanding of the consequences of the MVT: the intake rates of very efficient foragers at low biomass of forage are not much lower than their intake rates at a higher amount of forage. This allows the efficient foragers to exploit patches at a rate not much lower than the maximum intake rate even if patch biomass density is low. Therefore, a very efficient forager (i.e., having a very steep functional response curve) benefits from staying in a patch for a longer time than a forager of lower efficiency. In contrast, the intake rate of an inefficient forager, (i.e., those having a gentle slope of the functional response curve) is affected by the decreasing biomass in a patch soon after initiating the foraging bout within a patch. Therefore, it is more beneficial for this forager to move to a new patch if travel between patches is short.
This situation is reversed in a landscape where travel between patches requires more time. Although most foragers in this case should stay longer in an average patch than in a landscape with shorter travel times, this change is most pronounced for low efficiency foragers. When travel time becomes significant, low efficiency foragers should stay longer in a patch and continue to exploit the current patch, whereas a highly efficient forager should leave the patch earlier and use its high potential in exploiting resources at a new patch.
It is apparent that highly efficient foragers are more resistant to changing travel times than foragers of low efficiency. For a very efficient forager, travel time had little effect on patch residence time. For example, the EE Forager 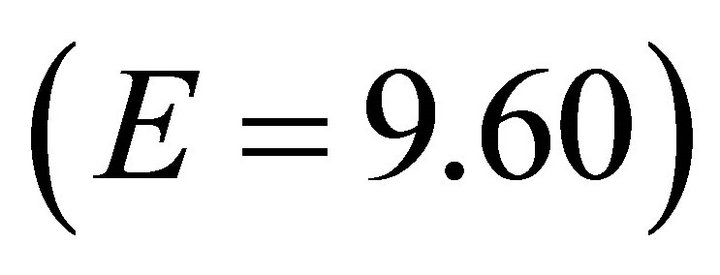 in Landscape CT1, according to the MVT, should stay within the patch for 2.6 h and for 2.85 h in Landscape CT5. This is a 9.6 % increase in Tr with a 40 fold increase in travel time. For the same increase in Tt the increase in Tr for a low efficiency (LE) forager was 323% (an increase from 1.3 h to 4.2 h). It can be shown that for the extremely efficient foragers, applying the MVT, Tt should not affect Tr. In the simulations, extremely efficient foragers (E = 9.60) had almost the same Tr for each landscape type (Landscape C: 2.6-2.85h, mean 2.77 h; Landscape B: 1.65-1.9h, mean 1.84 h; Landscape A: 0.85-1.00, mean 0.94 h) (Figure 4).
in Landscape CT1, according to the MVT, should stay within the patch for 2.6 h and for 2.85 h in Landscape CT5. This is a 9.6 % increase in Tr with a 40 fold increase in travel time. For the same increase in Tt the increase in Tr for a low efficiency (LE) forager was 323% (an increase from 1.3 h to 4.2 h). It can be shown that for the extremely efficient foragers, applying the MVT, Tt should not affect Tr. In the simulations, extremely efficient foragers (E = 9.60) had almost the same Tr for each landscape type (Landscape C: 2.6-2.85h, mean 2.77 h; Landscape B: 1.65-1.9h, mean 1.84 h; Landscape A: 0.85-1.00, mean 0.94 h) (Figure 4).
We argue that if a forager is extremely efficient in consuming resources, its Tr should not be affected by the distances between patches. Such a forager can be called a perfect forager. Tr of the prefect forager is affected by the biomass of forage in the patch and it is the only factor that affects the Tr of the perfect forager. Therefore, if a forager does not adjust its patch Tr across a spectrum of landscapes with different average travel times it does not necessarily mean that the forager is not using the MVT. It simply is a perfect forager. Its main characteristic is its ability to forage with the same rate at most densities of the resource. Therefore, a perfect forager is a forager that stays and feeds in the average patch until all the resources are fully consumed. A caterpillar feeding on a leaf of a plant until the leaf is completely consumed [32, 33] is an example of a perfect forager. It feeds on the same leaf with a constant intake rate until the leaf is almost completely consumed or until all edible parts of the leaf are completely consumed. The caterpillar next travels to a new leaf (patch). It is well known that caterpillars would sometimes stop foraging and stay on the same leaf to resume feeding later [32,34]. They do not need to move to a new leaf even if a large proportion of the current leaf has been consumed. One can observe a similar behavioral pattern in seed eating birds feeding on food
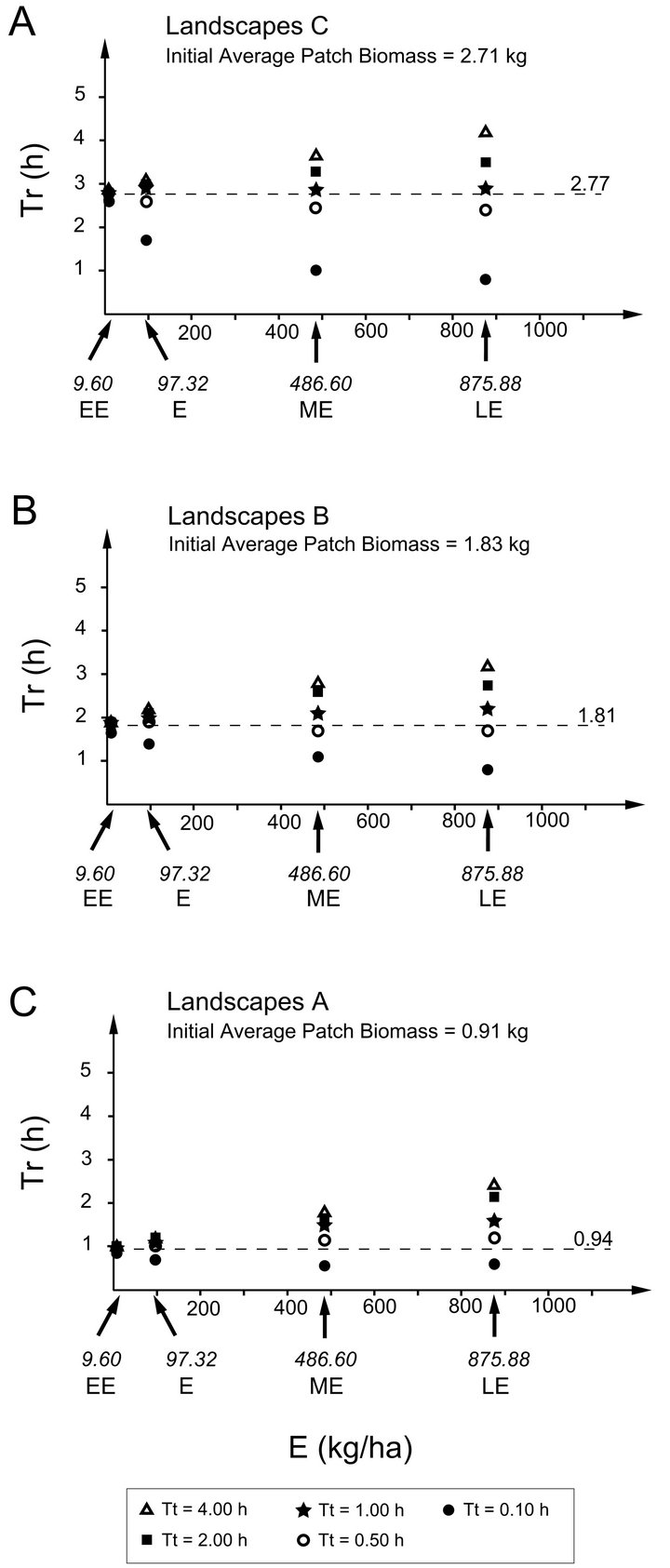
Figure 4. Patch residence times (Tr) obtained by applying the MVT to four types of foragers: EE, E, ME, and LE with five different average travel times (Tt) between patches (0.10, 0.50, 1.00, 2.00 and 4.00 h) in landscapes of types C, B and A. Dashed lines indicate the mean Tr for the EE forager in a given landscape type.
provided in feeders. Many non-breeding birds usually perch next to a feeder and continue to feed from the same feeder until all seeds in a given feeder (patch) are fully consumed. Animals that feed in environments with clumpy distribution of resources, and able to feed within the same patch without reducing their instantaneous intake rate, are examples of perfect foragers.
It is the ratio of the foraging efficiency  and the maximum intake
and the maximum intake 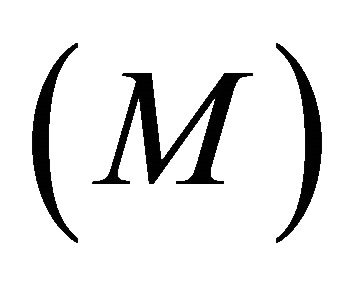 that defines the slope of the functional response curve and the efficiency of the forager. We call this ratio foraging coefficient
that defines the slope of the functional response curve and the efficiency of the forager. We call this ratio foraging coefficient 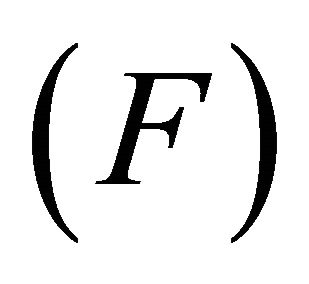 and express it as a quotient of E and M:
and express it as a quotient of E and M:
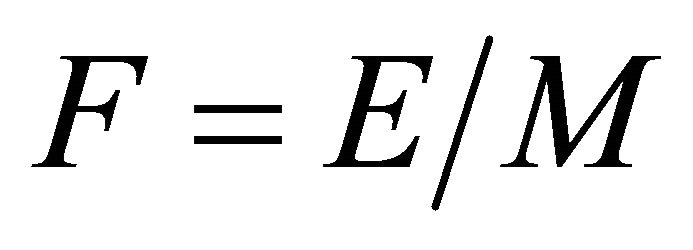 (2)
(2)
A perfect forager is a forager whose foraging coefficient F is close to 0. In other words,
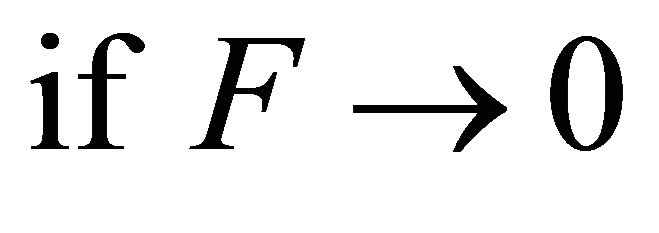 (3)
(3)
then a forager is a perfect forager and its Tr in a patch of resources is not affected by the distances between patches of resources distributed across the landscape (Figure 5). Regardless of travel time, its patch residence time is always 2.80 h. Its foraging coefficient F is 0.00104. The value of the foraging coefficient of the hypothetical caterpillar would be similar.

Figure 5. (A) The functional response curve (FRC) of the perfect forager in landscape C; and (B) its gain curves and associated patch residence times (Tr = 2.80 h) in landscapes CT1 (1) and CT5 (2) indicated with dashed lines.
The forage consumed from an average patch as a function of Tr (gain function, Figure 5) of a perfect forager, resulting from a very steep functional response curve, is close to a linear function. This is supported by empirical data and research on roe deer (Capreolus capreolus) feeding in browse patches, where linear gain functions were observed [35]. The idea of linear gain functions being typical for browsers is further supported by the very steep slope of the functional response curve observed for a browser [26] and similar to that associated with perfect foragers.
There are other field data obtained in research focused on ungulates that support the perfect forager theorem. Examination of the mechanisms responsible for forage intake rates of mammalian herbivores [36] reveals that intakes of mammalian browsers are often poorly related to food biomass. The models constructed to illustrate intake rates of caribou (Rangifer tarandus), black-tailed deer and moose (Alces alces) suggest relatively constant intake rates across a wide range of plant biomass and a sharp drop in these rates when the plant biomass is near 0 [37-39]. This is a pattern exhibited by the perfect forager (Figure 5).
There are examples of field data for carnivores that suggest perfect foragers among large predators. Kill rates of wolves (Canis lupus) preying on a rapidly growing moose population in the east-central Yukon [40] were higher than those predicted at low moose densities and described by the type II functional response of wolves according to the following equation:
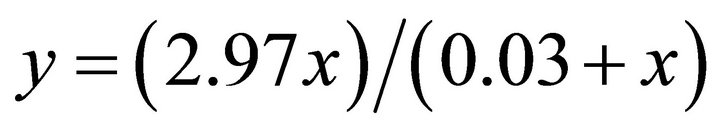 where x is moose density. Based on the values provided in the above equation [40] the foraging coefficient (F) can be calculated as
where x is moose density. Based on the values provided in the above equation [40] the foraging coefficient (F) can be calculated as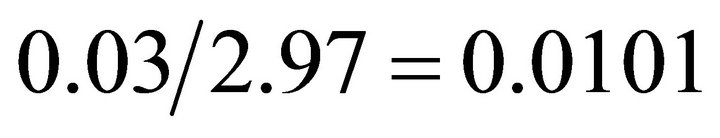 . This indicates a perfect forager.
. This indicates a perfect forager.
A careful analysis of the outputs of our research reveals (Figure 4) a striking similarity between the initial average patch biomasses and the obtained mean patch residence times for the EE foragers (which are close to perfect foragers). In Landscapes of type C, the initial average patch biomass was 2710 grams or 2.71 kg and the mean patch residence time ![]() for the EE forager was 2.77 h. In Landscapes of type B and A, these values were 1.83 kg - 1.84 h and 0.91 - 0.94 h respectively. This suggests that for a perfect forager in the landscapes that we created, the quotient of initial biomass in a patch
for the EE forager was 2.77 h. In Landscapes of type B and A, these values were 1.83 kg - 1.84 h and 0.91 - 0.94 h respectively. This suggests that for a perfect forager in the landscapes that we created, the quotient of initial biomass in a patch  and residence time
and residence time ![]() calculated according to the MVT should be close to 1. This value could be different depending on the species, its habitat, forage type and associated units of measurement. However, it is the relationship between the average patch biomass
calculated according to the MVT should be close to 1. This value could be different depending on the species, its habitat, forage type and associated units of measurement. However, it is the relationship between the average patch biomass  and the residence time
and the residence time ![]() that is critical. Assuming that
that is critical. Assuming that
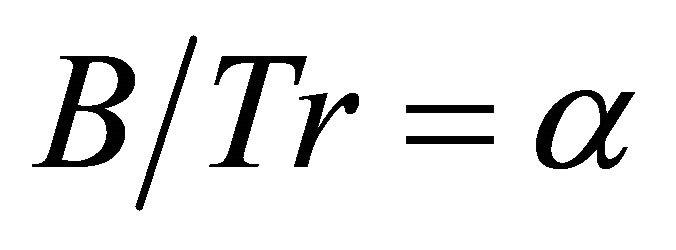 (4)
(4)
then, α is a constant value for a perfect forager.
Analysis of the research findings presented in this paper suggest that for a given landscape (average patch biomass B) there is only one average travel time ![]() such that for this specific average Tt, the residence time
such that for this specific average Tt, the residence time ![]() for all types of foragers is the same (Figure 6). Therefore, for this specific average Tt, the value of α will be the same for any forager. If for a given average travel time:
for all types of foragers is the same (Figure 6). Therefore, for this specific average Tt, the value of α will be the same for any forager. If for a given average travel time:
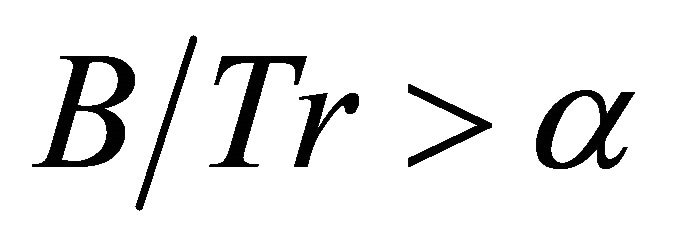 (5)
(5)
then low efficiency foragers will stay in a patch for a shorter time than efficient foragers, and if
 (6)
(6)
then the low efficiency forager will stay in a patch longer than the efficient forager in the same patch.
In the landscapes of type C, the average travel time for which Tr of all foragers is the same is between 0.5 and 1.0 h and certainly very close to 1.0 h. It can be said that the residence times of different foragers in any given habitat with patches of the same quality, but with variable distances between patches, rotate around α that becomes a foragers’ hub in a given habitat (Figure 6).
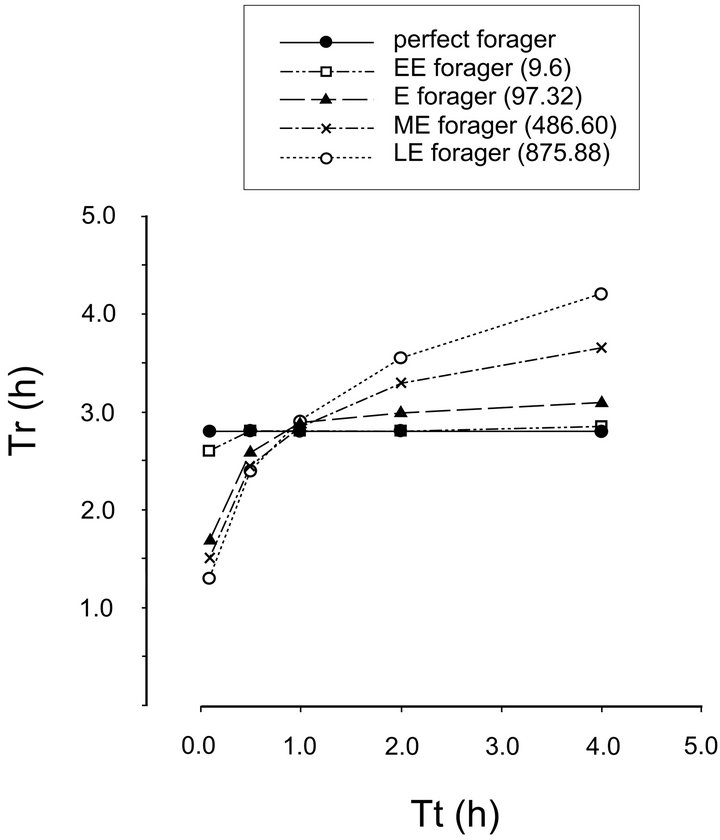
Figure 6. Illustration of α—the foragers’ hub. The residence times (Tr) of different foragers in any given habitat with patches of the same average quality, but with increasing average distances between patches rotate around α that becomes a foragers’ hub in a given habitat.
Our findings suggest that each habitat has its foragers’ hub (α) and any forager feeding in this habitat can be described in relation to the hub (α). This is supported by field observations of feeding behaviors of mule deer (Odocoileus hemionus) and blue duikers (Cephalophusmonticola) and an observed pattern [36] that represents a small portion of the relationship described in Figure 6. Looking at more foragers with more diverse efficiencies and feeding in the same habitats [36], but with a wider spectrum of travel times between patches would, according to the principle of the perfect forager and for ager’s hub, produce the remaining sections of the hub (α) illustrated in Figure 6.
The concept of forager’s hub could be a useful ecological indicator. The position of a given forager (its α1) in relation to the hub (α) would indicate the efficiency of the individual forager. Plotting the values of α for the individual animals in a population would illustrate the variability in that population (efficient and less efficient foragers) which could indicate potential competition for resources, unequal distribution of resources, and therefore, stability of the population [41].
5. CONCLUSIONS
If a foraging animal does not seem to be following MVT strategies (patch residence time ![]() does not change with increasing travel time even though the quality of patches remains constant), it may still use an MVT foraging strategy based on its efficiency in utilizing resources in individual patches. Each perfect forager should stay for the same time in an average patch regardless of travel times. Therefore, patch residence times cannot be used as the only criteria to assess whether the animal is behaving according to the MVT. If a forager’s Tr does not change with changing travel times, it does not necessarily mean that the animal is forced to abandon the MVT due to its interactions with other individuals of the same or other species (mating season, predation risk, etc.) as was proposed [10]. We have shown that very efficient foragers and perfect foragers should not change their patch residence times even if the distribution of patches across the landscape changes dramatically.
does not change with increasing travel time even though the quality of patches remains constant), it may still use an MVT foraging strategy based on its efficiency in utilizing resources in individual patches. Each perfect forager should stay for the same time in an average patch regardless of travel times. Therefore, patch residence times cannot be used as the only criteria to assess whether the animal is behaving according to the MVT. If a forager’s Tr does not change with changing travel times, it does not necessarily mean that the animal is forced to abandon the MVT due to its interactions with other individuals of the same or other species (mating season, predation risk, etc.) as was proposed [10]. We have shown that very efficient foragers and perfect foragers should not change their patch residence times even if the distribution of patches across the landscape changes dramatically.
In this paper we examined the behaviors of different foragers and the relationships between these foragers on a small spatial and temporal scale. A question remains open how these relationships among foragers is reflected on a longer temporal and larger spatial scales. What are the consequences of the forager’s choices over a longer period of time (e.g. several days)? These important questions certainly require more research in a simulation setting where environmental noise can be eliminated to fully understand the consequences of the MVT in relation to other foraging strategies.
6. ACKNOWLEDGEMENTS
We would like to thank Lee Foote, G. Peter Kershaw, Scott Nielsen and Michael Gillingham for their helpful comments on this manuscript.
![]()
![]()
REFERENCES
- Charnov, E.L. (1976) Optimal foraging, the marginal value theorem. Theoretical Population Biology, 9, 129- 136. doi:10.1016/0040-5809(76)90040-X
- Best, L. and Bierzychudek, P. (1982) Pollinator foraging on foxglove (Digitalis purpurea): A test of a new model. Evolution, 36, 70-79. doi:10.2307/2407968
- Bonser, R., Wright, P.J., Bament, S. and Chukwu, U.O., (2001) Optimal patch use by foraging workers of Lasius fuliginosus, L. Niger and Myrmica ruginodis. Ecological Entomology, 23, 15-21. doi:10.1046/j.1365-2311.1998.00103.x
- Jiang, Z. and Hudson, R.J. (1993) Optimal grazing of wapiti (Cervus elaphus) on grassland: Patch and feeding station departure rules. Evolutionary Ecology, 7, 488-498. doi:10.1007/BF01237643
- Laca, E.A., Ungar, E.D. and Demment, M.W. (1994) Mechanisms of handling time and intake rate of a large mammalian grazer. Applied Animal Behaviour Science, 39, 3-19. doi:10.1016/0168-1591(94)90011-6
- Pyke, G.H. (1978) Optimal foraging in bumblebees and coevolution with their plants. Oecologia, 36, 281-293. doi:10.1007/BF00348054
- Wajnberg, E., Fauvergue, X. and Pons, O. (2000) Patch leaving decision rules and the Marginal Value Theorem: An experimental analysis and a simulation model. Behavioral Ecology, 11, 577-586. doi:10.1093/beheco/11.6.577
- Carmel, Y. and Ben-Haim, Y. (2005) Info-gap robustsatisficing model of foraging behavior: Do foragers optimize or satisfice? American Naturalist, 166, 633-641. doi:10.1086/491691
- Moen, R., Cohen, Y. and Pastor, J. (1998) Linking moose population and plant growth models with a moose energetics model. Ecosystems, 1, 52-63. doi:10.1007/s100219900005
- Nonacs, P. (2001) State dependent behavior and the Marginal Value Theorem. Behavioral Ecology, 12, 71-83. doi:10.1093/oxfordjournals.beheco.a000381
- Alonso, J.C., Alonso, J.A., Bautista, L.M. and MunozPolido, R. (1995) Patch use in cranes: A field test of optimal foraging predictions. Animal Behavior, 49, 1367- 1379. doi:10.1006/anbe.1995.0167
- Fortin, D., Boyce, M.S., Merrill, E.H. and Fryxell, J.M. (2004) Foraging costs of vigilance in large mammalian herbivores. Oikos, 107, 172-180. doi:10.1111/j.0030-1299.2004.12976.x
- Hansen, J. (1987) Tests of optimal foraging using an operant analogue. In: Kamil, A.C., Krebs, J.R. and Pulliam, H.R., Eds., Foraging Behavior, Plenum Press, New York, 335-362. doi:10.1007/978-1-4613-1839-2_10
- Hanson, J. and Green, L. (1989) Foraging decisions: Patch choice and exploitation by pigeons. Animal Behaviour, 37, 968-986. doi:10.1016/0003-3472(89)90141-3
- Howell, D.J. and Hartl, D.L. (1980) Optimal foraging in glossophagine bats: When to give up. American Naturalist, 115, 696-704. doi:10.1086/283592
- Kamil, A.C., Misthal, R.L. and Stephens, D.W. (1993) Failure of simple optimal foraging models to predict residence time when patch quality is uncertain. Behavioral Ecology, 44, 350-363. doi:10.1093/beheco/4.4.350
- Schluter, D. (1982) Optimal foraging in bats: Some comments. American Naturalist, 119, 121-125. doi:10.1086/283896
- Isee Systems (2008). http://www.iseesystems.com
- Weclaw, P. (2010) Optimal use of resources: Classic foraging theory, satisficing and smart foraging—Modelling foraging behaviors of elk. PhD Thesis, University of Alberta, Edmonton, 202.
- Holling, C.S. (1959) The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Canadian Entomologist, 91, 293- 320. doi:10.4039/Ent91293-5
- Fryxell, J.M., Wilmshurst, J.F. and Sinclair, A.R.E. (2004) Predictive models of movement by serengeti grazers. Ecology, 85, 2429-2435. doi:10.1890/04-0147
- Hudson, R.J. and Watkins, W.G. (1986) Foraging rates of wapiti on green and cured pastures. Canadian Journal of Zoology, 64, 1705-1708. doi:10.1139/z86-257
- Wickstrom, M.L., Robbins, C.T., Hanley, T.A., Spalinger, D.E. and Parish, S.M. (1984) Food intake and foraging energetics of elk and mule deer. Journal of Wildlife Management, 48, 1285-1301. doi:10.2307/3801789
- Owen-Smith, N. (2002) A metaphysiological modelling approach to stability in herbivore-vegetation systems. Ecological Modelling, 149, 153-178. doi:10.1016/S0304-3800(01)00521-X
- Clutton-Brock, T.H., Iason, G.R., Albon, S.D. and Guinness, F.E. (1982) Effects of lactation on feeding behaviour and habitat use in wild red deer hinds (Cervus elaphus, Rhum). Journal of Zoology, 198, 227-236. doi:10.1111/j.1469-7998.1982.tb02072.x
- Hudson, R.J. and White, R.G. (1985) Bioenergetics of Wild Herbivores, CRC Press, Inc., Florida.
- Gedir, J.V. and Hudson, R.J. (2000) Seasonal foraging behavioural compensation in reproductive wapiti hinds (Cervus elaphus canadensis). Applied Animal Behaviour Science, 67, 137-150. doi:10.1016/S0168-1591(99)00117-3
- Gates, C.C. and Hudson, R.J. (1983) Foraging behaviour of wapiti in a boreal forest enclosure (Cervus elaphus nelsoni, Alberta). Naturaliste Canadien, 110, 197-206.
- Gedir, J.V. and Hudson, R.J. (2000) Estimating dry matter digestibility and intake in wapiti (Cervus elaphus canadensis) using the double n-alkane ratio technique. Small Ruminant Research, 36, 57-62. doi:10.1016/S0921-4488(99)00114-5
- Heydon, M.J., Loudon, A.S.I., Milne, J.A. and Brinklow, B.R. (1992) Influence of plane of nutrition on seasonal changes in food intake and reproduction of grazing red deer. In: Brown, R.D., Ed., The Biology of Deer, Springer-Verlag, New York, 279-284. doi:10.1007/978-1-4612-2782-3_62
- Gillingham, M.P., Parker, K.L. and Hanley, T.A. (1997) Forage intake by large herbivores in a natural environment: Bout dynamics. Canadian Journal of Zoology, 75, 1118-1128. doi:10.1139/z97-134
- Heinrich, B. (1979) Foraging strategies of caterpillars— Leaf damage and possible predator avoidance strategies. Oecologia, 42, 325-337.
- Karban, R. (1987) Effects of clonal variation of the host plant, interspecific competition, and climate on the population size of a folivorous thrips. Oecologia, 74, 298-303. doi:10.1007/BF00379373
- Heinrich, B. (1993) How avian predators constrain caterpillar foraging. In: Stamp, N.E. and Casey, T.M., Eds., Caterpillars. Ecological and Evolutionary Constraints on Foraging, Chapman and Hall, New York, 224-247.
- Illius, A.W., Duncan, P., Richard, C. and Mesochina, P. (2002) Mechanisms of functional response and resource exploitation in browsing roe deer. Journal of Animal Ecology, 71, 723-734. doi:10.1046/j.1365-2656.2002.00643.x
- Searle, K.R., Hobbs, N.T. and Shipley, L.A. (2005) Should I stay or should I go? Patch departure decisions by herbivores at multiple scales. Oikos, 111, 417-424. doi:10.1111/j.0030-1299.2005.13918.x
- Spalinger, D.E. and Hobbs, N.T. (1992) Mechanisms of foraging in mammalian herbivores: New models of functional response. American Naturalist, 140, 325-348. doi:10.1086/285415
- Trudell, J. and White, R.G. (1981) The effect of forage structure and availability on food intake, biting rate, bite size and daily eating time of reindeer. Journal of Applied Ecology, 18, 63-81. doi:10.2307/2402479
- Risenhoover, K.L. and Maass, S.A. (1987) The influence of moose on the composition and structure of Isle Royale forests. Canadian Journal of Forest Research, 17, 357- 364. doi:10.1139/x87-062
- Hayes, R.D. and Harestad, A.S. (2000) Wolf functional response and regulation of moose in the Yukon. Canadian Journal of Zoology, 78, 60-66. doi:10.1139/z99-188
- Lomnicki, A. (1978) Individual differences between animals and natural regulation of their numbers. Journal of Animal Ecology, 47, 461-475. doi:10.2307/3794

