Journal of Quantum Information Science
Vol.4 No.1(2014), Article ID:43872,11 pages DOI:10.4236/jqis.2014.41007
Some Features on Entropy Squeezing for Two-Level System with a New Nonlinear Coherent State
Salama I. Ali1, Sayed Abdel-Khalek2
1Mathematics Department, Faculty of Science, Al-Azher University, Cairo, Egypt
2Mathematics Department, Faculty of Science, Sohag University, Sohag, Egypt
Email: salama5laser@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 13 January 2014; revised 22 February 2014; accepted 12 March 2014
ABSTRACT
Entropy squeezing is an important feature in performing different tasks in quantum information processing such as quantum cryptography and superdense coding. These quantum information tasks depend on finding the states in which squeezing can be created. In this article, a new feature on entropy squeezing for a two level system with a class of nonlinear coherent state (NCS) is observed. An interesting result on the comparison between the coherent state (CS) and NCS is explored. The influence of the Lamb-Dick parameter in both absence and presence of the Kerr medium is examined. A rich feature of entropy squeezing in the case of NCS, which is observed to describe the motion of the trapped ion, has been obtained.
Keywords:Entropy Squeezing; Kerr-Like Medium; Nonlinear Coherent State

1. Introduction
It is known that quantum entangled state plays an important role in the fields of quantum information theory as well as quantum teleportation and computation. The entropy which automatically includes all moments of the density operator has been shown to be a very useful operational measure of the purity of the quantum state. The most important and interesting work to understand relation between entropy and information was done by Shannon [1] , who introduced the entropy (Shannon entropy) into communications theory. Recently it has been shown that nonlinear coherent states are useful in the description of the motion of a trapped ion and various non-classical properties of such states have also been studied [2] . We note that in Refs [2] and [3] nonlinear coherent states have been defined as the right eigenstate of a generalized annihilation operator 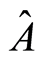 (which emerges from the Hamiltonian describing the dynamics) this is because in the case of nonlinear algebras the commutator
(which emerges from the Hamiltonian describing the dynamics) this is because in the case of nonlinear algebras the commutator  is not a constant or a linear function of the generators of the algebra but nonlinear in the in the generators. As a consequence it is difficult to obtain an explicit form of nonlinear coherent state constructed via the displacement operator technique. The nonlinear coherent state (NCS) was introduced as a new state of the source of the coherent field to describe some of the non-classical properties like squeezing and Sub-Poissnian behavior [4] . There are some previous studies on the entropy squeezing of a two-level atom, such as one photon transition [5] , the nonlinear Kerr medium [6] and degenerate two-photon process [7] . The authors of these papers have focused only on the initial coherent state of the field.
is not a constant or a linear function of the generators of the algebra but nonlinear in the in the generators. As a consequence it is difficult to obtain an explicit form of nonlinear coherent state constructed via the displacement operator technique. The nonlinear coherent state (NCS) was introduced as a new state of the source of the coherent field to describe some of the non-classical properties like squeezing and Sub-Poissnian behavior [4] . There are some previous studies on the entropy squeezing of a two-level atom, such as one photon transition [5] , the nonlinear Kerr medium [6] and degenerate two-photon process [7] . The authors of these papers have focused only on the initial coherent state of the field.
Recently, much attention has been drawn to squeezing in an ensemble of atoms illuminated with light, involving quantum noise and atomic spin polarization measurement [8] , and quantum-controlled few-photon states generated by squeezed atoms [9] . These studies of atomic squeezing are based on the Heisenberg uncertainty relation (HUR), which is regarded as the standard limitation on measurements of quantum fluctuations. HUR is formulated in terms of the variances or standard deviations of the system observable. As an alternative to the HUR, Hirschman [10] studied quantum uncertainty by using quantum entropy theory, and obtained an entropic uncertainty relation for position and momentum which can overcome the limitations of the HUR.
The entropy squeezing and variance squeezing for the entangled sate of a single two-level atom interacting with a single electromagnetic field in a squeezed vacuum a broad bandwidth are studied [11] . Also, the similarities and differences of both reservoirs for the two different models have been explained through some calculations, such as the atomic inversion and the von Neumann entropy. It is to be noted that considering a mode structure plays a role like the squeezing parameter in the case of a squeezed vacuum reservoir. Also, the entropy squeezing of a two-level atom driven by a strong classical field and damped into a modeled reservoir with non-flat density of modes has been investigated [12] . On the other hand, the dynamics of a single atom entropy squeezing of the two-qubit system, in the presence of local squeezed reservoirs, has been discussed. Our aim in the present paper is to investigate the entropy squeezing of a two level atom when the initial state of the field is taken to be NCS and discuss different features of entropy squeezing in the case of NCS. These features are connected with the Lamb-Dick parameter. Here we also examine the influence of a nonlinear medium and the detuning parameter on the squeezing parameter of the atomic operators 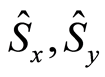 and
and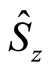 . The organization of the paper is arranged as follows. In Section 2, we present a brief review of the Hamiltonian model and give an exact expression for the density matrix
. The organization of the paper is arranged as follows. In Section 2, we present a brief review of the Hamiltonian model and give an exact expression for the density matrix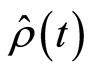 . In Section 3, we employ the density matrix to investigate the properties of the entropy squeezing. Finally, we give our discussion in Section 4.
. In Section 3, we employ the density matrix to investigate the properties of the entropy squeezing. Finally, we give our discussion in Section 4.
2. Dynamics of One Photon JCM
In this paper, we focus our attention to a quantum optical model, where a single two-level atom via one photon process, interacts with a single quantized cavity mode of the radiation field. Then the Hamiltonian of the above system of interest may be written as
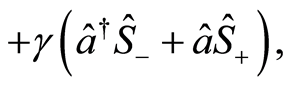
 (1)
(1)
where  is the field frequency,
is the field frequency, 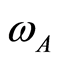 is the atomic frequency,
is the atomic frequency,  and
and 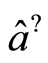 are the annihilation and the creation operators for the mode of the cavity field satisfying
are the annihilation and the creation operators for the mode of the cavity field satisfying  and
and  and
and 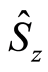 are the atomic spin operators defined by
are the atomic spin operators defined by
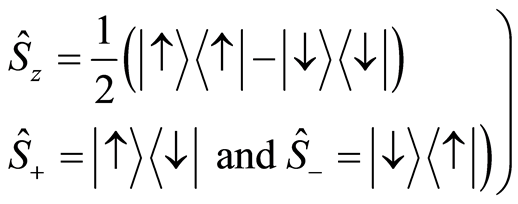 (2)
(2)
We denoted by  and
and 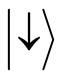 the upper and lower states of the atom, respectively and
the upper and lower states of the atom, respectively and 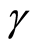 is the effective coupling constant. Also, we denoted by
is the effective coupling constant. Also, we denoted by 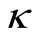 the dispersive part of the third-order nonlinearity of the Kerr-like medium, with the detuning parameter
the dispersive part of the third-order nonlinearity of the Kerr-like medium, with the detuning parameter 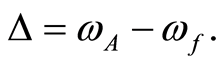 Therefore, we employ the unites of
Therefore, we employ the unites of  The effective Hamiltonian can be written as
The effective Hamiltonian can be written as
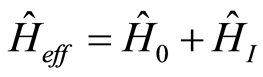
where,
 (3)
(3)
For convenience, we take, 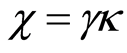 ,
, 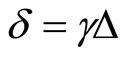 and assume that the atom is initially in the superposition state
and assume that the atom is initially in the superposition state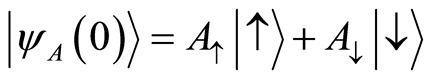 . Also, we assume that the field is initially in the new nonlinear coherent state (NCS),
. Also, we assume that the field is initially in the new nonlinear coherent state (NCS),
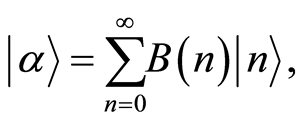 (4)
(4)
where, 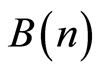 is the distribution function of the NCS. The NCS is defined as
is the distribution function of the NCS. The NCS is defined as 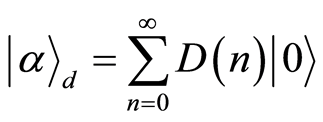 i.e., it is a coherent state (CS) corresponding to the second algebra [13] . One can write
i.e., it is a coherent state (CS) corresponding to the second algebra [13] . One can write 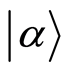 in the following form [4] -[7] [13]
in the following form [4] -[7] [13]
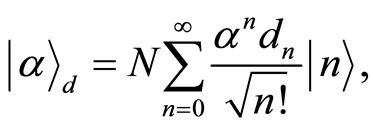
where 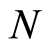 is a normalization constant, which can be determined from the condition
is a normalization constant, which can be determined from the condition 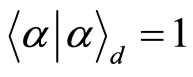 and is given by
and is given by
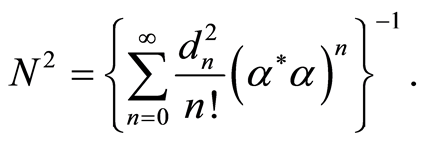
While  and the coefficients
and the coefficients 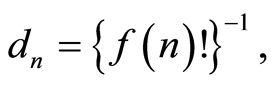 it is clear that for different choices of the nonlinearity function, we shall get different nonlinear coherent states. In the present case we choose a nonlinearity function, which has been used in the description of the motion of a trapped ion [14] .
it is clear that for different choices of the nonlinearity function, we shall get different nonlinear coherent states. In the present case we choose a nonlinearity function, which has been used in the description of the motion of a trapped ion [14] .

where  is known as the Lamb-Dick parameter and
is known as the Lamb-Dick parameter and 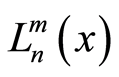 are generalized Lagurre polynomials given by
are generalized Lagurre polynomials given by
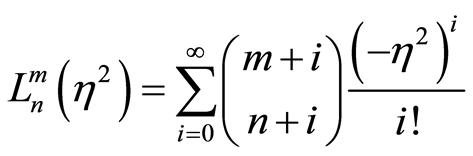 (5)
(5)
Clearly  when
when  and in this case nonlinearity coherent states become the standard coherent states. However, when
and in this case nonlinearity coherent states become the standard coherent states. However, when 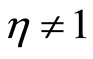 nonlinearity starts developing with degree of depending on the magnitude of
nonlinearity starts developing with degree of depending on the magnitude of 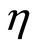 [14] . Then the initial state of the atom-field coupling system reads as
[14] . Then the initial state of the atom-field coupling system reads as
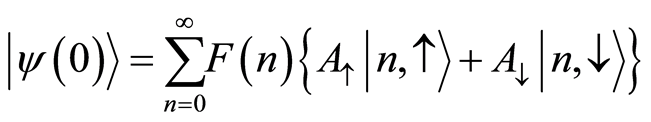 (6)
(6)
where, 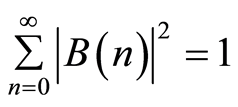 ,
, 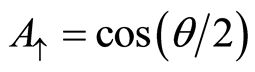 and
and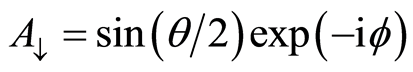 . Here
. Here  denotes the initial coherence of the two-level atom and
denotes the initial coherence of the two-level atom and  is the relative phase between the upper and lower states of the two-level atom. Thus the initial density operator of the system is given by
is the relative phase between the upper and lower states of the two-level atom. Thus the initial density operator of the system is given by  where,
where, 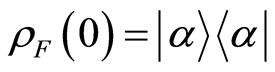 and
and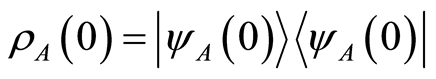 ,
, 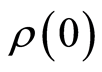 describes the initial values for the field-atom density operator.
describes the initial values for the field-atom density operator.
At any time 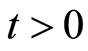 the solution of the Schrödinger equation
the solution of the Schrödinger equation
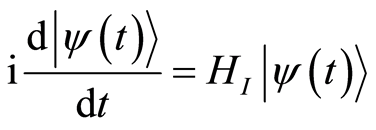 (7)
(7)
for the state vector  with the initial condition (6) is
with the initial condition (6) is
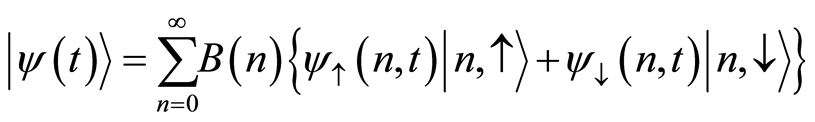 (8)
(8)
and the density matrix of system is
 (9)
(9)
where the coefficient 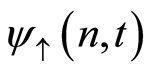 and
and 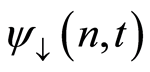 are given by
are given by

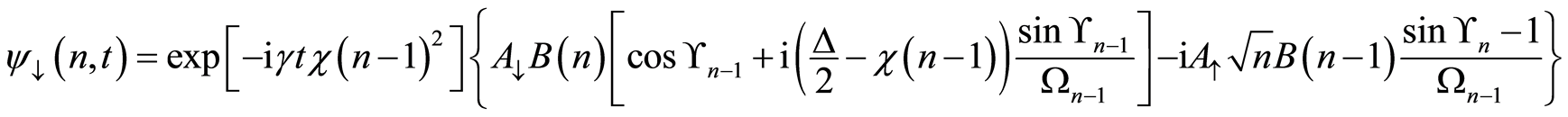 (10)
(10)
where, 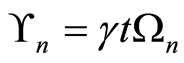 ,
, 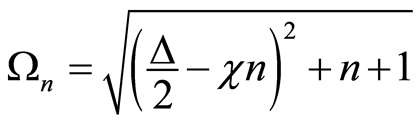 with
with 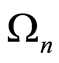 is the Rabi frequency which depends on the detuning parameter and nonlinear medium parameter.
is the Rabi frequency which depends on the detuning parameter and nonlinear medium parameter.
3. Atomic Inversion
We mainly devote the present section to considering the atomic inversion, from which the phenomenon of collapses and revivals can be observed. However, we shall first introduce some expressions for the probability amplitude. The expressions  and
and 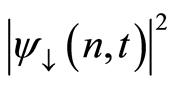 represent the probabilities that at time
represent the probabilities that at time 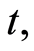 the field has
the field has 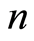 photons present and the atom is in level
photons present and the atom is in level  and
and 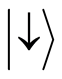 respectively. The probability
respectively. The probability  that there is
that there is 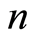 photons in the field at time
photons in the field at time 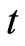 is therefore obtained by taking the trace over the atomic states, i.e.,
is therefore obtained by taking the trace over the atomic states, i.e.,
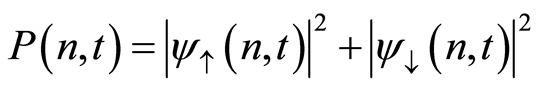 (11)
(11)
where 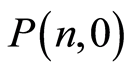 is the probability that there are
is the probability that there are 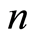 photons present the field at time
photons present the field at time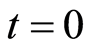 , which is given for a NCS for the field by
, which is given for a NCS for the field by
 (12)
(12)
Another important quantity one may consider is the atomic inversion 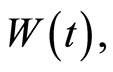 which is related to the probability amplitudes
which is related to the probability amplitudes 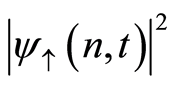 and
and 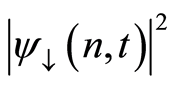 by the expression
by the expression
 (13)
(13)
Thus from Equation (13) and after some rearrangements, we can obtain
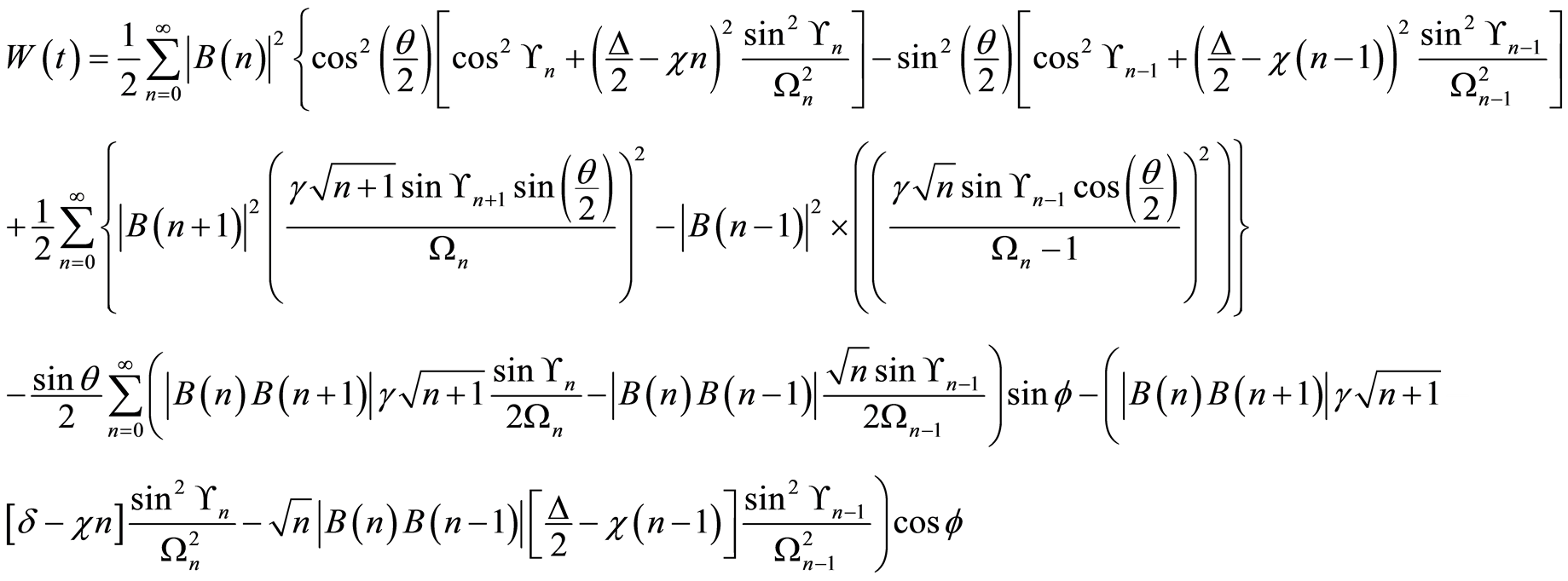 (14)
(14)
4. Entropy Squeezing
In this paper, we use the Heisenberg uncertainty relation (HUR) to study the squeezing information entropy. It has been pointed out that the Heisenberg uncertainty relation (HUR) cannot give sufficient information on the atomic squeezing in some cases [13] . For instance, for a two-level atom, characterized by Pauli operator 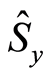
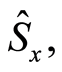 and
and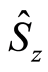 , the uncertainty relation is given by
, the uncertainty relation is given by
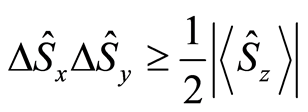
where the Pauli operators 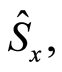
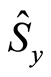 and
and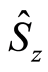 , satisfying the commutation
, satisfying the commutation  and
and 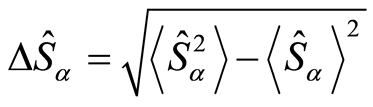 . In this way, the fluctuation in the component
. In this way, the fluctuation in the component  of the atomic dipole is said to be squeezed if
of the atomic dipole is said to be squeezed if  satisfies the condition
satisfies the condition
 (15)
(15)
An optimal entropic uncertainty relation for sets of 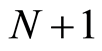 complementary observables with non-degenerate eigenvalues in an even N-dimensional Hilbert space has been recently investigated using quantum entropy theory [5] . It takes the form
complementary observables with non-degenerate eigenvalues in an even N-dimensional Hilbert space has been recently investigated using quantum entropy theory [5] . It takes the form
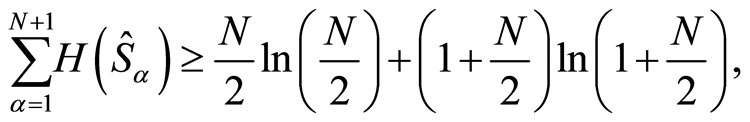 (16)
(16)
where  represents the information entropy of the variable
represents the information entropy of the variable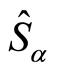 . The aim of this paper is to use entropy uncertainty relation EUR (16) as a general criterion for the squeezing in terms of information entropy for a two-level atom in the Jaynes-Cumming model with one-photon process in a non-linear Kerr medium.
. The aim of this paper is to use entropy uncertainty relation EUR (16) as a general criterion for the squeezing in terms of information entropy for a two-level atom in the Jaynes-Cumming model with one-photon process in a non-linear Kerr medium.
The probability distribution for N possible outcomes of measurements for an arbitrary quantum state of an operators 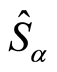 is
is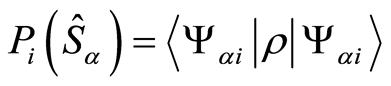 , where
, where 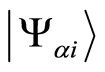 is an eigenvector of the operator
is an eigenvector of the operator 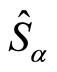 such that
such that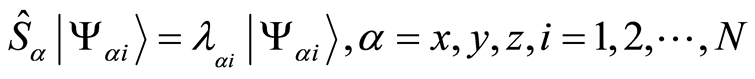 . The corresponding Shannon information entropies are then defined as
. The corresponding Shannon information entropies are then defined as
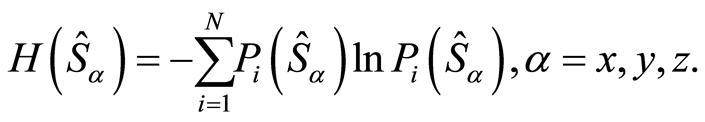 (17)
(17)
To obtain the Shannon information entropies of the atomic operators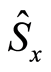 ,
, 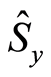 and
and 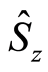 for a two-level atom, with
for a two-level atom, with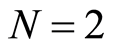 , one can use the reduced atomic density operator
, one can use the reduced atomic density operator , thus we have the following expression,
, thus we have the following expression,
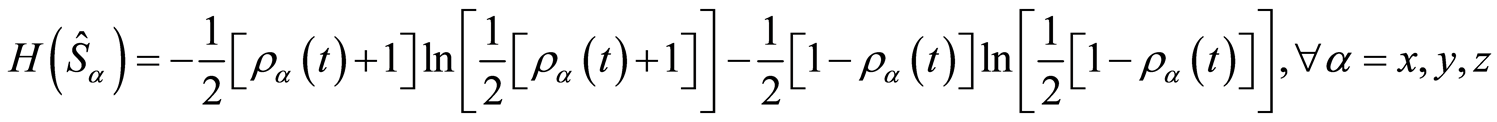
so that
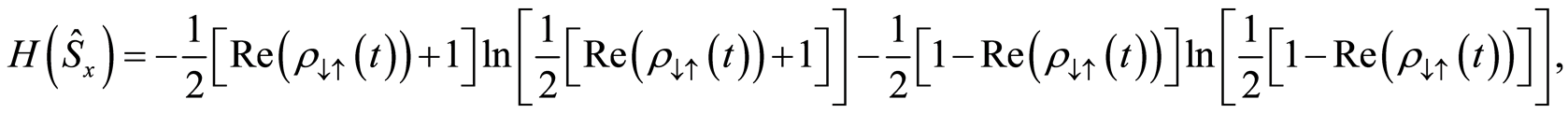 (18)
(18)
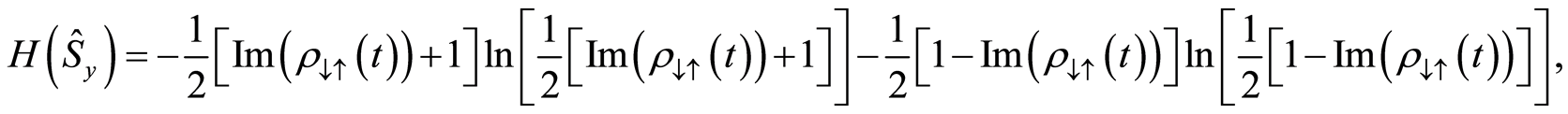 (19)
(19)
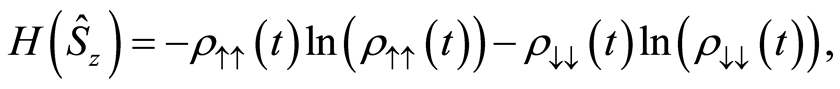 (20)
(20)
where  and
and 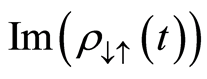 are given by
are given by
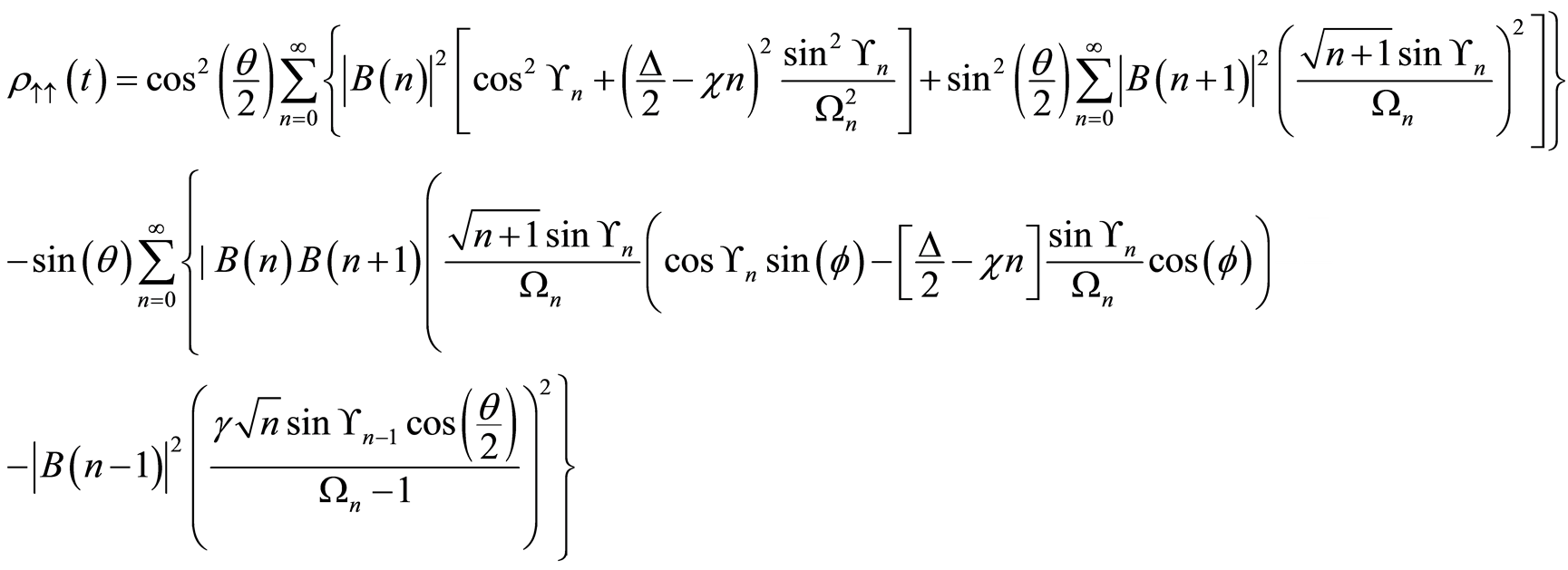 (21)
(21)
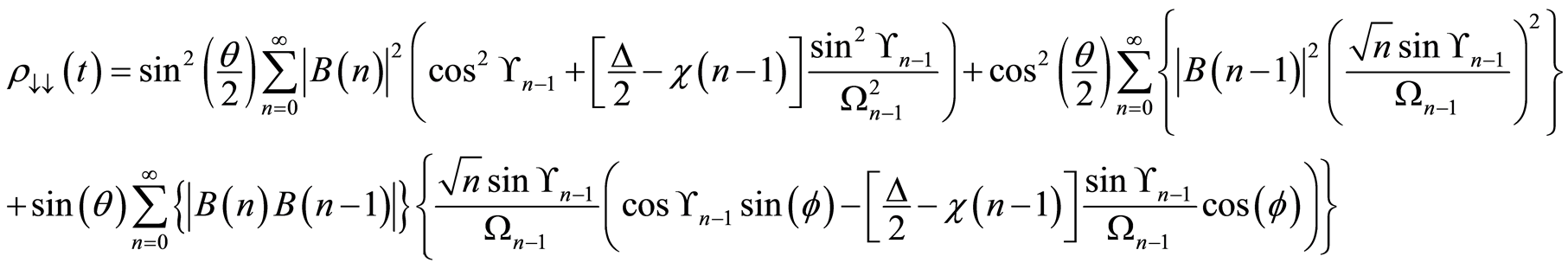 (22)
(22)
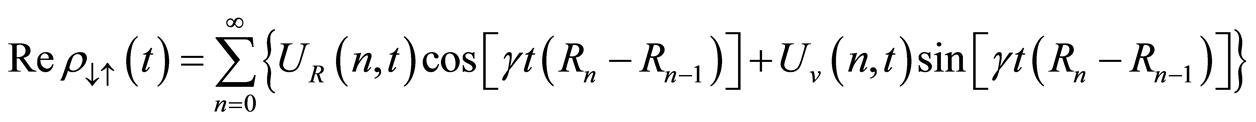 (23)
(23)
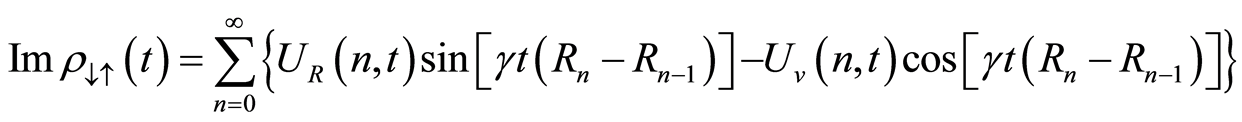 (24)
(24)
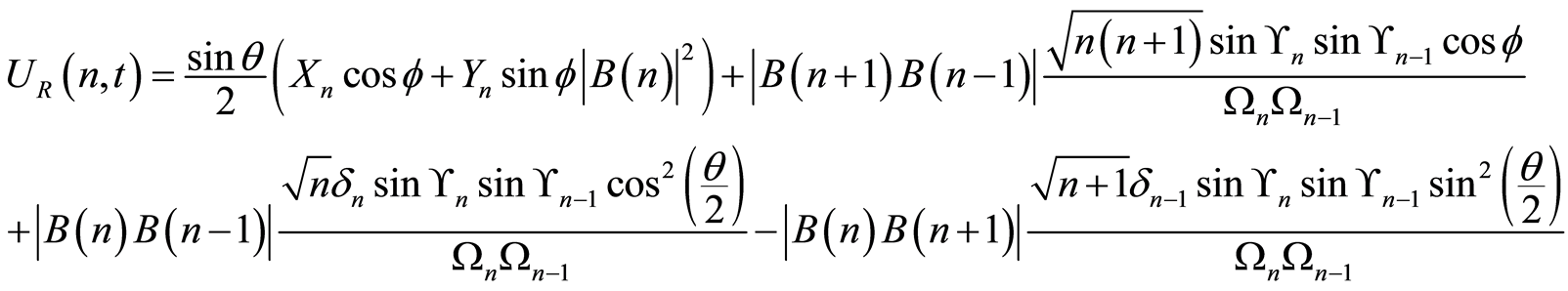 (25)
(25)
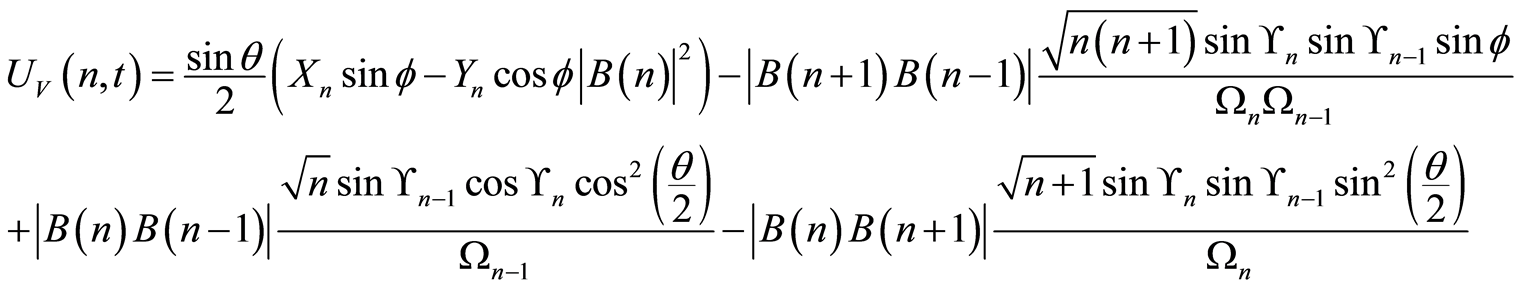 (26)
(26)
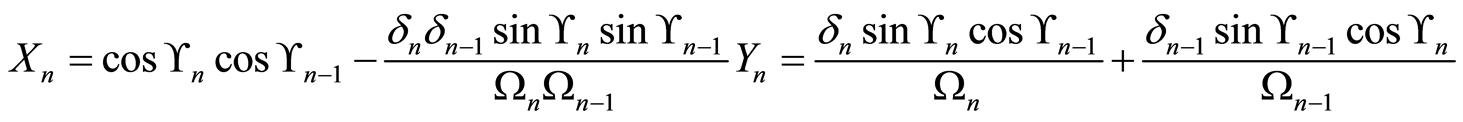 (27)
(27)
Since the uncertainty relation of the entropy can be used as a general criterion for the squeezing of an atom, therefore for a two-level atom. For , we have
, we have 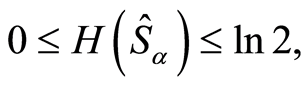 and the Shannon information entropies of the operators
and the Shannon information entropies of the operators 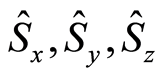 will satisfy the inequality
will satisfy the inequality
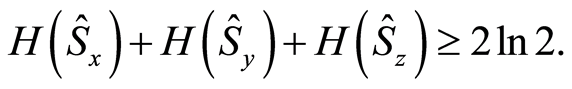 (27)
(27)
In other words, if we define 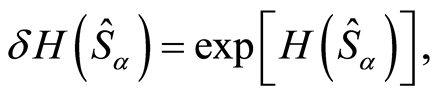 then we can write
then we can write
 (28)
(28)
It is evident that  corresponds to the atom being in a pure state and
corresponds to the atom being in a pure state and 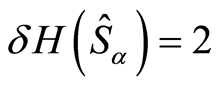 corresponds to the atom being in a mixed state. The EUR (16) shows the impossibility of simultaneously having complete information about the observables
corresponds to the atom being in a mixed state. The EUR (16) shows the impossibility of simultaneously having complete information about the observables 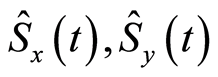 and
and 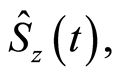 where
where 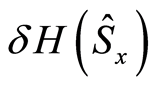 and
and 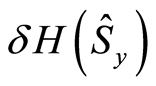 respectively measure the uncertainties of the polarization components
respectively measure the uncertainties of the polarization components 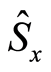 and
and 
Now, we define the squeezing of the atom using EUR (16), named squeezing entropy [5] . The fluctuation of the component  of the atom dipole are said to be “squeezed in entropy” if the information entropy
of the atom dipole are said to be “squeezed in entropy” if the information entropy 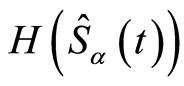 of
of  satisfies the condition
satisfies the condition
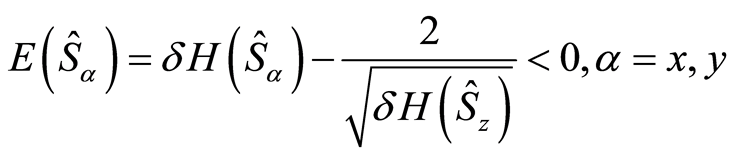 (29)
(29)
n what follows we shall consider the effect of detuning parameter and the nonlinear Kerr like medium on the dynamical behavior of the squeezing entropy of the system under consideration.
5. Numerical Computation
On the basis of the analytical solution presented in the previous section, we shall study numerically the dependence of the 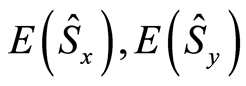 entropy squeezing and the atomic inversion
entropy squeezing and the atomic inversion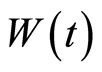 , for various parameters of the one photon model. We recall that time
, for various parameters of the one photon model. We recall that time 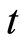 has been scaled; one unit of time is given by the inverse of the coupling constant
has been scaled; one unit of time is given by the inverse of the coupling constant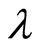 . In all our plots we take
. In all our plots we take 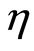 to represent the Lamb-Dicke parameter and the parameter
to represent the Lamb-Dicke parameter and the parameter . For the case of
. For the case of 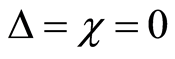 (Figure 1), we investigate the influence of the mean photon number on the entropy squeezing
(Figure 1), we investigate the influence of the mean photon number on the entropy squeezing
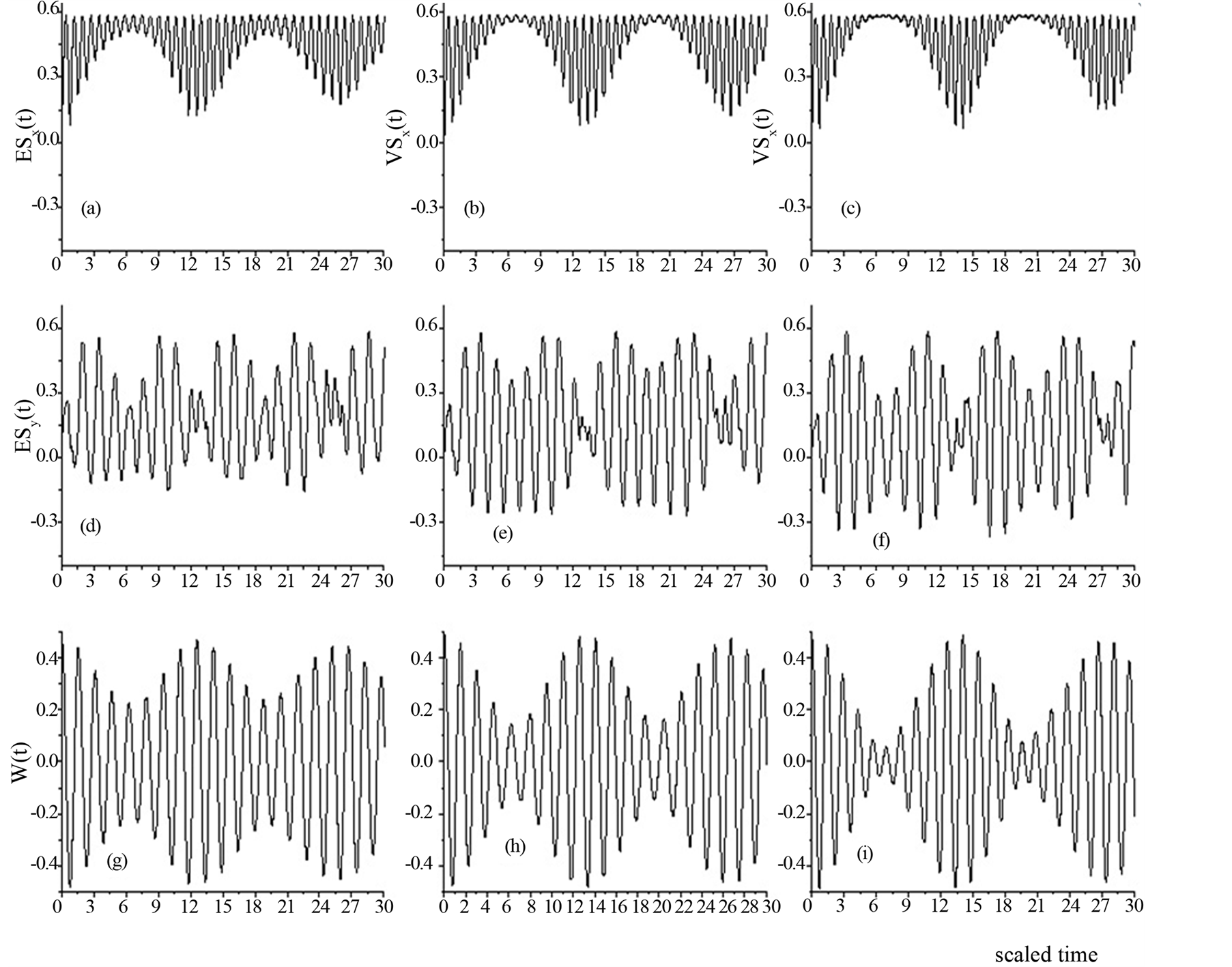
Figure 1. The time evolution of the entropy squeezing factors ,
, 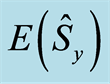 and population inversion
and population inversion  of a two-level atom interacting with a single-mode in the excited state
of a two-level atom interacting with a single-mode in the excited state 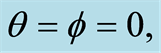 for parameter
for parameter  and with different values of the parameter
and with different values of the parameter 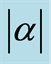 where
where 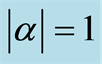 in Figures (a,d,g),
in Figures (a,d,g), 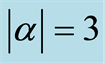 in Figures (b,e,h) and
in Figures (b,e,h) and 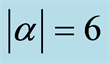 in Figures (c,f,i).
in Figures (c,f,i).
factor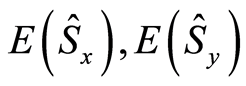 , and population inversion
, and population inversion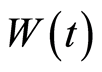 . We notice that no squeezing occurs on the atomic variable
. We notice that no squeezing occurs on the atomic variable 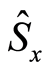 as the parameter increased (see Figures 1(a)-(c)).
as the parameter increased (see Figures 1(a)-(c)).
But Figures 1(d)-(f), present that with increasing the parameter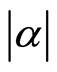 , the entropy squeezing on the atomic variables
, the entropy squeezing on the atomic variables 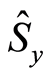 is increased. Also the quantum revival is increased but the collapse phenomenon is decreased as
is increased. Also the quantum revival is increased but the collapse phenomenon is decreased as 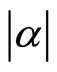 increase (see Figures 1(g)-(i)). These results agree with the case of coherent field but the difference between the coherent state and the nonlinear coherent state appear on the collapse and revival phenomena. For fixed values of the detuning
increase (see Figures 1(g)-(i)). These results agree with the case of coherent field but the difference between the coherent state and the nonlinear coherent state appear on the collapse and revival phenomena. For fixed values of the detuning 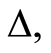 the detuning parameter and the case of absence the nonlinear medium parameter
the detuning parameter and the case of absence the nonlinear medium parameter 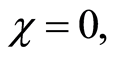 the entropy squeezing factor
the entropy squeezing factor 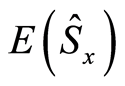 and
and 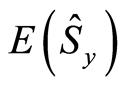 are plotted as a function of the scaled time
are plotted as a function of the scaled time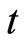 where we set three different values of
where we set three different values of 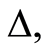 i.e.
i.e.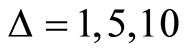 . We noticed no entropy squeezing on the atomic variable
. We noticed no entropy squeezing on the atomic variable  as the detuning parameter increases; see Figures 2(a), (c). Although there is great entropy squeezing on when
as the detuning parameter increases; see Figures 2(a), (c). Although there is great entropy squeezing on when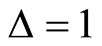 , see Figure 2(d) and no squeezing on
, see Figure 2(d) and no squeezing on 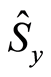 when
when 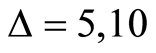 see Figures 2(c) and (f).
see Figures 2(c) and (f).
This is because  then
then
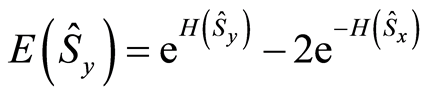 (30)
(30)
where 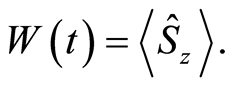 Also one can see as the detuning parameter increased the period of evolution increased. Figure 3 explains the effect of the detuning parameter when the atom is initially in the superposition state of the upper and lower atomic states and all the other parameters are the same as Figure 2. It is observed that the situation is completely different between the excited and superposition states (see Figures 2 and 3) First we see that when the detuning increases, the entropy squeezing on the atomic variables
Also one can see as the detuning parameter increased the period of evolution increased. Figure 3 explains the effect of the detuning parameter when the atom is initially in the superposition state of the upper and lower atomic states and all the other parameters are the same as Figure 2. It is observed that the situation is completely different between the excited and superposition states (see Figures 2 and 3) First we see that when the detuning increases, the entropy squeezing on the atomic variables  increases.
increases.
Also there is a great entropy squeezing on the 
In order to see how the entropy squeezing influenced by the nonlinear medium parameter, we set two different values of the Kerr-medium parameter. Figures 4(a), (d) and (g) show the absence of the nonlinear parameter but

Figure 2. The time evolution of the entropy squeezing factors 
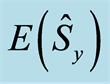 and population inversion
and population inversion 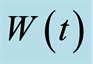 of a two-level atom interacting with a single-mode in the excited state
of a two-level atom interacting with a single-mode in the excited state 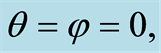 for parameter
for parameter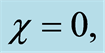
 and with different values of the parameter
and with different values of the parameter  where
where 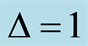 in Figures 2(a) (d) (g),
in Figures 2(a) (d) (g), 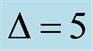 in Figures 2(b) (e) (h) and
in Figures 2(b) (e) (h) and 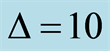 in Figures 2(c) (f) (i).
in Figures 2(c) (f) (i).
Figure 3. The time evolution of the entropy squeezing factors 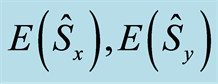 and population inversion
and population inversion  of a two-level atom interacting with a single-mode as Figure 2 but
of a two-level atom interacting with a single-mode as Figure 2 but  and
and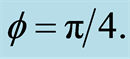

Figure 4. The time evolution of the entropy squeezing factors 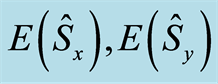 and population inversion
and population inversion 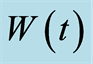 of a two-level atom interacting with a single-mode in the excited state
of a two-level atom interacting with a single-mode in the excited state 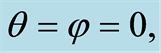 for parameter
for parameter 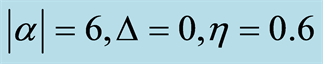 and with different values of the Kerr nonlinearity parameter
and with different values of the Kerr nonlinearity parameter 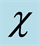 where
where 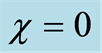 in Figures 4(a) (d) (g),
in Figures 4(a) (d) (g), 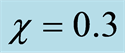 in Figures 4(b) (e) (h) and
in Figures 4(b) (e) (h) and 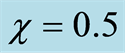 in Figures 4(c) (f) (i).
in Figures 4(c) (f) (i).
the other figures show the influence of the nonlinear parameter. It is remarkable that the nonlinear parameter leads to the following effects, no entropy squeezing occurs on 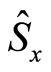 when
when 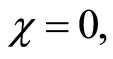 but there is entropy squeezing on
but there is entropy squeezing on  When
When 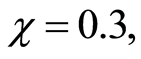 there is an optimal entropy squeezing on both the atomic variables
there is an optimal entropy squeezing on both the atomic variables 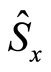 and
and  For large values of
For large values of 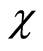 as
as 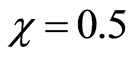 one can see there are more and more optimal entropy squeezing on both of the atomic variables
one can see there are more and more optimal entropy squeezing on both of the atomic variables 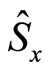 and
and 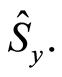
Also the entropy squeezing factors 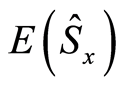 and
and 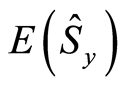 are periodic functions, which have a period
are periodic functions, which have a period 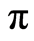 and
and  respectively (see Figures 4(c) and (f)).
respectively (see Figures 4(c) and (f)).
In order to explain the difference between the sources of the radiation fields of the coherent state and the nonlinear coherent state, we must set different values of the Lamb-Diche parameter 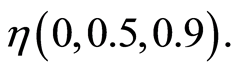 When
When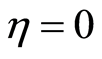 , then the field is initially in the coherent state, but when
, then the field is initially in the coherent state, but when 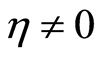 the field is initially in the nonlinear coherent state. Figures 5(a), (d) and (g) show the entropy squeezing in the case of coherent state, which has been examined in many papers [2] [5] [7] . But Figures 5(b), (e) and (h) show the difference between the coherent and new nonlinear coherent states, where we set
the field is initially in the nonlinear coherent state. Figures 5(a), (d) and (g) show the entropy squeezing in the case of coherent state, which has been examined in many papers [2] [5] [7] . But Figures 5(b), (e) and (h) show the difference between the coherent and new nonlinear coherent states, where we set 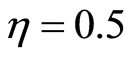 while we set
while we set 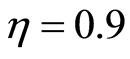 in Figures 5(d), (f) and (i). One can see there is strong entropy squeezing on the atomic variables
in Figures 5(d), (f) and (i). One can see there is strong entropy squeezing on the atomic variables  and there is an entropy squeezing and the period of collapse also increases.
and there is an entropy squeezing and the period of collapse also increases.
6. Conclusions
We have treated the entropy squeezing of a two-level atom when the field is initially prepared in the NCS. New results can be explored as follows.
1) When the field is initially in an NCS, then rich features of the entropy squeezing can be observed, then the entropy squeezing is a good measurement of the information concerning the case of trapped ion.
2) There is a great difference between the influence of the nonlinearity function f(n), which is used in the de-
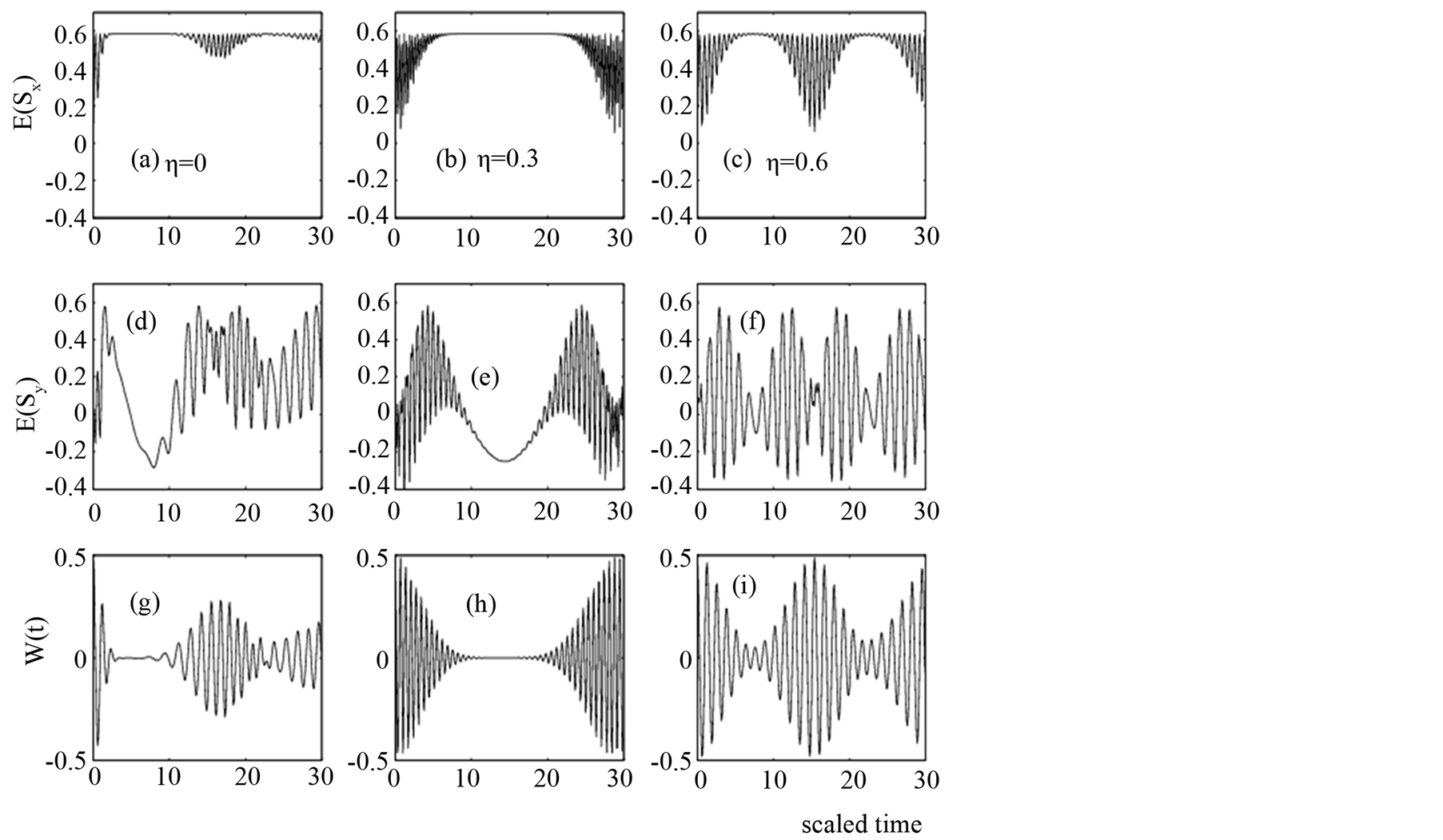
Figure 5. The time evolution of the entropy squeezing factors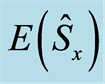 ,
, 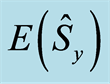 and population inversion
and population inversion  of a two-level atom interacting with a single-mode in the excited state
of a two-level atom interacting with a single-mode in the excited state 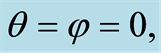 for parameter
for parameter 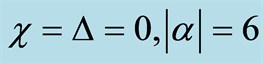 and with different values of the Lamb-Dicke parameter
and with different values of the Lamb-Dicke parameter 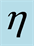 where
where  in Figures (a,d,g),
in Figures (a,d,g), 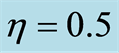 in Figures 5(b) (e) (h) and
in Figures 5(b) (e) (h) and 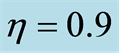 in Figures 5(c) (f) (i).
in Figures 5(c) (f) (i).
scription of the motion of a trapped ion through Lamb-Dicke parameter 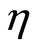 and Kerr medium nonlinearity through parameter
and Kerr medium nonlinearity through parameter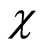 . The first decreases the entropy squeezing but the second increases entropy squeezing.
. The first decreases the entropy squeezing but the second increases entropy squeezing.
References
- Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423.
- Obada, A.-S.F. and Abdel-Aty, M. (2000) Influence of the Stark Shift and Kerr-Like Medium on the Evolution of Field Entropy and Entanglement in Two-Photon Processes. Acta Physica Polonica, B31, 589.
- Steane, A. (1998) Quantum Computing. Reports on Progress in Physics, 61, 117-173. http://dx.doi.org/10.1088/0034-4885/61/2/002
- Roy, B. and Roy, P. (2000) New Nonlinear Coherent States and Some of Their Nonclassical Properties. arXiv: quant-ph/0002043.
- Fang, M.F., Zhou, P. and Swain, S. (2000) Entropy Squeezing for a Two-Level Atom. Journal of Modern Optics, 47, 1043-1053. http://dx.doi.org/10.1080/09500340008233404
- Abdel-Aty, M., Abdel-Khalek, S. and Obada, A.-S.F. (2001) Chaos, Solitons & Fractals, 12, 2015-2022.
- El-Shahat, T.M., Abdel-Khalek, S., Abdel-Aty, M. and Obada, A.-S.F. (2003) Chaos Solitons and Fractals Aspects on Entropy Squeezing of a Two-Level Atom in a Squeezed Vacuum. Journal of Modern Optics, 18, 289-298.
- Kuzmich, A., Molmer, K. and Polzik, E.S. (1997) Spin Squeezing in an Ensemble of Atoms Illuminated with Squeezed Light. Physical Review Letters, 79, 4782-4785. http://dx.doi.org/10.1103/PhysRevLett.79.4782
- Saito, H. and Ueda, M. (1999) Squeezed Few-Photon States of the Field Generated from Squeezed Atoms. Physical Review A, 59, 3959-3974. http://dx.doi.org/10.1103/PhysRevA.59.3959
- Hirschman, L.L. (1957) A Note on Entropy. Journal of Mathematical Physics, 79, 152-156.
- El-shahat, T.M., Abdel-Khalek, S., Abdel-Aty, M. and Obada, A.-S.F. (2003) Aspects on Entropy Squeezing of a Two-Level Atom in a Squeezed Vacuum. Chaos, Solitons & Fractals, 18, 289-298. http://dx.doi.org/10.1016/S0960-0779(02)00652-5
- Obada, A.-S.F., Abdel-Khalek, S., Ahmed, M.M.A. and Abo-Kahla, D.A.M. (2009) The Master Equation for a TwoLevel Atom in a Laser Field with Squeezing-Like Terms. Optics Communications, 282, 914-921. http://dx.doi.org/10.1016/j.optcom.2008.10.073
- Kares, K. (1983) States, Effects ond Operations. Springer, Berlin. El-Shahat, T.M., Abdel-Khalek, S. and Obada, A.-S.F. (2005) Entropy Squeezing of a Driven Two-Level Atom in a Cavity with Injected Squeezed Vacuum. Chaos, Solitons & Fractals, 26, 1293-1307. http://dx.doi.org/10.1016/j.chaos.2005.03.013
- Matos Filho, R.L. and Vogel, W. (1996) Nonlinear Coherent States. Physical Review A, 54, 4560-4563. http://dx.doi.org/10.1103/PhysRevA.54.4560

