ABSTRACT

A class of pseudo distances is used to derive test statistics using transformed data or spacings for testing goodness-of-fit for parametric models. These statistics can be considered as density based statistics and expressible as simple functions of spacings. It is known that when the null hypothesis is simple, the statistics follow asymptotic normal distributions without unknown parameters. In this paper we emphasize results for the null composite hypothesis: the parameters can be estimated by a generalized spacing method (GSP) first which is equivalent to minimize a pseudo distance from the class which is considered; subsequently the estimated parameters are used to replace the parameters in the pseudo distance used for estimation; goodness-of-fit statistics for the composite hypothesis can be constructed and shown to have again an asymptotic normal distribution without unknown parameters. Since these statistics are related to a discrepancy measure, these tests can be shown to be consistent in general. Furthermore, due to the simplicity of these statistics and they come a no extra cost after fitting the model, they can be considered as alternative statistics to chi-square statistics which require a choice of intervals and statistics based on empirical distribution (EDF) using the original data with a complicated null distribution which might depend on the parametric family being considered and also might depend on the vector of true parameters but EDF tests might be more powerful against some specific models which are specified by the alternative hypothesis.

Keywords:

Density Based Tests, EDF Tests, Anderson-Darling Statistic, Hellinger Distance Statistic, Pseudo-Distance, Maximum Spacing Method

1. Introduction

Let $X_1,\cdots ,X_{n-1}$ be a sample of size $n-1$ from a continuous distribution $F\in \left\{F_{\theta }\right\}$ and let $X_1\le \cdots \le X_{n-1}$ be the order statistics and let the transformed data be defined as $U_i\left(\theta \right)=F_{\theta }\left(X_i\right),i=1,\cdots ,n-1$ , $U_{\left(i\right)}\left(\theta \right)=F_{\theta }\left(X_{\left(i\right)}\right),i=1,\cdots ,n-1$ and define $F_{\theta }\left(X_{\left(n\right)}\right)=1$ and $F_{\theta }\left(X_{\left(0\right)}\right)=0$ . The spacings are given by $D_i\left(\theta \right)=F_{\theta }\left(X_{\left(i\right)}\right)-F_{\theta }\left(X_{\left(i-1\right)}\right)$ , $i=1,\cdots ,n$

Ghosh and Jammalammadaka [1] , Luong [2] have studied generalized spacing methods (GSP) of estimation with the vector of GSP estimators given by the vector $\widehat{\theta }$ which minimizes

${\displaystyle {\sum }_{i=1}^{n}h\left(n{D}_i\right)}$ with $h\left(x\right)=-x^{\alpha }$ (1)

Using this class of $h\left(x\right)$ , it is shown that the asymptotic covariance matrix of $\widehat{\theta }$ is given by

$\frac{1}{n}{\sigma }_h^2\left(\alpha \right){\left[I\left(\theta \right)\right]}^{-1}$ with ${\sigma }_h^2\left(\alpha \right)\ge 0$

and ${\sigma }_h^2\left(\alpha \right)$ depends on $\alpha$ but does not depend on the parametric family $\left\{F_{\theta }\right\}$ and $I\left(\theta \right)$ is the usual information matrix of maximum likelihood (ML) estimation.

Furthermore, by letting $\alpha \to 0_{+}$ , ${\sigma }_h^2\left(\alpha \right)\to 1$ . This result is interesting, as it means if we set $\alpha =0.01$ we then have ${\sigma }_h^2\left(\alpha \right)\approx 1.02$ and therefore, the loss of efficiency comparing to ML estimation or maximum spacing (MSP) method is around two percent no matter which parametric model is used. Luong [2] has also shown that this loss of efficiency is compensated by a gain in robustness and it might be preferred to use GSP estimation if ML and MSP estimation are not robust; see Remark 2 as given by Luong [2] (p 632). Furthermore, when there are tied observations, this implies some spacings will be equal to 0 and log of these spacings is undefined so that we might want to use GSP methods instead of maximum spacing method (MSP) method; see Section 5 for tied-observations. MSP method is also called maximum product of spacings method; see Cheng and Stephens [3] .

In this paper, we focus on using this class of GSP methods for construction of goodness-of-fit tests statistics for testing the simple null hypothesis:

H₀: data come from a distribution $F_0=F_{{\theta }_0}$ ; ${\theta }_0$ is specified and for testing the composite null hypothesis.

H₀: data come from the parametric family $F\in \left\{F_{\theta }\right\}$ ; $\theta$ is unspecified. For the composite H₀, Cheng and Stephens [3] have shown that the Moran’s statistic with parameters estimated by the MSP method has an asymptotic normal distribution which does not depend on the parametric family $\left\{F_{\theta }\right\}$ and we shall show that similar properties hold for the class of test statistics constructed using the class of GSP methods being considered in this paper. In a previous paper, we have considered estimation using this class of GSP methods and parameter hypothesis testing. In this paper, we focus on model validation using this class of GSP methods since testing for goodness-of-fit for composite H₀ using GDP methods has not received much attention in the literature.

We adopt an approach using pseudo distances by showing the class of $h\left(x\right)=-x^{\alpha },0<\alpha <1$ induces a class of pseudo distances which we shall denote by $d_{ф}\left(f_1,f_2\right)$ , the function $ф=1-x^{\alpha }=1+h\left(x\right)$ , $f_1$ and $f_2$ are densities and $d_{ф}\left(f_1,f_2\right)$ is a measure to quantify how close these densities are. Implicitly, for methods using spacings we work with transform data and if ${\theta }_0$ is the true parameter then the transform data

$U_i=F_0\left(X_i\right)=F_{{\theta }_0}\left(X_i\right),i=1,\cdots ,n-1$

will follow a standard uniform distribution with density $f_U=1,0\le x\le 1$ and $f_U=0$ , elsewhere.

Using the transformed data we can obtain an easily constructed elementary density estimate without requiring a kernel of the usual density estimate, this empirical density estimate is denoted by ${\widehat{f}}_n$ , see expression (6) and for testing the simple null hypothesis, a test statistic can be constructed which is based on

$n^k{d}_{ф}\left(f_n,f_U\right)$ (2)

with the restriction on $k>0$ and $n^k{d}_{ф}\left(f_n,f_U\right)$ can be reexpressed equivalently as a simple function of spacings and numerically simple to compute; the statistic will follow an asymptotic normal distribution which does not depend on the parametric family. For the statistic to have good power for large samples, it appears that we should choose the scaling factor $n^k$ so that an asymptotic distribution exists for the statistic given by expression (2) and at the same time $k>0$ so that $n^k\to \infty$ as $n\to \infty$ and if $d_{ф}\left(f_n,f_U\right)$ can be used to discriminate whether the sample is drawn from an assumed distribution, the test will be consistent and it is an advantage over chi-square tests which do not have the consistency property, in general.

For the composite hypothesis, we use a GSP method to obtain the GSP estimators given by the vector $\widehat{\theta }$ first but we shall see that minimizing expression (1) is equivalent to minimizing the following pseudo distance based on a function $ф$ , the expression up to a positive multiplicative constant is given by $n^k{d}_{ф}\left(f_n^{\theta },f_U\right)$ , $f_n^{\theta }$ is defined by expression (11) in Section (4).

Subsequently the statistic is based on

$n^k{d}_{ф}\left(f_n^{\widehat{\theta }},f_U\right)$ (3)

and after simplifications, it is reduced to a simple function of spacings with estimated parameters and it will be shown again the equivalent statistic to the one given by expression (3) will follow an asymptotic normal distribution without unknown parameters; this property will facilitate goodness-of-fit testing. Using this unified presentation, we would like to show that these statistics are density based and they are parallel to traditional test statistics based on distribution functions (EDF) such as the Anderson-Darling statistic, see Anderson Darling [4] , Boos [5] , Stephens [6] or chi-square goodness-of-fit statistics with parameters estimated with minimum chi-square methods as discussed by Greenwood and Nikulin [7] (p 70-159).

The approach used in this paper hopefully will unify estimation and model testing and facilitate the comparisons of these density based statistics with traditional EDF statistics and chi-square statistics which are more often used than these density based statistics. We note that these statistics can be computed easily and their null asymptotic distribution is normal without unknown parameters which make it easy to use these statistics and comparing to the related chi-square statistics, these statistics do not need a choice of intervals and they come as by products when fitting models using the corresponding GSP methods. This feature is not shared by maximum likelihood (ML) methods.

We also note that power analysis using theoretical works might not give a complete picture for these density based statistics as the analysis is often based on only one sequence of functions which belongs to the alternative hypothesis converging to the functions specified by the null distribution and there are so many sequences that can approach the functions of the hypothesis in a functional space; see Sethuraman and Rao [8] for Pitman efficiency analysis for these statistics for the simple null hypothesis.

In this paper, we shall concentrate on asymptotic distributions goodness-of-fit tests statistics based on GSP methods and emphasizing a class of GSP methods which complete the results on estimation and parameter testing given by a previous paper. Implicitly, GSP methods in this paper mean GSP methods restricted to the class being considered in this paper. Furthermore, we do not touch upon the question of power analysis which might need extensive simulations studies with many models chosen for the alternative hypothesis as we do not have enough computing facilities and resources for such large scale simulation studies, see Cheng and Stephens [3] (p 386) on power of the Moran’s statistic with the MSP method which is also called maximum product of spacings method; also see Zhang [9] for simulation studies for assessing the power of some EDF tests.

The paper is organized as follows.

In Section 2, a class of pseudo distances which generate the related GSP methods for estimation and model testing is introduced and the inference methods are based on spacings or equivalently on transformed data. The elementary density estimate introduced by Kale [10] is presented in Section 3 and a pseudo distance between the elementary density estimate and the standard uniform density is used to construct goodness-of-fit statistic for testing the simple null hypothesis, the statistic is shown to be expressible as a simple function of spacings which follows an asymptotic normal distribution without unknown parameters under the simple null hypothesis. In Section 4, for testing the composite hypothesis we can choose a GSP method within the class being considered by minimizing a corresponding pseudo distance which implicitly define a GSP method for estimation then use the obtained estimators to replace the unknown parameters in the pseudo distance to construct a goodness-of-fit statistic and after simplification the statistic is expressible as a simple function of spacings with an asymptotic normal distribution which does not depend on the parameters as in the simple null hypothesis case. In Section 5, tied-observations are discussed and it might be more practical to use a GSP method instead of the MSP method as tied observations do not cause numerical difficulties for GSP methods but extra cares are needed if MSP method is used, see Cheng and Stephens [3] (p 391) for tied observation treatments for MSP method. Section 6 gives some discussions on power analysis using theoretical works highlighting that theoretical power analysis might not give a complete picture of power of the statistics due to functions are involved under the null and alternative hypothesis comparing to the classical set up which only involve scalars.

2. Discrepancy Measures or Pseudo Distances

We shall see that pseudo-distances can be created using a convex function $ф\left(x\right),x\ge 0$ with ${ф}^{\prime }\left(x\right)$ and ${ф}^{″}\left(x\right)$ being respectively its first and second derivatives with ${ф}^{″}\left(x\right)\ge 0$ . We focus on pseudo distances defined by using as $ф\left(x\right)=1-x^{\delta },x\ge 0,0<\delta <1$ and let $\alpha =1-\delta$ . The GSP estimators given by the vector $\widehat{\theta }$ can be seen are based on this class as they are obtained by minimizing the following objective function with respect to $\theta$ and by choosing a value for $\alpha$ ,

$T_n\left(\theta \right)=-{\displaystyle {\sum }_{i=1}^n{\left(n{D}_i\left(\theta \right)\right)}^{\alpha }},0<\alpha <1$ ,

i.e., specifying $h\left(x\right)=-x^{\alpha },0<\alpha <1,x>0$ .

We shall see that using this class of $h\left(x\right)$ using spacings is equivalent to use a class of pseudo distances for densities defined using $ф\left(x\right)$ . It has been shown in our previous paper that GSP methods can attain high efficiency for estimation using values for $\alpha$ being positive and near 0.

Note that by letting $\alpha \to 0_{+}$ we obtain full efficiency and with $\alpha =0.05$ , the asymptotic relative efficiency is around 0.98 for all parametric families comparing to fully efficient methods such as the MSP method or ML method or Hellinger method based on density estimate using the original data introduced by Beran [11] . The elementary density estimate which makes use of spacings is based on transformed data and it is easily obtainable without requiring a kernel. The elementary density estimate is due to Kale [10] . We shall introduce it subsequently after the definition of pseudo distance and give an interpretation to GSP methods as minimum distance methods based on pseudo distances which are density based measures of discrepancy. Presenting from this point of view, it parallels the Hellinger methods introduced by Beran [11] with the use of Hellinger distance and the original data. It might be more complicated for practitioners to implement Beran’s minimum Hellinger distance methods which require a kernel density estimate with a choice of window than implementing these GSP methods.

This will also make the GSP methods parallel to EDF methods such as the Cramér Von Mises methods or weighted Cramér-Von Mises distances such as the Anderson-Darling distance methods which also make use of the original data. For Anderson-Darling (AD) distance, see Anderson and Darling [12] . The Anderson-Darling distance is also a pseudo distance which is always nonnegative and measures the discrepancy between two distribution functions and it needs not obey the triangle inequality. Minimizing the discrepancy between the usual empirical distribution and the distribution of the parametric family will give the minimum Anderson-Darling estimators (MAD), see Boos [5] .

In general, the MAD estimators are robust and have high efficiencies but for some parametric families, the overall relative efficiency when compared to maximum likelihood (ML) estimators can fall below 0.80, see Boos [5] (p 2754). Once the MAD estimators given by the vector $\overline{\theta }$ is obtained, the Anderson-Darling distance can be used to form the AD statistic which is given by

$AD\left(\overline{\theta }\right)=n{\displaystyle {\int }_{-\infty }^{\infty }{\left(F_n-F_{\overline{\theta }}\right)}^2\text{d}{F}_{\overline{\theta }}\left(x\right)}$ (4)

to test the validity of the model specified by the composite $H_0:F\in \left\{F_{\theta }\right\}$ , i.e., the data is drawn from a distribution F which belongs to the family $\left\{F_{\theta }\right\}$ and $F_n$ is the usual empirical distribution function using the original data. The expression (4) can also be reexpressed so that it is more suitable for calculations see Boos [5] (p 2748). It has been shown that the null distribution of statistics which is based on empirical distribution function (EDF) such as the AD statistic defined by expression (4) does not have a unique null distribution asymptotically as it will depend on $\left\{F_{\theta }\right\}$ and possibly also on ${\theta }_0\in \theta$ , see Boos [5] (p 2759-2766), Pollard [12] (p 61). Even in the case where the null hypothesis is simple, it is still quite complicated and often extensive simulations are needed to calculate the p-value of such tests or extensive tables are needed for the use of these EDF tests. We shall see that it is not the case for the GSP methods based on the $ф$ functions as we have defined earlier. We focus on this class of $ф$ functions as it can give high efficiency for estimation and the pseudo distances used for estimation can also be used to construct goodness-of-fit statistics. Unlike the EDF test statistics, for statistics using these pseudo distances we have an asymptotic normal distribution as null distribution regardless of the value of the vector ${\theta }_0$ and regardless of $\left\{F_{\theta }\right\}$ for goodness-of-fit the parametric model. The goodness-of-fit statistics are easily obtainable as they are based on the same pseudo distances used for estimation and the statistics can be expressed in an equivalent form as simple functions of the spacings. In this paper, we relate estimation and goodness of fit by considering them as inference methods based on pseudo distances; the approach might provide more insights on the methods using spacings which have appeared in the literature as methods for estimation and testing using spacings are usually presented separately.

Before introducing these goodness-of-fit statistics, first we shall define a ф-discrepancy measure which induces a ф-pseudo-distance. The definitions have been given by Ali and Silvey [13] , Pardo [14] (p 5-7) and reproduced below.

Definition (ф -pseudo-distance)

The ф-pseudo-distance or ф-divergence measure between two densities $f_1$

and $f_2$ is defined by $d_{ф}\left(f_1,f_2\right)=E_{f_2}\left(ф\left(\frac{f_1}{f_2}\right)\right)$ , $E_{f_2}(.)$ is the expectation using

$f_2$ , $ф$ is a convex function with $ф\left(x\right)$ defined for $x\ge 0$ and the second derivative ${ф}^{″}\left(x\right)$ exists and ${ф}^{″}\left(x\right)\ge 0,ф\left(1\right)=0$ .

We have $d_{ф}\left(f_1,f_2\right)\ge 0$ , $d_{ф}\left(f_1,f_2\right)=0$ if and only if $f_1=f_2$ except on a set of measure 0. The discrepancy measure needs not be symmetric as $d_{ф}\left(f_1,f_2\right)\ne d_{ф}\left(f_2,f_1\right)$ and it does not need to obey the triangle inequality and unless otherwise stated, we focus on the class of $ф\left(x\right)=1-x^{\delta },x\ge 0,0<\delta <1$ and let $\alpha =1-\delta$ .

Using the above function, the pseudo distance can be expressed as

$d_{ф}\left(f_1,f_2\right)=1-{\displaystyle {\int }_{-\infty }^{\infty }{\left(\frac{f_1\left(x\right)}{f_2\left(x\right)}\right)}^{\delta }{f}_2\left(x\right)\text{d}x}=1-{\displaystyle {\int }_{-\infty }^{\infty }{f}_1^{\delta }\left(x\right)f_2^{1-\delta }\left(x\right)\text{d}x}$

and we shall use these pseudo distances to construct goodness-of-fit test statistics using transformed data or equivalently spacings and related them with results which already obtained using spacings which have appeared in the literature. The advantage of this approach is an unified treatment can be given to estimation and model testing and it can reveal tests based on statistics which make use of spacings which might not be powerful for large samples when used for testing of goodness-of-fit.

Note that Hellinger distance (HD) which is a true distance as used by Beran [11] can be expressed in a similar form with

$d_{\text{HD}}\left(f_1,f_2\right)={\displaystyle {\int }_{-\infty }^{\infty }{\left(f_1\left(x\right)-f_2\left(x\right)\right)}^2\text{d}x}=2-2{\displaystyle {\int }_{-\infty }^{\infty }{f}_1^{\frac{1}{2}}\left(x\right)f_2^{\frac{1}{2}}\left(x\right)\text{d}x}$ .

In the next section, we shall present an elementary density estimate using transformed data and we aim to test the following simple H₀ which specifies that the random sample of observation is drawn from a distribution function $F_0\left(x\right)=F_{{\theta }_0}\left(x\right)$ , ${\theta }_0$ is specified and $F_0\left(x\right)$ has a closed form expression.

We assume to have a random sample of size $n-1$ which consists of $X_1,\cdots ,X_{n-1}$ and these observations are independent and identically distributed(iid) as X which follows a distribution $F\in \left\{F_{\theta }\right\}$ , $\left\{F_{\theta }\right\}$ is the parametric model used and let the order statistics be denoted by $X_1\le X_2<\cdots \le X_{n-1}$ .The vector of parameters is denoted by $\theta ={\left({\theta }_1,\cdots ,{\theta }_m\right)}^{\prime }$ , ${\theta }_0$ is the true vector of parameters.

If we want to test the simple null hypothesis which specifies that data come from $F=F_0\left(x\right)=F_{{\theta }_0}$ , let $U_i=F_0\left(X_i\right)$ be the transformed data and the order statistics based on transformed data are $U_{\left(1\right)}\le U_{\left(2\right)}\le \cdots \le U_{\left(n-1\right)}$ and the spacings be defined as $D_i=U_{\left(i\right)}-U_{\left(i-1\right)},i=1,\cdots ,n$ with 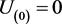and and it is clear that the transformed data will follow a uniform distribution under the null hypothesis. Now using the transformed data and instead of constructing the usual empirical distribution function which is a step function, we use the line segments to join the points where there are jumps so that it becomes a piecewise linear function, i.e., define the following smoothed empirical distribution as given by Kale [10] (p 44),

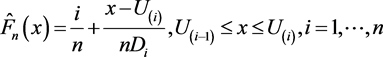(5)

The density function of is

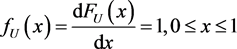and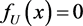, elsewhere. (6)

The procedure to smooth the empirical distribution using transformed data is similar to the procedure of constructing an ogive function when data have been grouped into intervals and we need to smooth the empirical distribution function, see Klugman et al. [15] (p 212) for the ogive function.

The smoothed empirical distribution function admits the following elementary density estimate as density,

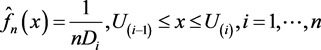(7)

and it can be obtained easily without requiring a kernel and specifying a window.

3. Density Based Statistics for Simple Null Hypothesis

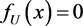It is not difficult to see that under the simple null hypothesis the transformed data follow the uniform distribution with density function given by and elsewhere and an appropriate goodness-of-fit statistic can be based on

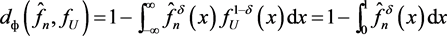
since and elsewhere.

Therefore, if we can find a real number 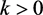so that

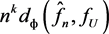(8)

has an asymptotic distribution which no longer depends on the functional form of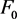, the statistic for testing goodness-of-fit can be based on the statistic 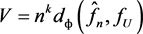and the test will have power since with, this will imply and with being a measure which can detect whether the sample is drawn from an assumed distribution, the statistic given by expression (8) will be able to detect departure from the null hypothesis in probability as.

In fact, we do not need to require, only needs to be defined up to a positive multiplicative constant and an additive constant. In fact, all we need is to have the following main property with the following situations:

1) If the sample is drawn from a distribution F and is constructed based on the transformation applied on the data and we compute, we shall use the notation for computed under situation 1.

2) If the sample is drawn from a distribution G and is constructed based on the transformation F applied on the data and we compute and

we shall use the notation when it is computed under situation 2.

Then, we should have in probability and in general this property holds using Theorem 1 as given by Kirmani and Alam [16] (p 200). Consequently, by having this property, eventually we can detect departure from the null hypothesis as using a statistic based on.

Furthermore, if we can simplify the expression of V so that we can have an equivalent statistic which serves the same purpose and it is simpler to compute then it is interesting to use its equivalent form. It turns out that this is the case as the statistic can be expressed as a simple function of spacings. However, by relating to the discrepancy measure, the test based on such a statistic can be seen to be consistent. This statistic parallels the one proposed by Beran [11] (p 458) which uses the Hellinger distance with the original data and a kernel density estimate. It is simpler to obtain this statistic than the one given by Beran.

Now we shall examine the component of. We observe that

and it can be re-expressed as

, (9)

see Kirmani and Alam [17] for goodness of fit test using statistic of the form. Our approach here is slightly different as we relate the statistic with the pseudo distance and by doing so we can examine the test statistic from two angles and see whether the test statistic might have good power or not for large samples.

Using results as given in section 2 by Luong [2] , we can conclude that

has an asymptotic Normal distribution as a Central limit

Theorem can be applied to the expression. By letting the mean and variance of with W which follows a standard exponential distribution and using the moment generating function of the log-gamma distribution which states that

for,

we have with being the usual gamma function,

,

so that we have an asymptotic normal distribution for the test statistic P defined below and if we need to emphasize the dependence on, we also use the notation

and it is given by with to denote convergence in distribution or in law.

Therefore, if we look for the scaling factor k using expression (9) we should consider

since (10)

and with, this will imply with and the test will have power for large samples. This magnified scaling factor will make the statistic sensitive to departure from the null hypothesis when the sample sizes become large. This property of consistency of the tests did not seem to have received attention in the literature.

The asymptotic distribution of the statistic

which can also be represented as with which

follows a Normal distribution with mean and variance. We should reject H₀ if and b is chosen so that the approximate probability (aP) given by the asymptotic distribution with for a test of size p. From the following equalities,

and hence, , we reject H₀ if

(11)

with being the p-th percentile of the standard normal distribution. Note that we need to restrict to be positive and near 0 as within this range for, GSP methods are efficient for estimation. The test based on Matusita’s distance

or Hellinger distance with using transformed data with the statistic as

given by expression (11) might make the test having low power for large samples when the null hypothesis is composite; see Kirmani and Alam [16] , Kirmani

[17] for the statistic using but with the GSP method is not

efficient for estimation. Testing for the null hypothesis which is composite will be considered subsequently.

4. Density Based Statistics for Null Composite Hypothesis

For testing the null composite hypothesis which specifies that data come from the parametric family and since is unknown, we proceed to estimate by minimizing a chosen pseudo distance based on a value fixed for and subsequently use the same pseudo distance to construct the statistic. The second step is similar to the construction of the statistic for simple null hypothesis as it consists of replacing the unknown parameters with their estimates and once they are replaced, the statistic will have a similar form as in the simple null hypothesis case.

Parallel to the simple null hypothesis case, we transform the data and let and since in this case the U_i’s depend on, we also use the notation and define as before the spacings but they will depend on and given by

with for all, is the parameter space assumed to be compact.

Since the transformed data depends on, we might want to call them pseudo transformed data which leads to define the following pseudo elementary density estimate as

, (12)

using the notations

.

We estimate first by which minimizes which is equivalent to minimize or maximizes.

The estimators given by the vector are Generalized spacing (GSP) estimators with a GSP method using with which is specified.

The goodness-of-fit test statistic can be based on which depends on this time and can be similarly constructed as for the simple hypothesis case with

.

Argue as in the case of simple null hypothesis it leads to consider the equivalent statistic

(13)

We shall show subsequently that we have the equality in distribution

, (14)

is the true vector of parameters, by showing

, is the vector of true parameters, so that we reject the composite null hypothesis if

. (15)

The statistic is similar to the one used for the simple null hypothesis case. All we need is to replace by in the expression of the statistic used for the simple hypothesis.

Observe that we can expand the expression

(16)

around using a Taylor’s type of expansion technique, a technique which is also used in the proof for asymptotic normality of as given in section (3.2) by Luong [2] and let and be respectively the first derivative vector and second derivative matrix and we have since maximizes or minimizes. Therefore, we have the following equality in probability

(17)

with and being bounded in probability as

is up to a constant equivalent to the matrix which is given

by Luong [2] (p 629-630) and has an asymptotic distribution. Now with, we then have with being an expression which converges to 0 in probability. Therefore,

(18)

which justifies the use of expression (15).

The same type of property has been shown to hold for the asymptotic distribution of the Moran’s statistic with Maximum spacing estimators for testing goodness of fit for parametric models, see Cheng and Stephens [3] (p 390).

The GSP methods with might be recommended as it induces a minimum loss of efficiency across parametric models, say with, the loss of efficiency comparing to the MSP method is around two percents only for all the parametric model and the GSP method has some robustness properties like the minimum Hellinger distance estimator proposed by Beran [11] (see Remark 2 given by Luong [2] ). With, the loss of efficiency is around ten per cents. It is simpler to implement GSP methods for estimation, parameter hypothesis testing and goodness of fit testing than implementing Hellinger distance method as proposed by Beran and practitioners might want to use the GSP methods based on this class for their applied works. The equivalent statistic for testing the composite using Hellinger distance which is also density based as proposed Beran [11] (p 459) might be more difficult to implement for practitioners. The same can be said for the test based on Genalized Method of Moments (GMM) using a continuum moment of conditions as proposed by Carrasco and Florens [18] (p 813). Of course, these conclusions are based on the distribution of the parametric family has a closed form expression so that data can be easily transformed which leads to consider spacings for inferences. These density based tests share with chi-square tests with parameters estimated with the minimum chi-square methods to have an asymptotic distribution which does not depend on and since there is no need to choose intervals to perform these tests; this might be viewed as an advantage over the corresponding chi-square tests for testing simple null hypothesis and for composite null hypothesis.

5. Tied Observations

In this section, we would like to make the following remark by pointing out that in a data set which is not large and there are many tied observations, it might be preferred to use a GSP method instead of the MSP method as the MSP method is based on minimizing or maximizing and for two ordered observations which are tied, this implies a spacing is equal to 0 and log of this spacing is undefined, see table 3 in Cheng and Stephens [3] (p 391) which gives a real life data set where tied measurements are recorded.

Cheng and Stephens [3] (p 391) also proposed methods to handle tied observations for the use of MSP method but tied measurements do not cause numerical difficulties for the GSP method as discussed and there is little loss of efficiency using a GSP method and a GSP method might be more robust than the MSP method, see Remark 2 as given by Luong [2] .

6. Discussions

In this section, we touch upon the question of power analysis for these density based tests. Power analysis for null hypothesis which specifies functions is more complicated than Pitman efficiency analysis when parameters are scalars, see Lehmann [19] (p 158-187) for the classical set up with scalars as parameters instead of functions.

Here, under the null hypothesis a function or functions are specified, this makes the study of power more complicated even for the simplest case when the null hypothesis H₀ is simple which specifies the data comes from F₀ or equivalently the transformed data comes from a standard uniform density with density function for and, elsewhere.

For power study, often a sequence of tests based on a sequence of functions which belongs to the alternative hypothesis is considered. Sethuraman and

Rao [8] , used the following sequence of functions with,

is twice differentiable with bounded second derivative and

.

For theoretical works and Pitman efficiencies, the focus is on best tests based on a chosen sequence of functions but it might not provide a complete answer for applications as an optimum statistic might no longer be optimum if another sequence of functions are chosen. In applications, the distributions belonging to the alternative hypothesis which are useful and commonly used might not have been included in the analysis for theoretical works. This makes the assessment of power difficult using theoretical analysis especially when parameters are functions instead of scalars, see Lehman [19] for the classical set up on Pitman efficiency analysis using scalars and parameters belong to the real line. The functional space is more complicated than the real line.

Cheng and Stephens [3] (p 386) recognized this problem and pointed out that power depends on the alternative hypothesis and to get some ideas on the power of these tests often large scale simulations seem to be needed and many parametric families should be considered as given by the alternative hypothesis which are techniques that Zhang [9] has used to conduct power studies for some EDF tests. We do not have resources for these large scale simulation studies. These tests have not been not used extensively and in the future if they are used more frequently and concomitantly with GSP methods for estimation in applications, we will have better ideas on power of these tests.

7. Conclusion

In a previous paper, we have studied estimation, asymptotic properties, robustness and parameter hypothesis testing using GSP methods. In this paper we have adopted the view that GSP methods are minimum density based distance methods using transformed data or equivalently spacings so that estimation and model testing can be treated in a unified way. Model validation via goodness-of-fit tests and construction of density based tests are treated in this paper. We have shown that these statistics for testing come at no extra cost once a GSP method is used for fitting a parametric model and might be useful for assessment of the model in practice. These tests are simple to perform and practitioners might want to use these tests concomitantly with GSP estimation especially when sample sizes are relatively large. For some real life data sets, GSP methods might be preferred over MSP method for estimation and chosen for their robustness property, efficiency and the flexibility to handle tied observations and finally tests statistics for goodness-of-fit can be constructed at no extra cost. The last feature is not shared by maximum likelihood (ML) method.

Acknowledgements

The helpful and constructive comments of a referee which lead to an improvement of the presentation of the paper and support from the editorial staffs of Open Journal of Statistics to process the paper are all gratefully acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Luong, A. (2018) Asymptotic Results for Goodness-of-Fit Tests Using a Class of Generalized Spacing Methods with Estimated Parameters. Open Journal of Statistics, 8, 731-746. https://doi.org/10.4236/ojs.2018.84048

References