Open Journal of Statistics
Vol.05 No.02(2015), Article ID:55869,14 pages
10.4236/ojs.2015.52018
Cheating or Coincidence? Statistical Method Employing the Principle of Maximum Entropy for Judging Whether a Student Has Committed Plagiarism
M. P. Silverman
Department of Physics, Trinity College, Hartford, CT, USA
Email: mark.silverman@trincoll.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 March 2015; accepted 21 April 2015; published 22 April 2015
ABSTRACT
Elements of correspondence (“coincidences”) between a student’s solutions to an assigned set of quantitative problems and the solutions manual for the course textbook may suggest that the student copied the work from an illicit source. Plagiarism of this kind, which occurs primarily in fields such as the natural sciences, engineering, and mathematics, is often difficult to establish. This paper derives an expression for the probability that alleged coincidences in a student’s paper could be attributable to pure chance. The analysis employs the Principle of Maximum Entropy (PME), which, mathematically, is a variational procedure requiring maximization of the Shannon-Jaynes entropy function augmented by the completeness relation for probabilities and known information in the form of expectation values. The virtue of the PME as a general method of inferential reasoning is that it generates the most objective (i.e. least biased) probability distribution consistent with the given information. Numerical examination of test cases for a range of plausible conditions can yield outcomes that tend to exonerate a student who otherwise might be wrongfully judged guilty of cheating by adjudicators unfamiliar with the surprising properties of random processes.
Keywords:
Plagiarism, Cheating, Coincidence, Information, Entropy

1. Introduction
1.1. Cyber-Plagiarism and Why It Matters
Numerous reports over the past decade by the news media [1] -[3] , from private research institutes [4] , in the academic research literature [5] - [8] , and in the literature for a general readership [9] indicate that academic dishonesty, especially in the form of cyber-plagiarism, has been increasing and is currently at an all-time high. Although institutions of higher education have probably had to deal with student cheating since the rise of universities some 800 years ago, what is noteworthy about the current form and extent of academic dishonesty is the pervasive role played by computers, mobile computer-like devices like smart phones, and the Internet.
In brief, portable devices linked to the Internet make it easy for students to rapidly search, download, and insert into exams, homework exercises, and written papers the exact words or calculations of other people without attribution. In the matter of dishonesty in university-level courses in the natural sciences and engineering, improper attribution of credit is usually not the only concern: the very act of submitting someone else’s solution to a problem is not just plagiarism, but a more serious form of cheating. Whereas plagiarism is a kind of intellectual property theft over which academics may argue in regard to definition and importance [9] , but which probably has little impact on the public at large, the pretense to knowledge by a scientist, engineer, or health specialist can lead to serious societal consequences later. For example, science students who get away with cheating throughout university may in the highly competitive world of professional science or medical research be equally disposed to plagiarize, manipulate, or fabricate data leading to fraudulent claims of discovery that waste public funds, foster bad public policies, and harm public health [10] . Thus, it is especially important that students who eventually enter these critical professions should be educated at the outset to know the importance of intellectual honesty.
Nevertheless, to many students, the vastness of the Internet, coupled with the perceived inability of an instructor to verify the originality of all submitted work, provides a sense of security that plagiarism or cheating will go undetected.
1.2. Detection of Plagiarism as a Statistical Challenge
This paper is concerned with assessment of the occurrence of plagiarism in individual cases of a kind that is more likely to be prevalent in the physical sciences, engineering, and mathematics in which assignments call for numerical answers or mathematical analyses with relatively brief written discussion, in contrast to assignments in the humanities and social sciences that often take the form of long papers.
It is relevant to mention that in my own classes, which include technical courses for physics majors as well as general interest courses for students with little science background, I give both kinds of assignments. In the case where a paper is turned in that contains many lines of text plagiarized from an internet-accessible source, there is little if any need for statistical analysis. A student presented with the URL (universal resource locator) and online content that was copied into his or her paper will ultimately admit to the source, since it would be ludicrous to argue that the hundreds of corresponding words in sequence came about by pure chance. (A specious argument that is made by students is that plagiarism did not occur because the copied text was referenced in some way, although never explicitly shown as a direct quotation.)
More problematical, however, is the case where a student’s solution to an assignment suggests elements of correspondence with some other source such as the instructor’s solutions manual to a textbook. The term “elements of correspondence” is unavoidably ambiguous; it may refer to (1) brief verbal phrases occurring in both the student and textbook solutions; (2) the precise format of certain mathematical expressions such as use of a
radical sign 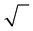 instead of exponent
instead of exponent , or use of vertical fraction
, or use of vertical fraction 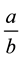 instead of horizontal fraction
instead of horizontal fraction 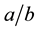
common in multiple places to both student and textbook solutions; (3) the occurrence in the student solution of the same misprints found in the textbook solution; (4) the occurrence of identical diagrams or plots in both the student and textbook solutions, or a variety of other possibilities. This is a matter of perception by the instructor, for which, in view of the intrinsic uncertainty, a statistical analysis and probabilistic inference may be called for.
It has been my experience over many years that few instructors, even among scientists and mathematicians, solve the correct statistical problem when faced with the perception of plagiarism of this kind. The correct problem to be solved is, in fact, a subtle one, with results that can be surprising to the instructor. The problem of assessing whether plagiarism occurs under circumstances where the evidence is suggestive but not conclusive and where the student is adamant about his or her innocence is a vital one because the consequence of a false judgment to a student can be disastrous.
To be clear on the matter of consequence, here is what may transpire at a college or university in the US when a student is accused of plagiarism. An honor panel or committee, comprising an administrator (e.g. a dean of students), faculty, and perhaps also several students, convenes to adjudicate the charge. The accusing instructor presents the case against the student; the student rebuts the accusation; the panel then decides the matter perhaps by simple majority vote.
If the student is found culpable, the penalty can take the form of (1) a permanent or time-limited notice of censure on the student’s academic record; (2) suspension from the institution for a specified period of time; or (3) permanent expulsion from the institution. The lightest penalty (1) is often accorded for first offenses, but its consequences can be far from light. A censured student is no longer in good standing and may be denied academic honors at graduation. If the censure remains on the student’s record at the time the student applies for admission to graduate programs or for financial assistance through graduate fellowships, the applications will likely be unsuccessful since, after all, a graduate school or granting agency would hardly want to foster the education of someone lacking in personal integrity. Moreover, if the censured student is a foreigner, failure to be accepted into a graduate program can result in discontinuation of a student visa, whereupon the student must leave the host country and return home in disgrace. In light of serious potential consequences to a student, the reader can appreciate how critical it is that an honor panel reaches the correct decision.
Different institutions have different protocols, but the foregoing summary is representative. Also characteristic of the procedure is that participants in the honor panels are sought broadly from all faculties of the university and need have no special training or even rudimentary familiarity with probability, statistics, and methods of inferential reasoning. Although administrators, faculty, and students of a university would probably look upon this “diversity” as a laudatory feature of the democratic process, it is also the feature most likely to lead to what in statistical language is termed Type I and Type II errors of judgment [11] . Respectively, these errors amount to rejection of a hypothesis when it is true and acceptance when it is false. However, when the accusing instructor and honor panel are ignorant of the fundamentals of statistics and inferential reasoning, not only is the test of the hypothesis likely to be flawed, but the hypothesis itself that is at issue is likely to be the wrong one. These points are elucidated in the following sections.
2. Case Study of Plagiarism in a Physics Course
2.1. Elements of the Case: Background
The illustrative case to be analyzed is drawn from physics because the fundamental nature of that subject is the most compatible with the kind of plagiarism referred to in Section 1.2. The laws and principles of physics are reproducible statements concerning the physical world accepted without contest (at least provisionally, until demonstrated otherwise by experiment) by the vast majority of physicists. These laws and principles are regarded by physicists as describing the physical world and not the mental state of the physicists who use them; they are expressed through the language of mathematics, and their applications are preferentially mathematical rather than verbal.
In applying these mathematical statements to solve a problem, a physicist or physics student may need to demonstrate that certain conditions prevail under which a particular law is applicable1, but in no case do the actual laws of physics depend on matters like politics, economics, religion, philosophy, or any other aspect of human culture involving potentially divisive interpretations and personal opinions. In other words, physics is a subject for which the corpus of knowledge is reasonably well defined, broadly accepted by practitioners, and very largely independent of cultural biases and opinions.
The point to the preceding two paragraphs is this: In contrast to questions posed in disciplines that call for lengthy discussion, there are usually only a few appropriate ways to solve a well-defined academic physics problem and only one correct answer. There exists, therefore, a possibility for a significant degree of overlap between the sparse verbal and mathematical expressions in the solutions manual and in the exam or homework paper of a physics student, especially if the student is bright and answers questions correctly and in the most efficient way. The difficult issue to be addressed by statistics is whether or not such coincidences signify plagiarism.
2.2. Elements of the Case: The Instructor’s Reasoning
Consider the following representative case, which is an amalgam of situations I have observed:
A student S turns in a homework paper with solutions to 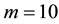 assigned physics problems. The professor P observes elements of correspondence between the instructor’s manual and
assigned physics problems. The professor P observes elements of correspondence between the instructor’s manual and 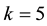 of the student’s solutions. For purposes of simplicity, in view of the previous discussion concerning the brief, mathematical nature of a solution to a physics problem, no distinctions regarding probability of occurrence will be made among the various kinds of elements of correspondence. Nor will the number of such perceived elements in a particular homework problem matter. In this analysis, the only relevant quantification of alleged plagiarism will be the number k of solutions by S out of a total of m problems that P perceives to indicate cheating. I will refer to each such suspicious correlation between a problem worked by S and a problem solved (or looked up in a book) by P as a “coincidence”. As defined in this article, therefore, there can be a maximum of m coincidences, irrespective of the exact number of points of similarity, which is intrinsically subjective, perceived by P.
of the student’s solutions. For purposes of simplicity, in view of the previous discussion concerning the brief, mathematical nature of a solution to a physics problem, no distinctions regarding probability of occurrence will be made among the various kinds of elements of correspondence. Nor will the number of such perceived elements in a particular homework problem matter. In this analysis, the only relevant quantification of alleged plagiarism will be the number k of solutions by S out of a total of m problems that P perceives to indicate cheating. I will refer to each such suspicious correlation between a problem worked by S and a problem solved (or looked up in a book) by P as a “coincidence”. As defined in this article, therefore, there can be a maximum of m coincidences, irrespective of the exact number of points of similarity, which is intrinsically subjective, perceived by P.
P then reasons (either subconsciously to himself or explicitly before the honor panel) in a manner like the following:
“I could accept the possibility that S’s paper contained one problem with wording and equations similar to the solutions manual. But five are too many to be attributable to pure chance. Suppose the probability of a coincidence between a student’s solution and the textbook solution of the same problem is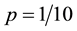 . Then, since the m problems are independent, the probability of five such occurrences would be
. Then, since the m problems are independent, the probability of five such occurrences would be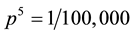 . This probability―one part in one hundred thousand―is so small that it is highly unlikely for the coincidences to have occurred by pure chance. Therefore, S must be guilty of plagiarism.”
. This probability―one part in one hundred thousand―is so small that it is highly unlikely for the coincidences to have occurred by pure chance. Therefore, S must be guilty of plagiarism.”
To members of an honor panel unfamiliar with probability and statistics, the preceding mode of thought may seem rational and convincing. But it is wrong on several accounts.
The first error, known widely in forensic statistics as the “prosecutor’s fallacy” [12] , is the mistaken belief that the probability of occurrence of a rare event is equivalent to the probability that the defendant is innocent. In the present case, P has erroneously conflated the probability that S did not plagiarize with the very small chance of an outcome of 5 coincidences in 10 trials. Expressed generally, the error is to equate the conditional probability 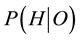 of a hypothesis H given outcomes O with the conditional probability
of a hypothesis H given outcomes O with the conditional probability 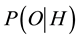 of the outcomes given the hypothesis. The correct relation is given by Bayes’ Theorem [13]
of the outcomes given the hypothesis. The correct relation is given by Bayes’ Theorem [13]
 (1)
(1)
where H is the hypothesis (referred to as the null hypothesis) that the student is guilty of plagiarism, and outcome O is the alleged k coincidences out of m problems. Equation (1) can be re-expressed in the form
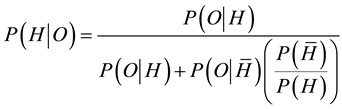 (2)
(2)
in which a bar over a symbol signifies negation. Thus 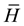 is the hypothesis that the student is not guilty of plagiarism. From Equation (2), it is clear that the conditional probability of guilt given evidence is not equal to the conditional probability of evidence given guilt, but depends as well on the conditional probability of the evidence given innocence and on the prior probabilities of guilt and innocence.
is the hypothesis that the student is not guilty of plagiarism. From Equation (2), it is clear that the conditional probability of guilt given evidence is not equal to the conditional probability of evidence given guilt, but depends as well on the conditional probability of the evidence given innocence and on the prior probabilities of guilt and innocence.
The prosecutor’s fallacy and an analogous specious argument known as the defense attorney’s fallacy have drawn attention of news media, especially in the UK and US, because of its association with sensationalist legal cases such as the Sally Clark cot death case [14] and the O. J. Simpson murder trial [15] . The prosecutor’s fallacy, which can be thought of as an error of quantitative reasoning, is related to, but distinct from, a juridical error concerning which probability actually should be the focus of the honor panel’s deliberations. This point is discussed in the following section, which explains why a different null hypothesis must be adopted.
2.3. The Correct Null Hypothesis
Irrespective of whether P’s calculation was done correctly or not, P was pondering the answer to the wrong question. Implicit to this representative case study is that S had not admitted to any guilt, nor had any evidence been presented to prove guilt, apart from inferences drawn by P from a single homework assignment. Thus, in a society in which the legal system puts responsibility on the part of the accuser to show cause, rather than upon the accused to prove innocence, it ought to be presumed at the outset that S did not commit plagiarism. Under that presumption, the pertinent null hypothesis, therefore, is that the coincidences observed by P occurred by chance. The correct statistical question, therefore, is not what is the probability of plagiarism given coincidences, but this:
What is the probability  that the homework paper turned in by S in a class comprising n students can by pure chance lead to k or more coincidences out of a total of m problems, in which p is the probability of a single such coincidence?
that the homework paper turned in by S in a class comprising n students can by pure chance lead to k or more coincidences out of a total of m problems, in which p is the probability of a single such coincidence?
In other words, in scrutinizing the alleged evidence for plagiarism, the accusing instructor and adjudicating honor panel must focus not on guilt, but on the likelihood that the observed coincidences could have occurred randomly. In the context of a criminal trial, members of a jury are ordinarily unequipped by experience and bias to think this way [16] ―and there is little reason to believe that the diverse members of a university honor panel will collectively think any differently than a trial jury whose members are selected at random from voter registration lists and other lists of non-experts. This presumption is not intended to denigrate the intelligence or intentions of members of university panels. Rather, proper statistical thinking requires proper training without which faculty panels are no less likely to make errors of judgment than have juries in courts of law when presented with misleading statistical arguments.
Bayes’ theorem (2), in which the null hypothesis H is now (and for the remainder of this paper) taken to be that S did not plagiarize, can in principle be used to estimate the probability of S’s innocence given the evidence submitted by P. However, this is not a satisfactory way to proceed because it entails making highly subjective decisions regarding the prior probabilities 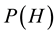 and
and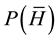 . For example, if S had no prior history of plagiarism and one then set
. For example, if S had no prior history of plagiarism and one then set 

Alternatively, one might argue that the state of ignorance about S’s guilt or innocence is best represented by setting

The primary purpose and accomplishment of this paper is to arrive at an objective probability function with which to infer whether a student may have committed plagiarism or not. As explained in the following sections, this is achieved through use of the principle of maximum entropy (PME), which furnishes a probability distribution, based only on known information, that the observed elements of correspondence between a student’s paper and the instructor’s answer book could have occurred by chance. Subjectivity enters the process only at the endpoint where the honor panel must decide how to use this probability.
2.4. The Correct Solution―Part I: Scoring Coincidences
The problem raised in the case study of this paper calls for a statistical evaluation of the significance of coincidences. The term “coincidence” as defined here is consistent with, although more narrowly focused than, the use of the term by Diaconis and Mosteller [17] in their summary and extension of methods for analyzing coincidences pioneered by eminent biologist and statistician R.A. Fisher [18] . The Fisherian methods highlighted in [18] , which dealt primarily with tests of extrasensory perception and an elaboration of the standard probability model known as the birthday problem [19] , are not particularly suitable to the present case study concerning plagiarism among university science students.
What is noteworthy, however, is Fisher’s use as early as 1924 of 

Also interesting from a historical perspective is that the method of analysis employed here to assess the probability of coincidences likewise draws its inspiration from a distribution initially introduced by Fisher [20] , but for reasons entirely different from those in [18] ―namely, to test for statistical significance in harmonic analysis. Modern developments of this procedure have seen application in testing the power spectrum of radioactive nuclear decay for randomness [21] and in tests of coincidences [22] such as flawed readings of power company electric meters that more closely relate to the statistical model known as a lottery problem [22] [23] than to the birthday problem.
In the analysis of this section, the probability p is taken to be specified a priori. For example, in the (specious) argument of Section 2.2, the professor P instinctively adopted


It then follows that the probability that the student’s paper does not contain at least k coincidences is

Equation (4) therefore gives the probability that the student’s paper contains a number of coincidences ranging from 0 to
Since it is assumed that the students in the class act independently (an assumption that does not hold when students are permitted to collaborate on homework, which is ordinarily not the case in university science courses), the probability that no student in the class of n students has turned in a paper with at least k coincidences is given by

Therefore, the probability

Equation (6) is the sought-for probability function by which to test the significance of alleged coincidences signifying plagiarism under the circumstances outlined in previous sections.
A graphical examination of the statistical content of Equation (6) will be undertaken in a following section, but first it is necessary to consider how to assign a reasonable value to the probability p. There are several ways this might be done of which the final method based on the PME is the most objective:
Method I: p is simply specified by the course instructor based on his/her personal feelings as to what is reasonable. In the hypothetical illustration of Section 2.2 (which reflects an actual occurrence), the accusing professor was comfortable with
Method II: Calculate a value 




A difficulty with Method II is that, like Method I, it is also highly subjective. The value of p is obtained from an arbitrary statistical threshold, which could have been set differently. Therefore




Method III: Use the principle of maximum entropy (PME) to determine the distribution of p. The PME yields the least biased probability distribution consistent with known information. Moreover, since the procedure yields a distribution function and not merely an arbitrary value of p, one can determine the uncertainty (e.g. variance) and other statistical moments. An explanation of the method is given in the following section.
2.5. The Principle of Maximum Entropy (PME)
The term “entropy” in physics (derived from the Greek root for “change”), together with “energy” (derived from the Greek root for “work”), is a seminal concept in thermodynamics and statistical mechanics. It is beyond the scope of this article to explain in detail the various meanings and applications of entropy. (See, however, Ref. [22] for more comprehensive treatment.) Suffice it to say, that, whereas energy is a measure of the work provided or required by a physical process, entropy is a measure of the direction that the process can take and its maximum theoretical efficiency.
Besides the association, known since the 19th Century, of entropy with physical processes involving exchange of work and heat, a connection between entropy and the concept of information was recognized by C.E. Shannon in the late 1940’s [24] . The problem studied by Shannon was to determine the maximum information that could be transmitted through a noisy communication channel. Given a message expressible by a finite set of symbols 


Equation (7) bears a resemblance to the quantity (called “Fisher information”) adopted by Fisher to score coincidences. The two expressions for information have very different properties; the more significant quantity by far is Shannon’s H.
It is demonstrable in equilibrium statistical mechanics (ESM) that the thermodynamic entropy (ordinarily symbolized by S) is equal to the Shannon entropy H up to a universal scale factor, i.e. 

Jaynes, however, developed the method beyond ESM to show that it represented a general mathematical principle of inferential reasoning, not tied to physics, by which to derive the least biased probability distribution consistent with known information [27] . In generalizing the PME, Jaynes modified the form of the Shannon entropy by inclusion of a Lebesgue metric

to ensure that the entropy (i.e. information) is invariant under a transformation of parameters. In other words, if the probability density function of a distribution is first characterized by parameters 




relation for probabilities
As a matter of terminology, it is important not to confuse the principle of maximum entropy (PME) with the different, but statistically more familiar, method of maximum likelihood (MML) introduced early in the 20th Century by Fisher [28] as a method of parameter estimation alternative to use of Bayes’ Theorem. To apply the MML one maximizes the likelihood function, which is a conditional probability function, with respect to the unknown parameters to be estimated. To apply the PME, however, one maximizes the entropy with respect to the unknown probabilities subject to specified expectation values of system properties. The MML yields estimators with certain optimal statistical properties relating to asymptotic normality, sufficiency, minimum variance, and other features (see [11] [22] ). The PME, in contrast, yields the functional form of a probability distribution with parameters (Lagrange multipliers) to be determined from the given expectation values.
The PME distribution is least biased because it depends only on the given information and not on any supplementary assumptions either explicit or implicit. For example, in the case of a sought-for probability distribution contingent on the expectation values of several independent system properties, the PME distribution will lead to zero cross-correlation of these properties. Distributions arising from variation of other functionals than the Shannon-Jaynes entropy (8) ordinarily give rise to non-vanishing cross-correlations of system properties. Clearly, if the given information did not include correlations among the system properties, then an unbiased probability distribution must not generate any.
2.6. The Correct Solution―Part II: Maximum Entropy Probability of Coincidence
The PME solution to a statistical problem employs only (1) the mathematical properties of probability and (2) whatever information is specified―i.e. has been observed―about the system at issue. Regarding information (1), it is assumed that the probability 


If no other information than completeness is available, the solution to the PME variational problem leads to 

In dealing with alleged plagiarism by a student, however, the accusing instructor P and adjudicating panel can acquire an important piece of information: the mean number 


Here, then, is the formal problem to be solved:
Statement of the problem: Find the probability 
(1) Completeness Relation:

(2) Observed Mean:

The functional 

is the Jaynes entropy (8) (with Lebesgue metric






As previously stated, the Lebesgue metric for a given system is proportional to the prior distribution in absence of all information other than the completeness relation. In the present case, therefore, one can set

which is a binomial distribution because there are m possible outcomes (i.e. homework solutions) with only two outcome categories (coincidence or no coincidence) for each solution, and the principle of insufficient reason assigns equal probability to each outcome in the absence of information to the contrary.
Solving the set of equations

to obtain probabilities 

where the Lagrange multiplier 
Despite the appearance of the exponential factor, Equation (14) is not the probability function of an exponential distribution 


from which it follows that

Upon substitution of Equation (16) into Equation (10) and transformation of variable

Use of Equation (17) in Equation (16) leads to the final form of the coincidence probability distribution

which upon substitution into Equation (6) provides the least biased probability function

for judging whether the occurrence of k or more coincident solutions out of m homework problems is acceptable or implausible within a class of n students for which 
It is to be noted that the PME solution (18) is actually a binomial distribution 


parameter

The implications of Equation (19) will next be considered.
3. Probability of Occurrence of Coincidences: Some General Features
The simplest way to get a sense of the information content of Equation (19) is to examine a number of test situations graphically. Recall that Equation (19) is the probability that at least one student in a class of n students will turn in a homework paper of m solutions with k or more random coincidences with the instructor’s answer book. The mean number of such chance occurrences for this assignment in a population comprising all the students in the class is


Figure 1 immediately shows that if the mean number of coincidences is 1 out of 10 solutions, then the probability of a student (i.e. any one or more students in the class) turning in a homework assignment with at least 4 coincidences with the answer book exceeds the standard 5% statistical threshold (dashed line in the figure) in a class of 10 or more students. Ten students in a science course is a small number. A special-topics physics course
Figure 1. Plot (solid line) of the plagiarism test probability 



at the 3rd or 4th year level at a US liberal arts college might well have about 10 students. An outcome of 5 coincidences or more exceeds the 5% threshold in a class size of 30 or more students. Thirty students is not unusual for an introductory general physics course at 1st or 2nd year level at a US liberal arts college. The corresponding class size at a US university could be well beyond 30, and easily exceed 100.
If a set of assigned problems is particularly easy, as may be the case if the instructor puts little time into the task and uses the same questions from year to year, then the mean number of coincidences may be higher than 1. From Figure 2 and Figure 3 one sees that the probability of 5 or more coincidences out of 10 problems exceeds the 5% statistical threshold in a class size smaller than 10 for 

Figure 2. Plot description is the same as Figure 1, except that the mean number of coincidences is
Figure 3. Plot description is the same as Figure 1, except that the mean number of coincidences is
An alternative way to examine the implications of Equation (19) is illustrated in Figure 4, which plots the probability 




To return to the hypothetically constructed (but accurately representative) scenario of Section 2.2, an instructor, faced with a student paper containing 5 solutions out of 10 problems allegedly coincident with the answer book, judged the probability of the event to be implausibly low:


The point of examples like these is to illustrate how counterintuitive the chance of occurrence of random coincidences may seem, especially to people who have had little exposure to probability theory and statistical analysis. Indeed, I have found [22] [30] , that the probabilities and patterns of random events can surprise even scientists and engineers trained in the use of statistics.
4. Conclusions
4.1. Key Points of Statistics and Justice
Widespread occurrence of plagiarism and related forms of academic dishonesty facilitated by access to the Internet is an increasingly serious matter at universities and colleges. While it is understandable that the faculty and administrators of institutions of higher learning will want to take strong and decisive action against perpetrators,
Figure 4. Plot (solid line) of the plagiarism test probability 



it is also necessary to be mindful that false judgments can damage or destroy the careers of nonculpable students charged with plagiarism. This balance of judgments is particularly critical in cases such as may occur in the physical sciences, engineering, mathematics, and other quantitative disciplines in which outright plagiarism is harder to recognize than in the humanities and social sciences because of the greater possibility for overlap (i.e. coincidence) between the written work submitted by a student and the instructor’s solutions to the same problems.
The analysis of this paper leads to a probability function by which to determine the statistical significance of such coincidences. It is to be emphasized that use of the term “coincidence” does not mean merely that a student’s numerical answer to a problem coincides with the instructor’s answer. For an advanced course in a quantitatively rigorous subject like physics or engineering, an instructor might generally expect most students in the class to answer problems correctly. Rather, the term “coincidence” refers to unusually close elements of correspondence between the expression of the student’s solutions and instructor’s solutions that might suggest illicit copying.
The methodology of this paper addresses two seminal questions:
(1) WHICH PROBABILITY?
ANSWER: In the interest of fairness to an accused student who has denied culpability, the adjudicating panel should ascertain the probability that the evidence offered by the accuser could be plausibly attributable to pure chance. This emphasis is diametrically opposite to that of many trial juries in the US and UK [16] and university judicial panels which focus instead on the likelihood that a defendant is guilty of the charge.
(2) HOW TO CALCULATE?
ANSWER: The Principle of Maximum Entropy (PME) provides the most objective method of determining the probability distribution of coincidences consistent with known or readily ascertainable statistical information.
Implementation of the PME entails maximization of the Shannon-Jaynes entropy 





Note that a statistical threshold, whether 5% or some other adopted value, serves only for assisting the adjudicating panel to decide how to act upon the objectively calculated PME probability (19)―that is, for judging whether the resulting probability is sufficiently high to sustain the null hypothesis of random coincidences between the solutions of student S and the answers of professor P. Arbitrary thresholds of significance play no role in the calculation of the probability of coincidence.
4.2. Reducing the Value of Plagiarism in Science Courses
The PME calculation of probability provides an unbiased method of inferential reasoning in the absence of complete information. The interpretation of the statistical significance of this probability is the only point at which a subjective judgment enters. Nevertheless, there is always a non-zero chance that inferential reasoning, however, unbiased and carefully executed, may still lead to a false judgment. The results of this paper permit one to calculate what that chance is. To reduce that chance to zero, however, is not a matter of statistics, but requires fundamental changes in the way courses are taught. I offer the following suggestions drawn from my own teaching experiences at all levels of undergraduate and graduate instruction in physics.
Since opportunities for plagiarism will, if anything, only increase as more information, including solutions manuals to standard textbooks, are legitimately or illegitimately posted on the Internet, the most effective course of action is to adopt a teaching strategy whereby plagiarism confers no advantage.
In my own courses, I inform students at the start of each academic period (of duration one semester where I work) that assigned homework problems are exclusively for their own benefit to help them determine to what extent they understand the concepts and examples worked out in class. Consequently, students are not penalized for errors in their homework, nor are they rewarded for solving problems correctly. Students are permitted to work together on problems and to use various resources, including the Internet, for assistance if necessary―although they are urged to try to do assignments by themselves first and not simply to copy someone else’s work.
A due date is given for each problem set, at which time solutions to the problems are posted, and the next set of problems is assigned. The students’ homework papers are not graded, but may be collected to give me an evolving sense of how individual students and the class as a whole are dealing with the subject matter of the course.
Students who turn in papers with solutions copied from the Internet or some other source reap no benefit in the form of points toward their course grade. The advantage, however, to students who have worked the problems for themselves is that they presumably have acquired a deeper understanding of the subject matter than the copiers and will perform better on tests that actually contribute to their grades. Under the conditions of a test, devices of all kinds (computers, mobile phones, etc.) that connect to the Internet are not permitted in class; the only auxiliary device students may use is a hand calculator.
It is possible, of course, that a student who copied solutions from the Internet may nevertheless have understood the material well enough to get a good grade on a test. To an ethical “purist” who believes that no bad act should go unpunished, the thought of allowing a student who plagiarized an assignment, even one that is not graded, to escape judgment may be unacceptable. To this objection I can only reply that there is no practical way to prevent students from searching the Internet if they are determined to do so. An instructor can only take steps, such as outlined above, to ensure that copying from the Internet or any other source brings no reward.
One final point: Besides tests, an important part of a student’s grade in nearly every science course that I teach is a written paper and associated in-class, computer-projected slide presentation of a topic pertinent to the course that each student researches during the academic period. Early in the semester, students are informed about, and warned against, committing plagiarism in their research projects. For assignments of this kind, which entail extensive research, writing, and speaking (in contrast to relatively brief mathematical solutions of quantitative problems), the occurrence of plagiarism is usually readily discernable and easily provable even without formal statistical analysis.
References
- Kelly, T. (2011) College Plagiarism Reaches All Time High: Pew Study. Huffington Post (1 September 2011). http://www.huffingtonpost.com/2011/09/01/college-plagiarism-all-ti_n_944252.html
- Blum, S.D. (2009) Academic Integrity and Student Plagiarism: A Question of Education, Not Ethics. The Chronicle of Higher Education (20 February 2009). http://chronicle.com/article/Academic-IntegrityStud/32323/
- Odom, T.W. (2015) Cheating in Schools in Rampant. But There’s an Easy Fix. Washington Post (13 March 2015). http://www.washingtonpost.com/posteverything/wp/2015/03/13/cheating-in-schools-is-rampant-but-theres-an-easy-fix/
- Parker, K., Lenhart, A. and Moore, K. (2011) The Digital Revolution and Higher Education. Pew Research Center: Internet, Science & Tech (28 August 2011). http://www.pewinternet.org/2011/08/28/the-digital-revolution-and-higher-education/
- Olafson, L., Schraw, G. and Kehrwald, N. (2014) Academic Dishonesty: Behaviors, Sanctions, and Retention of Adjudicated College Students. Journal of College Student Development, 55, 661-674. http://dx.doi.org/10.1353/csd.2014.0066
- Vandehey, M., Diekhoff, G. and LaBeff, E. (2007) College Cheating: A Twenty-Year Follow-Up and the Addition of an Honor Code. Journal of College Student Development, 48, 468-480. http://dx.doi.org/10.1353/csd.2007.0043
- McCabe, D.L. (2005) Cheating among College and University Students: A North American Perspective. International Journal for Educational Integrity, No. 1. http://www.ojs.unisa.edu.au/index.php/IJEI/article/view/14
- Scanlon, P.M. and Neumann, D.R. (2002) Internet Plagiarism among College Students. Journal of College Student Development, 43,374-385.
- Blum, S.D. (2009) My Word!: Plagiarism and College Culture. Cornell University Press, Ithaca.
- Grant, B. (2015) HIV Scientist Pleads Guilty to Fraud. The Scientist (26 February 2015). http://www.the-scientist.com/?articles.view/articleNo/42285/title/HIV-Scientist-Pleads-Guilty-to-Fraud/
- Mood, A.M., Graybill, F.A. and Boes, D.C. (1974) Introduction to the Theory of Statistics. 3rd Edition, McGraw-Hill, New York, 405-406.
- Fenton, N. (2011) Improve Statistics in Court. Nature, 479, 36-37. http://dx.doi.org/10.1038/479036a
- Kendall, M.G. and Stuart, A. (1963) The Advanced Theory of Statistics, Volume 1: Distribution Theory. 2nd Edition, Hafner, New York, 198-201.
- Hill, R. (2005) Reflections on the Cot Death Cases. Significance, 2, 13-16. http://dx.doi.org/10.1111/j.1740-9713.2005.00077.x
- Gigerenzer, G. (2003) Reckoning with Risk: Learning to Live with Uncertainty. Chapter 8, Penguin E-Book.
- Gardner-Medwin, T. (2005) What Probability Should a Jury Address? Significance, 2, 9-12. http://dx.doi.org/10.1111/j.1740-9713.2005.00076.x
- Diaconis, P. and Mosteller, F. (1989) Methods for Studying Coincidences. Journal of the American Statistical Association, 84, 853-861. http://dx.doi.org/10.1080/01621459.1989.10478847
- Fisher, R.A. (1924) A Method of Scoring Coincidences in Tests with Playing Cards. Proceedings of the Society for Psychical Research, 34, 181-185.
- Parzen, E. (1960) Modern Probability Theory and Its Applications. Wiley, Hoboken, 46-47.
- Fisher, R.A. (1929) Tests of Significance in Harmonic Analysis. Proceedings of the Royal Society A, 125, 54-59. http://dx.doi.org/10.1098/rspa.1929.0151
- Silverman, M.P. and Strange, W. (2009) Search for Correlated Fluctuations in the β+ Decay of Na-22. Europhysics Letters, 87, Article ID: 32001. http://dx.doi.org/10.1209/0295-5075/87/32001
- Silverman, M.P. (2014) A Certain Uncertainty: Nature’s Random Ways. Cambridge University Press, Cambridge, 157-160, 565-567.
- Uspensky, J.V. (1937) Introduction to Mathematical Probability. McGraw-Hill, New York, 19-20.
- Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423. http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x
- Greiner, W., Neise, L. and Stocker, H. (1987) Thermodynamics and Statistical Mechanics. Springer, Berlin, 149-152.
- Jaynes, E.T. (1957) Information Theory and Statistical Mechanics. Physical Review, 106, 620-630. http://dx.doi.org/10.1103/PhysRev.106.620 Jaynes, E.T. (1957) Information Theory and Statistical Mechanics, II. Physical Review, 108, 171-190. http://dx.doi.org/10.1103/PhysRev.108.171
- Jaynes, E.T. (1968) Prior Probabilities. IEEE Transactions on Systems Science and Cybernetics, SSC-4, 227-241. Reprinted in Rosenkrantz, R.D. and Jaynes, E.T., Eds. (1989) Papers on Probability, Statistics, and Statistical Physics. Kluwer, 116-130.
- Fisher, R.A. (1925) Theory of Statistical Estimation. Proceedings of the Cambridge Philosophical Society, 22, 700- 725.
- Keynes, J.M. (1962) The Principle of Indifference. A Treatise on Probability. Chapter IV, Harper Torchbook, New York, 41-64.
- Silverman, M.P., Strange, S., Silverman, C.R. and Lipscombe, T.C. (1999) On the Run: Unexpected Outcomes of Random Events. The Physics Teacher, 37, 218-225. http://dx.doi.org/10.1119/1.880232
NOTES
[1] For example, to use the “law of conservation of energy”, one must first show that the interactions of the physical system are invariant under time translation.







