Received 1 October 2014; revised 28 October 2014; accepted 15 November 2014

ABSTRACT

In this paper, we consider the problem of variable selection and model detection in additive models with longitudinal data. Our approach is based on spline approximation for the components aided by two Smoothly Clipped Absolute Deviation (SCAD) penalty terms. It can perform model selection (finding both zero and linear components) and estimation simultaneously. With appropriate selection of the tuning parameters, we show that the proposed procedure is consistent in both variable selection and linear components selection. Besides, being theoretically justified, the proposed method is easy to understand and straightforward to implement. Extensive simulation studies as well as a real dataset are used to illustrate the performances.

Keywords:

Additive Model, Model Detection, Variable Selection, SCAD Penalty

1. Introduction

Longitudinal data arise frequently in biological and economic applications. The challenge in analyzing longitudinal data is that the likelihood function is difficult to specify or formulate for non-normal responses with large cluster size. To allow richer and more flexible model structures, an effective semi-parametric regression tool is the additive model introduced by [1] , which stipulates that

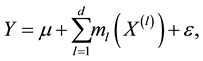(1)

where is a varaible of interest and is a vector of predictor variables, 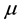is a unknown constant, and are unknown nonparametric functions. As in most work on nonparametric smoothing, estimation of the non-parametric functions 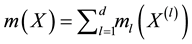is conducted on a compact support. Without loss of generality, let the compact set be and also impose the condition which is required for identifiability of model (1.1),. We propose a penalized

method for variable selection and model detection in model (1.1) and show that the proposed method can correctly select the nonzero components with probability approaching one as the sample size goes to infinity.

Statistical inference of additive models with longitudinal data has also been considered by some authors. By extending the generalized estimating equations approach, [2] studied the estimation of additive model with longitudinal data. [3] focuses on a nonparametric additive time-varying regression model for longitudinal data. [4] considered the generalized additive model when responses from the same cluster are correlated. However, in semiparametric regression modeling, it is generally difficult to determine which covariates should enter as nonparametric components and which should enter as linear components. The commonly adopted strategy in practice is just to consider continuous entering as nonparametric components and discrete covariates entering as parametric. Traditional method uses hypothesis testing to identify the linear and zero component. But this might be cumbersome to perform in practice whether there are more than just a few predictor to test. [5] proposed a penalized procedure via the LASSO penalty; [6] presented a unified variable selection method via the adaptive LASSO. But these methods are for the varying coefficient models. [7] established a model selection and semiparametric estimation method for additive quantile regression models by two-fold penalty. To our know- ledge, the model selection and variable selection simultaneously with longitudinal data have not been investi- gated. We make several novel contributions: 1) We develop a new strategies for model selection and variable selection in additive model with longitudinal data; 2) We develop theoretical properties for our procedure.

In the next section, we will propose the two-fold SCAD penalization procedure based on QIF and compu- tational algorithm; furthermore we present its theoretical properties. In particular, we show that the procedure can select the true model with probability approaching one, and show that newly proposed method estimates the non-zero function components in the model with the same optimal mean square convergence rate as the standard spline estimators. Simulation studies and an application of proposed methods in a real data example are included in Sections 3 and 4, respectively. Technical lemmas and proofs are given in Appendix.

2. Methodology and Asymptotic Properties

2.1. Additive Models with Two Fold Penalized Splines

Consider a longitudinal study with subjects and 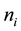observations over time for the ith subject for a total of observation. Each observation consists of a response variable 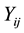and a covariate

vector 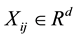taken from the ith subject at time. We assume that the full data set

is observed and can be modelled as

(2)

where is random error with and.

At the start of the analysis, we do not know which component functions in model (1.1) are linear or actually zero. We adopt the centered B-spline basis, where is a basis system and. Equally-spaced knots are used in this

article for simplicity of proof. Other regular knot sequences can also be used, with similar asymptotic results. Suppose that can be approximated well by a spline function, so that

(3)

To simplify notation, we first assume equal cluster size, and let, be the collection of the coefficients in (2.3), and, denote and, then we have an approximation . We can also write the approximation of (2.1) in matrix notation as

(4)

where, and. [8] introduced the QIF that approximates the inverse of by a linear combination of some basis matrixes, i.e.

where is the identity and are known symmetric basis matrices and are unknown constants. The advantage of the QIF approach is that it does not require the estimation of the linear coefficients 's associated with the working correlation matrix, which are treated as nuisance parameters here.

(5)

The vector contains more estimating equations than parameters, but these estimating equations can be combined optimally using the generalised method of the moment. So according to [8] , the QIF approach estimates by setting as close to zero as possible, in the sense of minimizing the quadratic inference function.

(6)

where

Our main goal is to find both zero components (i.e.,) and linear compoents (i.e., is a linear

function). The former can be achieved by shrinking to zero. For the latter, we want to shrink the second derivative to zero instead. This suggests the following minimization problem

(7)

where and are two penalties used to find zero and linear coefficients respectively, with two regularization parameters and, and,. Note that since and

and can be equivalently written as and respectively, with entry of being.

2.2. Asymptotic Properties

To study the rate of convergence for and, we first introduce some notations and present regularity conditions. We assume equal cluster sizes, and are i.i.d. from with, and. For convenience, we assume that is truly nonparametric

for, is linear for, and is zero for. The asymptotic result still hold for data with unequal cluster sizes using a cluster-specific transformation as discuss in [4] . For any matrix, denotes the modulus of the largest singular value of. To prove the theoretical arguments, we need the following assumptions:

(A1) The covariates are compactly supported, and without loss of generality, we assume that each has support. The density of, denoted by, is absolutely conti- nuous and there exist constants and such that for all.

(A2) Let. Then is positive definite and for some,.

(A3) For each, has continuous derivatives for some.

(A4) (8)

(A5) Let. Assume the modular of the singular value of is bounded away from 0 and infinity.

(A6) The matrix defined in Theorem 3 is positive definite.

Theorem 1. Suppose that the regularity conditions A1-A5 hold and the number of knots,. Then there exists a local minimizer of (2.7) such that

For, it reduces to a special case where the responses are i.i.d. The rate of convergence given here is the same optimal rate as that obtain for polynomial spline regression for independent data [9] [10] . The main advantage of the QIF approach is that it incorporates within-cluster correlation by optimally combing estimating equations without estimating the correlation parameters. the estimator of two fold penalized QIF achieve the same rate of convergence as un-penalized estimator. Furthermore, we prove that the penalized estimators in Theorem 1 possess the sparsity property, almost surely for. The sparsity property ensures that the proposed model selection is consistent, that is, it selects the correct variables with probability tending to 1 as the sample size goes to infinity.

Theorem 2. Under the same assumptions of Theorem 1, and if the tuning parameter. Then with probability approaching 1.

a)

b) is a linear function for

Theorem 2 also implies that above additive model selection possesses the consistency property. The results in Theorems 2 are similar to semiparametric estimation of additive quantile regression model in [7] . However, the theoretical proof is very different from the penalized quantile loss function due to the two fold penalty and longitudinal data.

Finally, in the same spirit of that [11] , we come to the question of whether the SIC can identify the true model in our setting.

Theorem 3. Suppose that the regularity conditions A1-A5 hold and the number of knots

as assumed in Theorem 1, The parameters and selected by SIC can select the true model with pro- bability tending to 1.

3. Simulation Study

In this section, we conducted Monte Carlo studies for the following longitudinal data and additive model. the continuous responses are generated from

(9)

where and the number of clusters. The additive functions are

. Thus the last 5 variables in this model are null variables and do not contribute the model. The covariates are generated independently from uniform. The error follows a multivariate normal distribu-

tion with mean 0, a common marginal variance, it has first-order autoregressive (AR-1) and an com- pound symmetry (CS) correlation (i.e. exchangeable correlation) structure with different within correlation coefficient, and consider and representing a strong and weak within correlation structure.

The predictors are generated by, , , where is the standard normal c.d.f. and. The parameter controls the correlation between.

To illustrate the effect on estimation efficiency, we compare the penalized QIF approach in [4] (PQIF) and an Oracle model (ORACLE). here the full model consists of all ten variable, and oracle model only contains the first five relevant variables and we know it’s a partial additive model. The oracle model is only available in simulation studies where the true information is known. In all simulation, the number of replications is 100 and the result are summarized in Table 1 and Table 2. In Table 1, the model selection result for both our procedure

with the one penalty QIF when the error are Gaussian, and we also list the oracle model as a benchmark, the oracle model is only available in simulation studies where the true information is known in Table 1, in which the column labeled “NNC” presents the average number of nonparametric components selected, the column “NNT” depicts the average number of nonparametric components selected that are truly nonparametric (truly nonzero for one penalty QIF), “NLC” presents the average number of linear components, “NLT” depicts the average number of linear components selected that are truly linear.

In Ta ble 2, we conduct some simulations to evaluate finite sample performance of the proposed method. Let be the estimator of a nonparametric function and be the grid points, the performance of

estimator will be assessed by using the square root of average square errors(RASE), we compare the performance of above estimators. On the nonparametric coponents, the errors for estimators with a single penalty and our procedure are similar, and both are qualitatively close to those of the oracle estimator. However, for the parametric components, our estimator is obviously more efficient,leading to about 40% - 50% reduction in RASE.

4. Real Data Analysis

In this subsection, we analyze data from the Multi-Center AIDS Cohort Study. The dataset contains the human immunodeficiency virus, HIV, status of 283 homosexual men who were infected with HIV during the follow-up period between 1984 and 1991. All individuals were scheduled to have their measurements made during semi- annual visits. Here denotes the time length in years between seroconversion and the j-th measurement of the i-th individual after the infection. [12] analyzed the dataset using partial linear models. The primary interest was to describe the trend of the mean CD4 percentage depletion over time and to evaluate the effects of cigarette smoking, pre-HIV infection CD4 percentage, and age at infection on the mean CD4 cell percentage after the infection.

In our analysis, the response variable is the CD4 cell percentage of a subject at distinct time points after HIV infection. We take four covariates for this study:, the CD4 cell percentage level before HIV infection; and, age at HIV infection; the individual’s smoking status, which takes binary values 1 or 0, according to whether a individual is a smoker or nonsmoker; denote, denotes the time length in years between seroconversion and the -th measurement of the -th individual after the infection. We construct the following additive model;

the partially linear additive models instead of additive model because of the binaray variable, but we not select the linear component. using our procedure, we wang to ensure which is linear component and which is zero in the non-parametirc function. For implement our procedure, linear transformation be used to the variable. The result of our procedure select the is zero function and select the is a linear function, is a non-parametric. As shown in Figure 1, we see that the mean baseline CD4 percentage of the population

depletes rather quickly at the beginning of HIV infection, but the rate of depletion appears to be slowing down at four years after the infection. This result is the same as before [13] .

5. Concluding Remark

In summary, we present a two-fold penalty variable selection procedure in this paper, which can select linear component and significant covariate and estimate unknown coefficient function simultaneously. The simulation study shows that the proposed model selection method is consistent with both variable selection and linear components selection. Besides, being theoretically justified, the proposed method is easy to understand and straightforward to implement. Further study of the problem is how to use the multi-fold penalty to solve the model selection and variable selection in generalized additive partial linear models with longitudinal data.

Acknowledgements

Liugen Xue’s research was supported by the National Nature Science Foundation of China (11171012), the Science and Technology Project of the Faculty Adviser of Excellent PhD Degree Thesis of Beijing (20111000503) and the Beijing Municipal Education Commission Foundation (KM201110005029).

References

Appendix: Proofs of Theorems

For convenience and simplicity, let denote a positive constant that may be different at each appearance throughout this paper. Before we prove our main theorems, we list some regularity conditions that are used in this paper.

Lemma 1. Under the conditions (A1)-(A6), minimizing the no penalty QIF. Then

Proof: According to [14] , for each, we can get satisfying the condition (4). There exists a constant and a spline function, such that. Using the triangular in equality Therefore, it is su- fficient to show that According to [8] entail that for any. exists sufficiently large. such that therefore Furthermore, for each. There exists a constant. such that

Proof of Theorem 1. Let

be the object function in (2.7), where and, as a special case of no penalty QIF. Let, and, well known result is, we want to show that for large and any, there exist a constant large enough such that

(A1)

As a result, this implies that has a local minimum in the ball. Thus, . Further, the triangular inequality gives To show (A1), For convenience, we assume that is truly nonparametric for is linear for and zero for.

(A2)

Since. Since. We have. If, similarly,. If. These facts imply that and with probability tending to 1. If, , , for. Therefore, when n is large enough,

By the definition of SCAD penalty function, removing the regularizing terms in (A2)

(A3)

with and being the gradient vector and hessian matrix, respectively. Following [8] , and Lemma A1 in supplement, for any with, one has

and

where is the first order derivative of. Therefore, by choosing large enough, the second term on (A3) dominates its first term. therefore (A1) holds when C and n are large enough. This completes the proof of Theorem 1. W

Proof of Theorem 2. We only show part (b), as an illustration and part (a) is similar. Suppose for some, does not represent a linear function. Define to be the same as except that is replaced by its projection onto the subspace { represents a linear function}, we have

As in the proof of Theorem 1, we have and thus with probability ap- proaching 1

(A4)

, with probability tending to 1. by the definition of SCAD penalty. Therefore, similar to the proof of Theorem 1, by choosing large enough, the second term on the right had side of (A4) dominates its first term. W

Proof of Theorem 3. For any regularization parameters, we denote the estimator of two fold penalty, and denote by the minimizer when the optimal sequence of regularization parameters is chosen. There are four separate cases to consider

CASE 1: represents a linear component for some. Similar to the proof of Theorems 1 and 2, we have

Since true not linear and is consistent in model selection, is bounded away form zero, thus for any, with probability tending to 1 and the SIC cannot select such.

CASE 2: is zero for some. The proof is very similar with CASE 1 and therefore omitted.

CASE 3: represents a nonlinear component for some. Here when considering CASE 3, we implicity exclude all previous cases that no underfitting cases. is the estimator of minimizing the no penalty

QIF (2.6) Thus and with probability tending to 1. W

CASE 4: is nonzero for. The case is similar to case 3. Thus the proof is omitted.