Received 23 January 2015; accepted 11 February 2015; published 15 February 2015

ABSTRACT

Fisher [1] proposed a simple method to combine p-values from independent investigations without using detailed information of the original data. In recent years, likelihood-based asymptotic methods have been developed to produce highly accurate p-values. These likelihood-based methods generally required the likelihood function and the standardized maximum likelihood estimates departure calculated in the canonical parameter scale. In this paper, a method is proposed to obtain a p-value by combining the likelihood functions and the standardized maximum likelihood estimates departure of independent investigations for testing a scalar parameter of interest. Examples are presented to illustrate the application of the proposed method and simulation studies are performed to compare the accuracy of the proposed method with Fisher’s method.

Keywords:

Canonical Parameter, Fisher’s Expected Information, Modified Signed Log-Likelihood Ratio Statistic, Standardized Maximum Likelihood Estimate Departure

1. Introduction

Supposed that 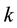independent investigations are conducted to test the same null hypothesis and the p-values are respectively. Fisher [1] proposed a simple method to combine these p-values to obtain a single p-value 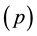without using the detailed information concerning the original data nor knowing how these p-values were obtained. His methodology is based on the following two results from distribution theories:

1) If is distributed as Uniform(0, 1), then 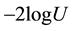is distributed as Chi-square with 2 degrees of freedom

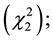
2) If 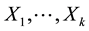are independently distributed as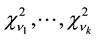, then 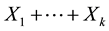is distributed as.

Since 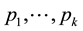are independently distributed as Uniform(0, 1), then the combined p-value is

(1)

For illustration, Fisher [1] reported the p-values of three independent investigations: 0.145, 0.263 and 0.087. Thus the combined p-value is

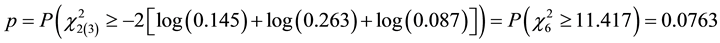
which gives moderate evidence against the null hypothesis. Fisher [1] described the procedure as a “simple test of the significance of the aggregate”.

As an illustrative example is the study of rate of arrival. It is common to use a Poisson model to model the number of arrivals over a specific time interval. Let 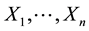be the number of arrivals in n consecutive unit time intervals and denote be the total number of arrivals over the n consecutive unit time intervals. Moreover, let be the rate of arrival in an unit time interval. We observed a total of 14 arrivals over 20 consecutive unit time intervals. In other words, and we are interested in assessing. Then the null distribution of is Poisson (20) and, based on the observed, the mid-p-value is

An alternate way of investigating the rate of arrival over a period of time is by modeling the time to first arrival, T with the exponential model with rate. We observed, and, again, we are interested in assessing. Then the null distribution of is the exponential with rate 1, and, based on the observed, the p-value is

By Fisher’s way of combining the p-values, we have

which gives strong evidence that is greater than 1.

In recent years, many likelihood-based asymptotic methods have been developed to produce highly accurate p-values. In particular, both the Lugannani and Rice’s [2] method and the Barndorff-Nielsen’s [3] [4] method produced p-values which have third-order accuracy, i.e. the rate of convergence is. Fraser and Reid [5] showed that both methods required the signed log-likelihood ratio statistic and the standardized maximum likelihood estimate departure calculated in the canonical parameter scale. In this paper, we proposed a method to combine likelihood functions and the standardized maximum likelihood estimates departure calculated in the canonical parameter scale obtained from independent investigations to obtain a combined p-value.

In Section 2, a brief review of the third-order likelihood-based method for a scalar parameter of interest is presented. In Section 3, the relationship between the score variable and the locally defined canonical parameter is determined. Using the results in Section 3, a new way of combining likelihood information is proposed in Section 4. Examples and simulation results are presented in Section 5 and some concluding remarks are recorded in Section 6.

2. Third-Order Likelihood-Based Method for a Scalar Parameter of Interest

Fraser [6] showed that for a sample from a canonical exponential family model with log-likelihood function

where

and is the scalar canonical parameter of interest. The p-value function can be approximated with third-order accuracy using either the Lugannani and Rice [2] formula

(2)

or the Barndorff-Nielsen [3] [4] formula

(3)

where is the signed log-likelihood ratio statistic

(4)

is the standardized maximum likelihood departure calculated in the canonical parameter scale:

(5)

is the maximum likelihood estimate of satisfying, and

is the observed information evaluated at. Jensen [7] showed that (2) and (3) are asymptotically equivalent up to third-order accuracy. In literature, there exists many applications of these methods, for example, see Brazzale et al. [8] .

Fraser and Reid [5] [9] generalized the methodology to any model with log likelihood function. They defined the locally defined canonical parameter be

(6)

where

(7)

is the rate of change of with respect to the change of at, and is a pivotal quantity. Define be the score variable satisfying

(8)

with being the maximum likelihood estimate of obtained from at the observed data point. The signed log-likelihood ratio statistic r is

(9)

and the standardized maximum likelihood departure re-calibrated in the scale is

Since, by applying the chain rule in differentiation, we have

where. Therefore, can be written as

(10)

Applications of the general method discussed above can be found is Reid and Fraser [10] and Davison et al. [11] .

Note that in (7) can be viewed as the sensitivity direction and is examined in Fraser et al. [12] for the study of the sensitivity analysis of the third-order method. And gives the rate of change of the score variable with respect to the change of at the observed data point in the tangent exponential model.

3. Relationship between the Score Variable and the Locally Defined Canonical Parameter

In Bayesian analysis, Jeffreys [13] proposed to use the prior density which is proportional to the square root of the Fisher’s expected information. This prior is invariant under reparameterization. In other words, the scalar parameter

yields an information function that is constant in value. Since Fisher’s expected information might be difficult to obtain, we can approximate it by the observed information evaluated at the maximum likelihood estimate which is

Hence, is approximately invariant under reparameterization.

Fraser et al. [12] showed that

(11)

is a pivotal quantity to the second-order. A change of variable from the maximum likelihood estimate of locally defined canonical parameter to the score variable for the first integral of (11) yields

(12)

which relates the score varaible to the locally defined canonical parameter. Taking the total derivative of (12), and evaluate at the observed data point, we have

Moreover, at,

Therefore, the rate of change of the score variable with respect to the change of the locally defined canonical parameter at the observed data point is

(13)

This describes how the locally defined canonical parameter moves the score variable.

4. Combining Likelihood Information

Assume we have independent investigations, each of them is used to obtain inference concerning a scalar parameter. Denote the log-likelihood function for the investigation be and the corresponding canonical parameter is. Note that if is not explicitly available, we can use the locally defined canonical variable as obtain from (9). The combined log-likelihood function is

and hence the maximum likelihood estimate of can be obtained. Therefore, the signed log-likelihood function can be calculated from (12).

From (13), the rate of change of the score variable from the investigation with respect to the corresponding canonical paramter at the observed data from the investigation is

(14)

where

Hence, the combined canonical parameter is

(15)

The standardized maximum likelihood departure based on the combined canonical parameter can be calculated from (5). Thus, a new p-value can be obtained from the combined log-likelihood function and the combined canonical parameter using the Lugannani and Rice formula or the Barndorff-Nielsen formula.

5. Examples

In this section, we first revisit the rate of arrival problem discussed in Section 1 and show that the proposed method gives results that is quite different from the results obtained by the Fisher’s way of combining p-values. Then simulation studies are performed to compare the accuracy of the proposed method with the Fisher’s method for the rate of arrival problem. Moreover, two well-known models: scalar canonical exponential family model and normal mean model, are examined. It is shown that, theoretically, the proposed method gives the same results as obtained by the third-order method that was discussed in Fraser and Reid [5] and DiCiccio et al. [14] , respectively.

5.1. Revisit the Rate of Arrival Problem

From the first investigation discussed in Section 1, the log-likelihood function for the Poisson model is

where is the canonical parameter. We have

Moreover, from the second investigation discussed in Section 1, the log-likelihood function for the exponential model is

where is the canonical parameter. We have

The combined log-likelihood function is

and we have

Therefore,

and from (17) we have and. Thus, the combined locally defined canonical parameter is

Hence, is obtained from (12) using the combined log-likelihood function. Since the signed loglikelihood ration statistic is asymptotically distributed as a standard normal distribution, the p-value obtained from the signed log-likelihood ratio method is 0.0565. It is well-known that the signed log-likelihood ratio method has only first order accuracy. From (8) using the combined locally defined canonical parameter, we have. Finally, the p-value obtained by the Lugannani and Rice formula and by the Barndorff-Nielsen formula is 0.0600, which is less certain about the evidence that is greater than 1 as suggested by the result from Fisher’s way of combining of p-values. Note that in literature, there are many detailed studies comparing the accuracy of the first order and third order methods (see Barndorff-Nielsen [4] , Fraser [6] , Jensen [7] , Brazzale et al. [8] , and DiCiccio et al. [14] ). Thus, in this paper, we will not compare the signed log-likelihood ratio method and the proposed method.

Figure 1 plot obtained from Fisher’s method, Lugannani and Rice method and Barndorff- Nielsen method. From the plot, it is clear that the two proposed methods give almost identical results, which are very different from the results obtained by the Fisher’s method.

5.2. Simulation Study

Simulation studies are performed to compare the three methods discussed in this paper. We examine the rate of arrival problem that was discussed in Section 1. For each combination of, we

1) generate from Poisson, and from exponential

2) calculate p-values obtained by the three methods discussed in this paper;

3) record if the p-value is less than a preset value

4) repeat this process times.

Finally, report the proportion of p-values that is less than and this value, sometimes, is referred to as the simulated Type I errors. For an accurate method, the result should be close to. The simulated standard error of this process is.

Table 1 recorded the simulated Type I errors obtained by the Fisher’s method (Fisher), Lugannani and Rice method (LR) and Barndorff-Nielsen method (BN). Results from Table 1 illustrated that the proposed methods are extremely accurate as they are all within 3 simulated standard errors. And the results by the Fisher’s method are not satisfactory as they are way larger than the prescriped values.

5.3. Scalar Canonical Exponential Family Model

Consider independent investigations from canonical exponential family model with density

where is the scalar canonical parameter of interest and is the minimal sufficient statistic for the model.

From the above model, we have. The log-likelihood function and its corresponding derivatives are

where. Hence has to satisfy, and the observed information evaluated at is. The combined log-likelihood function is

and the log-likelihood ratio statistic obtained from the combined log-likelihood function can be obtained from (12). Moreover, from (17), we have

and hence the combined canonical parameter is

The maximum likelihood departure in the combined canonical parameter space is

with the observed information evaluated at being

and thus,

which is the same as directly applying the third-order method to the canonical exponential family model with being the canoncial parameter as discussed in Fraser and Reid [5] .

5.4. Normal Mean Model

Consider independent investigations from normal mean model with density

where is the mean parameter of interest. The pivotal quantity is. Hence, , and

with and. The combined log-likelihood function is

with and. From (17), we have and, therefore the combined canonical parameter is

and. Finally, from Equation (12), the signed log-likelihood ratio statistic is

and the standardized maximum likelihood departure calculated in the locally defined canonical parameter scale can be obtained from Equation (8) and is

These are exactly the same as those obtained in DiCiccio et al. [14] .

6. Conclusion

In this paper, a method is proposed to obtain a p-value by combining the likelihood functions and the standardized maximum likelihood estimates departure calculated in the canonical parameter space of independent investigations for testing a scalar parameter of interest. It is shown that for the canonical exponential model and the normal mean model, the proposed method gives exactly the same results as using the joint likelihood function. Moreover, for the rate of arrival problem, the proposed method gives very different results from the results obtained by the Fisher’s way of combining p-values. And simulation studies illustrate that the proposed method is extremely accurate.

Acknowledgements

This research was supported in part by and the National Sciences and Engineering Research Council of Canada.

References