Open Journal of Statistics
Vol.04 No.09(2014), Article ID:50507,5 pages
10.4236/ojs.2014.49068
Statistical Tools for Estimation of Threshold Values at Data Classification Task Solution
V. V. Glinskiy, L. K. Serga, E. Yu. Chemezova, K. A. Zaykov
Department of Statistics, Novosibirsk State University of Economics and Management, Novosibirsk, Russian Federation
Email: s444@ngs.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 July 2014; revised 26 August 2014; accepted 10 September 2014
ABSTRACT
The paper contains a summary of some results of original research total aggregates. The main idea is determining the boundaries of the groups for classification of fuzzy and threshold aggregates using the method of decomposing a mixture of probability distributions. The article presents the experience of partitions of a real aggregate as a finite mixture of probability distributions on private aggregates. Threshold value defined by the boundaries of private aggregates, will match the value of the phenomenon at the intersection of the curves of probability distributions, which extracted from the mixture. The proposed scheme of identification threshold aggregates has found practical application in the research of aggregate of Russian employees by level of payroll and establishing the optimal minimum value monthly wage. The official data of the Federal State Statistics Service were used.
Keywords:
Classification, Threshold Aggregate, Mixture of Probability Distributions

1. Introduction
Issues of statistical investigation of aggregate instability (variability, uncertainty of composition, inconstancy of structure) remained out of focused attention of specialists until recently. Various classifications of aggregates, used in the statistical theory, do not meet the modern requirements completely or make it possible to solve the whole variety of statistical tasks in conditions of increasing turbulence. It defined the necessity for investigation of additional classificatory sections of real aggregates, such as dynamic and threshold (see more detailed data [1] -[5] ).
The threshold classificatory section considers the level of unambiguousness in determination of aggregate limits (individual types) in a statistical investigation of general aggregates. In this regard it is possible to mark out precise, threshold and fuzzy aggregates. Identification of precise, threshold or fuzzy aggregates is equivalent to the solution of a problem of typology of data [1] [2] [6] - [11] .
2. Tools of the Investigation
Threshold sets are such real sets where elements fall into them on the basis of the statistical criteria entered by an artificial way. Determination of threshold values leads to breakdown of initial qualitatively non-uniform aggregate to uniform private aggregates. The general scheme of the statistical investigation of threshold aggregates is presented in Figure 1.
Aggregate of wage workers can be given as an example of threshold aggregates by the size of wage paid. As is known, wage level depends on the minimum wage established in a legislative order. The minimum wage―the size of a monthly salary guaranteed by the state for work of the unskilled worker who completely fulfilled norm of working hours at performance of simple work in normal working conditions; minimum wage [12] . The minimum wage will be a peculiar “threshold” for the whole aggregate, introduced for artificial regulation of labor compensation of population by the state.
Sets, obtained as a result of division of a general aggregate of a set, are subject to certain laws of the development, inherent to elements of this private aggregate. However, in practice, the statistical accounting of elements of a general aggregate occurs identically, considers no features of each private threshold aggregate, resulting in reduction of quality, reliability and accuracy of statistical information.
Taking into consideration mentioned above and subjective nature of determination of limits-thresholds of aggregate (comprehensive justification of its value is not always the case), the researcher faces a challenge of definition of objective rules and criteria of finding of threshold values so that they clearly identify the transitions from one qualitative condition of phenomena to another.
There are many methods and algorithms directed to the solution of this issue; this paper discusses the experience of breakdown of real aggregate to private subaggregates (types), considering the initial one as a final mix of probability distributions. Objective threshold is obtained as a result of division of a mix into its components. Threshold value will correspond to the occurrence size at the intersection of curves probability distributions.
Final mix of distribution refers to a distribution of probabilities representing linear function of some number of components of distributions of probabilities [13] - [15] . Such distributions are used for modeling of aggregates which allegedly contain separate groups of observation or separate groups (types) of elements of aggregate.
Figure 1. The general scheme of the statistical investigation of threshold aggregates.
Initial example of application of such distribution is the distribution mixed from two normal ones and applied by Pearson in 1894 (Equation (1)).
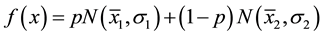 , (1)
, (1)
where ―a share of the first group in the aggregate;
―a share of the first group in the aggregate;
 ―respectively average and mean-square deviation of a variable in the first group;
―respectively average and mean-square deviation of a variable in the first group;
 ―the corresponding values in the second group.
―the corresponding values in the second group.
To solve a problem of distribution of a mix is to construct statistical estimates for a number of components of a mix, their specific weight and parameters that define them, using the available selection of the classified observations taken from general aggregate, which is a mix of private unimodular aggregates of a known parametrical form.
In theoretical option the task of splitting of a mix consists in restoration of components of a mix and mixing function (specific weights) by the given distribution of the whole (i.e. mixed) general aggregate and it is called as a task of identification of components of a mix [14] - [18] .
Considerable number of techniques of division of mixes of distribution is used in applied calculations. Each method has the merits and demerits connected both with complexity of calculations and accuracy of obtained results.
In the current research has been applied the EM algorithm; it is used in mathematical statistics for finding of estimates of maximum likelihood of parameters of probabilistic models, when a model depends on some hidden variables.
The main assumption of the EM algorithm is that the studied set of data can be simulated by means of a linear combination of multidimensional distributions, and the purpose is the assessment of parameters of distribution which maximize logarithmic likelihood function. Each iteration of the algorithm consists of two steps known as E (Expectation step), and M (Maximization step). The expected value of the logarithmic likelihood function of credibility at the first step is based on observed data, and current estimates of parameters are found. This function is maximized at the M-step for obtaining the improved estimates of parameters which increase likelihood. Steps alternate until convergence. Sometimes this algorithm converges very slowly.
3. Real Minimal Monthly Wage as a Threshold Value of Grouping of Wage Workers by Salary
Application of methods of division of mix of distributions was carried out by the example of aggregate of wage workers from sample observation, conducted by the Federal State Statistics Service (Rosstat) in April annually regarding salary [19] . Official data of Rosstat about distribution of number of employees by sizes of wage paid for 2000-2013 were used for the research. All data is presented in Table 1, Figure 2 and Figure 3.
The calculation results show that aggregate-mix is subject to lognormal distribution that in principle corresponds to general notions about the law of distribution of salary of wage workers. The probability of accepting of a null hypothesis for the lognormal law of distribution is on average equals to 84% (used software packages: Microsoft Office Excel, STATISTICA, Wolfram Mathematica).
Accepting as a working hypothesis that a number of distribution by wage, for example for 2011, is deformed by a fixed observation error caused by concealment of wage level.
It will be natural to expect the increased concentration of a number near threshold value (minimum monthly wage) and, respectively, to assume that the left part of the aggregate can be described by one distribution of probabilities, while the right part can be approximated by the other, i.e. this aggregate can be broken down to two groups (private aggregates). The boundary between these groups, in author’s opinion, has to correspond to minimum monthly wage.
Noting that at the subsequent splitting of the mix into aggregate elements it is seen that the mix decomposition to two components with normal and lognormal laws of distribution of probabilities is better.
This situation is most characteristic for 2002, 2004, 2009, 2010, 2011 and 2013. Two distributions-compo- nents are formed in the result of decomposition, the first―the “left” component is approximated by the normal law of distribution. The second―“right” is approximated by logarithmic normal law of distribution.
The first group is formed under the influence of a threshold (minimum wage rate size)―burst of observations near the threshold is observed, the second group corresponds to the economic law of distribution of wage of
Table 1. Distribution of number of employees in the Russian Federation by sizes of wage paid for 2000-2013, in % [19] .
Figure 2. Frequency distribution of employees in the Russian Federation by wage paid in 2000- 2008 [19] .
population. Probabilities of accepting null hypotheses on these distributions are higher than probability of accepting a hypothesis of lognormal distribution of the whole aggregate (92% and 88% respectively).
In summary it can be noted that results of the carried-out calculations, among other things, don’t reject a hypothesis of occurrence of a fixed observation error, which most likely resulted from concealment of wage rates by respondents.
With a view to bring out at least part of the real wage from shadow sector, and to increase accuracy of statistical data, give additional incentive for development of the Russian economy, it is necessary, on author’s opinion, to establish the minimum monthly wage at the level of the value equal to boundary between two aggregates- components, that is to a peculiar “natural” minimum monthly wage. The sizes of the offered (“natural”) and in place (official) minimum monthly wage are entered in Table 2 for comparison.
Figure 3. Frequency distribution of employees in the Russian Federation by wage paid in 2009- 2013 [19] .
Table 2. “Natural” and official minimum monthly wage in the Russian Federation in 2002, 2004, 2009-2011, 2013.
4. Concluding Remarks
This paper proposes a scheme of identification and the statistical research threshold aggregates using the method of decomposing a mixture of probability distributions. The scheme of identification threshold aggregates has found practical application in the research of aggregate of Russian employees by level of payroll. Research has proven that this aggregate of employees is heterogeneous and represents the final mixture of two probability distributions. The original aggregate was divided into the private aggregates by EM-algorithm. The value of the phenomenon at the intersection of the curves of probability distributions extracted from the mixture corresponds to the threshold value determined by the boundaries of private aggregates. This value is set as a logical science-based minimum wage of employees in the Russian Federation. This will bring some of the real wages of the informal sector and provide an additional incentive for the development of the economy.
Acknowledgements
The paper was performed according to the results of State Task research of perform state works in the field of scientific activity (the project “Development of the theory and methodology of statistical research of unstable aggregates”, No 2014/142).
References
- Glinskiy, V.V. (2008) Statistical Methods to Support Management Decisions: Monograph. Publishing NSUEM, Novosibirsk. (Statisticheskie metody podderzhki upravlencheskih reshenij).
- Glinskiy, V.V. (2008) Mystical Small Business Statistics. Problems of Statistical Study of Turbulent Sets. ECO, 9, 51-61.
- Glinskiy, V.V. and Serga, L.K. (2011) Statistics of the XXI Century. Vector of Development. Vestnik NSUEM, 1, 108-118.
- Glinskiy, V.V. and Serga, L.K. (2011) On State Regulation of Small Business in Russia National Interests: Priorities and Safety, 19, 2-8.
- Serga, L.K. (2013) Research of Innovation Activity of Small and Medium-Sized Business. Vestnik NSUEM, 1, 112- 140.
- Chemezova, E.Yu. (2010) Typology of RF Subjects by Level of Social and Economic Development. Vestnik NSUEM, 1, 171-176.
- Glinskiy, V.V. and Serga, L.K. (2009) Nonstable Aggregates: Conceptual Foundation of Statistical Study Methodology. Vestnik NSUEM, 2, 137-142.
- Glinskiy, V.V. and Chemezova, E.Yu. (2012) On Convergence of Main Concepts of Typology of Social-Economic Studies Data. Vestnik NSUEM, 2, 67-73.
- Serga, L.K. (2012) On the Approach to the Definition of the Threshold Values in the Solution of Classification. Vestnik NSUEM, 1, 54-60.
- Serga, L.K., Nikiforova, M.I., Rumynskaya, E.S. and Khvan, M.S. (2012) Applied Use of Portfolio Analysis Methods. Vestnik NSUEM, 3, 146-158.
- Serga, L.K. (2013) On Approaches to Solution of the Problem of Fuzzy Aggregations. Vestnik NSUEM, 3, 83-91.
- (2014) Labor Code of the Russian. Art. 133. In: Consultant plus Version Professional. (Trudovoj kodeks Rossijskoj Federacii). http://www.consultant.ru/popular/tkrf/
- Orlov, A.I. (2004) Non-Numeric Statistics. MZ-Press, Moscow. (Neparametricheskaja statistika).
- Tu, J. and Gonzalez, C. (1978) Principles of Pattern Recognition: Monograph. Mir, Moscow.
- Zaykov, K.A. (2013) Research of the Threshold Aggregates by Decomposition of Mixtures Distributions. Scientific Works of the Free Economic Society of Russia, 172, 192-202.
- Everitt, B.S. (2010) Large Dictionary of Statistics. 3rd Edition, Prospect, Moscow. (Bol’shoj slovar’ po statistike).
- Venetskiy, I.G. and Venetskiy, V.I. (1974) Basic Mathematical and Statistical Concepts and Formulas in the Economic Analysis. Statistics, Moscow. (Osnovnye matematiko-statisticheskie ponjatija i formuly v jekonomicheskom analize).
- Wentzel, E.S. and Ovcharov, L.A. (2000) Probability Theory and Its Engineering Applications. Textbook. Manual for Technical Schools. 2nd Edition, Higher School, Moscow. (Teorija verojatnosti i ee inzhenernye prilozhenija).
- Official Website of the Federal State Statistics Service. http://www.gks.ru





