Open Journal of Statistics
Vol.04 No.08(2014), Article ID:49945,9 pages
10.4236/ojs.2014.48058
Modified Maximum Likelihood Estimation in Autoregressive Processes with Generalized Exponential Innovations
Bernardo Lagos-Álvarez1, Guillermo Ferreira1, Emilio Porcu2
1Department of Statistics, Universidad de Concepción, Concepción, Chile
2Department of Mathematics, University Federico Santa María, Valparaíso, Chile
Email: bla@udec.cl, gferreir@udec.cl, emilio.porcu@usm.cl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2014; revised 8 July 2014; accepted 26 July 2014
ABSTRACT
We consider a time series following a simple linear regression with first-order autoregressive errors belonging to the class of heavy-tailed distributions. The proposed model provides a useful generalization of the symmetrical linear regression models with independent error, since the error distribution covers both correlated innovations following a Generalized Exponential distribution. Furthermore, we derive the modified maximum likelihood (MML) estimators as an efficient alternative for estimating model parameters. Finally, we investigate the asymptotic properties of the proposed estimators. Our findings are also illustrated through a simulation study.
Keywords:
Autoregressive Time Series Model, Maximum Likelihood, Modified Maximum Likelihood, Least Squares, Generalized Exponential

1. Introduction
The common model for a stationary time series is the stationary and invertible autoregressive model of order  where the usual assumption is that the innovations
where the usual assumption is that the innovations 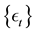 are identically and independently distributed (IID) according to a Gaussian distribution with zero mean and variance
are identically and independently distributed (IID) according to a Gaussian distribution with zero mean and variance .
.
Recent and past literatures agree in that the assumption of Gaussianity is a way too restrictive in order to deal with applications (see [1] and [2] with the references therein). On the other hand, [3] assumed 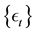 has a Laplace distribution and computes the maximum likelihood (ML) estimators by using iterative methods. [2] have used the modified likelihood function proposed by [4] which is based on censored normal samples [5] and have studied the robustness properties of the resulting estimators. In this context, [6] generated non-Gaussian distributions through transformations of a Gaussian variate.
has a Laplace distribution and computes the maximum likelihood (ML) estimators by using iterative methods. [2] have used the modified likelihood function proposed by [4] which is based on censored normal samples [5] and have studied the robustness properties of the resulting estimators. In this context, [6] generated non-Gaussian distributions through transformations of a Gaussian variate.
[7] considered the Huber M-estimation, which is valid under heavy-tailed symmetric distributions, and uses different forms of contaminated Gaussian to compute the influence functionals (IF) of parameter estimates and gross-error sensitivity for the IF. In this context, [8] and [9] have studied the rate of convergence of the least squares (LS) estimators. It may be noted that M-estimation is not valid for skewed distributions, and has the problem of inefficient estimates for short-tailed symmetric distributions; this has been widely shown by [1] in the classical framework of IID observations.
[10] obtained approximations to some likelihood functions in the context of state space models as considered by [11] . Besides, [12] considered an asymmetric Laplace distribution for the innovations of an autoregressive and moving average model and of a generalized autoregressive conditional heteroscedastic model.
The main proposal of our paper is based on the use of modified likelihood as introduced by [13] [14] and [15] under the framework of IID observations, in order to estimate the parameters in the context of simple linear regression with stationary and invertible autoregressive errors of order one with innovations represented by Generalized Exponential distribution; for more details on these distributions the reader refers to [16] . This method is notorious for giving asymptotically fully efficient estimators (for example, see [17] -[20] ).
The outline of the paper is as follows. In Section 2 we define the regression linear model with autoregressive errors, where the underlying distribution of the innovations is a Generalized Exponential distribution. In Section 3 we propose the MML estimators as a powerful methodology to deal with ML estimators which are intractable in the case of a Generalized Exponential distribution. In Section 4 we study the asymptotic properties of the proposed estimators. The main advantages of the proposed estimators are discussed via simulation studies in Section 5. Finally discussions and observations appear in Section 6 of the proposed model and the specific numerical results, attaching an Appendix which displays the details of asymptotic results.
2. The Model
We denote 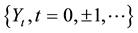 a time series and the following model
a time series and the following model
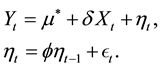 (1)
(1)
where Xt is the value of a fixed design variable X at time t, 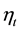 is the error, assumed to be modeled through a non-Gaussian stationary autoregressive model,
is the error, assumed to be modeled through a non-Gaussian stationary autoregressive model,  is a constant,
is a constant, 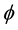 is the autoregressive coefficient, with
is the autoregressive coefficient, with , and
, and 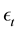 is the innovation, distributed according to a Generalized Exponential distribution (GEd), given by
is the innovation, distributed according to a Generalized Exponential distribution (GEd), given by
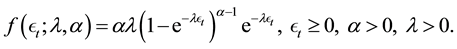 (2)
(2)
The corresponding cumulative distribution function is given by
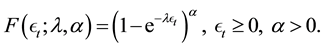 (3)
(3)
Notably, 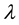 and
and 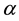 play, respectively, the role of scale and shape parameters. The
play, respectively, the role of scale and shape parameters. The  has a similar form to the Gamma and Weibull distributions. See the survey in [21] for some recent developments on GEd, distributions.
has a similar form to the Gamma and Weibull distributions. See the survey in [21] for some recent developments on GEd, distributions.
3. Modified Maximum Likelihood Estimators
The model in Equation (1) can be written as

or

whit





where




The log-likelihood is given by

For convenience we introduce at this point the following reparameterization: 



where 


Now



Also note that if we consider the parameter 


For notational simplicity, let us write



The likelihood equations are expressions in terms of intractable functions
In order to obtain efficient closed form estimators, we consider Tiku’s method of modified likelihood estimation, which is by now well established, see [22] (Chapter 6). For given values of







A standard Taylor expansion of 


where 



where 



where 




Plugging (14) into (13), we obtain the approximated derivative of the log-likelihood function for




The zeros of the above system of equations are the MML estimators of







Then, from the Equations (17) and (19) we get
Defining the n-dimensional vectors, 







where
and
Furthermore, note that setting the expression for 


We note that the coefficients




Moreover



observe that these estimates involve the 
These facts suggest that it is possible to obtain MML estimators of 



where



We suggest the following routine for the numerical computation of the MML estimator. Initialize with 

Step 0. Set 
Step 1. Get 





Step 2. Evaluate the expressions (15)-(17) in 
Step 3. Get from (7) the initial estimates for the



Step 4. With the values of Step 3, get 


Step i. Get 





The steps are repeated until convergence is achieved.
Remark. The stopping criteria is given by
4. Asymptotic Equivalence and Efficiency
The asymptotic equivalence of MML and ML estimators is based on the fact that 


On the other hand, if we know the values of 






standard Taylor expansion in a neighborhood of 
Using the results (5.7.5), p. 115 of [25] and Lemma 1 in the Appendix, we show that 

Furthermore, if we know the values of 




knowledge of the values of 

with



The asymptotic behavior of variance for 




Analogously, we have
where 




Table 1. The simulated values of mean, bias square and mean square error of the LS estimators 


5. Simulation Study
In order to have some indications of the robustness aspects of the MML estimates of




where
1) 
2) 
3) 
4) 
5) 
Without loss of generality, we have considered the parameter b as a constant value given by b = −1 and −2. The summaries of Monte Carlo study for



6. Conclusion
In this paper, we have studied a regression linear model with first-order autoregressive errors belonging to a class of asymmetric distributions; more specifically the underlying distribution for the innovations is a Generalized Exponential distribution. We have developed a complete asymptotic theory for the MML estimators in these models. In addition, we have shown that the MML estimators are robust and efficient, as depicted by the numerical study presented in Section 5 for the AR(1) GE model. We thus claim that the MML estimator is a very good alternative to estimate autoregressive models with asymmetric innovations (see [26] and [27] , among others as example). The R codes may be obtained from the authors upon request in order to analyze such models.
Acknowledgements
The first author would like to thank for the support from DIUC 213.014.022-1.0, established by the Universidad de Concepción. The second author gratefully acknowledges the financial support from ECOS-CONICYT C10E03, established by the Chilean Government and DIUC 213.014.021-1.0 from the Universidad de Concepción and the third author was supported by Fodecyt grant 1130647.
References
- Tiku, M.L., Tan, W.Y. and Balakrishnan, N. (1986) Robust Inference. Marcel Dekker, Inc., New York.
- Tan, W.Y. and Lin, V. (1993) Some Robust Procedures for Estimating Parameters in an Autoregressive Model. Sankhya B, 55, 415-435.
- Damsleth, E. and El-Shaarawi, A.H. (1989) ARMA Models with Double Exponentially Distributed Noise. Journal of the Royal Statistical Society B, 51, 61-69.
- Tiku, M.L. (1980) Robustness of MML Estimators Based on Censored Samples and Robust Test Statistics. Journal of Statistical Planning and Inference, 4, 123-143. http://dx.doi.org/10.1016/0378-3758(80)90002-6
- Tan, W.Y. (1985) On Tiku’s Robust Procedure―A Bayesian Insight. Journal of Statistical Planning and Inference, 11, 329-340. http://dx.doi.org/10.1016/0378-3758(85)90038-2
- Swift, A.L. (1995) Modelling and Forecasting Time Series with a General Non-Normal Distribution. Journal of Forecasting, 14, 45-66. http://dx.doi.org/10.1002/for.3980140105
- Martin, R.D. and Yohai, V.J. (1986) Influence Functionals for Time Series. Annals of Statistics, 14, 781-818. http://dx.doi.org/10.1214/aos/1176350027
- Bhansali, R.J. (1997) Robustness of the Autoregressive Spectral Estimate for Linear Process with Infinite Variance. Journal Time Series Analysis, 18, 213-229. http://dx.doi.org/10.1111/1467-9892.00047
- Davis, R.A. and Resnick, S. (1986) Limit Theory for the Sample Covariance and Correlation Functions of Moving Averages. Annals of the Institute of Statistics, 14, 533-558. http://dx.doi.org/10.1214/aos/1176349937
- Durbin, J. and Koopman, S.J. (1997) Monte Carlo Maximum Likelihood Estimation for Non-Gaussian State Space Models. Biometrika, 84, 669-684. http://dx.doi.org/10.1093/biomet/84.3.669
- Kitagawa, G. (1987) Non-Gaussian State-Space Modelling of Nonstationary Time Series (with Discussion). Journal of the American Statistical Association, 82, 1032-1063.
- Trindade, A.A. and Zhu, Y. (2010) Time Series Models with Asymmetric Laplace Innovations. Journal of Statistical Computation and Simulation, 80, 1317-1333.
- Tiku, M.L. (1967) Estimating the Mean and Standard Deviation from Censored Normal Samples. Biometrika, 54, 155- 165. http://dx.doi.org/10.2307/2283834
- Tiku, M.L. (1968) Estimating the Parameters of Log-Normal Distribution from Censored Samples. Journal of the Ame- rican Statistical Association, 63, 134-140. http://dx.doi.org/10.2307/2283834
- Tiku, M.L. and Suresh, R.P. (1992) A New Method of Estimation for Location and Scale Parameters. Journal of Statistical Planning and Inference, 30, 281-292. http://dx.doi.org/10.1111/1467-842X.00072
- Gupta, R.D. and Kundu, D. (1999) Generalized Exponential Distributions. Australian and New Zealand Journal of Statistics, 41, 173-188. http://dx.doi.org/10.1111/1467-842X.00072
- Vaughan, D.C. and Tiku, M.L. (2000) Estimation and Hypothesis Testing for a Non-Normal Bivariate Distribution with Applications. Journal of Mathematical and Computer Modelling, 32, 53-67. http://dx.doi.org/10.1016/S0895-7177(00)00119-9
- Bhattacharyya, G.K. (1985) The Asymptotics of Maximum Likelihood and Related Estimators Based on Type II Censored Data. Journal of the American Statistical Association, 80, 398-404. http://dx.doi.org/10.1080/01621459.1985.10478130
- Tiku, M.L. (1970) Some Notes on the Relationship between the Distribution of Central and Non-Central F. Biometrika, 57, 175-179. http://dx.doi.org/10.1093/biomet/57.1.175
- Tiku, M.L. (1970) Monte Carlo Study of Some Simple Estimators in Censored Normal Samples. Biometrika, 57, 207- 210.
- Gupta, R.D. and Kundu, D. (2007) Generalized Exponential Distribution: Existing Methods and Some Recent Developments. Journal of Statistical Planning and Inference, 137, 3537-3547. http://dx.doi.org/10.1016/j.jspi.2007.03.030
- Balakrishnan, N. and Cohen, A.C. (1991) Order Statistics and Inference. Academic Press, Waltham.
- Raqab, M.Z. and Ahsanullah, M. (2001) Estimation of Location and Scale Parameters of Generalized Exponential Distribution Based on Order Statistics. Journal of Statistical Computation and Simulation, 69, 109-124.
- Kendall, M.G. and Stuart, A. (1979) The Advanced Theory of Statistics. Charles Griffin, London.
- Tiku, M.L. and Akkaya, A.D. (2004) Robust Estimation and Hypothesis Testing. New Age International (P) Publishers, New Delhi, 337.
- Wong, W.K. and Bian, G. (2005) Estimating Parameters in Autoregressive Models with Asymmetric Innovations. Statistics and Probability Letters, 71, 61-70. http://dx.doi.org/10.1016/j.spl.2004.10.022
- Tiku, M.L., Wong, W.K. and Bian, G. (1999) Time Series Models with Asymmetric Innovations. Communications in Statistics―Theory and Methods, 28, 1331-1360. http://dx.doi.org/10.1080/03610929908832360
Appendix
Lemma 1. Let





where 

Proof
Lemma 2. For the process 




Proof is deduced by using the moment generating function of

(see [21]). Moreover, for the
and for

































