Open Journal of Statistics
Vol.4 No.4(2014), Article
ID:47086,8
pages
DOI:10.4236/ojs.2014.44029
A Class of Estimators for Population Ratio in Simple Random Sampling Using Variable Transformation
A. C. Onyeka, V. U. Nlebedim, C. H. Izunobi
Department of Statistics, Federal University of Technology, Owerri, Nigeria
Email: aloyonyeka@yahoo.com, uchenlebedim@yahoo.com, chiyeaka2007@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2014; revised 19 May 2014; accepted 8 June 2014
Abstract
This paper is an extension and generalization of the study carried out by [1] on the estimation of the population ratio (R) of the population means of two variables (y and x) under Simple Random Sampling (SRS) scheme, using a variable transformation of the auxiliary variable, x. All the six estimators proposed by [1] are easily identified as special cases of the proposed class of estimators. Asymptotic properties of the proposed class of estimators are derived theoretically and subsequently verified using empirical illustrations. Some of the proposed estimators are found to have relatively large gains in efficiency over the customary ratio estimator, ![]() for the given data set.
for the given data set.
Keywords:Variable Transformation, Ratio, Product and Regression-Type Estimators, Mean Squared Error

1. Introduction
Let n units be drawn from a population of N units using simple random sampling without replacement (SRSWOR) method, and let 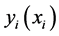 be ith observations on the study (auxiliary) variable. Reference [2] considered the following variable transformation of the auxiliary variable, x, under the simple random sampling scheme.
be ith observations on the study (auxiliary) variable. Reference [2] considered the following variable transformation of the auxiliary variable, x, under the simple random sampling scheme.
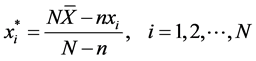 , (1)
, (1)
Other authors who have used the transformation (1) under the simple random sampling scheme include [3] -[5] , while [6] employed the transformation for mean estimation under the post-stratified sampling scheme. An expression of the (transformed) sample mean associated with the variable transformation in (1) is given as:
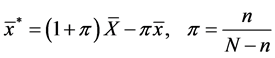 (2)
(2)
where  is the sample (population) mean of the auxiliary variable, x.
is the sample (population) mean of the auxiliary variable, x.
Using the variable transformation (1), the following six estimators for the estimation of the population ratio, R, were proposed by [1] in simple random sampling without replacement (SRSWOR) scheme:
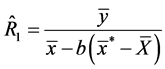 (regression-type estimator based on
(regression-type estimator based on![]() ) (3)
) (3)
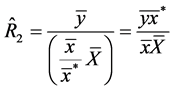 (ratio-type estimator based
(ratio-type estimator based![]() ) (4)
) (4)
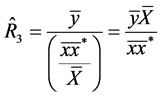 (product-type estimator based on
(product-type estimator based on ![]() or
or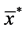 ) (5)
) (5)
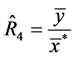 (simple ratio estimator based on
(simple ratio estimator based on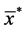 ) (6)
) (6)
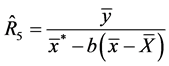 (regression-type estimator based on
(regression-type estimator based on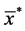 ) (7)
) (7)
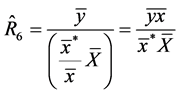 (ratio-type estimator based on
(ratio-type estimator based on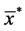 ) (8)
) (8)
where 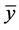 is the sample mean of the study variable, y, and b is a suitable constant, often chosen to be close to the population regression coefficient of y on x. In the present study, we introduce a class of estimators, which is both a generalization and an extension of the estimators (3) to (8), proposed by [1] . We observe that apart from the customary ratio estimator,
is the sample mean of the study variable, y, and b is a suitable constant, often chosen to be close to the population regression coefficient of y on x. In the present study, we introduce a class of estimators, which is both a generalization and an extension of the estimators (3) to (8), proposed by [1] . We observe that apart from the customary ratio estimator, 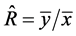 , other estimators of the population ratio, R, in literature, like those proposed by [7] -[9] , often require additional information on some auxiliary variables, and consequently involving extra funds. Reference [1] argued that such extra costs could be avoided by using variable transformation of the already observed auxiliary variable, x. Accordingly, cost reduction in constructing estimators of the population ratio, R, is a strong motivation for the general class of estimators, which the present study seeks to introduce in the estimation of population ratio, R, using variable transformation.
, other estimators of the population ratio, R, in literature, like those proposed by [7] -[9] , often require additional information on some auxiliary variables, and consequently involving extra funds. Reference [1] argued that such extra costs could be avoided by using variable transformation of the already observed auxiliary variable, x. Accordingly, cost reduction in constructing estimators of the population ratio, R, is a strong motivation for the general class of estimators, which the present study seeks to introduce in the estimation of population ratio, R, using variable transformation.
2. The Proposed Class of Estimators
Following [1] , we propose a class of estimators of the population ratio (R) of the population means of two variables (y and x) under simple random sampling without replacement (SRSWOR) scheme, using variable transformation of the auxiliary variable, x, as:
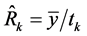 (9)
(9)
where
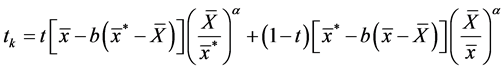 (10)
(10)
and t, b, Table 1 shows some particular cases of the proposed class of estimators Table 1. Special cases of the proposed class of estimators,  are suitably chosen constants, whose appropriate choices would eventually result in a wide range of estimators of the population ratio, R.
are suitably chosen constants, whose appropriate choices would eventually result in a wide range of estimators of the population ratio, R. ![]() .
. 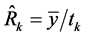 , including
, including ,
, 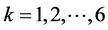 proposed by [1]
proposed by [1] in (10).
in (10).
Here, the naming of the proposed class of estimators, 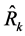 , is based on (10) or the denominator,
, is based on (10) or the denominator, 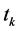 , of the proposed ratio estimator,
, of the proposed ratio estimator,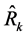 . The customary ratio estimator,
. The customary ratio estimator, 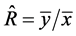 is a ratio of two sample means, namely the sample means of the study and auxiliary variables. The sample mean
is a ratio of two sample means, namely the sample means of the study and auxiliary variables. The sample mean ![]() in the denominator is an estimate of the population mean,
in the denominator is an estimate of the population mean, ![]() , of the auxiliary variable. With variable transformation, we replace the sample mean
, of the auxiliary variable. With variable transformation, we replace the sample mean ![]() in the denominator of
in the denominator of 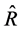 by the expression
by the expression 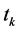 in (10). The expression
in (10). The expression 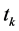 actually generates a kind of different estimators of the population mean
actually generates a kind of different estimators of the population mean  based on 1) the sample mean
based on 1) the sample mean ![]() of the auxiliary variate,
of the auxiliary variate, 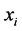 , or 2) the sample mean
, or 2) the sample mean 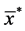 of the transformed auxiliary variable,
of the transformed auxiliary variable, ![]() , or 3) a combination of both 1) and 2) above. For instance, choosing
, or 3) a combination of both 1) and 2) above. For instance, choosing ![]() and
and ![]() in (10) reduces
in (10) reduces 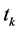 to
to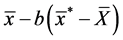 , which is a kind of a regression-type estimator of
, which is a kind of a regression-type estimator of ![]() based on the sample mean
based on the sample mean ![]() of the auxiliary variate,
of the auxiliary variate,  , while choosing
, while choosing
![]() and
and ![]() in (10) reduces
in (10) reduces 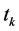 to
to , which is a kind of a regression-type estimator of
, which is a kind of a regression-type estimator of ![]()
based on the sample mean 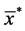 of the transformed auxiliary variable,
of the transformed auxiliary variable,![]() . Similarly, all the six estimators proposed by [1] could be easily identified as special cases of the proposed class of estimators. However, the advantage of the proposed class of estimators over the estimators proposed by [1] is that the proposed class of estimators generates a wider range of estimators of
. Similarly, all the six estimators proposed by [1] could be easily identified as special cases of the proposed class of estimators. However, the advantage of the proposed class of estimators over the estimators proposed by [1] is that the proposed class of estimators generates a wider range of estimators of![]() , especially those based on both the sample mean,
, especially those based on both the sample mean, ![]() and the transformed sample mean,
and the transformed sample mean,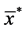 . For instance, choosing
. For instance, choosing  and
and ![]() in (10) reduces
in (10) reduces  to
to
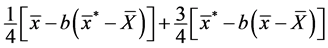 , which is a kind of a regression-type estimator of
, which is a kind of a regression-type estimator of ![]() based on both the sample mean
based on both the sample mean ![]() of the auxiliary variate,
of the auxiliary variate, 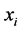 , and the sample mean
, and the sample mean 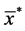 of the transformed auxiliary variable,
of the transformed auxiliary variable,![]() . Such combinations of estimators are not included among the estimators considered by [1] . Notice that here we assume that
. Such combinations of estimators are not included among the estimators considered by [1] . Notice that here we assume that ![]() is already known and therefore needs not to be estimated. Hence the expression
is already known and therefore needs not to be estimated. Hence the expression 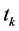 is not estimating
is not estimating ![]() in the real sense of it. To obtain the properties of the proposed class of estimators,
in the real sense of it. To obtain the properties of the proposed class of estimators, 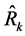 , we define the quantities:
, we define the quantities:
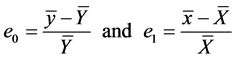 . (11)
. (11)
so that
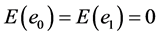 (12)
(12)
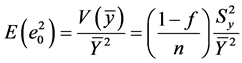 (13)
(13)
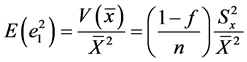 (14)
(14)
and
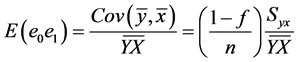 (15)
(15)
where 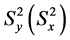 is the variance of
is the variance of 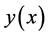 and
and 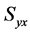 is the covariance of
is the covariance of ![]() and
and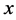 .
.
Consequently, rewriting the proposed class of estimators in (9) in terms of 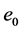 and
and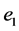 , and expanding up to first order approximations in expected values, we obtain:
, and expanding up to first order approximations in expected values, we obtain:
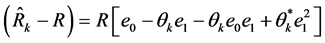 (16)
(16)
and
 (17)
(17)
so that if we take the expectations of (16) and (17), and use (12)-(15) to make the necessary substitutions, then the bias and mean squared error of the proposed class of estimators, 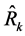 , are obtained, up to first order approximation, respectively as:
, are obtained, up to first order approximation, respectively as:
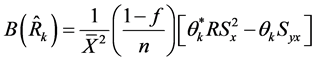 (18)
(18)
and
 (19)
(19)
where
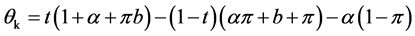 (20)
(20)
and
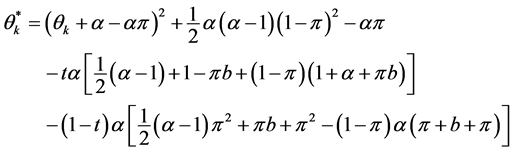 (21)
(21)
Using (18) to (21), the biases and mean squared errors of the special cases of the proposed class of estimators given in Table 1 are obtained as follows:
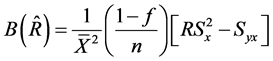 (22)
(22)
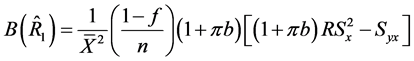 (23)
(23)
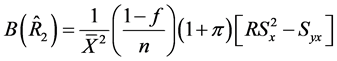 (24)
(24)
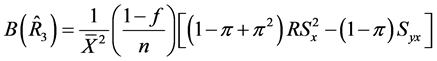 (25)
(25)
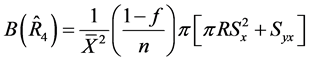 (26)
(26)
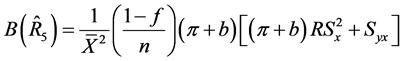 (27)
(27)
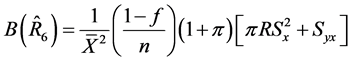 (28)
(28)
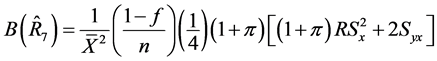 (29)
(29)
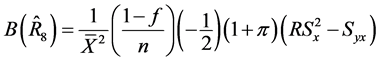 (30)
(30)
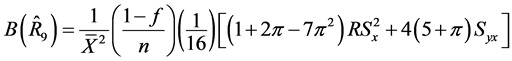 (31)
(31)
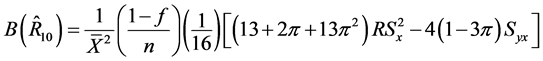 (32)
(32)
and,
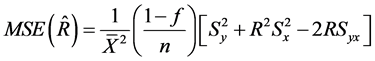 (33)
(33)
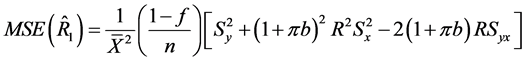 (34)
(34)
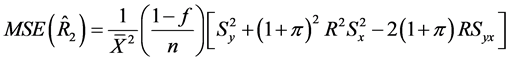 (35)
(35)
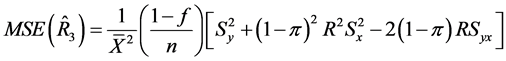 (36)
(36)
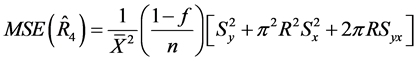 (37)
(37)
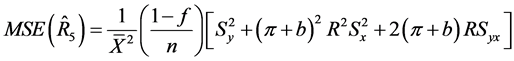 (38)
(38)
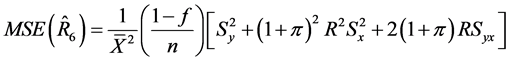 (39)
(39)
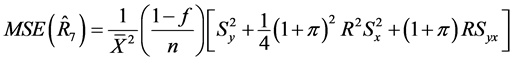 (40)
(40)
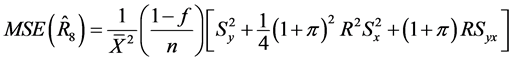 (41)
(41)
 (42)
(42)
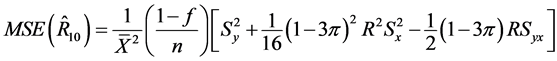 (43)
(43)
Notice that the estimators, 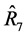 and
and 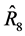 have equal mean squared errors.
have equal mean squared errors.
3. Efficiency Comparison
The efficiency comparison here is carried out on the basis of the estimators with smaller mean squared errors. Generally, it holds that any particular estimator, say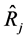 , in the proposed class of estimators,
, in the proposed class of estimators, 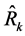 , would perform better than any given estimator,
, would perform better than any given estimator, 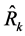 ,
,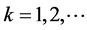 ;
;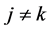 , in terms of having a smaller mean squared error if
, in terms of having a smaller mean squared error if
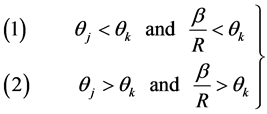 (44)
(44)
where 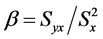 is the population regression coefficient of y on x;
is the population regression coefficient of y on x; ![]() and
and ![]() are obtained from (20).
are obtained from (20).
If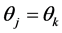 , then the estimator
, then the estimator 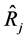 would be as efficient as the estimator
would be as efficient as the estimator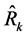 , since both estimators would have equal mean squared errors. Again, notice that
, since both estimators would have equal mean squared errors. Again, notice that ![]() for the customary ratio estimator,
for the customary ratio estimator, 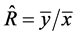 , which reduces (44) to
, which reduces (44) to
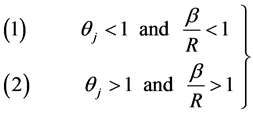 (45)
(45)
Consequently, the expression (45) is the efficiency condition for any particular estimator, say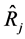 , in the proposed class of estimators,
, in the proposed class of estimators, 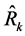 , to perform better than the usual ratio estimator,
, to perform better than the usual ratio estimator, 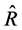 , in terms of having a smaller mean squared error.
, in terms of having a smaller mean squared error.
4. Numerical Illustration
Consider the data set given by [10], which can be summarized as follows:![]() ,
, ![]() ,
,  ,
,
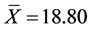 ,
, 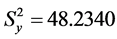 ,
, 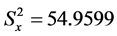 ,
, 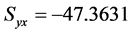
Table 2 shows 1) the percentage relative efficiency (PRE-1) of the proposed estimator, Table 2. Percentage relative efficiencies (pre) of proposed estimators. The percentage relative efficiencies (PRE-1) of Table 2 reveal that apart from the estimator, 5. Concluding Remarks In this paper, we have both generalized and extended the study carried out by [1]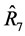 , over all other estimators given in table 1, and 2) the percentage relative efficiencies (PRE-2) of all other estimators in table 1 over the customary ratio estimator,
, over all other estimators given in table 1, and 2) the percentage relative efficiencies (PRE-2) of all other estimators in table 1 over the customary ratio estimator,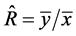 .
.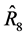 , the proposed regression-type estimator,
, the proposed regression-type estimator, 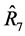 , based on both the sample means,
, based on both the sample means, ![]() and
and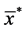 , is more efficient than the other estimators in table 1, including the customary ratio estimator,
, is more efficient than the other estimators in table 1, including the customary ratio estimator, 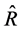 , in terms of having a smaller mean squared error. The table also shows that the estimator,
, in terms of having a smaller mean squared error. The table also shows that the estimator, 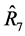 , has very large gains in efficiency over majority of the other estimators. Again, the percentage relative efficiencies (PRE-2) indicate that many of the proposed estimators have very large gains in efficiency over the customary ratio estimator,
, has very large gains in efficiency over majority of the other estimators. Again, the percentage relative efficiencies (PRE-2) indicate that many of the proposed estimators have very large gains in efficiency over the customary ratio estimator,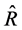 . However, the estimator,
. However, the estimator, 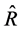 is more efficient than the ratio-type estimator,
is more efficient than the ratio-type estimator, 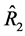 based on the sample mean,
based on the sample mean,![]() . This means that estimators in the proposed class are not uniformly better than the customary ratio estimator,
. This means that estimators in the proposed class are not uniformly better than the customary ratio estimator, . Theoretically, the efficiency condition (45) must be satisfied for any particular estimator in the proposed class to be more efficient than the customary ratio estimator,
. Theoretically, the efficiency condition (45) must be satisfied for any particular estimator in the proposed class to be more efficient than the customary ratio estimator,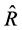 .
.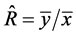 . Finally, it was remarked that the application of variable transformation of the auxiliary variable, x, in the present study, has effectively and maximally resulted in the use of auxiliary information for ratio estimation, without extra and real-time cost, often associated with the use of additional auxiliary information in estimating population ratio. This, of course, is the general motivation and advantage of the proposed class of estimators over other estimators of population ratio (R), under the simple random sampling scheme.
. Finally, it was remarked that the application of variable transformation of the auxiliary variable, x, in the present study, has effectively and maximally resulted in the use of auxiliary information for ratio estimation, without extra and real-time cost, often associated with the use of additional auxiliary information in estimating population ratio. This, of course, is the general motivation and advantage of the proposed class of estimators over other estimators of population ratio (R), under the simple random sampling scheme.
References
- Onyeka, A.C., Nlebedim, V.U. and Izunobi, C.H. (2013) Estimation of Population Ratio in Simple Random Sampling Using Variable Transformation. Global Journal of Science Frontier Research, 13, 57-65.
- Srivenkataramana, T. (1980) A Dual of Ratio Estimator in Sample Surveys. Biometrika, 67, 199-204. http://dx.doi.org/10.1093/biomet/67.1.199
- Singh, H.P. and Tailor, R. (2005) Estimation of Finite Population Mean Using Known Correlation Coefficient between Auxiliary Variables. Statistica, 65, 407-418.
- Tailor, R. and Sharma, B.K. (2009) A Modified Ratio-Cum-Product Estimator of Finite Population Mean Using Known Coefficient of Variation and Coefficient of Kurtosis. Statistics in Transition—New Series, 10, 15-24.
- Sharma, B. and Tailor, R. (2010) A New Ratio-Cum-Dual to Ratio Estimator of Finite Population Mean in Simple Random Sampling. Global Journal of Science Frontier Research, 10, 27-31.
- Onyeka, A.C. (2013) Dual to Ratio Estimators of Population Mean in Post-Stratified Sampling Using Known Value of Some Population Parameters. Global Journal of Science Frontier Research, 13, 13-23.
- Singh, M.P. (1965) On the Estimation of Ratio and Product of the Population Parameters. Sankhya, B27, 321-328.
- Srivastava, S.R., Khare, B.B. and Srivastaca, S.R. (1988) On Generalized Chain Estimator for Ratio and Product of Two Population Means Using Auxiliary Variables. Assam Statistical Review, 2, 21-29.
- Upadhyaya, L.N., Singh, G.N. and Singh, H.P. (2000) Use of Transformed Auxiliary Variable in the Estimation of Population Ratio in Sample Survey. Statistics in Transition, 4, 1019-1027.
- Pandey, B.N. and Dubey, V. (1988) Modified Product Estimator Using Coefficient of Variation of Auxiliary Variate. Assam Statistical Review, 2, 64-66.


