Open Journal of Geology
Vol.06 No.11(2016), Article ID:72295,12 pages
10.4236/ojg.2016.611104
Impact of Soil Type Used in Tunneling on Land Subsidence and Mobility Effective Time under Different Earthquake Records
Arash Rostami1, Alireza Firoozfar2, Behnam Adhami1, Nima Asghari3
1Department of Civil Engineering, Islamic Azad University Central Tehran Branch, Tehran, Iran
2Department of Civil Engineering, University of Zanjan, Zanjan, Iran
3Department of Civil Engineering, Noshirvani University of Technology, Babol, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 23, 2016; Accepted: November 25, 2016; Published: November 28, 2016
ABSTRACT
During recent decades, tunnels construction in urban environments has been recognized as a useful factor in improving transportation situation in cities. Construction of underground structures like tunnels has a direct impact on the above-ground structures. The most important impacts are soil crust movement of the structure movement), acceleration change of the earthquake on structures, and land subsidence. The present research aims at seismic evaluation of the effect of soil type in land subsidence and effective mobility time in tunneling projects. For this purpose, two different soil types are chosen to model and assess factors using numerical methods. The outcome of this research concludes that tunneling changes in the dominant frequency record if these changes reach to the extent that structure frequency equals to record frequency, resonance phenomenon happens.
Keywords:
Soil Type, Dominant Frequency, Movement Duration, Soil Subsidence

1. Introduction
The increasing rate of population growth in big cities and as a result high volume of traffic, make authorities build tunnels by engineering help engineers. Tunneling in each depth of soil led to some variations in land surface. This issue is significantly important in urban tunneling especially when they pass under residual districts. Therefore, awareness from tunnel behavior and digging resulted effects is necessities of preventing from structures damages. Another important effect which is effective on ground surface subsidence is dominant frequency of the imposed record on soil. In other words, dynamic forces influence differently on earth by various frequencies. Dowding, C.H., Rozen (1978) [1] assessed behaviors of 71 tunnels in California, Alaska, and Japan. Results of studies showed that tunnels damage in soft soil or rocky soils is higher than the other soils. Vakabashi (1985), Tabatabai Far (2007) [2] evaluated seismic behavior of structures by examining soil-structure interaction and stated that taking into account the soil-structure interaction reduces the natural frequency of the system, increases mortality, increases lateral displacement, and reduces the base shear of structures. St-John, and Zahrah, (1987) [3] by studying tunnel-structure interaction stated that when dominant frequency of tunnel soil and the examined structure are close to each other, it will make double resonance and more damages. Cilingir & Madabhushi, (2011) [4] examined effects of earthquake forces with different frequencies and amplitudes on circular and square tunnels and stated that by increasing in Fourier spectrum frequency increase and reduced acceleration in high frequency time, Fourier spectrum and acceleration increase. Abuhajer et al. (2011) [5] investigated effects of digging tunnel on earthquake acceleration by different records modellings by modeling square tunnel in sand soil. Rostami et al. (2016) [6] investigated the effect of tunnels on slopes and found this interaction effect on ground response. On other effort Rostami et al. (2016) [7] worked on effect of tunnel maintenances on ground response and conducted that the tunnel maintenance had direct effect on ground response. Musivand and Asgariziarati (2014) [8] examined earth surficial slope and frequency on earth surface movement using Plaxis software. Besides determining dominant frequencies that make the maximum horizontal and vertical movements, state that earth surface slope doesn’t influence on dominant frequency. Musivand et al. (2014) [9] examined effect of earth surface slope effect and frequency on resulted earth surface movements by digging deep tunnels under harmonic dynamic loads and stated that increase in earth surface slope increases vertical subsidence of top of tunnel and also change in earth surface slop doesn’t influence on dominant frequency. Rostami et al. (2016) [10] investigated effect of tunnel gate shapes with similar cross section on inserted forces and conducted that the rectangular tunnels had more effect on surface responses. Rostami et al. (2016) [11] evaluated seismic behavior and earth’s surface acceleration, by interaction of tunnels with different shapes and different types of soils. Also Alielahi et al. [12] (2015) worked on seismic ground amplification by unlined tunnels and concluded that the effect of the tunnel on the seismic ground surface response is gradually decreased or becomes insignificant with increasing the buried depth of the tunnel. Several researchers (e.g. Iwan et al., 2000 [13] ; Krawinkler et al., 2003 [14] ; Galal and Naimi, 2008 [15] ; El Ganainy and El Naggar, 2009 [16] ; Tabatabaiefar and Massumi, 2010 [17] ; Tavakoli et al., 2011 [18] ) studied structural behaviour of un-braced structures subjected to earthquake under the influence of soil-structure interaction.
2. Methodology
2.1. Materials
In this research, two soil types with recorded specification in Table 1, Table 2, are used. The table shows that shear wave velocity of soil (2) is less than shear wave velocity of soil type (2), it can be claimed that soil (2) is harder than soil (1). Each soil type has one layer and no underground water. The mentioned soil is homogenous with elastic-per- fectly plastic behavior with Mohr-Coulomb regulation. Having 5 parameters of elastic module (E), internal friction angle φ, dilation angle ψ, cohesion (C), Poison coefficient of soil we can write behavioral model equations. Using the mentioned parameters and soil specific weight, we can calculate shear module (G) and shear wave velocity VS.2.2, maintaining the Integrity of the Specifications.
2.1. Modelling and Analysis
Soil layer and tunnel are modeled in Abaqus. The recorded soil types in Table 1 are modeled in the mentioned software then tunnels with different shapes, cross sections, and placement depth will be dug. Concrete coverage of tunnel and structure foundation was modeled by elastic behavior of flexural element and materials parameters are attributed to them. To define mutual interfaces of elements, interface element 1 was used. Meshing in the second step in software, then lateral forces as harmonic sine and earthquake real record analyze model so needed responses such as earthquake acceleration in soil level will be extracted.
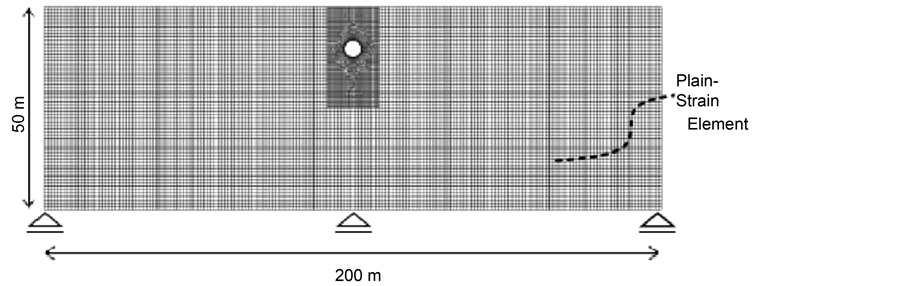
Figure 1 shows the general scheme of the developed model. In this figure, d is tunnel diameter and h stands for placement depth (height), (the distance between the tunnel center and the earth surface) and b represents the width of the structure foundation. The dug tunnels in model are as the following tables. In Table 3, Table 4 tunnel shape
Table 1. Soil specifications (Afifpour et al., 2011) [19] .
Table 2. Tunnel coverage specifications (Maleki et al., 2011).
Figure 1. Model general scheme.
Table 3. Specification of circular tunnel with different diameters.
Table 4. Tunnel specifications with different heights.
and its depth is constant and tunnel diameter is varied, the ration of d/h will be considered as variable. In Table 5, tunnel shape and diameter will be constant and placement height is varied; therefore, d/h is variable in this table. In Table 6, tunnel shape is varied and other variables are constant. The purpose to say tunnel placement height is distance of tunnel center from the earth surface.
To define boundary conditions, constant and energy absorber boundaries are used. In constant boundary, roller support is considered for vertical lines, joint support is considered for horizontal line of soil and horizontal line above soil is without any support. In this way, soil has movement in vertical direction and doesn’t have any movement in horizontal direction. While inserting dynamic loads, waves reflect on model boundaries for turbulence. To prevent the intensive reflections, energy absorber boundaries in low part, left and right sides are used. Analysis software meshes model to 6 or 15 dots triangles that are called meshing. In Abaqus, there are very big, big, medium, small, and very small meshing. Meshing depends on the importance of use. By selecting very big meshing, results of analyses won’t be so precise and very small meshing selection increases analysis time.
Effective movement time can be calculated by three methods. The first method is called Uniform Method. Time collection with absolute acceleration higher than 0.05 g was considered as effective movement time. Second method is called Bracheted Method. In this method, effective time movement is between the first value time and the last absolute acceleration value that is higher than 0.05 g. the Third method is called significant (energy method) knowing effective movement time between 5% and 95% of earthquake energy. Among the mentioned methods, energy method gives more precise response to effective movement time. Interface resistance coefficient value can be used for various types of structure-soil interactions by scientific breakthroughs, in impossibility of access to these factors, value of 0.7 can be considered. The most important dynamic analysis parameters are dynamic analysis time, time intervals, and equations solutions method. In this research, a time of 30 s as analysis time, with 0.03 time interval, was considered. In addition, Newmark design was used to solve equations as the numerical method (Figures 2-7).
3. Results and Discussion
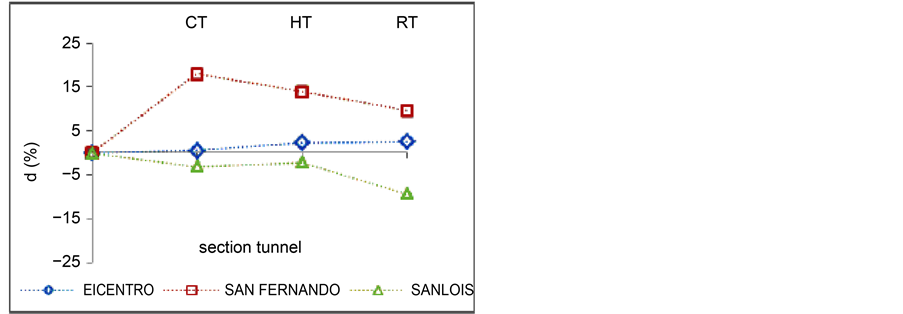
According to Figure 8 showing changes in record dominant frequency made by digging tunnel in soil (1) than without tunnel, it is indicated that the most frequency reduction is related to San Luis earthquake which was similar for all three types of tunnels. Generally, it can be stated that frequency changes are similar for all three tunnels for each record. In Figure 8 and Figure 9, f was change percentage of dominant frequency and FA was change percentage of Fourier spectrum amplitude which was calculated by the following relations. FT is record dominant frequency in the state with the
Table 5. Tunnel specifications with different shapes.
Table 6. Specifications of harmonic sine record.
Figure 2. Sine record with 2 Hz frequency.
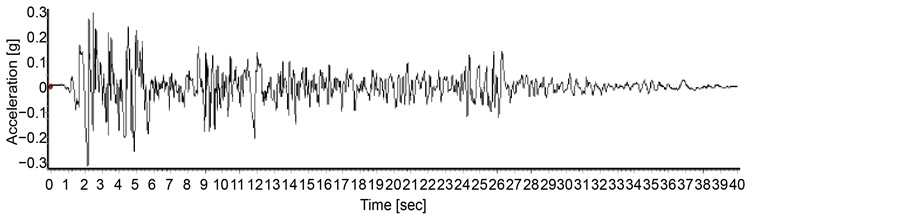
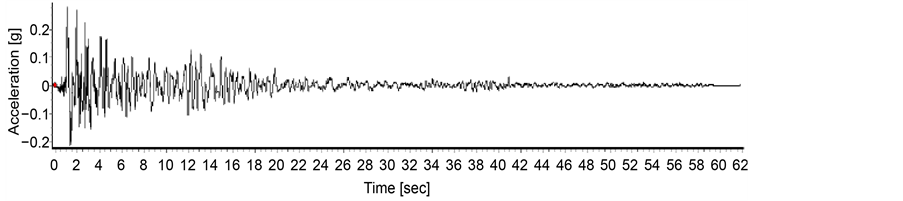
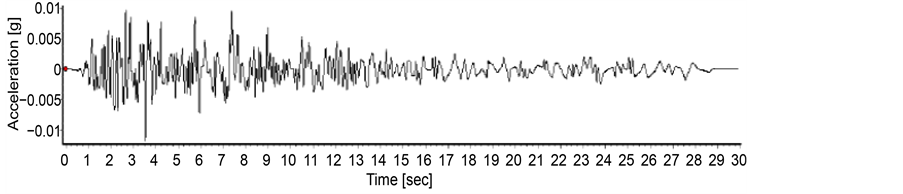
Figure 3. El Centro earthquake record.
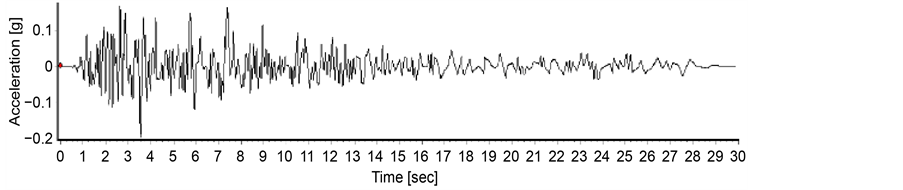
Figure 4. San Fernando earthquake record.
Figure 5. San Luis earthquake record.
Figure 6. Record compared to 0.2 g of San Fernando earthquake.
Figure 7. Record compared to 0.2 g of San Fernando earthquake.
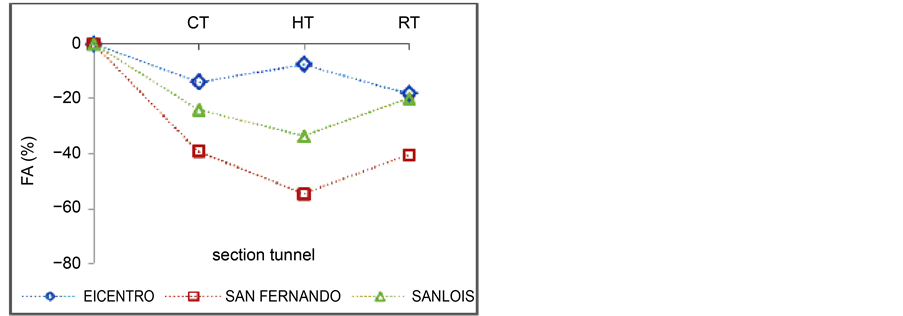
Figure 8. Change percentage of record dominant frequency in soil 1.
Figure 9. Change percentage of maximum Fourier amplitude in soil 1.
presence of tunnel and FWT is in the case of without tunnel. FAT is the maximum Fourier spectrum amplitude in the states with tunnel and FAWT is the maximum Fourier spectrum amplitude in states without tunnel. The positive part of vertical vector shows increase percentage and its negative part shows reduction percentage. The parameters of the dynamic analysis, dynamic analysis time, step time, and method are solved. In this study, time and time step of 30 seconds, 0.03 seconds is considered, as well as numerical methods are used for solving equations of Newmark scheme.
Figure 8 shows the percentage change based on the dominant frequency record by tunneling under the soil 1 to show off the tunnel is clear that the greatest reduction in frequency related to the earthquake for all three types of Saint-Louis Generally speak- ing, it to the tunnel is identical The frequency changes in all three tunnels for the same record. In Figure 8 and Figure 9, f, the percentage change in the dominant frequency and FA percentage change in the maximum range Fourier spectrum that are calculated from the following relations. FT, dominant frequency record in the tunnel and FWT, dominant frequency record in the tunnel is no FAT, maximum amplitude Fourier spectrum record in the tunnel and FAWT, maximum amplitude Fourier spectrum is a record in tunnel mode without positive the vertical axis shows the percentage and the reduction of its negative.
Before you begin to format your paper, first write and save the content as a separate text file. Keep your text and graphic files separate until after the text has been formatted and styled. Do not use hard tabs, and limit use of hard returns to only one return at the end of a paragraph. Do not add any kind of pagination anywhere in the paper. Do not number text heads―the template will do that for you.
Finally, complete content and organizational editing before formatting. Please take note of the following items when proofreading spelling and grammar:
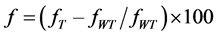

F: changes percentage of record dominant frequency.
FA: changes percentage of maximum Fourier spectrum amplitude.
Figure 10 shows change percentage of record dominant frequency by digging tunnel in soil 2 than without tunnel state. As it is indicated, frequency changes in all three tunnels are very negligible in each record. Figure 11 shows change percentage of maxi- mum Fourier record amplitude by digging tunnel in soil 2 than state without tunnel. As
Figure 10. Change percentage of record dominant frequency in soil 2.
Figure 11. Change percentage of maximum Fourier amplitude in soil 2.
it is shown, the maximum Fourier amplitude is reduced in all records and the most reduction is related to San Luis earthquakes. Figure 10 and Figure 11, f is change percentage of dominant frequency and FA is change percentage of maximum amplitude of Fourier spectrum which is calculated by the mentioned relations. The positive part of vertical vector shows increase percentage and its negative part shows reduction percentage.
3.1. Comparison Fourier Spectrum by Digging Tunnel with Various Cross Sections in Soil 1 and 2 under Earthquake Records
Fourier spectrum will change for soil types 1 and 2 in tunnels with different cross sections and various records. In addition, Fourier spectrum change in soil type 1 is for softness of soil 1 and soil type 2. Fourier spectrum change was confirmed by Cilingir, U., & Madabhushi (2011). Table 7 shows change percentage of record dominant frequency in state with tunnel than state without tunnel under earthquakes under various records of earthquakes in soil type 1 and 2. It can be concluded from the mentioned table that frequency change percentage is mostly more in soil type 1 than soil type 2. In soil type 2, most record dominant frequency in soil 1 is relatively more than soil 2. In soil 2, frequency of most records won’t change by digging tunnel for soil stiffness. Table 8 shows change percentage of record maximum Fourier spectrum amplitude in
Table 7. Change percentage of record dominant frequency by digging tunnel under various earthquake records in soil types 1 and 2.
Table 8. Change percentage of record dominant frequency by digging tunnel under various earthquake records in soil types 1 and 2.
state with tunnel than state of without tunnel under various earthquakes records in soil 1 and 2. It can be concluded from the mentioned table that Fourier spectrum amplitude decrease in both soil types so that change percentage of maximum Fourier spectrum amplitude in soil type 1 is relatively more than soil type 2.
3.2. Effective Movement Duration of Earthquake Record
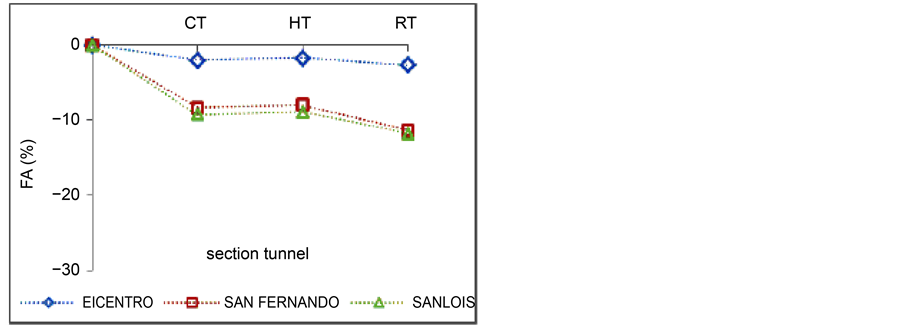
Each record has effective movement duration (time). Effective movement duration is defined by different methods which the most important and precise is energy method. In this method, duration of releasing 5% to 95% of energy is measured. It is tried in this research to examine effects of digging tunnel in both types of soil and compare the results with state without tunnel. Figure 12, Figure 13 show change percentage of effective record movement duration and as it is indicated, record type, soil type, and tunnel type have direct effect on effective movement duration. In soil type (1), effective move- ment duration in San Fernando and El Centro earthquakes increased and reduced in San Luis earthquake. But in soil type (2), increase in effective movement duration is seen in all records.
Figure 12. Change percentage of effective movement duration in soil 1.
Figure 13. Change percentage of effective movement duration of record in soil type 2.
4. Conclusions
Real earthquake records including El Centro, San Fernando, and San Luis imposed on soil surface in states with and without tunnels (including circular, horseshoe, and rectangular tunnels with similar cross section) were considered. Obtained results of modelling are as following.
One application of record Fourier spectrum is for determining dominant frequency limitation. The real imposed records to the soil floor are changed by digging different cross section tunnels such as frequency content, maximum acceleration, change in occurrence of maximum acceleration and so on so that change in dominant frequency in soil type (1) is relatively more in soil type (2). In both soil types, the maximum Fourier spectrum of dominant frequency reduces so that change percentage of maximum Fourier spectrum amplitude in soil (1) is relatively more than soil type (2). This is for more stiffness of soil type (2) than type (1). It is noticeable that digging tunnel changes record dominant frequency. If these changes are to the extent that structure and record frequencies are relatively similar, resonance happens and may impose great damages. Another parameters of real earthquake record parameters made by digging tunnel are effective movement duration. Record type and tunnel type have direct effect on effective placement duration. In soil type (1), effective movement duration in San Fernando and El Centro increased and in San Luis reduced, but in soil type (2), effective movement duration increased in all records.
Cite this paper
Rostami, A., Firoozfar, A., Adhami, B. and Asghari, N. (2016) Impact of Soil Type Used in Tunneling on Land Subsidence and Mobility Effective Time under Different Earthquake Records. Open Journal of Geology, 6, 1469-1480. http://dx.doi.org/10.4236/ojg.2016.611104
References
- 1. Dowding, C.H. and Rozen, A. (1978) Damage to Rock Tunnels from Earthquake Shaking. Journal of the Geotechnical Engineering Division, 104, 175-191.
- 2. Massumi, A. and Tabatabaiefar, H.R. (2007) Effects of Soil-Structure Interaction on Seismic Behavior of Ductile Reinforced Concrete Moment Resisting Frames. World Housing Congress on Affordable Quality Housing (WHC2007): Challenges and Issues in the Provision of Shelter for All, China, January 2007.
- 3. St-John, C.M. and Zahrah, T.F. (1987) Asiesmic Design of Underground Sructures. Tunneling and Underground Space Technology, 2, 165-197.
https://doi.org/10.1016/0886-7798(87)90011-3 - 4. Cilingir, U. and Madabhushi, S.G. (2011) A Model Study on the Effects of Input Motion on the Seismic Behaviour of Tunnels. Soil Dynamics and Earthquake Engineering, 31, 452-462.
https://doi.org/10.1016/j.soildyn.2010.10.004 - 5. Abuhajar, O., El Naggar, H. and Newson, T. (2011) Effects of Underground Structures on Amplification of Seismic Motion for Sand with Varying Density. Pan-Am CGS Geotechnical Conference, Toronto, 6 October 2011.
- 6. Rostami, A., Alielahi, H., Zare, M. and Haghighi, K. (2016) Frequency and Surface Slope’s Effects on the Surface Displacement by Drilling Shallow and Deep Tunnels under Dynamic Loads. Open Journal of Marine Science, 6, 353-370.
https://doi.org/10.4236/ojms.2016.63030 - 7. Rostami, A., Kamali-Dehkordi, P., Askari-Ziarati, M, Jahani, S. and Lotfi, K. (2016) The Types of Tunnel Maintenancein Umbrella Arch Method. Open Journal of Civil Engineering, 6, 156-162. http://dx.doi.org/10.4236/ojce.2016.62014
- 8. Musivand, M. and Asgari Ziyarati, M. (2014) Effect of Earth Surface Slope and Frequency on Earth Surface Movements Resulted by Digging Deep Tunnels under Harmonic Dynamic Loads. The 1st Architectural Conference, Urban Civil and Environment, Hamedan, 1 March 2014.
- 9. Musivand, M. and ASgari Ziyarati, M. (2014) Effects of Frequency and Earth Slope on Earth Surface Movement by Digging Low-Deep Tunnels under Dynamic Loads. The 1st Constructing Conference of Civil Projects Evaluation and Construction, Gorgan, 1 May 2014.
- 10. Rostami, A., Asghari, N., Askari Ziarati, M., Jahani, S. and Shahi, B. (2016) Investigating Effect of Tunnel Gate Shapes with Similar Cross Section on Inserted Forces on Its Coverage and Soil Surface Settlement. Open Journal of Civil Engineering, 6, 358-369.
https://doi.org/10.4236/ojce.2016.63030 - 11. Rostami, A., Askari-Ziarati, M., Jahani, S. and Shahi, B. (2016) Evaluation of Seismic Behavior and Earth’s Surface Acceleration, by Interaction of Tunnels with Different Shapes and Different Types of Soils. Open Journal of Civil Engineering, 6, 242-253.
https://doi.org/10.4236/ojce.2016.62022 - 12. Alielahi, H., Kamalian, M. and Adampira, M. (2015) Seismic Ground Amplification by Unlined Tunnels Subjected to Vertically Propagating SV and P Waves Using BEM. Soil Dynamics and Earthquake Engineering, 71, 63-79.
https://doi.org/10.1016/j.soildyn.2015.01.007 - 13. Iwan, W.D., Huang, C.T. and Guyader, A.C. (2000) Important Features of the Response of Inelastic Structures to Near-Field Ground Motion. Proceedings of the 12th World Conference on Earthquake Engineering, New Zealand Society for Earthquake Engineering, New Zealand, Paper No. 1740.
- 14. Krawinkler, H., Medina, R. and Alavi, B. (2003) Seismic Drift and Ductility Demands and Their Dependence on Ground Motions. Engineering Structures, 25, 637-653.
https://doi.org/10.1016/S0141-0296(02)00174-8 - 15. Galal, K. and Naimi, M. (2008) Effect of Conditions on the Response of Reinforced Concrete Tall Structures to Near Fault Earthquakes. The Structural Design of Tall and Special Buildings, 17, 541-562.
https://doi.org/10.1002/tal.365 - 16. El Ganainy, H. and El Naggar, M.H. (2009) Seismic Performance of Three-Dimensional Frame Structures with Underground Stories. Soil Dynamics and Earthquake Engineering, 29, 1249-1261.
https://doi.org/10.1016/j.soildyn.2009.02.003 - 17. Tabatabaiefar, H.R. and Massumi, A. (2010) A Simplified Method to Determine Seismic Responses of Reinforced Concrete Moment Resisting Building Frames under Influence of Soil-Structure Interaction. Soil Dynamics and Earthquake Engineering, 30, 1259-1267.
https://doi.org/10.1016/j.soildyn.2010.05.008 - 18. Tavakoli, H.R., Naeej, M. and Salari, A. (2011) Response of RC Structures Subjected to Near Fault and Far Fault Earthquake Motions Considering Soil-Structure Interaction. International Journal of Civil and Structural Engineering, 1, 881-896.
- 19. Afifipour, M., Sharifzadeh, M., Shahriar, K. and Jamshidi, H. (2011) Interaction of Twin Tunnels and Shallow Foundation at Zand Underpass, Shiraz Metro, Iran. Tunnelling and Underground Space Technology, 26, 356-363.
https://doi.org/10.1016/j.tust.2010.11.006