Open Journal of Discrete Mathematics
Vol.06 No.04(2016), Article ID:70748,18 pages
10.4236/ojdm.2016.64024
Excluded Minority of P8 for GF(4)-Representability
Seungho Ahn, Boongbi Han
Department of Mathematics, Chonnam National University, Gwangju, South Korea

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 3, 2015; Accepted: September 18, 2016; Published: September 21, 2016
ABSTRACT
One of the mainly interesting things of matroid theory is the representability of a matroid. Finding the set of all excluded minors for the representability is the solution of the representability. In 2000, Geelen, Gerards and Kapoor proved that 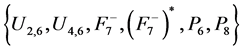 is the complete set of GF(4)-representability. In this paper, we show that
is the complete set of GF(4)-representability. In this paper, we show that  is an excluded minor for GF(4)-representability.
is an excluded minor for GF(4)-representability.
Keywords:
Excluded Minor

1. Introduction
Matroid theory dates from the 1930’s when Whitney first used the term matroid in his basic paper [1] . Matroid theory is a common generalization of linear independence of graphs and matrices. One of the mainly interesting things of matroid theory is the representability of a matroid. One problem of representability is to find the fields over which the given matroid is representable. The other problem is to find the excluded minors for which the matroid is representable over the given field. It was found the complete set of excluded minors for two or three element fields [2] - [5] . In 1984, Kahn and Seymour conjectured that 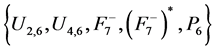 is the complete set of ex- cluded minors for GF(4)-representability. Oxley showed that the conjecture is wrong by showing
is the complete set of ex- cluded minors for GF(4)-representability. Oxley showed that the conjecture is wrong by showing  is also excluded minor for GF(4)-representability in his brief note [6] . Geelen, Gerarads and Kapoor proved that it is enough to add
is also excluded minor for GF(4)-representability in his brief note [6] . Geelen, Gerarads and Kapoor proved that it is enough to add 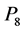 to the list of Kahn and Seymour [7] . It is not an easy problem to find the excluded minors for GF(q)- representability when q is more than 4. Instead, we have the conjecture by Rota that the number of excluded minors are finite for any prime powers q [8] . In this paper, we study the properties of minor and show that
to the list of Kahn and Seymour [7] . It is not an easy problem to find the excluded minors for GF(q)- representability when q is more than 4. Instead, we have the conjecture by Rota that the number of excluded minors are finite for any prime powers q [8] . In this paper, we study the properties of minor and show that 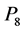 is excluded minor for GF(4)- representability deliberately.
is excluded minor for GF(4)- representability deliberately.
2. Preliminaries
2.1. Matroid
Matroid theory has exactly the same relationship to linear algebra as does point set topology to the theory of real numbers. That is, point set topology postulate the pro- perties of the open sets of real line and matroid axiomatize the character of the in- dependent set in vector space:
Definition 2.1. A matroid M is a finite set E and a collection 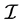 of subsets of E satisfying the following three conditions:
of subsets of E satisfying the following three conditions:
(I1)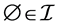 .
.
(I2) If 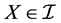 and
and 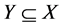 then
then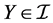 .
.
(I3) If X, Y are in 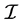 and
and , then there exists
, then there exists 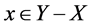 such that
such that 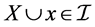 .
.
By the definition, for a finite vector space V and for the collection of linearly independent subsets 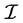 of vectors of V,
of vectors of V, 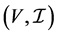 is a matroid. If
is a matroid. If 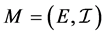 is a matroid, M is called a matroid on E. Also E which is denoted by
is a matroid, M is called a matroid on E. Also E which is denoted by ![]() is called ground set of M and
is called ground set of M and ![]() is called the set of independent set in M. A subset of E that is not in
is called the set of independent set in M. A subset of E that is not in ![]() is called dependent set. On the other point of view, matroid can be defined by abstraction of the properties of the cycles of a graph. Let G be a graph and let
is called dependent set. On the other point of view, matroid can be defined by abstraction of the properties of the cycles of a graph. Let G be a graph and let ![]() be the set of all edges of G. Also let
be the set of all edges of G. Also let ![]() be the set of all cycles in G. Then
be the set of all cycles in G. Then ![]() has the following properties:
has the following properties:
(C1)![]() .
.
(C2) If ![]() and
and ![]() are in
are in ![]() and
and![]() , then
, then![]() .
.
(C3) If ![]() and
and ![]() are distinct members of
are distinct members of ![]() and
and![]() , then there is member
, then there is member ![]() of
of ![]() such that
such that![]() .
.
Now, let ![]() be a subset of the power set
be a subset of the power set ![]() of a finite set E. If
of a finite set E. If ![]() satisfies the conditions (C1), (C2) and (C3), then
satisfies the conditions (C1), (C2) and (C3), then ![]() is called the set of circuits of a matroid on E. Let
is called the set of circuits of a matroid on E. Let ![]() be the set of circuits of a matroid M. Then, the set
be the set of circuits of a matroid M. Then, the set ![]() of all subsets of E which contain no member of
of all subsets of E which contain no member of ![]() satisfies the independent conditions (I1), (I2) and (I3). Also for a matroid
satisfies the independent conditions (I1), (I2) and (I3). Also for a matroid![]() , the set
, the set ![]() of all minimal dependent set M satisfies the three circuits conditions. Thus, the matroid defined by circuits is the same as the one defined by independent sets. We need two other definitions of a matroid.
of all minimal dependent set M satisfies the three circuits conditions. Thus, the matroid defined by circuits is the same as the one defined by independent sets. We need two other definitions of a matroid.
Definition 2.2. Let E be a finite set and r be a function from ![]() to the set of non- negative integers and satisfies the following conditions:
to the set of non- negative integers and satisfies the following conditions:
(R1) If![]() , then
, then![]() .
.
(R2)![]() , then
, then![]() .
.
(R3) If X and Y are subsets of E, then![]() . Then, r is called the rank function of a matroid M on E. Let M be the matroid
. Then, r is called the rank function of a matroid M on E. Let M be the matroid ![]() and suppose that
and suppose that![]() . Let
. Let ![]() be
be![]() . Then, it is easy to see that the pair
. Then, it is easy to see that the pair ![]() is a matroid. We call this matroid the restriction of M to X or the deletion of
is a matroid. We call this matroid the restriction of M to X or the deletion of ![]() from M. It is denoted by
from M. It is denoted by ![]() or
or![]() . We define the rank
. We define the rank ![]() of X to be the size of a maximal independent set of
of X to be the size of a maximal independent set of![]() . This function which is called the rank function of M satisfies the conditions (R1), (R2) and (R3). This function is denoted by
. This function which is called the rank function of M satisfies the conditions (R1), (R2) and (R3). This function is denoted by ![]() and
and ![]() will be denoted by
will be denoted by![]() . On the other hand, if r is a rank function of a matroid M, the set
. On the other hand, if r is a rank function of a matroid M, the set ![]() is the set of in- dependent set of M. Thus, the definition of a matroid by a rank function is equivalent to the definition by independent sets. One of the definitions of matroid is the one by closure operator. Throughout this thesis, by E means a finite set.
is the set of in- dependent set of M. Thus, the definition of a matroid by a rank function is equivalent to the definition by independent sets. One of the definitions of matroid is the one by closure operator. Throughout this thesis, by E means a finite set.
Definition 2.3. Let cl be a function from ![]() to
to ![]() satisfying the following;
satisfying the following;
(CL1) If![]() , then
, then![]() .
.
(CL2) If![]() , then
, then![]() .
.
(CL3) If![]() , then
, then![]() .
.
(CL4) If![]() ,
, ![]() , and
, and![]() , then
, then![]() .
.
Then cl is called the closure operator of a matroid M on E. Let M be a matroid on E with the rank function r. Define cl to be the function from ![]() to
to ![]() by
by
![]() for all
for all![]() . Then, we can see that cl satisfies (CL1)-(CL4). On the other hand, if cl is the closure operator of a matroid M on E, then
. Then, we can see that cl satisfies (CL1)-(CL4). On the other hand, if cl is the closure operator of a matroid M on E, then ![]() satisfies the independent axioms and
satisfies the independent axioms and ![]() is the matroid having closure operator cl. Thus, the four definitions of matroid defined by the above are equivalent. We can see that there are a lot of equivalent definition of matroid. We have to introduce one more definition of matroid. For a matroid M, the maximal independent set in M is called a basis or base of M. It is easy to see that every basis element has the same cardinal number. Let
is the matroid having closure operator cl. Thus, the four definitions of matroid defined by the above are equivalent. We can see that there are a lot of equivalent definition of matroid. We have to introduce one more definition of matroid. For a matroid M, the maximal independent set in M is called a basis or base of M. It is easy to see that every basis element has the same cardinal number. Let ![]() be the set of all base element of M. Then,
be the set of all base element of M. Then, ![]() has the properties;
has the properties;
(B1) ![]() is non-empty.
is non-empty.
(B2) If ![]() and
and ![]() are in
are in ![]() and
and ![]() then there is
then there is ![]() such that
such that![]() .
.
Conversely, let ![]() be a collection of subsets of E satisfying the axioms (B1) and (B2). And let
be a collection of subsets of E satisfying the axioms (B1) and (B2). And let![]() . Then
. Then ![]() is a matroid having
is a matroid having ![]() as its collection of bases. If M is a matroid and
as its collection of bases. If M is a matroid and![]() , then we call
, then we call ![]() the closure or span of X in M, and we write this as
the closure or span of X in M, and we write this as![]() . If
. If![]() , then X is called a flat or a closed set of M. A hyperplane of M is a flat of rank
, then X is called a flat or a closed set of M. A hyperplane of M is a flat of rank![]() . A subset X of
. A subset X of ![]() is a spanning set of M if
is a spanning set of M if![]() . Let M be a matroid and
. Let M be a matroid and ![]() be
be![]() . Then,
. Then, ![]() satisfies the following axiom which is equivalent to (B2):
satisfies the following axiom which is equivalent to (B2):
(B2)* If ![]() and
and ![]() are in
are in ![]() and
and![]() , then there is an element
, then there is an element ![]() such that
such that![]() . The matroid
. The matroid ![]() having the set of all basis element B*(M) is called the dual of M. Thus
having the set of all basis element B*(M) is called the dual of M. Thus ![]() and
and![]() . Also
. Also![]() . The bases of
. The bases of ![]() are called cobases of M. Similarly, the circuits, hyperplanes, independent sets and spanning sets of
are called cobases of M. Similarly, the circuits, hyperplanes, independent sets and spanning sets of ![]() are called cocircuits, cohyperplanes, coindependent sets, and cospanning sets of M. The next result gives some elementary relationships between these sets.
are called cocircuits, cohyperplanes, coindependent sets, and cospanning sets of M. The next result gives some elementary relationships between these sets.
Proposition 2.4. Let M be a matroid on a set E and suppose![]() . Then
. Then
1) X is independent if and only if ![]() is cospanning.
is cospanning.
2) X is spanning if and only if ![]() is coindependent.
is coindependent.
3) X is a hyperplane if and only if ![]() is cocircuit.
is cocircuit.
4) X is a circuit if and only if ![]() is a cohyperplane.
is a cohyperplane.
Proof. 1) Let X be an independent set in M. Then, ![]() for some basis element B of M. Thus
for some basis element B of M. Thus ![]() and
and![]() , where
, where ![]() is the clo- sure in
is the clo- sure in![]() . If
. If ![]() is cospanning, then
is cospanning, then ![]() for some basis element
for some basis element ![]() of
of![]() . It means that
. It means that ![]() and X is independent set. 2) is deduced by applying 1) to
and X is independent set. 2) is deduced by applying 1) to![]() . 3) is obtained by the following equivalent statements; a) X is a hyperplane of M. b) X is a non-spanning set of M but
. 3) is obtained by the following equivalent statements; a) X is a hyperplane of M. b) X is a non-spanning set of M but ![]() is spanning for all
is spanning for all![]() . c)
. c) ![]() is dependent in
is dependent in ![]() but
but ![]() is independent in
is independent in ![]() for all
for all![]() . d)
. d) ![]() is a cocircuit of M. 4) is the one obtained by applying 3) to
is a cocircuit of M. 4) is the one obtained by applying 3) to![]() .
.
□
Let’s remind of the finite fields. If F is a finite field, then F has exactly pk-elements for some prime p and some positive integer k. Indeed, for all such p and k, there is a unique field ![]() having pk-elements. This field is called the Galois field of order pk. When
having pk-elements. This field is called the Galois field of order pk. When![]() ,
, ![]() coincides with
coincides with![]() , the ring of integers modulo p. When
, the ring of integers modulo p. When![]() ,
, ![]() can be constructed as follows. Let
can be constructed as follows. Let ![]() be a polynomial of degree k with coefficients in
be a polynomial of degree k with coefficients in ![]() and suppose that the polynomial is irreducible. Consider the set S of all polynomials in
and suppose that the polynomial is irreducible. Consider the set S of all polynomials in ![]() that have degree at most
that have degree at most ![]() and have coefficients in
and have coefficients in![]() . There are exactly p choices for each of the k-coefficient of a member of S. Hence,
. There are exactly p choices for each of the k-coefficient of a member of S. Hence,![]() . If we take p = 2 and k = 2 we get the field GF(4). Moreover, under addition and multiplication, both of which are performed modulo
. If we take p = 2 and k = 2 we get the field GF(4). Moreover, under addition and multiplication, both of which are performed modulo![]() , S forms a field namely
, S forms a field namely![]() . In case of
. In case of![]() , we can take the irreducible polynomal to
, we can take the irreducible polynomal to ![]() .
.
Let A be a matrix over a field F. Then, the collection of independent column vectors ![]() of A satisfies the independent axioms of matroid. Thus,
of A satisfies the independent axioms of matroid. Thus, ![]() is a matroid and this matroid is denoted by
is a matroid and this matroid is denoted by![]() , where
, where ![]() is the set of all column vectors of A.
is the set of all column vectors of A.
Now, let G be a graph. Then ![]() is the matroid on the edge set
is the matroid on the edge set ![]() with the set of all cycles of G as circuit. This matroid is called the cycle matroid of G. Two matroids
with the set of all cycles of G as circuit. This matroid is called the cycle matroid of G. Two matroids ![]() and
and ![]() are isomorphic, denoted by
are isomorphic, denoted by![]() , if there is a bijection
, if there is a bijection ![]() from
from ![]() to
to ![]() such that, for all
such that, for all![]() ,
, ![]() is independent in
is independent in ![]() if and only if X is independent in
if and only if X is independent in![]() . A matroid that is isomorphic to the cycle matroid of a graph is called graphic. If M is isomorphic to
. A matroid that is isomorphic to the cycle matroid of a graph is called graphic. If M is isomorphic to ![]() for a matrix A over F, then M is called F-representable. In the sequel, by F we mean a finite field.
for a matrix A over F, then M is called F-representable. In the sequel, by F we mean a finite field.
We call an element e a loop of a matroid M if ![]() is a circuit of M. Moreover, if f and g are element of
is a circuit of M. Moreover, if f and g are element of ![]() such that
such that ![]() is a circuit, then f and g are said to be parallel in M. A parallel class of M is a maximal subset X of
is a circuit, then f and g are said to be parallel in M. A parallel class of M is a maximal subset X of ![]() such that any two distinct members X are parallel and no member of X is a loop. A parallel class is trivial if it contains just one element. If M has no loops and no non-trivial parallel classes, it is called a simple matroid or a combinatorial geometry.
such that any two distinct members X are parallel and no member of X is a loop. A parallel class is trivial if it contains just one element. If M has no loops and no non-trivial parallel classes, it is called a simple matroid or a combinatorial geometry.
2.2. Uniform Matroid Um,n
Let m and n be non-negative integers such that![]() . Let E be a set of cardinality n and
. Let E be a set of cardinality n and ![]() be all subsets of E of cardinality less than or equal to m. This is a matroid on E, called the uniform matroid of rank m and denoted by
be all subsets of E of cardinality less than or equal to m. This is a matroid on E, called the uniform matroid of rank m and denoted by![]() . By definition, the set of basis
. By definition, the set of basis ![]() of
of ![]() is
is![]() , and the set of circuits
, and the set of circuits ![]() is
is![]() .
.
2.3. Affine Matroid
Now, we are going to define affine matroid. A set ![]() is affinely dependent if
is affinely dependent if ![]() and there are elements
and there are elements ![]() of F, not all zero, such that
of F, not all zero, such that
![]() and
and![]() . It is easy to show that affine dependence of
. It is easy to show that affine dependence of
![]() is equivalent to each of the followings;
is equivalent to each of the followings;
(Ad1) ![]() is linearly dependent, where
is linearly dependent, where ![]() is the
is the ![]() - tuple of elements of F.
- tuple of elements of F.
(Ad2) ![]() is linearly dependent.
is linearly dependent.
A set ![]() is affinely independent if it is not affinely dependent.
is affinely independent if it is not affinely dependent.
Suppose that![]() . Let A be the
. Let A be the ![]() matrix over F, the i-th column of with is
matrix over F, the i-th column of with is![]() . The matroid
. The matroid ![]() is called an affine matroid over F. In particular, if
is called an affine matroid over F. In particular, if![]() , and
, and![]() , then the affine matroid is denoted by
, then the affine matroid is denoted by![]() . In general, if M is an affine matroid over
. In general, if M is an affine matroid over ![]() of rank
of rank![]() , where
, where![]() , then a subset X of
, then a subset X of ![]() is dependent in M if, in the representation of X by points in
is dependent in M if, in the representation of X by points in![]() , there are two identical points, or three collinear points, or four coplanar points, or five points in space. Hence the flats of M of ranks one, two, and three are represented geometrically by points, lines, and planar, respectively.
, there are two identical points, or three collinear points, or four coplanar points, or five points in space. Hence the flats of M of ranks one, two, and three are represented geometrically by points, lines, and planar, respectively.
We extend the use of diagram of affine matroid to represent arbitrary matroids of rank at most four. Generally, such diagrams are governed by the following rules. All loops are marked in a single inset. Parallel elements are represented by touching points. If three elements form a circuit, the corresponding points are collinear. Likewise, if four elements form a circuit, the corresponding points are coplanar. In such a diagram, the lines need not be straight and the planes may be twisted. Certain lines with fewer than three points on them will be marked as part of the indication of a plane, or as con- struction lines. We call such a diagram a geometric representation for the matroid.
Now we will define the projective geometry. Let V be a vector space over F. For each![]() ,
, ![]() if v and w lie on the same 1-dimensional subspace of V. Then, ~ is an equivalence relation on V and
if v and w lie on the same 1-dimensional subspace of V. Then, ~ is an equivalence relation on V and ![]() is called the projective space of V or projective geometry and will be denoted by
is called the projective space of V or projective geometry and will be denoted by![]() . For a matroid M, delete all the loops from M and then, for each non-trivial parallel class X, delete all but one distinguished element of X, the matroid we obtain is called the simple matroid associated with M and is denoted by
. For a matroid M, delete all the loops from M and then, for each non-trivial parallel class X, delete all but one distinguished element of X, the matroid we obtain is called the simple matroid associated with M and is denoted by![]() . Evidently the construction of
. Evidently the construction of ![]() from V is analoguous to the construction of the simple matroid
from V is analoguous to the construction of the simple matroid ![]() from a matroid M. It is clear that a matroid M is F-representable if and only if its associated simple matriod is F-representable. Hence, when we discuss representability questions, it is enough to concentrate on simple matroids.
from a matroid M. It is clear that a matroid M is F-representable if and only if its associated simple matriod is F-representable. Hence, when we discuss representability questions, it is enough to concentrate on simple matroids.
2.4. Projective Geometrices
If![]() , then
, then ![]() has dimension n and it is denoted by
has dimension n and it is denoted by![]() . In particular, when F is
. In particular, when F is![]() , it will be written
, it will be written ![]() for
for![]() . Let’s find the geometric representation of
. Let’s find the geometric representation of![]() . For each
. For each![]() , there are no non- zero elements except v on the 1-dimensional subspace of
, there are no non- zero elements except v on the 1-dimensional subspace of ![]() through v (Figure 1). Thus
through v (Figure 1). Thus
![]() .
.
It is easy to see ![]() and
and ![]() lie on the same line (plane) of
lie on the same line (plane) of ![]() (
(![]() ). Also,
). Also, ![]() and
and ![]() are circuits of
are circuits of![]() . Furthermore,
. Furthermore, ![]() is a circuit, because
is a circuit, because![]() . Thus the geo- metric representation of
. Thus the geo- metric representation of ![]() is Figure 2.
is Figure 2.
![]() is called the Fano matroid and will be denoted by
is called the Fano matroid and will be denoted by![]() . In
. In![]() ,
, ![]() is a circuit and a hyperplane. The matroid N obtained from
is a circuit and a hyperplane. The matroid N obtained from ![]() by relaxing the circuit hyperplane
by relaxing the circuit hyperplane ![]() is called non-Fano matroid and is denoted by
is called non-Fano matroid and is denoted by ![]() (Figure 3).
(Figure 3).
2.5. Duals of Representable Matroids
Give a ![]() matrix A by elementary row operations and interchanging two columns
matrix A by elementary row operations and interchanging two columns
or deleting a zero row. A can be transformed to a form![]() , where
, where ![]() is
is ![]() identity matrix and D is
identity matrix and D is ![]() matrix. It is clear that
matrix. It is clear that ![]() is isomorphic to
is isomorphic to![]() . We can show that the dual matroid
. We can show that the dual matroid ![]() of M is
of M is ![]() ( [9] ). Hence, the dual of F-representable matroid is F-representable. For example, let
( [9] ). Hence, the dual of F-representable matroid is F-representable. For example, let
![]()
be a matrix over![]() . Then, we can see that
. Then, we can see that ![]() is isomorphic to
is isomorphic to![]() .
.
![]()
and we can see that the set of circuits of ![]() is
is
![]() .
.
3. Minors
In this section, we define minors which are important to representability. For the definition of minor, we have to define contraction which is the dual of the operation of deletion. We can see that contraction for matroids generalizes the operation of contraction for graphs. Let M be a matroid on E and T be a subset of E. Then ![]() is called the contraction of T from M and also denoted by
is called the contraction of T from M and also denoted by![]() . For easy understanding, let us see what it means in graphic matroids. Let G be a graph
. For easy understanding, let us see what it means in graphic matroids. Let G be a graph
![]()
and![]() . Then, G/3 is the graph
. Then, G/3 is the graph
![]()
and ![]() is
is
![]()
Also ![]() is
is
![]()
and ![]() is
is
![]()
which is the same as G/3. Thus,
![]()
and we see that the contraction of a graphic matroid is the same as the matroid of the contracted graph, where we used ![]() for a planar graph G.
for a planar graph G.
Now let ![]() be the dual of a matroid M. Then the rank function
be the dual of a matroid M. Then the rank function ![]() of
of ![]() is given by
is given by ![]() ( [9] ). If
( [9] ). If![]() , the rank function of
, the rank function of ![]() is the restriction of
is the restriction of ![]() to the subset of
to the subset of![]() , that is, for all
, that is, for all![]() ,
, ![]() .
.
Proposition 3.1. If![]() , then for all
, then for all![]() ,
,![]() .
.
Proof. By definition,![]() . Thus
. Thus
![]()
because ![]() and
and![]() . □
. □
Proposition 3.2. Let ![]() be a basis for
be a basis for![]() . Then
. Then
![]()
Proof. For the convenience, let’s denote the equality by![]() . It is clear that
. It is clear that![]() . To show that
. To show that![]() , let
, let![]() . Then,
. Then, ![]() for some basis B of
for some basis B of![]() . Cleary
. Cleary ![]() is a basis of
is a basis of![]() . So
. So![]() . Thus
. Thus
![]()
and it was proved that![]() . Now if we show that
. Now if we show that![]() , the proof is completed. Let
, the proof is completed. Let![]() . Then
. Then
![]()
since ![]() is a basis of
is a basis of![]() . Hence
. Hence ![]() and
and![]() . □
. □
Proposition 3.3. If![]() , then
, then
1)![]() ,
,
2)![]() , and
, and
3)![]() .
.
Proof. 1)![]() . Thus
. Thus![]() .
.
2)![]() . 3) is obtained if we replace M by
. 3) is obtained if we replace M by ![]() in the left-
in the left-
hand side of 1). □
Now, let A be a matroid over F and T be a subset of the set E of column levels of A. We shall denote by ![]() the matrix obtained from A by deleting all the columns whose labels are in T. Clearly,
the matrix obtained from A by deleting all the columns whose labels are in T. Clearly,![]() . Moreover, by the following, we can see that the class of F-representable matroids is minor closed.
. Moreover, by the following, we can see that the class of F-representable matroids is minor closed.
Proposition 3.4. Every contraction of an F-representable matroid is F-representable.
Proof. The duals of F-representable matroid are F-representable. Since
![]() , we proved that a contraction of F-representable matroid is F-representable. □
, we proved that a contraction of F-representable matroid is F-representable. □
Now suppose that e is the label of a non-zero column of A. Then, by pivoting on a non-zero entry of e, we can transform A into a matrix ![]() in which the column labelled by e has single non-zero entry. In this case,
in which the column labelled by e has single non-zero entry. In this case, ![]() will denote the matrix obtained from
will denote the matrix obtained from ![]() by deleting the row and column containing the unique non-zero entry in e. Then, we have the following property.
by deleting the row and column containing the unique non-zero entry in e. Then, we have the following property.
Proposition 3.5.![]() .
.
Proof. It is enough to show that the second equation is true, because the first equation is clear. By using row and column swaps if necessary, ![]() can be considered as the matrix in which the unique nonzero entry of e is in row 1 and column 1. Let I be a k-element subset of the ground set of
can be considered as the matrix in which the unique nonzero entry of e is in row 1 and column 1. Let I be a k-element subset of the ground set of ![]() such that
such that![]() . Then the set of columns labelled by
. Then the set of columns labelled by ![]() is linearly independent if and only if the matrix B which has columns
is linearly independent if and only if the matrix B which has columns ![]() and the 1st column of it is the column corresponding to e has rank
and the 1st column of it is the column corresponding to e has rank![]() . This is equivalent to the matrix deleted row 1 and column 1 of B has rank k and this is equivalent to the columns of
. This is equivalent to the matrix deleted row 1 and column 1 of B has rank k and this is equivalent to the columns of ![]() labelled by I is linearly independent. Thus,
labelled by I is linearly independent. Thus,![]() .
.
□
4. Representability of P8
Now, we shall describe the construction of representations for matroids. Two matrices ![]() and
and ![]() are equivalent if
are equivalent if ![]() and
and ![]() are isomorphic. It is easy to see that if
are isomorphic. It is easy to see that if ![]() is a rank-r matroid, then A is equivalent to a standard matrix
is a rank-r matroid, then A is equivalent to a standard matrix![]() , where
, where ![]() is the
is the ![]() identity matrix. Given such a matrix, let its columns be labelled in order,
identity matrix. Given such a matrix, let its columns be labelled in order,![]() . Let B be the basis
. Let B be the basis ![]() of
of![]() . For all i in
. For all i in![]() , the unique non-zero entry in column i of
, the unique non-zero entry in column i of ![]() is in row i. Thus it is natural to label the rows of
is in row i. Thus it is natural to label the rows of ![]() by
by![]() . Hence, D has its rows labelled by
. Hence, D has its rows labelled by ![]() and its columns labelled by
and its columns labelled by![]() . For all
. For all![]() , there exists a unique circuit
, there exists a unique circuit ![]() contained in
contained in![]() . In fact,
. In fact,
![]() .
. ![]() is called the B-fundamental circuit of
is called the B-fundamental circuit of![]() . Let
. Let ![]() be the matrix obtained from D by replacing each non-zero entry of D by 1. Then the columns of
be the matrix obtained from D by replacing each non-zero entry of D by 1. Then the columns of ![]() are precisely the incidence vectors of the sets
are precisely the incidence vectors of the sets![]() . This matrix
. This matrix ![]() is called the B-fundamental-circuit incidence matrix of
is called the B-fundamental-circuit incidence matrix of![]() . Now let
. Now let ![]() be a rank-r matroid and B be a basis
be a rank-r matroid and B be a basis ![]() for M. Let X be the B -fundamental-circuit incidence matrix of M. And let columns of X be labelled by
for M. Let X be the B -fundamental-circuit incidence matrix of M. And let columns of X be labelled by![]() . Then,
. Then,![]() . Thus the task of finding an F-representation for M can be viewed as being one of finding the specific elements of F that correspond to the non-zero elements of
. Thus the task of finding an F-representation for M can be viewed as being one of finding the specific elements of F that correspond to the non-zero elements of![]() . We can see that most of the entries of D can be predetermined by the following Proposition 4.1. Before stating it, we shall require some preliminaries.
. We can see that most of the entries of D can be predetermined by the following Proposition 4.1. Before stating it, we shall require some preliminaries.
Let the rows of ![]() be indexed by
be indexed by ![]() and its columns by
and its columns by![]() . Let
. Let ![]() denote the associated simple bipartite graph, that is,
denote the associated simple bipartite graph, that is, ![]() has vertex classes
has vertex classes ![]() and
and ![]() and two vertices
and two vertices ![]() and
and ![]() are ad- jacent if and only if the entry in row
are ad- jacent if and only if the entry in row ![]() and column
and column ![]() of
of ![]() is 1. For example, if
is 1. For example, if
![]()
then ![]() is
is
![]()
We have a nice way for representing matroid;
Proposition 4.1. Let the ![]() matrix
matrix ![]() be an F-representation for the matroid M. Let
be an F-representation for the matroid M. Let ![]() be a basis of the cycle matroid of
be a basis of the cycle matroid of![]() . Then
. Then![]() , where
, where ![]() is the number of connected component of
is the number of connected component of![]() . Moreover, if
. Moreover, if ![]() is an ordered k-tuple of non-zero elements of F, then M has an F-representation
is an ordered k-tuple of non-zero elements of F, then M has an F-representation ![]() that is equivalent to
that is equivalent to ![]() such that, for each i in
such that, for each i in![]() , where the entry of
, where the entry of ![]() corresponding to
corresponding to ![]() is
is ![]() ( [9] [10] ).
( [9] [10] ).
By the above proposition, we can find the fields on which given matroid is re- presentable.
Example 4.2. ![]() is the matroid whose geometric representation is the following Figure 4.
is the matroid whose geometric representation is the following Figure 4.
Let ![]() be a representation over
be a representation over ![]() of
of![]() . Then
. Then
![]()
Thus, the associated simple bipartite graph ![]() is
is
![]()
and a basis of ![]() is
is
![]()
Therefore, ![]() is equivalent to the form of
is equivalent to the form of
![]()
![]()
Figure 4. Geometric representation of P6.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,![]() .
.
We want to find the fields ![]() in which the negative equations satisfy. It is easy to see that the equations have no solution if
in which the negative equations satisfy. It is easy to see that the equations have no solution if ![]() is equal to
is equal to ![]() or
or![]() . In case of
. In case of![]() , let’s check if the equations have a common solution. There are three cases;
, let’s check if the equations have a common solution. There are three cases;
1)![]() .
.
If![]() , then
, then![]() . Thus,
. Thus, ![]() and
and![]() . Hence, we don’t have a solution.
. Hence, we don’t have a solution.
2)![]() .
.
In this case, ![]() and
and![]() . Thus, there are no solution.
. Thus, there are no solution.
3)![]() .
.
In this case, ![]() and
and![]() . Thus we have no solution.
. Thus we have no solution.
In![]() , if
, if![]() , then
, then ![]() and
and ![]() . Therefore we showed that
. Therefore we showed that ![]() is representable over F if and only if
is representable over F if and only if![]() .
.
Example 4.3. If
![]()
is the matrix over F with![]() , then it is easy to see that
, then it is easy to see that ![]() by Figure 3. Also, if
by Figure 3. Also, if ![]() is a matrix over F and
is a matrix over F and![]() , then
, then
![]()
By taking a basis of![]() ,
, ![]() is equivalent to a matrix
is equivalent to a matrix
![]()
Since![]() . Also, because
. Also, because ![]() and
and ![]() ,
,![]() . Thus
. Thus![]() .
.
Since![]() ,
,![]() . Therefore, we showed that
. Therefore, we showed that ![]() is repre- sentable over F if and only if
is repre- sentable over F if and only if![]() .
. ![]() is the matroid of the matrix
is the matroid of the matrix
![]()
over![]() . It’s geometric representation is the following Figure 5.
. It’s geometric representation is the following Figure 5.
Lemma 4.4. ![]() is representable over a field F if and only if
is representable over a field F if and only if![]() .
.
Proof. If![]() , then the B-fundamental circuit incidence matrix of
, then the B-fundamental circuit incidence matrix of ![]() is
is
![]()
By taking a basis of![]() , A is equivalent to a matrix
, A is equivalent to a matrix![]() , where
, where
![]()
![]()
Figure 5. Geometric representation of P7.
Because ![]() and
and ![]() and
and![]() .
.
As![]() . Therefore
. Therefore
![]()
where![]() . Therefore, we proved that
. Therefore, we proved that ![]() is representable over F if and only if
is representable over F if and only if![]() . □
. □
Non F-representable matroid for which every proper minor is F-representable is called the excluded or forbidden minor for F-representability. Because a matroid M is F-representable if and only if all its minors are F-representable (Proposition 3.5), finding the complete set of excluded minors for F-representability is the solution for the F-representability. Since the duals of F-representable matroid are F-representable, the dual of an excluded minor for F-representability is an excluded minor for F-representability.
To find an excluded minor for ![]() -representability, we need the following property:
-representability, we need the following property:
Proposition 4.5. Let F be a field and k be an integer exceeding 1. Then uniform matroid ![]() is F-representable if and only if
is F-representable if and only if![]() .
.
Proof. Let![]() , where A is a
, where A is a ![]() matrix. We can consider A as a matrix
matrix. We can consider A as a matrix
![]()
where ![]() are non-zero different elements of F. Thus, it should be
are non-zero different elements of F. Thus, it should be ![]() and so
and so![]() . Conversely, if
. Conversely, if![]() , then
, then ![]() and we can choose non-zero different
and we can choose non-zero different ![]() -elements of F.
-elements of F.
□
From the above proposition, we can see that ![]() and
and ![]() are excluded minors for GF(q)-representability. In 1958, Tutte showed that
are excluded minors for GF(q)-representability. In 1958, Tutte showed that ![]() is the only excluded minor for
is the only excluded minor for ![]() -representability ( [2] ). The problem of finding the com- plete set of excluded minors for
-representability ( [2] ). The problem of finding the com- plete set of excluded minors for ![]() -representability was solved by Bixby and Seymour in 1979 ( [3] [4] ). The set is
-representability was solved by Bixby and Seymour in 1979 ( [3] [4] ). The set is![]() .
.
By Proposition 4.5, it is easy to see that ![]() and
and ![]() are excluded minors for GF(4)-representability. In Examples 4.2 and 4.3, we can see that
are excluded minors for GF(4)-representability. In Examples 4.2 and 4.3, we can see that ![]() and
and ![]() are not GF(4)-representable. It is not difficult to see that every proper minor of them is GF(4)-representable. Thus
are not GF(4)-representable. It is not difficult to see that every proper minor of them is GF(4)-representable. Thus ![]() and
and ![]() are excluded minors for GF(4)-represent- ability. Clearly
are excluded minors for GF(4)-represent- ability. Clearly ![]() is self-dual.
is self-dual.
Let
![]()
be the matrix over![]() . Then,
. Then, ![]() is the matroid
is the matroid![]() .
.
Lemma 4.6. ![]() is representable over a field F if and only if
is representable over a field F if and only if![]() .
.
Proof. Let ![]() be an F-representation for
be an F-representation for![]() . If
. If![]() , then the B- fundamental circuit incidence matrix for
, then the B- fundamental circuit incidence matrix for ![]() is
is
![]()
By choosing a basis for![]() , we can consider
, we can consider
![]()
Because ![]() and
and ![]() and
and![]() . Substituting these to the matrix D, we have
. Substituting these to the matrix D, we have
![]()
From the circuits![]() ,
, ![]() ,
, ![]() and
and![]() , we get the equations
, we get the equations
![]()
From the first and fourth equation, we get![]() . Substituting b for d in the second and third equation, we get
. Substituting b for d in the second and third equation, we get ![]() and
and![]() . As
. As![]() , it follows that
, it follows that ![]() and
and![]() . Because
. Because![]() ,
,![]() . Thus
. Thus
![]()
In fact, we can show that ![]() □
□
For a matroid M, an automorphism is a permutation ![]() of
of ![]() such that
such that ![]() for all
for all![]() . The set of automorphisms of M forms a group under composition. This automorphism is transitive if, for every two elements x and y of
. The set of automorphisms of M forms a group under composition. This automorphism is transitive if, for every two elements x and y of![]() , there is an automorphism that maps x to y.
, there is an automorphism that maps x to y.
Lemma 4.7. The automorphism group of ![]() acts transitively on
acts transitively on![]() .
.
Proof. We can see that the geometric representation of ![]() is the following Figure 6
is the following Figure 6
because ![]() has only 10 4-circuits
has only 10 4-circuits ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and![]() . From the geometric representation of
. From the geometric representation of![]() , it is easy to see that the permutations
, it is easy to see that the permutations ![]() and
and ![]() are both automorphisms of
are both automorphisms of![]() . For example,
. For example, ![]() and
and ![]() are the following Figure 7 and Figure 8.
are the following Figure 7 and Figure 8.
Thus the automorphism group of ![]() is
is![]() .
.
Any two elements in ![]() and
and ![]() can be mapped to each other by an automorphism in
can be mapped to each other by an automorphism in![]() . Similarly, any two elements in
. Similarly, any two elements in ![]() and
and ![]() can be mapped to each other by an automorphism in
can be mapped to each other by an automorphism in![]() . For the remaining two elements of
. For the remaining two elements of![]() , they are mapped each other by the following;
, they are mapped each other by the following;![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]()
Figure 6. Geometric representation of P8.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Thus, the automorphism group of ![]() acts transitively on
acts transitively on![]() .
.
□
Now, we get the following result, which is the purpose of this paper.
Theorem 4.8. ![]() is an excluded minor for GF(4)-representability.
is an excluded minor for GF(4)-representability.
Proof. By Lemma 4.6, ![]() is not
is not ![]() representable. Because the automorphism group of
representable. Because the automorphism group of ![]() acts transitively on
acts transitively on ![]() by Lemma 4.7, for any element e of
by Lemma 4.7, for any element e of![]() , we have
, we have![]() .
.
By Proposition 3.5,![]() . Because
. Because
![]()
![]() . But, since
. But, since ![]() is representable over
is representable over ![]() by Lemma 4.4, every contraction of
by Lemma 4.4, every contraction of ![]() is GF(4)-representable. By Proposition 3.3(1), for each element
is GF(4)-representable. By Proposition 3.3(1), for each element![]() ,
,![]() . Because
. Because ![]() is self-dual,
is self-dual,![]() . Thus
. Thus
![]() . Hence, every deletion of
. Hence, every deletion of ![]() is GF(4)-representable. Therefore, every proper minor of
is GF(4)-representable. Therefore, every proper minor of ![]() is GF(4)-representable and we proved that
is GF(4)-representable and we proved that ![]() is an excluded minor for GF(4)-representability. □
is an excluded minor for GF(4)-representability. □
Cite this paper
Ahn, S. and Han, B. (2016) Excluded Minority of P8 for GF(4)- Representability. Open Journal of Discrete Mathematics, 6, 279-296. http://dx.doi.org/10.4236/ojdm.2016.64024
References
- 1. Whitney, H. (1935) On the Abstract Properties of Linear Dependence. The American Journal of Mathematics, 57, 509-533.
http://dx.doi.org/10.2307/2371182
- 2. Tutte, W.T. (1958) A Homotopy Theorem for Matroids, I, II. Transactions of the American Mathematical Society, 88, 144-174.
http://dx.doi.org/10.2307/1993244
- 3. Bixby, R.E. (1979) On Reid’s Characterization of the Ternary Matroids. Journal of Combinatorial Theory, Series B, 26, 174-204.
http://dx.doi.org/10.1016/0095-8956(79)90056-X
- 4. Seymour, P.D. (1979) Matroid Representation over GF(3). Journal of Combinatorial Theory, Series B, 26, 159-173.
http://dx.doi.org/10.1016/0095-8956(79)90055-8
- 5. Kahn, J. and Seymour, P. (1988) On Forbidden Minors for GF(3). Proceedings of the American Mathematical Society, 102, 437-440.
http://dx.doi.org/10.2307/2045902
- 6. Oxley, J.G. (1986) On the Matroids Representable over GF(4). Journal of Combinatorial Theory, Series B, 41, 250-252.
http://dx.doi.org/10.1016/0095-8956(86)90049-3
- 7. Geelen, J.F., Gerards, A.M.H. and Kapoor, A. (2000) The Excluded Minors for GF(4)-Re-presentable Matroids. Journal of Combinatorial Theory, Series B, 79, 247-299.
http://dx.doi.org/10.1006/jctb.2000.1963
- 8. Rota, G.-C. (1970) Combinatorial Theory, Old and New. Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 3, 229-233.
- 9. Oxley, J.G. (1992) Matroid Theory, Oxford Science Publications. The Clarendon Press, Oxford University Press, New York.
- 10. Brylawski, T.H. and Lucas, D. (1976) Uniquely Representable Combinatorial Geometries. In Terie combinatorie (Proc. 1973 Internat. Colloq), Academic Nazionale dei Lincei, Rome 83-104.




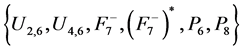 is the complete set of GF(4)-representability. In this paper, we show that
is the complete set of GF(4)-representability. In this paper, we show that  is an excluded minor for GF(4)-representability.
is an excluded minor for GF(4)-representability.
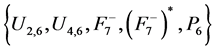 is the complete set of ex- cluded minors for GF(4)-representability. Oxley showed that the conjecture is wrong by showing
is the complete set of ex- cluded minors for GF(4)-representability. Oxley showed that the conjecture is wrong by showing 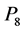 is also excluded minor for GF(4)-representability in his brief note [6] . Geelen, Gerarads and Kapoor proved that it is enough to add
is also excluded minor for GF(4)-representability in his brief note [6] . Geelen, Gerarads and Kapoor proved that it is enough to add 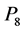 to the list of Kahn and Seymour [7] . It is not an easy problem to find the excluded minors for GF(q)- representability when q is more than 4. Instead, we have the conjecture by Rota that the number of excluded minors are finite for any prime powers q [8] . In this paper, we study the properties of minor and show that
to the list of Kahn and Seymour [7] . It is not an easy problem to find the excluded minors for GF(q)- representability when q is more than 4. Instead, we have the conjecture by Rota that the number of excluded minors are finite for any prime powers q [8] . In this paper, we study the properties of minor and show that 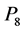 is excluded minor for GF(4)- representability deliberately.
is excluded minor for GF(4)- representability deliberately. of subsets of E satisfying the following three conditions:
of subsets of E satisfying the following three conditions: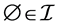 .
.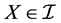 and
and 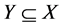 then
then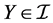 .
.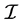 and
and , then there exists
, then there exists 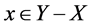 such that
such that 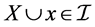 .
.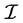 of vectors of V,
of vectors of V, 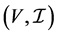 is a matroid. If
is a matroid. If 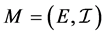 is a matroid, M is called a matroid on E. Also E which is denoted by
is a matroid, M is called a matroid on E. Also E which is denoted by 















































































































































































































































































































































































































































































































































































































