Received 28 September 2015; accepted 9 April 2016; published 12 April 2016

ABSTRACT

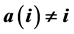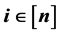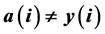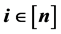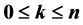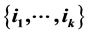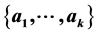Let n be a positive integer. A permutation a of the symmetric group of permutations of is called a derangement if for each. Suppose that x and y are two arbitrary permutations of. We say that a permutation a is a double derangement with respect to x and y if and for each. In this paper, we give an explicit for- mula for, the number of double derangements with respect to x and y. 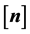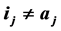Let and let and be two subsets of with and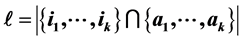. Suppose that 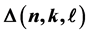denotes the number of derangements x such that. As the main result, we show that if and z is a permutation such that for and for, then where .

Keywords:

Symmetric Group of Permutations, Derangement, Double Derangement

1. Introduction

Let n be a positive integer. A derangement is a permutation of the symmetric group of permutations of such that none of the elements appear in their original position. The number of derangements of is denoted by or n¡. A simple recursive argument shows that

The number of derangements also satisfies the relation. It can be proved by the inclusion-

exclusion principle that is explicitly determined by. This implies that.

These facts and some other results concerning derangements can be found in [1] . There are also some generalizations of this notion. The problème des rencontres asks how many permutations of the set have

exactly k fixed points. The number of such permutations is denoted by and is given by. Thus, we can say that. Some probabilistic aspects of this concept and the related notions

concerning the permutations of is discussed in [2] and [3] .

Let e be the identity element of the symmetric group, which is defined by for each. We can say that a permutation a of is a derangement if for each. We denote this by. Thus, is the number of a with. If c is any fixed element of then the number of with is also, since if and only if. In the present paper, we extend the concept of a derangement to a double derangement with respect to two fixed elements x and y of.

2. The Result

In the following, we assume that n is a positive integer and the identity permutation of the symmetric group of permutations of is denoted by e. Moreover, for two permutations a and b of, the notation means that for each. We also denote the number of elements of a set A by.

Definition 1. Suppose that x and y are two arbitrary permutations of. We say that a permutation a is a double derangement with respect to x and y if and. The number of double derangements with respect to x and y is denoted by.

Proposition 1. Let and let and be two subsets of with and. Then, the number of derangements x such that, is determined by

Proof. Let. Thus for some. Now there are two cases:

Case 1.. Let. In this case a derangement x satisfies the condition if and only if the derangement of the set satisfies the condition for all, where for and. This provides a one to one correspondence between the derangements x of with for the given sets and with elements in their intersections, and the derangements of with for the given sets and with elements in their intersections.

Case 2.. In this case a derangement x satisfies the condition if and only if the derangement of the set satisfies the condition for all. This provides a one to one correspondence between the derangements x of with for the given sets and with elements in their intersections, and the derangements of with for the given sets and with elements in their intersections.

These considerations show that. Iterating this argument, we have

We can therefore assume that. We thus evaluate, where. For, we obviously have. For, we claim that

For a derangement x satisfying there are two cases: or.

If the first case occurs then we have to evaluate the number of derangements of the set for the given sets and with 0 elements in their intersections. The number is equal to.

If the second case occurs then we have to evaluate the number of derangements of the set for the given sets and with 0 elements in their intersections. The number is equal to.

We now use induction on k to show that

For we have

Now let the result be true for. We can write

Corollary 1. Let k be a positive integer. Then

Proof. Let, and for. Then a derangement x satisfies the condition if and only if defined by for is a permutation of. The number of such permutations is.

The following Table 1 gives some small values of.

The following lemma can be easily proved.

Lemma 1. Let x and y be two arbitrary permutations and be the number of i’s for which. Then there is a permutation z such that for and for and.

Theorem 2. Let and let z be a permutation such that for and for. Then

where.

Proof. Let be the set of all derangements x for which, where. Then

. We use the inclusion-exclusion principle to determine. For each

and we have

where. This implies the result.

Our ultimate goal is to find an explicit formula for evaluating for an arbitrary cycle c. Prior to that we need to state two elementary enumerative problems concerning subsets A of the set with k elements and exactly consecutive members.

Lemma 2. Let be the number of subsets of for which the equation has exactly solutions for r and s in A. If then

Moreover, and for other values of.

Proof. We can restate the problem as follows: We want to put k ones and zeros in a row in such a way that there are exactly appearance of one-one. To do this we put zeros and choose places of

the possible places for putting blocks of ones in ways. Let the number of ones in

the i-th block be. We then must have. The number of solutions for the latter equation is

.

Now suppose that we write around a circle. We thus assume that 1 is after n and so is also assumed to be consecutive. Under this assumption we have the following result.

Lemma 3. Let be the number of subsets of for which the equation (mod n) has exactly solutions for r and s in A. If then

Moreover, and for other values of.

Proof. Similar to the above argument, we want to put k ones and zeros around a circle in such a way that there are exactly appearances of one-one. At first, we put them in a row. There are four cases:

Case 1. There is no block of ones before the first zero and after the last zero. In this case we put zeros

and choose places of the possible places for putting blocks of ones in

ways. Let the number of ones in the i-th block be. We then must have. The number of

solutions for the latter equation is.

Case 2. There is no block of ones before the first zero but there is a block after the last zero. In this case we put zeros and choose places of the possible places for putting blocks of

ones in ways. Let the number of ones in the i-th block be. We then must have

. The number of solutions for the latter equation is.

Case 3. There is a block of ones before the first zero but there is no block after the last zero. This is similar to the above case.

Case 4. There is a block of ones before the first zero and a block of ones after the last zero. In this case we must have appearance of one-one in the row format, since we want to achieve appearance of one-one in the circular format. Thus we put zeros and choose places of the possible

places for putting blocks of ones in ways. Let the number of ones in the i-th block be. We then must have. The number of solutions for the latter equation is.

These considerations prove that

A straightforward computation gives the result.

The following Table 2 gives some small values of.

Theorem 3. Let c be be a cycle of length. Then

Proof. Let be the cycle defined by for, and for. Then.

Using the notations of Theorem 2, if and only if the subset of has exactly solutions for the equation (mod n) for in A. Thus the number of with the property is. Applying Theorem 2, we have the result.

Example 1. We evaluate and. Applying Theorem 3 with we have

and for the 13 double derangements x with respect to e and are

Applying Theorem 3 with we have

and for the 19 double derangements with respect to e and are

The above example shows that how can we evaluate for a cycle c. Moreover, Theorem 2 gives a formula for evaluating for any permutation z. Applying Lemma 1, we can compute for any permutations x and y.

Cite this paper

Pooya Daneshmand,Kamyar Mirzavaziri,Madjid Mirzavaziri, (2016) Double Derangement Permutations. Open Journal of Discrete Mathematics,06,99-104. doi: 10.4236/ojdm.2016.62010

References