Open Journal of Discrete Mathematics
Vol.3 No.3(2013), Article ID:34512,8 pages DOI:10.4236/ojdm.2013.33026
Some Results on Generalized Degree Distance
Department of Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, Tehran, Iran
Email: *iranmanesh@modares.ac.ir
Copyright © 2013 Asma Hamzeh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 14, 2013; revised February 15, 2013; accepted May 14, 2013
Keywords: Generalized Degree Distance; Cartesian Product; Join; Symmetric Difference; Composition; Disjunction
ABSTRACT
In [1], Hamzeh, Iranmanesh Hossein-Zadeh and M. V. Diudea recently introduced the generalized degree distance of graphs. In this paper, we present explicit formulas for this new graph invariant of the Cartesian product, composition, join, disjunction and symmetric difference of graphs and introduce generalized and modified generalized degree distance polynomials of graphs, such that their first derivatives at x = 1 are respectively, equal to the generalized degree distance and the modified generalized degree distance. These polynomials are related to Wiener-type invariant polynomial of graphs.
1. Introduction
A graph invariant is any function on a graph that does not depend on a labeling of its vertices. Topological indices and graph invariants based on the distances between the vertices of a graph are widely used in theoretical chemistry to establish relations between the structures and the properties of molecules. Topological indices provide correlations with physical, chemical and thermodynamic parameters of chemical compounds [2]. In this paper, we only consider simple and connected graphs. Let G be a graph on n vertices and 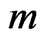 edges. We denote the vertex and the edge set of G by
edges. We denote the vertex and the edge set of G by 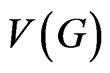 and
and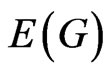 , respectively. As usual, the distance between the vertices
, respectively. As usual, the distance between the vertices 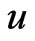 and
and 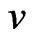 of G, denoted by
of G, denoted by 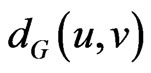 (
(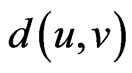 for short), is defined as the length of a minimum path connecting them. We let
for short), is defined as the length of a minimum path connecting them. We let 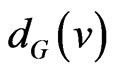 be the degree of a vertex
be the degree of a vertex 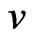 in G. The eccentricity, denoted by
in G. The eccentricity, denoted by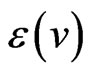 , is defined as the maximum distance from vertex
, is defined as the maximum distance from vertex 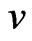 to any other vertex. The diameter of a graph G, denoted by
to any other vertex. The diameter of a graph G, denoted by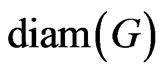 , is the maximum eccentricity over all vertices in a graph G.
, is the maximum eccentricity over all vertices in a graph G.
The Cartesian product 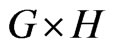 of graphs G and H is a graph such that
of graphs G and H is a graph such that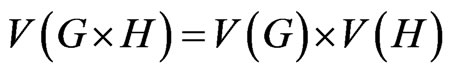 , and any two vertices
, and any two vertices 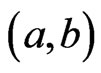 and
and 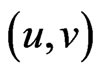 are adjacent in
are adjacent in 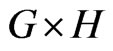 if and only if either
if and only if either 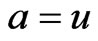 and
and 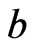 is adjacent to
is adjacent to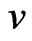 , or
, or 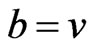 and
and 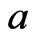 is adjacent to
is adjacent to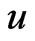 , see [3] for details. Let
, see [3] for details. Let 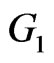 and
and 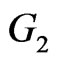 be two graphs with disjoint vertex sets
be two graphs with disjoint vertex sets 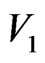 and
and  and edge sets
and edge sets 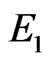 and
and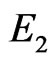 . The join
. The join 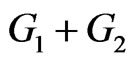 is the graph union
is the graph union 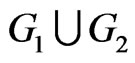 together with all the edges joining
together with all the edges joining 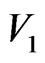 and
and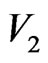 . The composition
. The composition 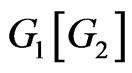 is the graph with vertex set
is the graph with vertex set 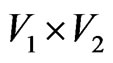 and
and 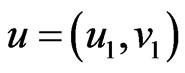 is adjacent to
is adjacent to 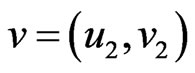 whenever (
whenever (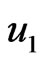 is adjacent with
is adjacent with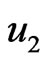 ) or (
) or (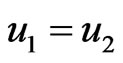 and
and 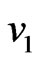 is adjacent to
is adjacent to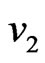 ), [3, p. 185]. The disjunction
), [3, p. 185]. The disjunction  of graphs
of graphs 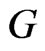 and
and 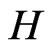 is the graph with vertex set
is the graph with vertex set 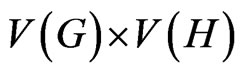 and
and 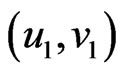 is adjacent to
is adjacent to 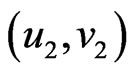 whenever
whenever 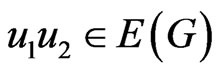 or
or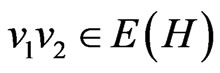 . The symmetric difference
. The symmetric difference  of two graphs
of two graphs 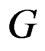 and
and 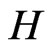 is the graph with vertex set
is the graph with vertex set 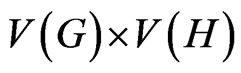 and
and
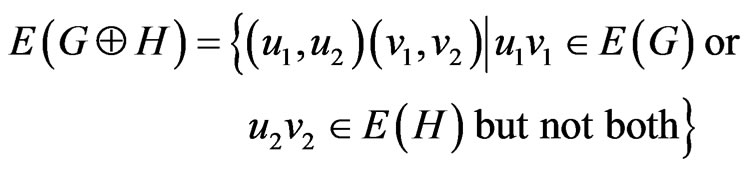 .
.
The first Zagreb index was originally defined as
 [4]. The first Zagreb index can be also expressed as a sum over edges of
[4]. The first Zagreb index can be also expressed as a sum over edges of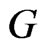 ,
,
 We refer readers to [5]
We refer readers to [5]
for the proof of this fact and for more information on Zagreb index. The first Zagreb coindex of a graph  is defined in [6] as:
is defined in [6] as:
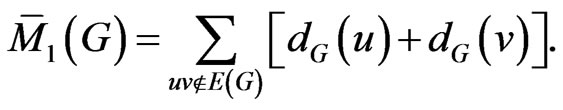
Let  be the number of pairs of vertices of a graph
be the number of pairs of vertices of a graph 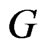 that are at distance
that are at distance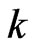 ,
, 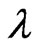 be a real numberand
be a real numberand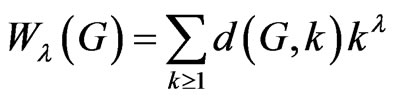 , that is called the Wienertype invariant of
, that is called the Wienertype invariant of 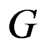 associated to
associated to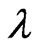 , see [7,8] for details. Additively weighted Harary index is defined in [9] as
, see [7,8] for details. Additively weighted Harary index is defined in [9] as
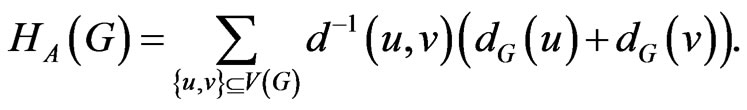
Dobrynin and Kochetova in [10] and Gutman in [11] introduced a new graph invariant with the name degree distance that is defined as follows:
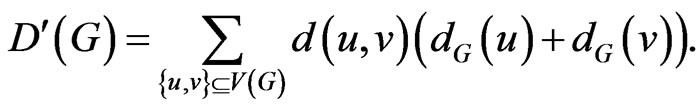
In [12], the modified degree distance was defined as follows:
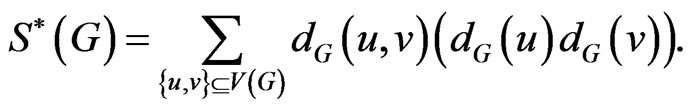
The generalized degree distance, denoted by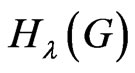 , is defined as follows in [1].
, is defined as follows in [1].
For every vertex 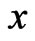 and real number
and real number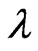 ,
, 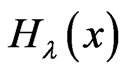 is defined by
is defined by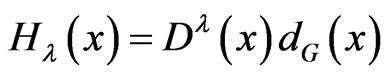 , where
, where
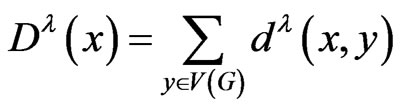 . We then define
. We then define
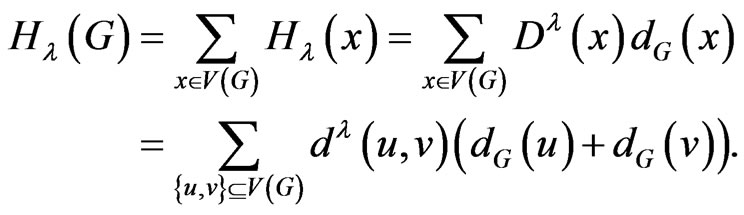
If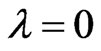 , then
, then . When
. When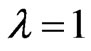 , this new topological index
, this new topological index 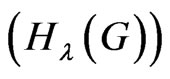 is equal to the degree distance (or Schultz index). There are many papers for studying this topological index, for example see [13-16]. Also if
is equal to the degree distance (or Schultz index). There are many papers for studying this topological index, for example see [13-16]. Also if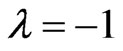 , then
, then 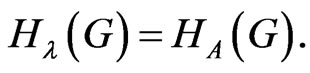 Therefore the study of this new topological index is important and we try to obtain some new results related to this topological index. The modified generalized degree distance, denoted by
Therefore the study of this new topological index is important and we try to obtain some new results related to this topological index. The modified generalized degree distance, denoted by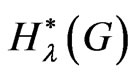 , is defined in [1] as:
, is defined in [1] as:
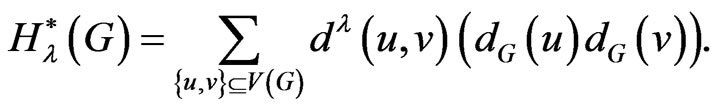
If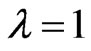 , then
, then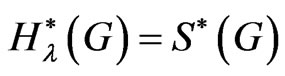 .
.
We construct graph polynomials having the property such that their first derivatives at 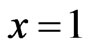 are equal to the generalized degree distance, the modified generalized degree distance and Wiener-type invariant respectively. These polynomials are defined as follows:
are equal to the generalized degree distance, the modified generalized degree distance and Wiener-type invariant respectively. These polynomials are defined as follows:
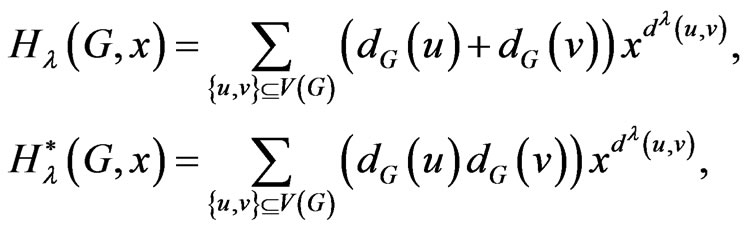
and

The Wiener index of the Cartesian product of graphs was studied in [17,18]. In [19], Klavžar, Rajapakse and Gutman computed the Szeged index of the Cartesian product of graphs. In [9,20-24], exact formulae for the hyper-Wiener, the first Zagreb index, the second Zagreb index and Schultz polynomials of some graph operations were computed.
Throughout this paper,  and
and 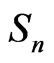 denote the cycle, path, complete graph and star on
denote the cycle, path, complete graph and star on 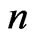 vertices. The complement of a graph
vertices. The complement of a graph 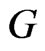 is a graph
is a graph 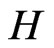 on the same vertices such that two vertices of
on the same vertices such that two vertices of 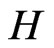 are adjacent if and only if they are not adjacent in
are adjacent if and only if they are not adjacent in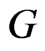 . The graph
. The graph 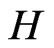 is usually denoted by
is usually denoted by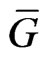 . Our other notations are standard and taken mainly from [2,25,26].
. Our other notations are standard and taken mainly from [2,25,26].
In this paper we present explicit formulas for 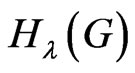 of graph operations containing the Cartesian product, composition, join, disjunction and symmetric difference of graphs and introduce generalized and modified generalized degree distance polynomials of graphs, such that their first derivatives at
of graph operations containing the Cartesian product, composition, join, disjunction and symmetric difference of graphs and introduce generalized and modified generalized degree distance polynomials of graphs, such that their first derivatives at 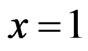 are respectively, equal to the generalized degree distance and the modified generalized degree distance. These polynomials are related with Wiener-type invariant polynomial of graphs.
are respectively, equal to the generalized degree distance and the modified generalized degree distance. These polynomials are related with Wiener-type invariant polynomial of graphs.
2. Main Results
The aim of this section is to compute the generalized degree distance for five graph operations. We start with a lemma which gives some information about the number of vertices and edges of operations on two arbitrary graphs. For a given graph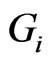 , the number of vertices and edges will be denoted by
, the number of vertices and edges will be denoted by 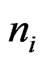 and
and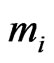 , respectively.
, respectively.
Lemma 2.1. [3,20] Let 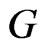 and
and 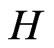 be graphs. Then we have:
be graphs. Then we have:
a)
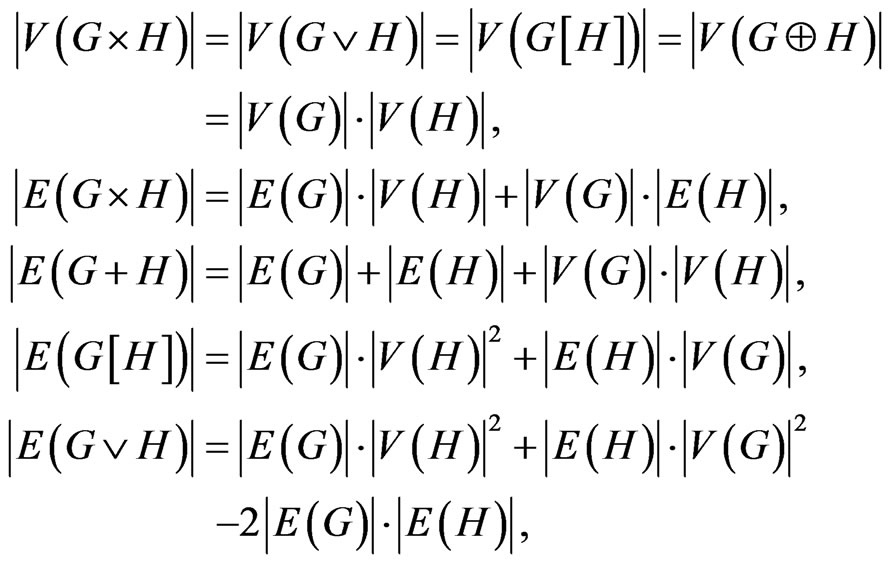
and
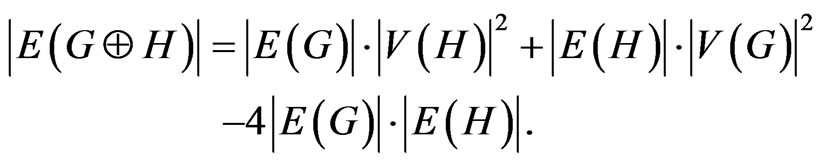
b) The graph 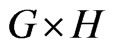 is connected if and only if
is connected if and only if 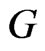 and
and 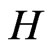 are connected.
are connected.
c) If 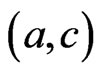 and
and 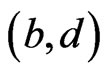 are vertices of
are vertices of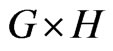 , then
, then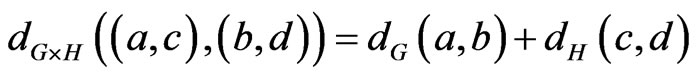 .
.
d) The Cartesian product, join, composition, disjunction and symmetric difference of graphs are associative and all of them are commutative except the composition of graphs.
e)
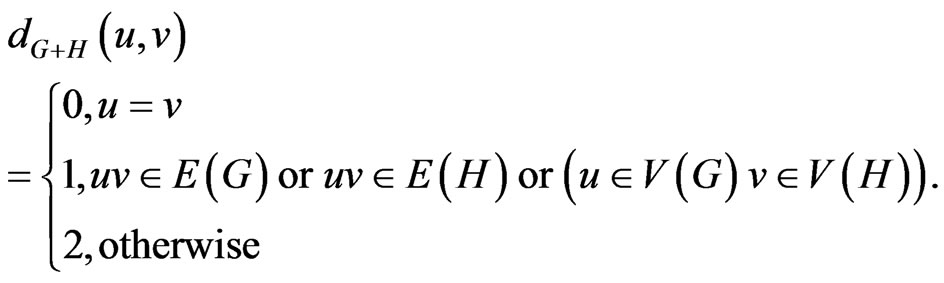 .
.
f)
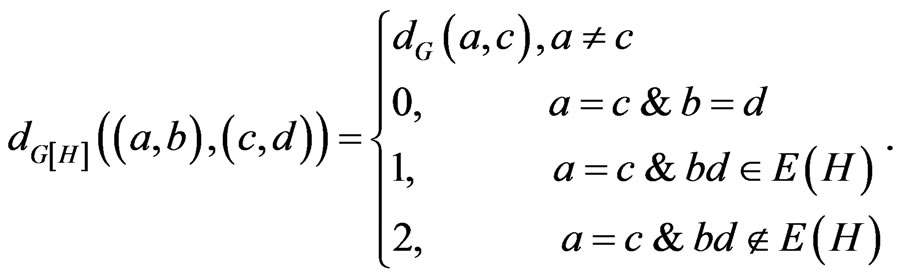
g)
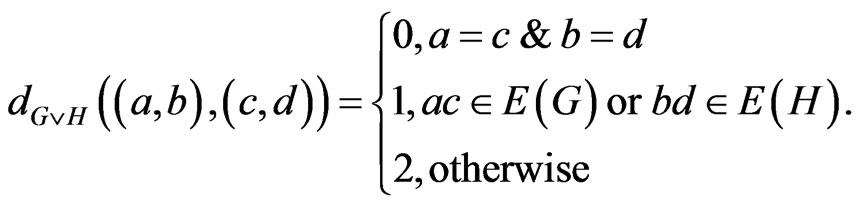
h)
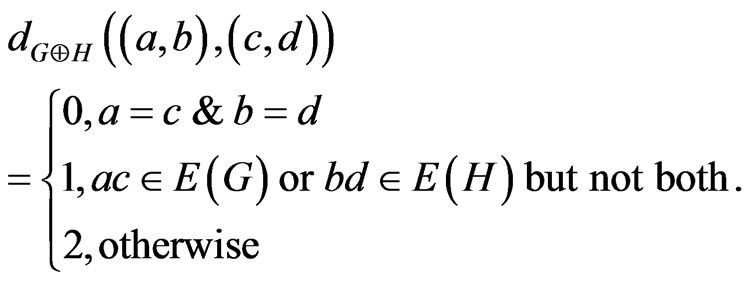
i) 
j) 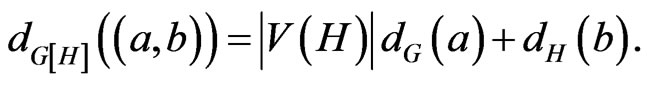
k) 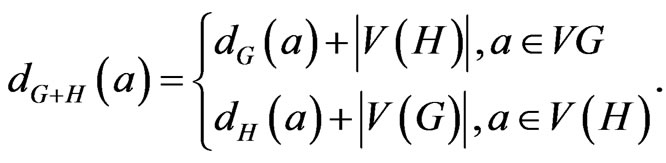
l)
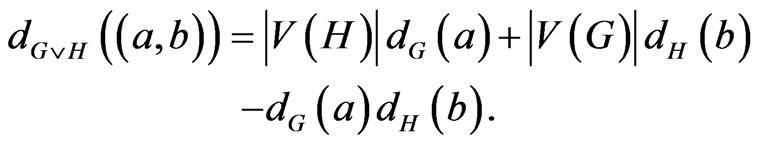
m)
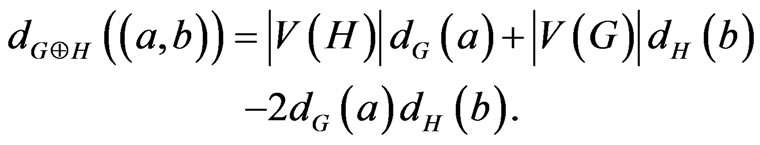
In Theorem 2.2, we give a formula for the generalized degree distance of the join of two graphs.
Theorem 2.2. Let  and
and 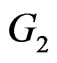 be two graphs. Then
be two graphs. Then
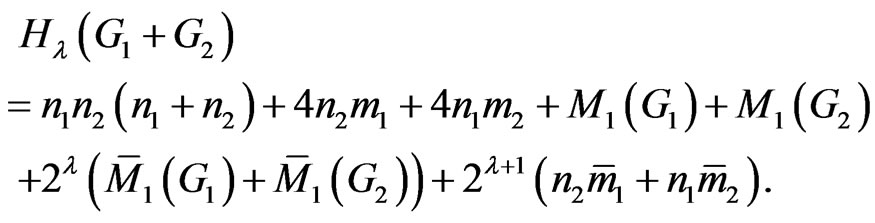
Proof. It is obvious from definition that for any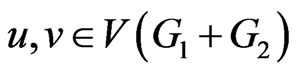 , the distance
, the distance 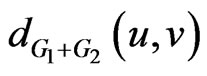 is either 1 or 2. In the formula for
is either 1 or 2. In the formula for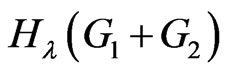 , we partition the set of pairs of vertices of
, we partition the set of pairs of vertices of 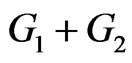 into three subsets
into three subsets 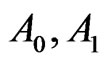 and
and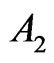 . In
. In 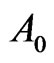 we collect all pairs of vertices u and v such that u is in
we collect all pairs of vertices u and v such that u is in 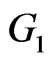 and v is in
and v is in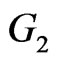 . Hence, they are adjacent in
. Hence, they are adjacent in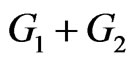 . The set
. The set 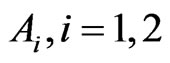 is the set of pairs of vertices u and v which are in
is the set of pairs of vertices u and v which are in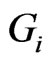 . Also we partition the sum in the formula of
. Also we partition the sum in the formula of 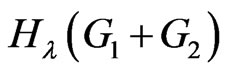 into three sums
into three sums 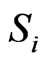 so that
so that  is over
is over 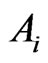 for
for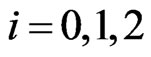 . For
. For 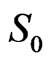 we obtain
we obtain
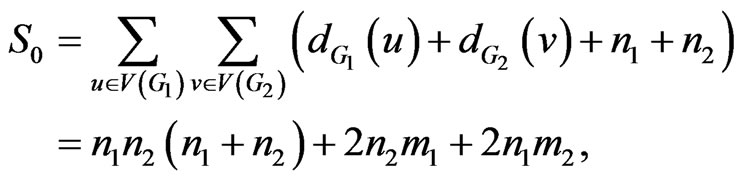
and
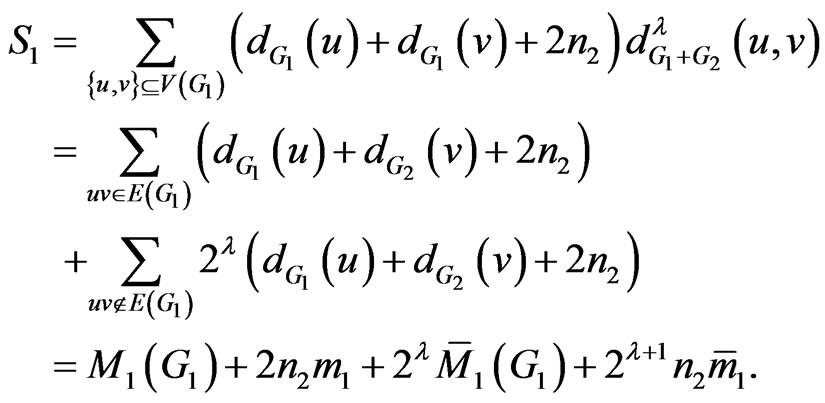
Similarly,
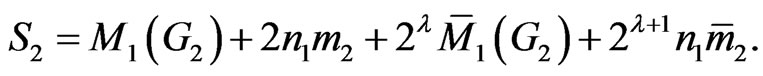
Therefore
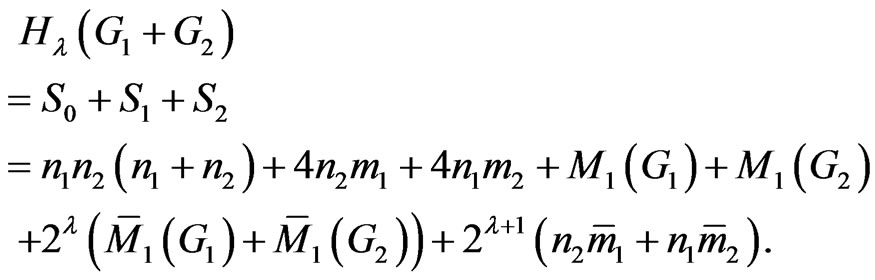 □
□
Corollary 2.3. Let G be a connected graph with n vertices and m edges. Then
 .
.
The exact formulas  for the fan graph K1 + Pn and for the wheel graph
for the fan graph K1 + Pn and for the wheel graph 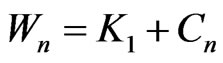 are given in the following Corollary.
are given in the following Corollary.
Corollary 2.4.
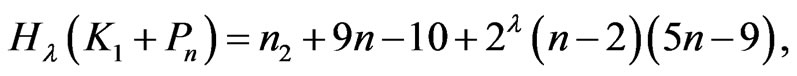
and
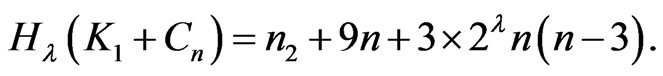
Remark 2.5. In the above theorem, if , then we obtain
, then we obtain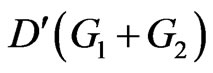 , which gives first derivatives formula Theorem 3 in [22] at
, which gives first derivatives formula Theorem 3 in [22] at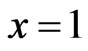 .
.
In the next theorem we obtain the exact formula for the generalized degree distance of the composition of two graphs.
Theorem 2.6. Let 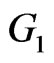 and
and 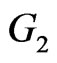 be two graphs. Then
be two graphs. Then
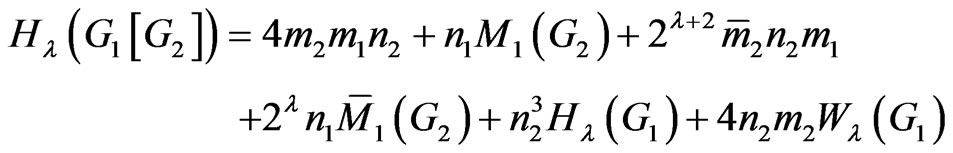
Proof. Suppose 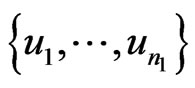 and
and 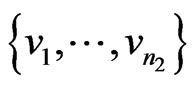 are two set of vertices of
are two set of vertices of 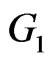 and
and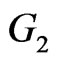 , respectively. Then by Lemma 2.1 and definition of
, respectively. Then by Lemma 2.1 and definition of , we have:
, we have:
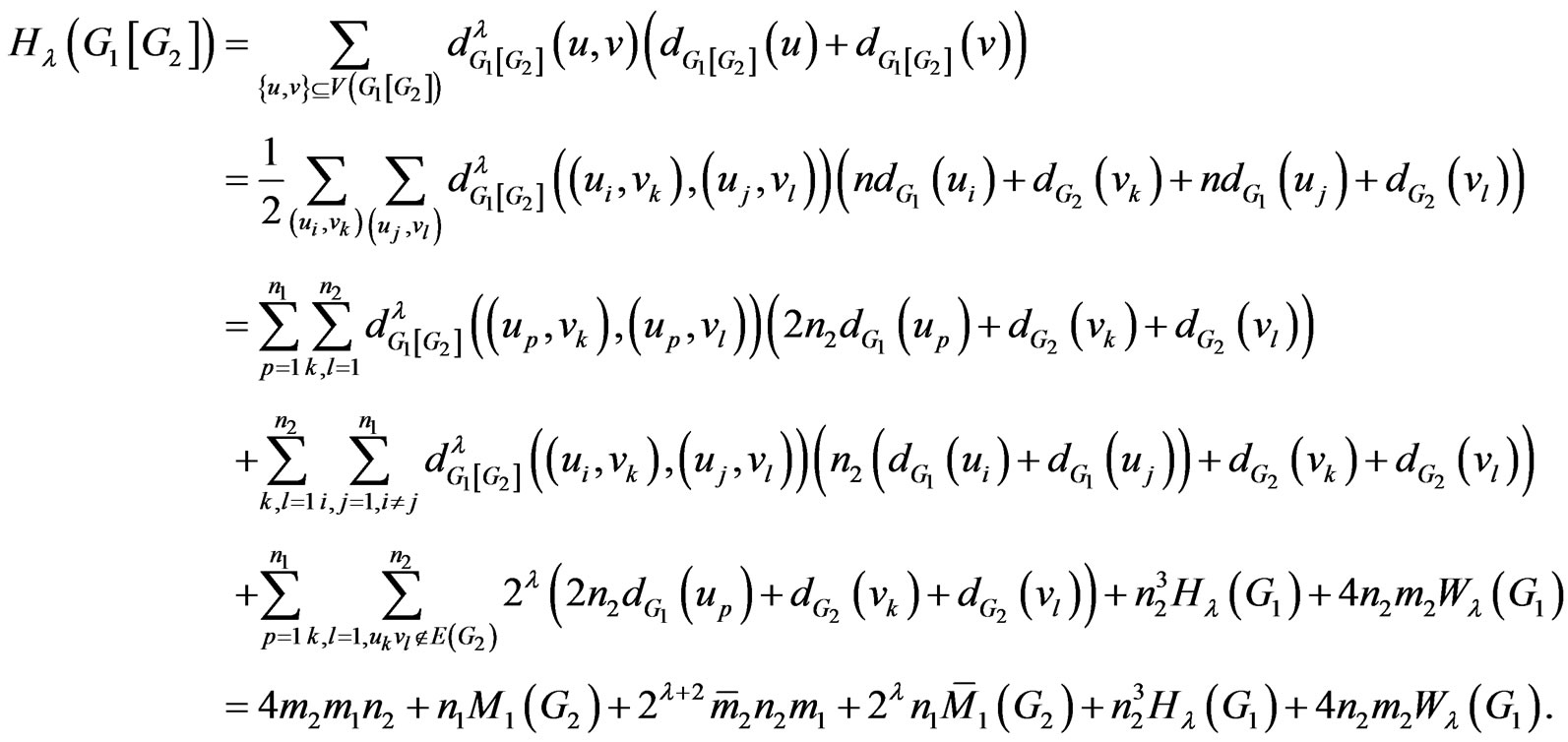
So the proof of theorem is now completed. □
By composing paths and cycles with various small graphs we can obtain classes of polymer-like graphs. Now we give the formula of the 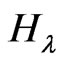 index for the fence graph
index for the fence graph 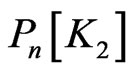 and the closed fence
and the closed fence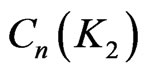 .
.
Corollary 2.7.
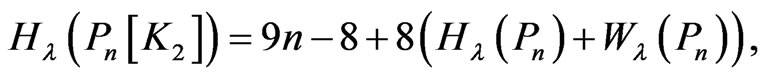
and
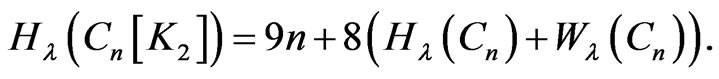
Remark 2.8. In Theorem 2.6, if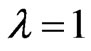 , then we obtain
, then we obtain , which gives first derivatives formula Theorem 5 in [22] at
, which gives first derivatives formula Theorem 5 in [22] at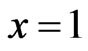 .
.
Now we prove the theorem that characterizes the generalized degree distance of the disjunction of two graphs.
Theorem 2.9. Let 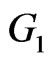 and
and 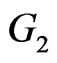 be two graphs. Then
be two graphs. Then
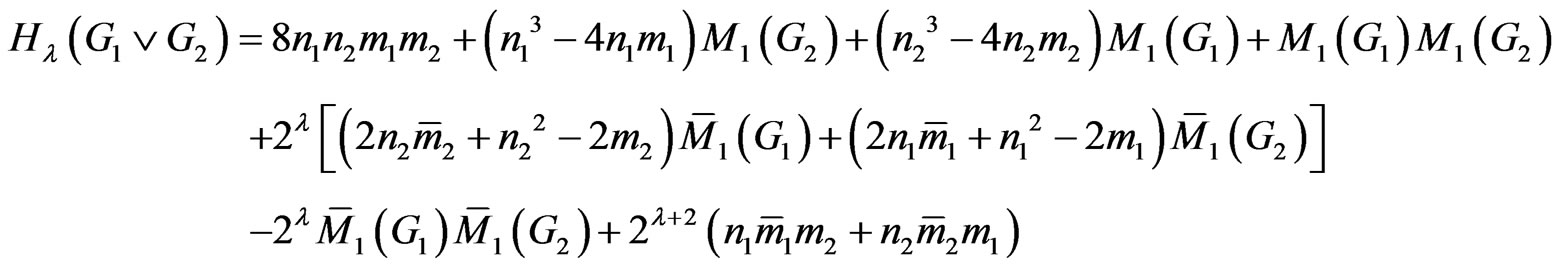
Proof. According to definition of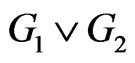 , we have the following relations:
, we have the following relations:
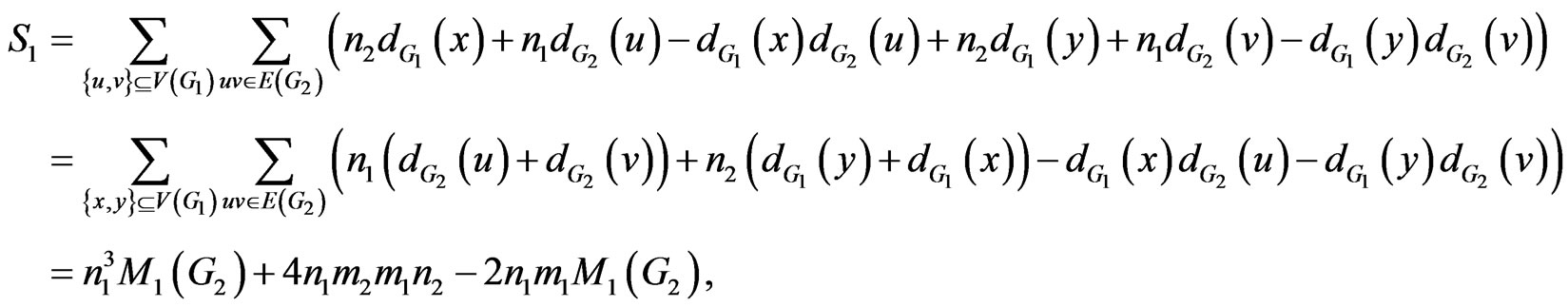
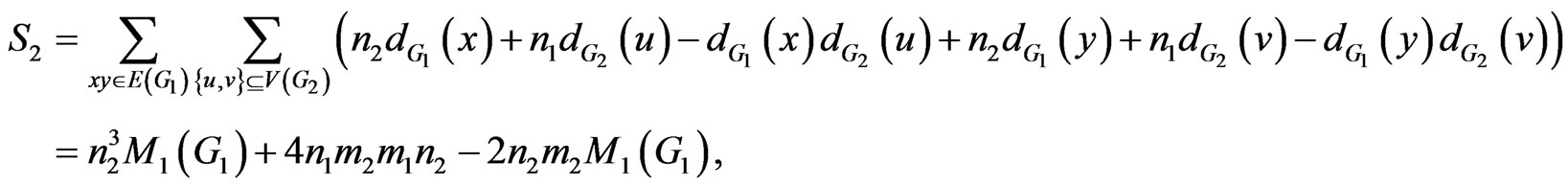
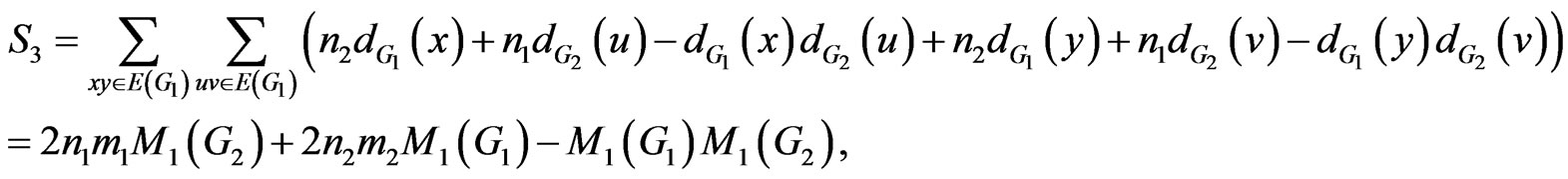
and
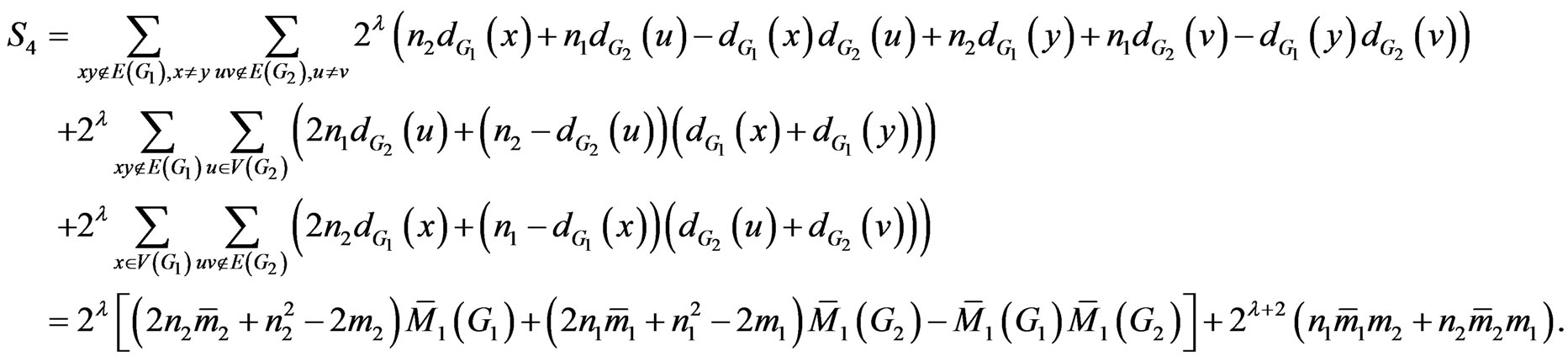
So we have:
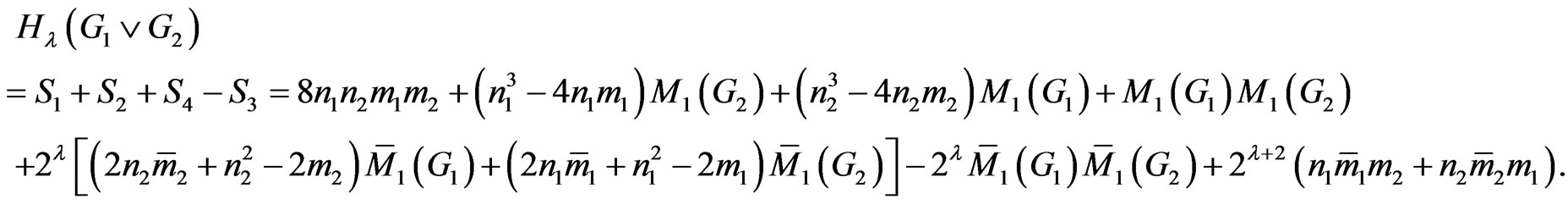
This completes the proof. □
Now we prove the theorem that characterizes the generalized degree distance of the symmetric difference of two graphs.
Theorem 2.10. Let G1 and G2 be two graphs. Then
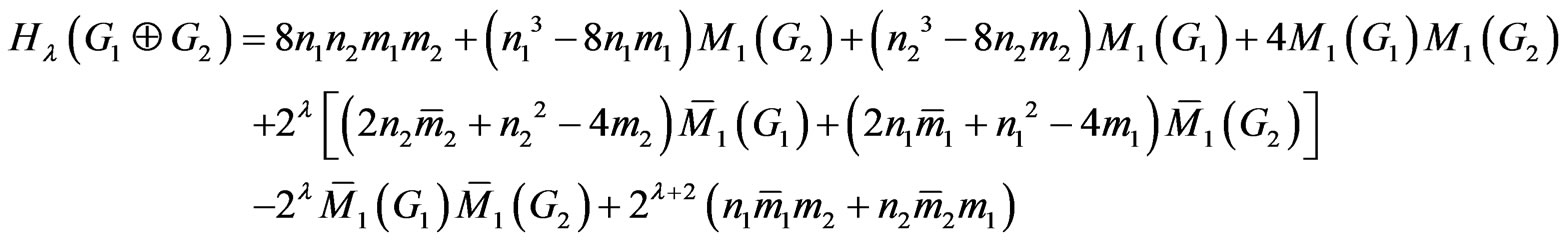
Proof. We consider four sums 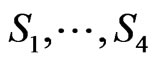 as follows:
as follows:
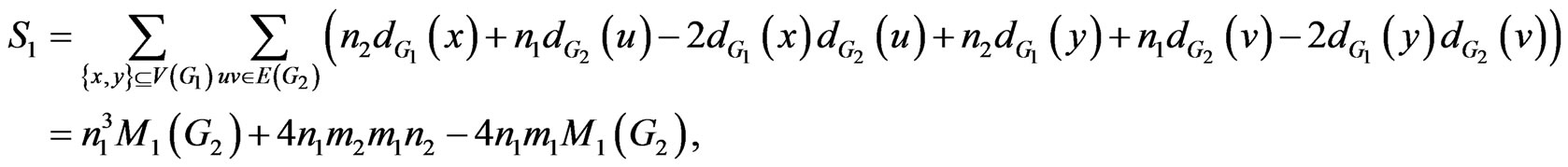
similarly to 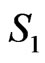
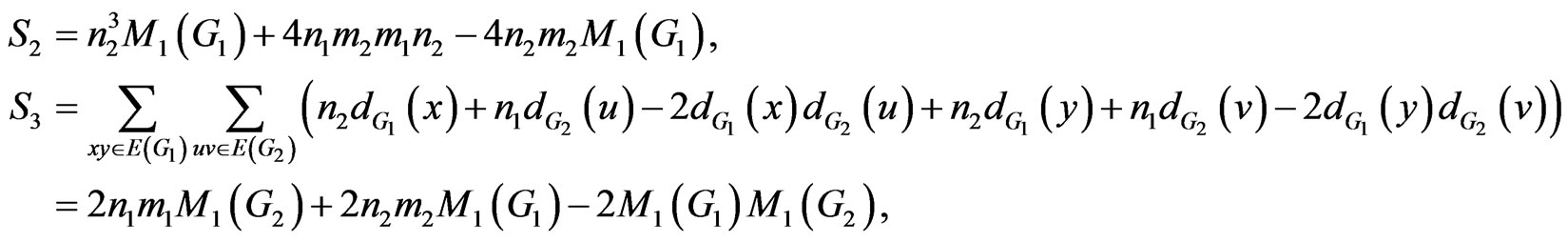
and
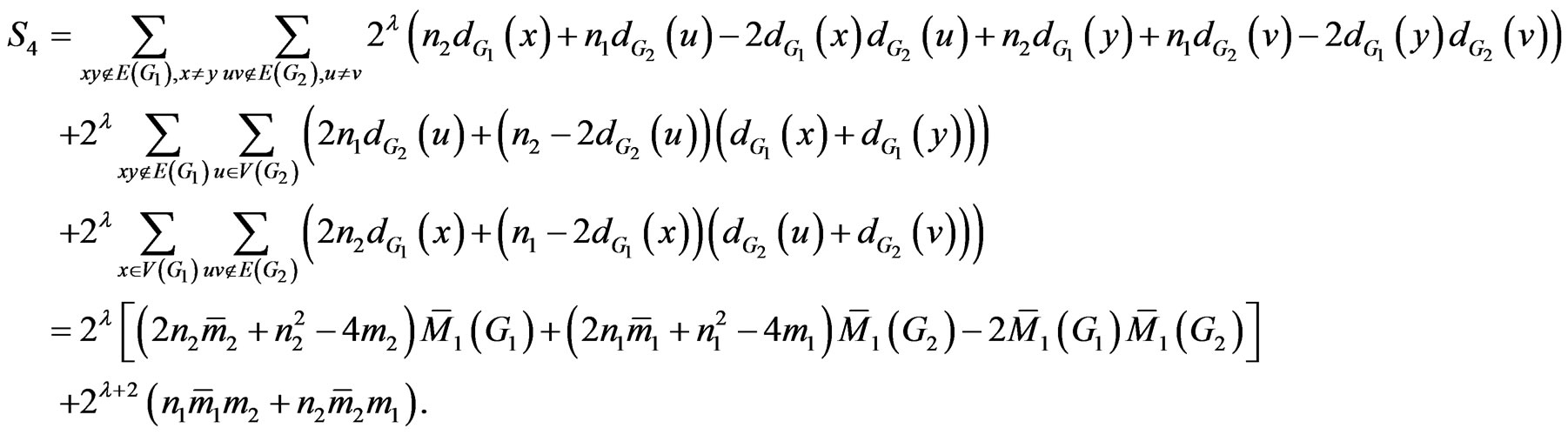
By the definition of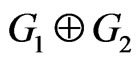 , we have:
, we have:
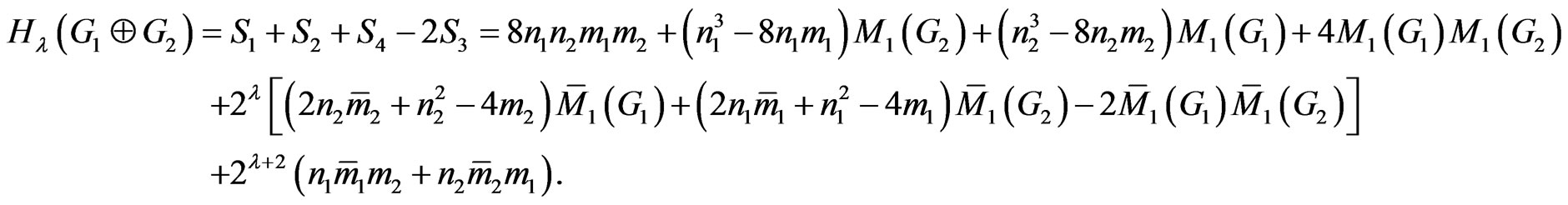
So the proof is now completed. □
In the next theorem we find the generalized degree distance of the Cartesian product of two graphs.
Theorem 2.11. Let 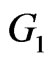 and
and 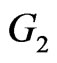 be two graphs. Then
be two graphs. Then
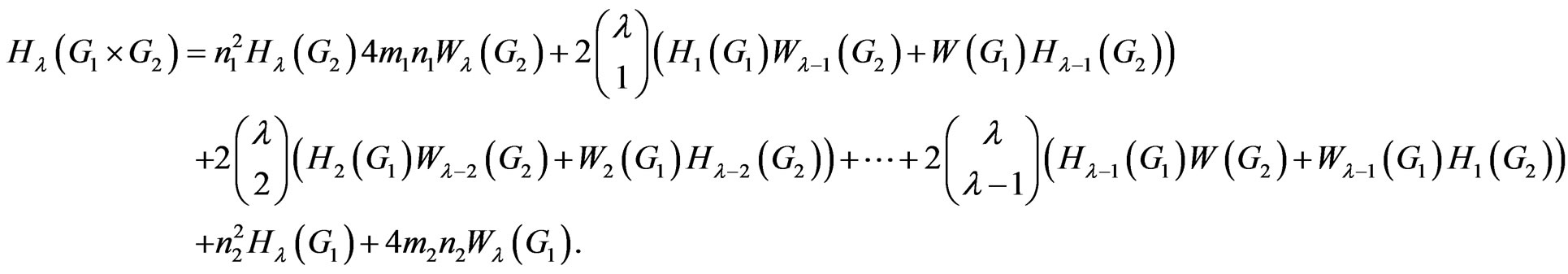
Proof. Suppose 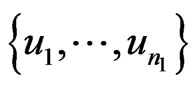 and
and 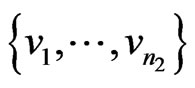 are two set of vertices of
are two set of vertices of  and
and , respectively. Then by Lemma 2.1 and definition of
, respectively. Then by Lemma 2.1 and definition of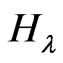 , we have:
, we have:
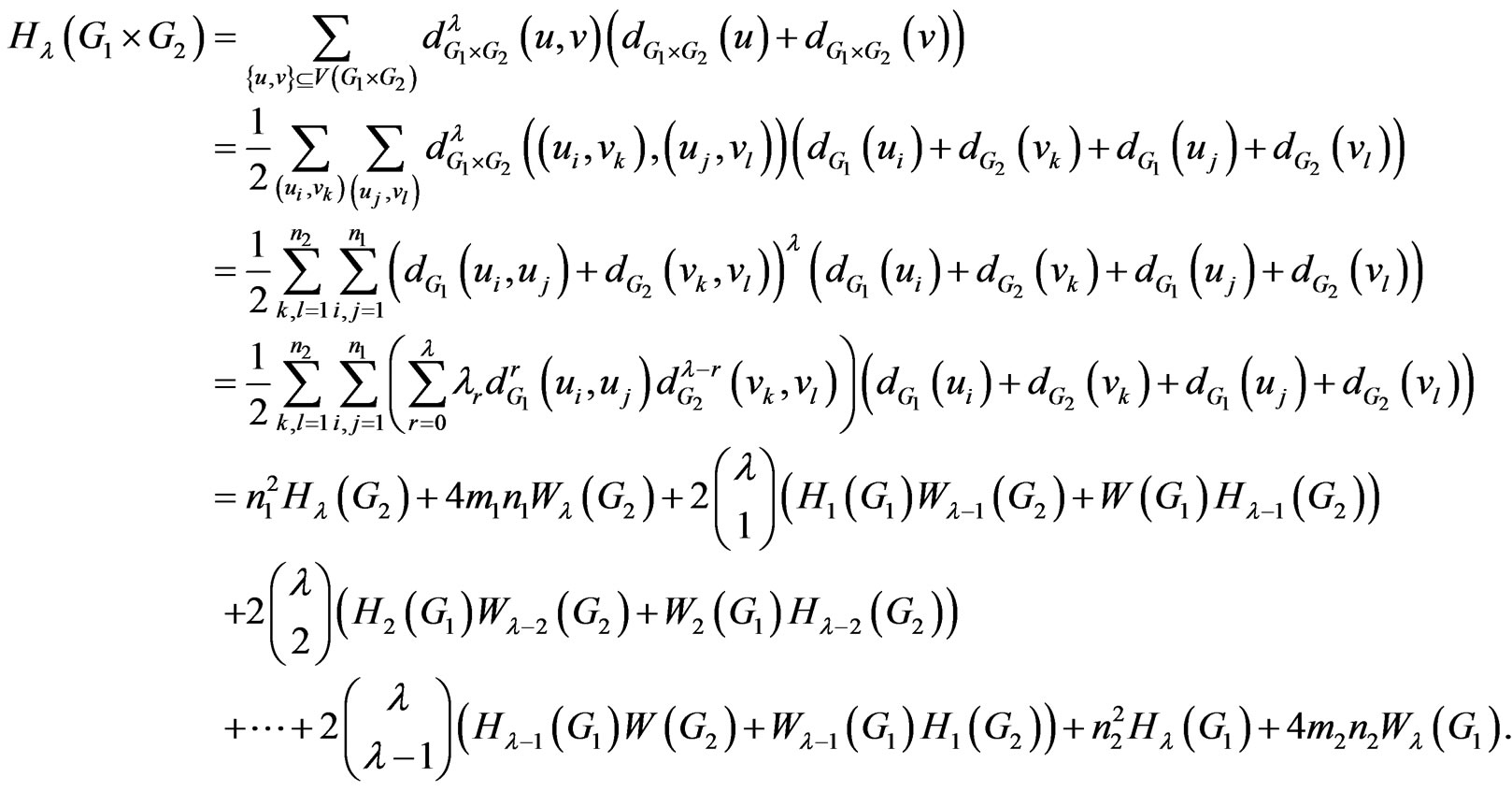
So the proof is now completed. □
As an application of the above theorem, we list explicit formulae for the generalized degree distance of 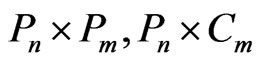 and
and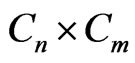 . These graphs are known as the rectangular grid, the
. These graphs are known as the rectangular grid, the 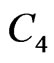 nanotube, and the
nanotube, and the 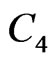 nanotorus, respectively.
nanotorus, respectively.
Lemma 2.12. Define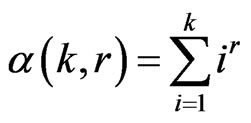 . By [1,23], we have:
. By [1,23], we have:
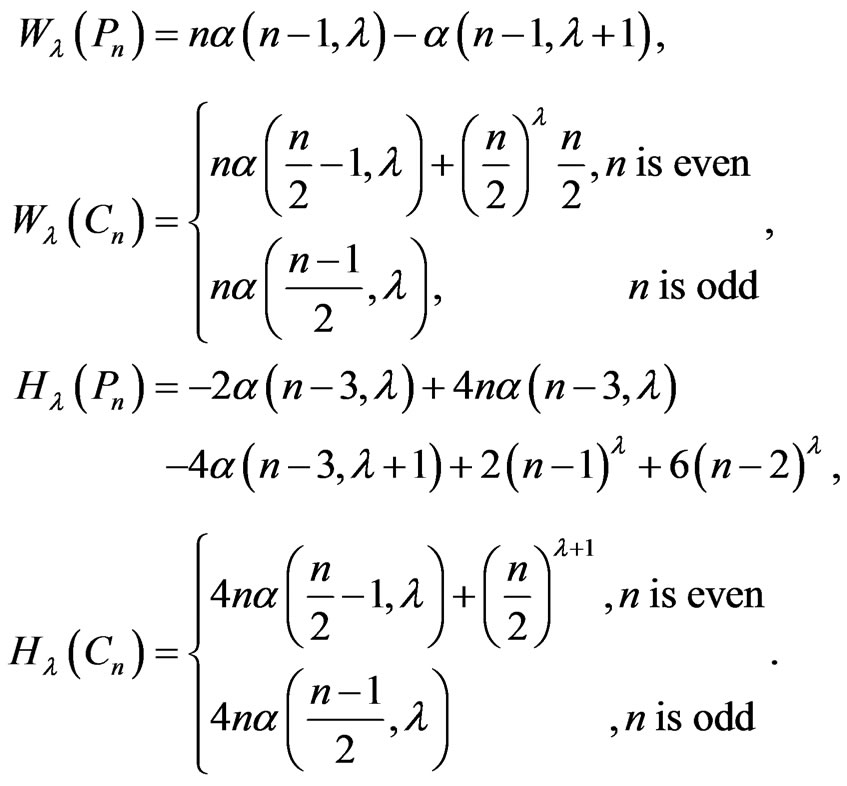
Corollary 2.13. By Theorem 2.9 and Lemma 2.12 we have:
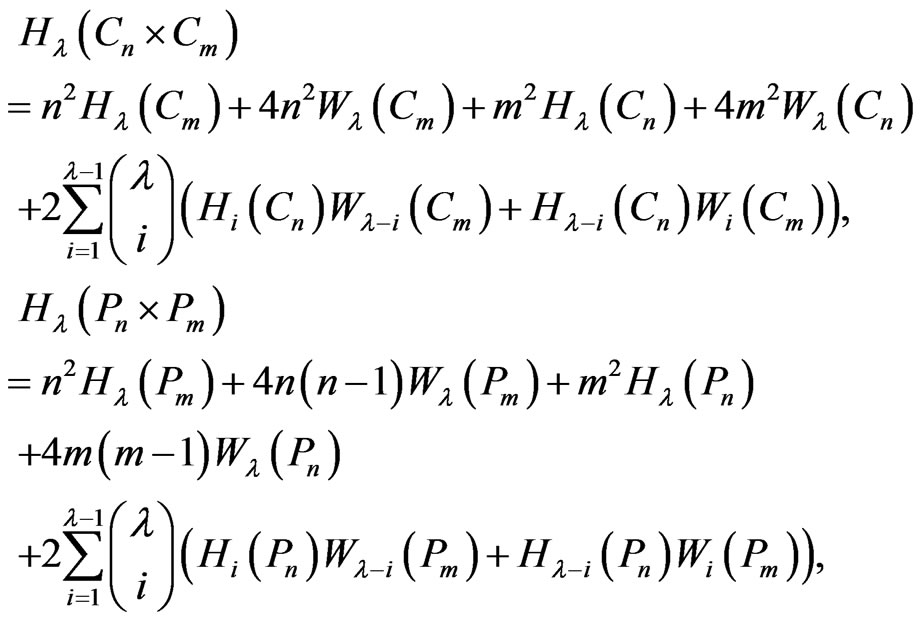
and
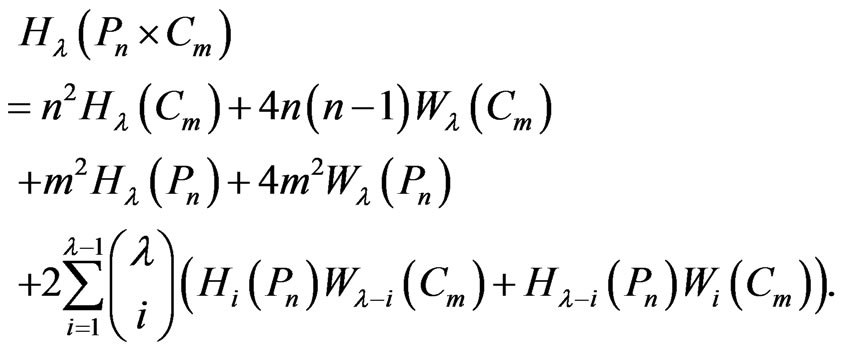
Remark 2.14. In the above theorem, if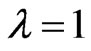 , then we obtain
, then we obtain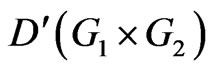 , which gives first derivatives formula Theorem 1 in [22] at
, which gives first derivatives formula Theorem 1 in [22] at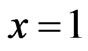 .
.
Now we obtain the relation between the generalized degree distance polynomial and Wiener-type invariant polynomial and the relation between the modified generalized degree distance polynomial and Wiener-type invariant polynomial for graphs.
Theorem 2.15. If 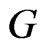 is a graph with
is a graph with 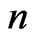 vertices and
vertices and 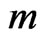 edges, then
edges, then
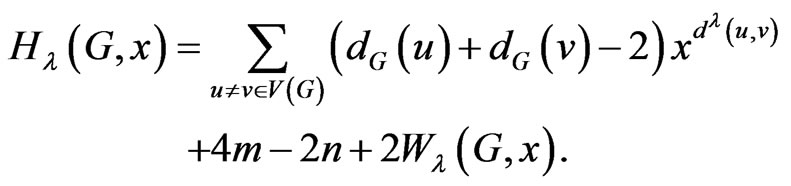
Proof. By definition, we have
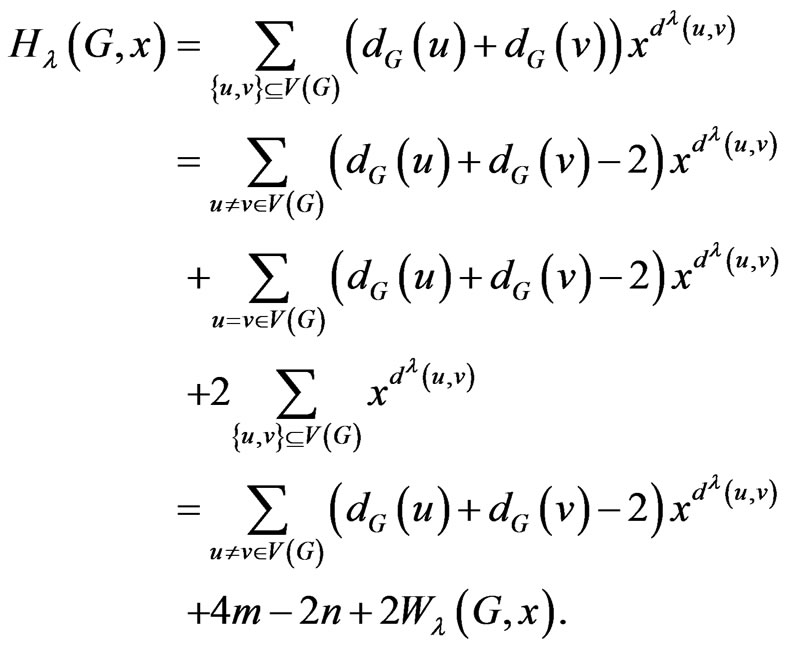
This completes the proof. □
Theorem 2.16. If 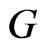 is a graph with
is a graph with 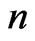 vertices and
vertices and  edges, then
edges, then
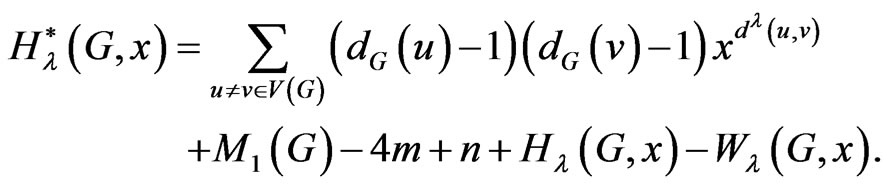
Proof. By definition, we have
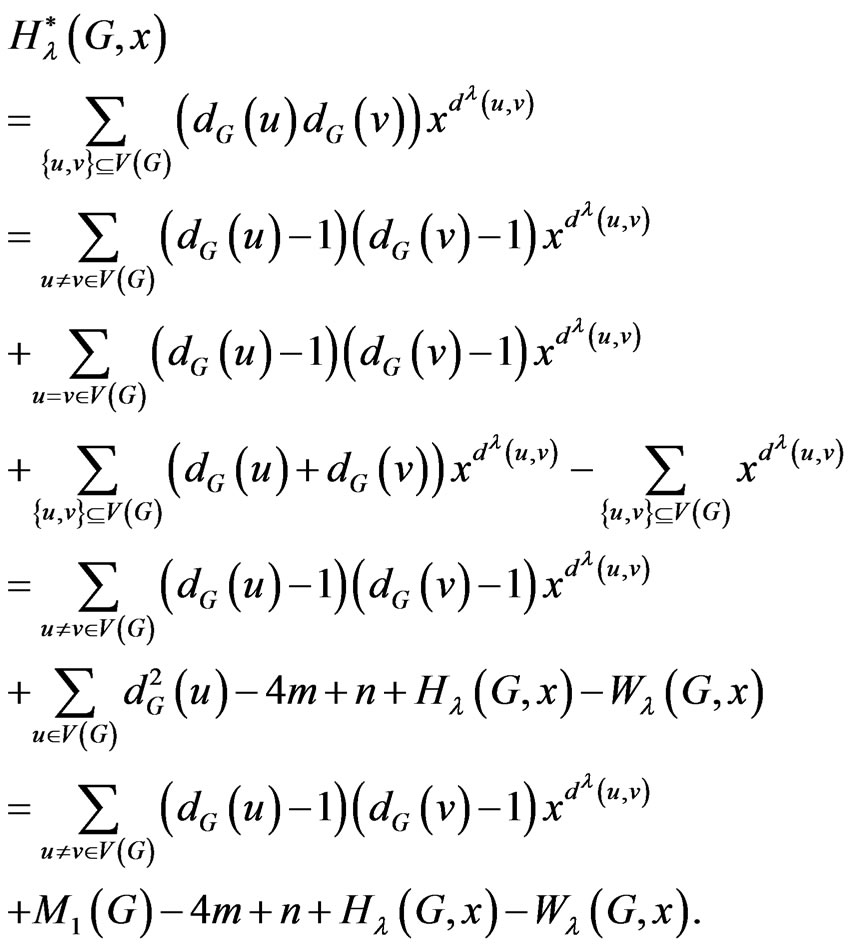
This completes the proof. □
REFERENCES
- A. Hamzeh, A. Iranmanesh, S. Hossein-Zadeh and M. V. Diudea, “Generalized Degree Distance of Trees, Unicyclic and Bicyclic Graphs,” Studia Ubb Chemia, LVII, Vol. 4, 2012, pp. 73-85.
- M. V. Diudea, I. Gutman and L. Jantschi, “Molecular Topology,” Nova Science, Huntington, 2001.
- W. Imrich and S. Klavžar, “Product Graphs: Structure and Recognition,” John Wiley & Sons, New York, 2000.
- I. Gutman and N. Trinajstic, “Graph Theory and Molecular Orbitals. Total π-Electron Energy of Alternant Hydrocarbons,” Chemical Physics Letters, Vol. 17, No. 4, 1972, pp. 535-538. doi:10.1016/0009-2614(72)85099-1
- S. Nikolic, G. Kovacevic, A. Milicevic and N. Trinajstic, “The Zagreb Indices 30 Years after,” Croatica Chemica Acta, Vol. 76, No. 2, 2003, pp. 113-124.
- T. Došlic, “Vertex-Weighted Wiener Polynomials for Composite Graphs,” Ars Mathematica Contemporanea, Vol. 1, No. 1, 2008, pp. 66-80.
- I. Gutman, “A Property of the Wiener Number and Its Modifications,” Indian Journal of Chemistry, Vol. 36A, No. 2, 1997, pp. 128-132.
- I. Gutman, A. A. Dobrynin, S. Klavžar and L. Pavlovic, “Wiener-Type Invariants of Trees and Their Relation,” Bulletin of the Institute of Combinatorics and Its Applications, Vol. 40, No. 1, 2004, pp. 23-30.
- Y. Alizadeh, A. Iranmanesh and T. Došlic, “Additively Weighted Harary Index of Some Composite Graphs,” Discrete Mathematics, Vol. 313, No. 1, 2013, pp. 26-34. doi:10.1016/j.disc.2012.09.011
- A. A. Dobrynin and A. A. Kochetova, “Degree Distance of a Graph: A Degree Analogue of the Wiener Index,” Journal of Chemical Information and Computer Sciences, Vol. 34, No. 5, 1994, pp. 1082-1086. doi:10.1021/ci00021a008
- I. Gutman, “Selected Properties of the Schultz Molecular Topological Index,” Journal of Chemical Information and Computer Sciences, Vol. 34, No. 5, 1994, pp. 1087-1089. doi:10.1021/ci00021a009
- I. Gutman, and S. Klavžar, “Wiener Number of VertexWeighted Graphs and a Chemical Applications,” Discrete Applied Mathematics, Vol. 80, No. 1, 1997, pp. 73-81. doi:10.1016/S0166-218X(97)00070-X
- H. Hua and S. Zhang, “On the Reciprocal Degree Distance of Graphs,” Discrete Applied Mathematics, Vol. 160, No. 7-8, 2012, pp. 1152-1163. doi:10.1016/j.dam.2011.11.032
- S. Hossein-Zadeh, A. Hamzeh and A. R. Ashrafi, “Extremal Properties of Zagreb Coindices and Degree Distance of Graphs,” Miskolc Mathematical Notes, Vol. 11, No. 2, 2010, pp. 129-137.
- I. Tomescu, “Unicyclic and Bicyclic Graphs Having Minimum Degree Distance,” Discrete Applied Mathematics, Vol. 156, No. 1, 2008, pp. 125-130. doi:10.1016/j.dam.2007.09.010
- I. Tomescu, “Some Extremal Properties of the Degree Distance of a Graph,” Discrete Applied Mathematics, Vol. 98, No. 1-2, 1999, pp. 159-163. doi:10.1016/S0166-218X(99)00117-1
- A. Graovac and T. Pisanski, “On the Wiener Index of a Graph,” Journal of Mathematical Chemistry, Vol. 8, No. 1, 1991, pp. 53-62. doi:10.1007/BF01166923
- B. E. Sagan, Y.-N. Yeh and P. Zhang, “The Wiener Polynomial of a Graph,” International Journal of Quantum Chemistry, Vol. 60, No. 5, 1996, pp. 959-969. doi:10.1002/(SICI)1097-461X(1996)60:5<959::AID-QUA2>3.0.CO;2-W
- S. Klavžar, A. Rajapakse and I. Gutman, “The Szeged and the Wiener Index of Graphs,” Applied Mathematics Letters, Vol. 9, No. 5, 1996, pp. 45-49. doi:10.1016/0893-9659(96)00071-7
- M. H. Khalifeh, H. Yousefi-Azari and A. R. Ashrafi, “The Hyper-Wiener Index of Graph Operations,” Computers & Mathematics with Applications, Vol. 56, No. 5, 2008, pp. 1402-1407. doi:10.1016/j.camwa.2008.03.003
- M. Eliasi and A. Iranmanesh, “The Hyper-Wiener Index of the Generalized Hierarchical Product of Graphs,” Discrete Applied Mathematics, Vol. 159, No. 8, 2011, pp. 866-871. doi:10.1016/j.dam.2010.12.020
- M. Eliasi and B. Taeri, “Schultz Polynomials of Composite Graphs,” Applicable Analysis and Discrete Mathematics, Vol. 2, No. 2, 2008, pp. 285-296. doi:10.2298/AADM0802285E
- S. Hossein-Zadeh, A. Hamzeh and A. R. Ashrafi, “WienerType Invariants of Some Graph Operations,” Filomat, Vol. 29, No. 3, 2009, pp. 103-113. doi:10.2298/FIL0903103H
- M. H. Khalifeh, H. Yousefi-Azari and A. R. Ashrafi, “The First and Second Zagreb Indices of Some Graph Operations,” Discrete Applied Mathematics, Vol. 157, No. 4, 2009, pp. 804-811. doi:10.1016/j.dam.2008.06.015
- F. Harary, “Graph Theory,” Addison-Wesley, Reading, 1969.
- N. Trinajstic, “Chemical Graph Theory,” CRC Press, Boca Raton, 1992.
NOTES
*Corresponding author.

