Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27380,6 pages DOI:10.4236/ojdm.2013.31007
Characterization and Construction of Permutation Graphs
1Department of Mathematics, De La Salle University, Manila, Philippines
2Department of Mathematics and Computer Science, University of the Philippines, Baguio City, Philippines
Email: severino.gervacio@dlsu.edu.ph
Received September 15, 2012; revised October 15, 2012; accepted October 25, 2012
Keywords: Permutation; Inversion; Permutation Graph; Cohesive Order; Oriented Graph; Tournament Score Sequence; Caterpillar; Graph Composition
ABSTRACT
If  is a permutation of
is a permutation of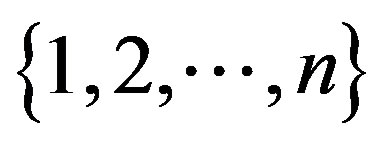 , the graph
, the graph 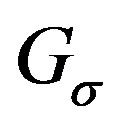 has vertices
has vertices  where
where 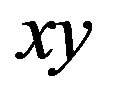 is an edge of
is an edge of  if and only if
if and only if  or
or 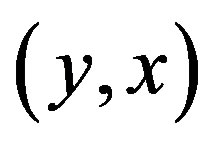 is an inversion of
is an inversion of . Any graph isomorphic to
. Any graph isomorphic to 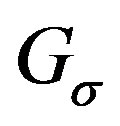 is called a permutation graph. In 1967 Gallai characterized permutation graphs in terms of forbidden induced subgraphs. In 1971 Pnueli, Lempel, and Even showed that a graph is a permutation graph if and only if both the graph and its complement have transitive orientations. In 2010 Limouzy characterized permutation graphs in terms of forbidden Seidel minors. In this paper, we characterize permutation graphs in terms of a cohesive order of its vertices. We show that only the caterpillars are permutation graphs among the trees. A simple method of constructing permutation graphs is also presented here.
is called a permutation graph. In 1967 Gallai characterized permutation graphs in terms of forbidden induced subgraphs. In 1971 Pnueli, Lempel, and Even showed that a graph is a permutation graph if and only if both the graph and its complement have transitive orientations. In 2010 Limouzy characterized permutation graphs in terms of forbidden Seidel minors. In this paper, we characterize permutation graphs in terms of a cohesive order of its vertices. We show that only the caterpillars are permutation graphs among the trees. A simple method of constructing permutation graphs is also presented here.
1. Introduction
A bijection  of
of  to itself is called a permutation of order
to itself is called a permutation of order . We shall write
. We shall write 
to mean that  for
for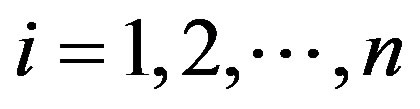 . We shall denote by
. We shall denote by  the set of all permutations of
the set of all permutations of .
.
An inversion of  is an ordered pair
is an ordered pair 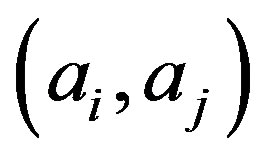 where
where
 but
but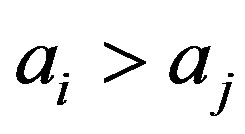 . Equivalently,
. Equivalently, 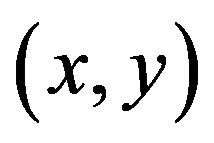 is an inversion if and only if
is an inversion if and only if  and
and .
.
Definition 1.1 Let . The graph of inversions of
. The graph of inversions of , denoted by
, denoted by , is the graph with vertices
, is the graph with vertices  where
where 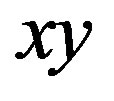 is an edge of
is an edge of 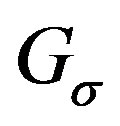 if and only if
if and only if 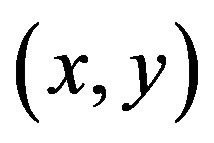 or
or 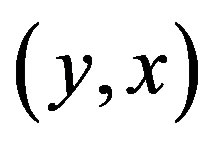 is an inversion of
is an inversion of .
.
The term graph of inversions was used by Ramos in [1]. For our purpose in this paper, any graph isomorphic to 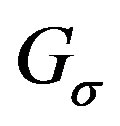 for some permutation
for some permutation  will be called a permutation graph. There is an implementation PermutationGraph[p] in the Combinatorica package of Mathematica [2] that creates the permutation graph
will be called a permutation graph. There is an implementation PermutationGraph[p] in the Combinatorica package of Mathematica [2] that creates the permutation graph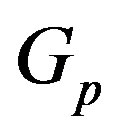 .
.
In 1967 Gallai [3] characterized permutation graphs in terms of forbidden induced subgraphs. In 1971 Pnueli, Lempel, and Even [4] showed that a graph 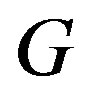 is a permutation graph if and only if both
is a permutation graph if and only if both 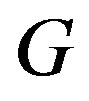 and its complement
and its complement  have transitive orientations. Recently in 2010 Limouzy [5] gave a characterization of permutation graphs in terms of forbidden Seidel minors.
have transitive orientations. Recently in 2010 Limouzy [5] gave a characterization of permutation graphs in terms of forbidden Seidel minors.
A characterization of permutation graphs in terms of cohesive vertex-set order is established in this paper. We prove that the only permutation graphs among the trees are the caterpillars. In addition, we describe a simple method of constructing permutation graphs.
2. Cohesive Vertex-Set Order
The vertex-set of a graph  will be denoted by
will be denoted by  while the edge-set will be denoted by
while the edge-set will be denoted by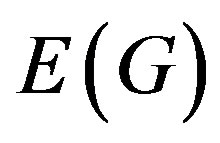 . An edge with end-vertices
. An edge with end-vertices  and
and 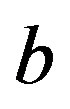 will be denoted by
will be denoted by 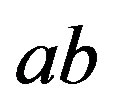 or
or . For graph theoretic terms used here without definition, the book by Harary [6] may be referred to.
. For graph theoretic terms used here without definition, the book by Harary [6] may be referred to.
Consider the permutation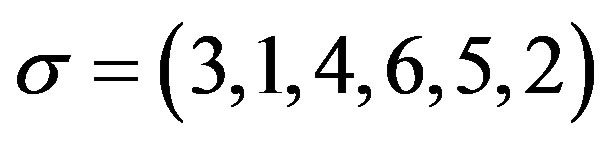 . The inversions of
. The inversions of  are
are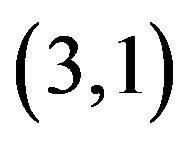 ,
,  ,
,  ,
,  ,
, 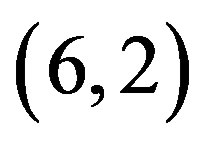 , and
, and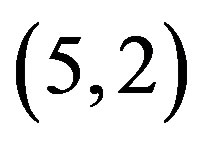 . It is convenient to draw the graph
. It is convenient to draw the graph 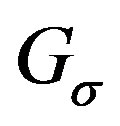 with the vertices in a line following their arrangement in
with the vertices in a line following their arrangement in . A drawing of
. A drawing of 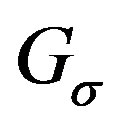 is shown in Figure 1.
is shown in Figure 1.
There are some important properties of the drawing that we need to take note of.
(a) If 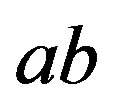 and
and 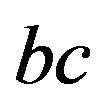 are two edges of the graph where
are two edges of the graph where  lies between
lies between  and
and  in the drawing, then
in the drawing, then  is also an edge.
is also an edge.

Figure 1. Permutation graph ,
,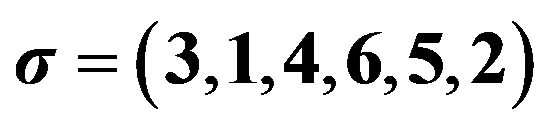 .
.
(b) If  is an edge and
is an edge and  is a vertex that lies between
is a vertex that lies between 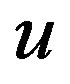 and
and 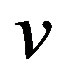 in the drawing, then either
in the drawing, then either 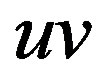 is an edge or
is an edge or  is an edge.
is an edge.
We define more precisely the properties that we observed.
Definition 2.1 Let  be a graph of order
be a graph of order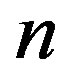 . An arrangement
. An arrangement  of the vertices of
of the vertices of 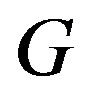 is called a cohesive vertex-set order of
is called a cohesive vertex-set order of  (or simply cohesive order
(or simply cohesive order ) if the following conditions are satisfied:
) if the following conditions are satisfied:
(a) If  and
and ,
, 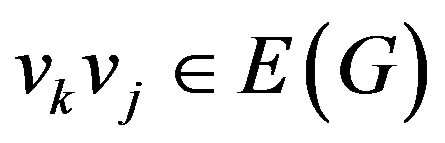 , then
, then 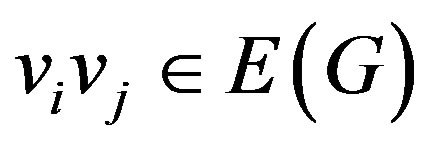 .
.
(b) If 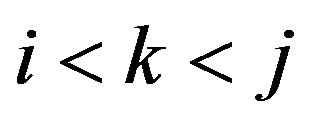 and
and , then
, then 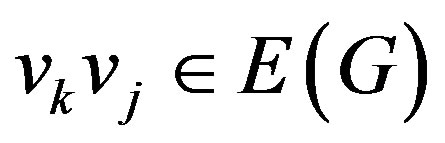 or
or .
.
The complement of a graph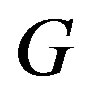 , denoted by
, denoted by 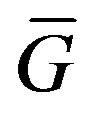 has the same vertex-set as
has the same vertex-set as  and two distinct vertices
and two distinct vertices  and
and  form the edge
form the edge  in
in 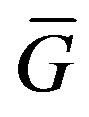 if and only if
if and only if  is not an edge in
is not an edge in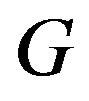 .
.
Lemma 2.1 Let 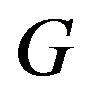 be a graph. Then
be a graph. Then  is a cohesive order of
is a cohesive order of 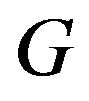 if and only if
if and only if  is a cohesive order of
is a cohesive order of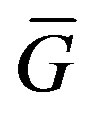 .
.
Proof. Let  be a cohesive order of
be a cohesive order of . We claim that the same is a cohesive order of
. We claim that the same is a cohesive order of . To prove
. To prove  for
for , let
, let  and
and  be vertices of
be vertices of 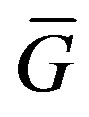 such that
such that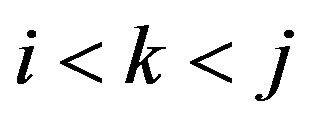 . Then
. Then 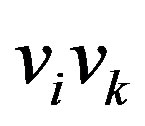 and
and 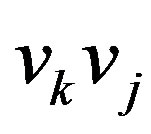 are not edges in
are not edges in . By property
. By property  of a cohesive order, the edge
of a cohesive order, the edge 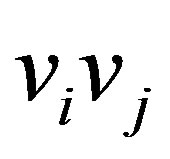 is not in
is not in . Hence,
. Hence, 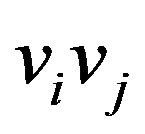 is an edge of
is an edge of . To prove
. To prove  for
for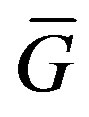 , let
, let  be an edge of
be an edge of 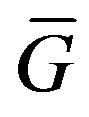 with
with . Let
. Let  be an integer such that
be an integer such that . Since
. Since 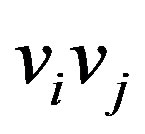 is in
is in , then it is not in
, then it is not in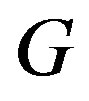 . By property
. By property  of a cohesive order (for
of a cohesive order (for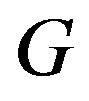 ) the edges
) the edges 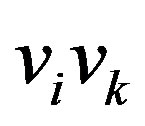 and
and 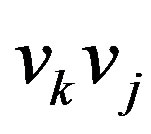 cannot be both in
cannot be both in . Hence at least one of them is in
. Hence at least one of them is in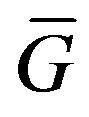 .
.
The converse follows since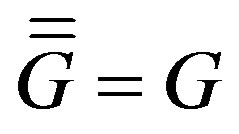 .
.
The next result follows easily from the definition of permutation graph and cohesive order. We shall omit the proof of this theorem.
Theorem 2.1 Let . Then
. Then
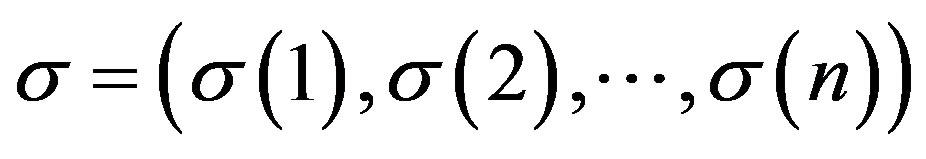
is a cohesive order of the permutation graph .
.
Note that  is a cohesive order of a graph
is a cohesive order of a graph  if and only if
if and only if  is a cohesive order of
is a cohesive order of .
.
To assign a direction to an edge  of a graph
of a graph  means to change
means to change  to either the ordered pair
to either the ordered pair  or the ordered pair
or the ordered pair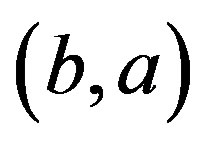 .
.
Definition 2.2 An orientation of a graph  is the digraph obtained by assigning a direction to each edge of
is the digraph obtained by assigning a direction to each edge of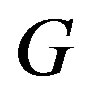 . The directed edges, which are ordered pairs, are called arcs.
. The directed edges, which are ordered pairs, are called arcs.
A digraph  is said to be transitive if
is said to be transitive if  is an arc of
is an arc of  whenever
whenever 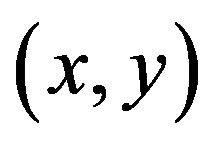 and
and  are arcs in
are arcs in .
.
In a digraph , the out-degree of a vertex
, the out-degree of a vertex , denoted by
, denoted by  or simply
or simply 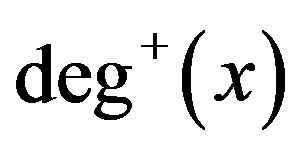 is the numnber of vertices
is the numnber of vertices  in
in  such that
such that  is an arc in
is an arc in . The in-degree of
. The in-degree of , denoted by
, denoted by  or
or  is the number of vertices
is the number of vertices 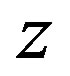 in
in  such that
such that 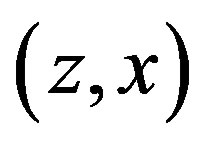 is an arc in
is an arc in .
.
An oriented complete graph is called a tournament [7]. The score of a vertex  in a tournament, denoted by
in a tournament, denoted by  is defined by
is defined by . The score sequence of a tournament is the sequence of scores arranged in non-decreasing order.
. The score sequence of a tournament is the sequence of scores arranged in non-decreasing order.
The following theorem [8] is not difficult, and is stated without proof.
Theorem 2.2 Let 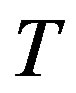 be a tournament of order
be a tournament of order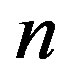 . The following statements are equivalent:
. The following statements are equivalent:
1)  is transitive.
is transitive.
2) For all vertices  and
and 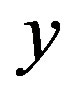 in
in , if
, if 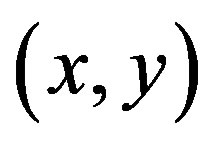 is an arc of
is an arc of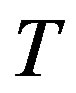 , then
, then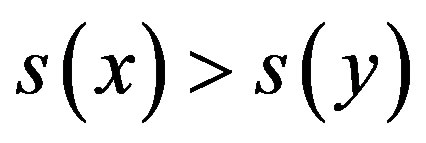 .
.
3) For all vertices  and
and  in
in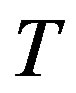 , if
, if , then
, then 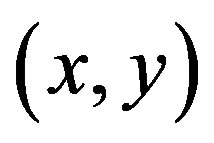 is an arc of
is an arc of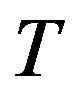 .
.
4) The score sequence of 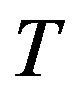 is
is .
.
Our main result, which characterizes permutation graphs, is the following theorem.
Theorem 2.3 A graph  is a permutation graph if and only if it has a cohesive order.
is a permutation graph if and only if it has a cohesive order.
Proof. If  is a permutation graph, then
is a permutation graph, then 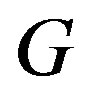 is isomorphic to
is isomorphic to  for some permutation
for some permutation . By Theorem 2.1,
. By Theorem 2.1,  is a a cohesive order of
is a a cohesive order of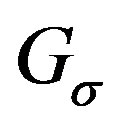 . Let
. Let 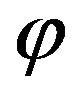 be an isomorphism of
be an isomorphism of 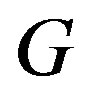 to
to . Then
. Then 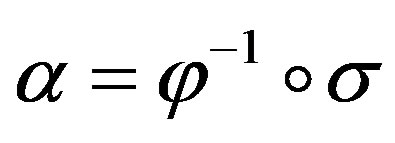 is a cohesive order of
is a cohesive order of .
.
Conversely, let  be a graph with a cohesive order
be a graph with a cohesive order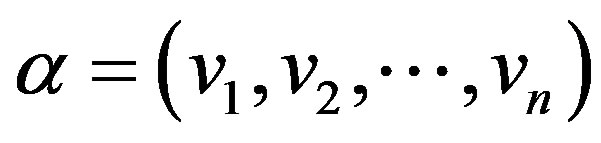 . Orient
. Orient  to obtain a digraph
to obtain a digraph  as follows: For each edge
as follows: For each edge 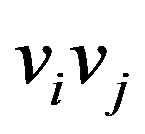 in
in , assign the direction
, assign the direction  if
if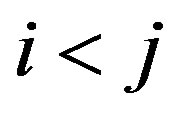 ; otherwise assign the direction
; otherwise assign the direction
 .
.
By property 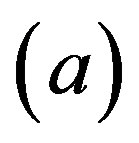 of a cohesive order, it follows that
of a cohesive order, it follows that  is transitive. Extend
is transitive. Extend  to a tournament by orienting the complement
to a tournament by orienting the complement  of
of  as follows: If
as follows: If 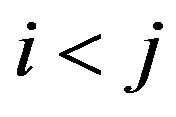 but
but 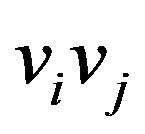 is not in
is not in , assign the direction
, assign the direction  to the edge
to the edge 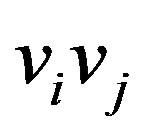 in
in . By Lemma 2.1
. By Lemma 2.1 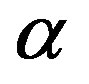 is a cohesive order of
is a cohesive order of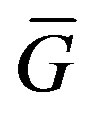 . So likewise, the orientation of
. So likewise, the orientation of 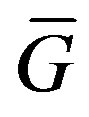 obtained in this manner is also transitive. Let us denote this digraph by
obtained in this manner is also transitive. Let us denote this digraph by .
.
The union of  and
and  is an orientation of
is an orientation of . Since
. Since  is complete, then
is complete, then 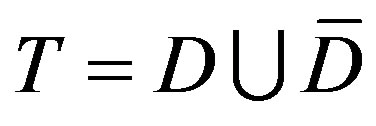 is a tournament. We claim that
is a tournament. We claim that  is a transitive tournament. Let
is a transitive tournament. Let 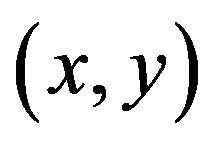 and
and 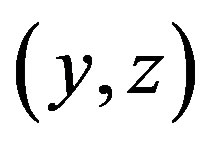 be arcs of
be arcs of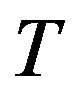 . If both arcs belong to
. If both arcs belong to  or to
or to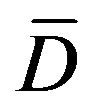 , then
, then  is in
is in 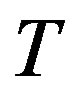 because both
because both  and
and  are transitive. So let us assume that one of the arcs belong to
are transitive. So let us assume that one of the arcs belong to  and the other arc belong to
and the other arc belong to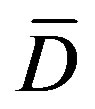 . Without loss of generality, assume that
. Without loss of generality, assume that  is an arc in
is an arc in , and
, and  is an arc in
is an arc in . If
. If 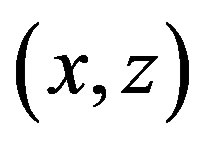 is in
is in , we are done. If
, we are done. If 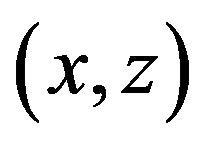 is not in
is not in , then
, then 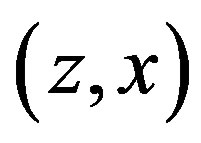 is in
is in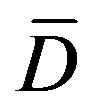 . Since
. Since  is transitive and
is transitive and ,
, 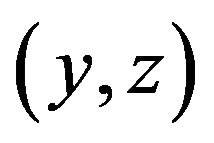 are in
are in , then
, then  is in
is in . This is a contradiction because
. This is a contradiction because  is in
is in .
.
By Theorem 2.2, the score sequence of 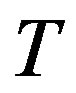 is
is  . Let
. Let  be the permutation defined by
be the permutation defined by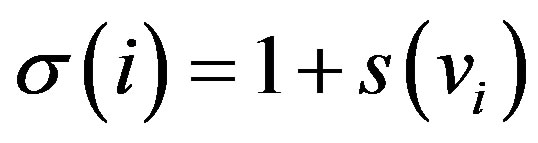 , where
, where 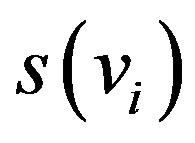 is the score of
is the score of  in
in . We claim that the mapping
. We claim that the mapping 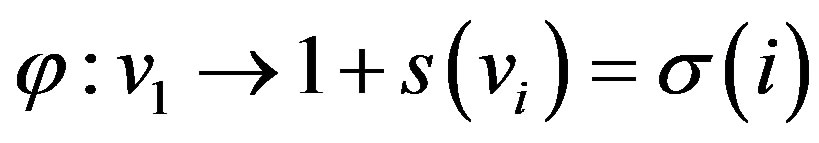 is an isomorphism of
is an isomorphism of 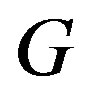 to
to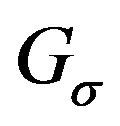 .
.
The mapping 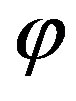 is bijective since the scores of the vertices are distinct. It remains to show that
is bijective since the scores of the vertices are distinct. It remains to show that  preserves adjacency. Let
preserves adjacency. Let 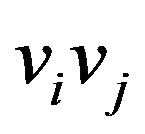 be an edge of
be an edge of , where
, where . In
. In  we have the arc
we have the arc . Since the tournament
. Since the tournament 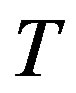 is transitive, then by Theorem 2.2,
is transitive, then by Theorem 2.2,
 . Hence,
. Hence, 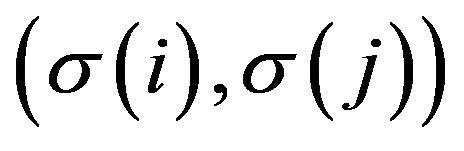 is an inversion of
is an inversion of
 . Therefore,
. Therefore,  and
and  are adjacent in
are adjacent in . Conversely, let
. Conversely, let  be an edge in
be an edge in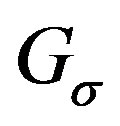 . Then either
. Then either 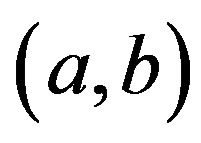 or
or 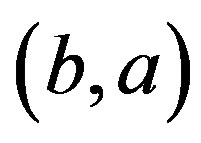 is an inversion. Without loss of generality, assume that
is an inversion. Without loss of generality, assume that 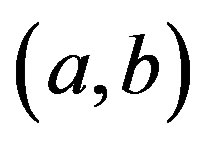 is an inversion. Let
is an inversion. Let  and
and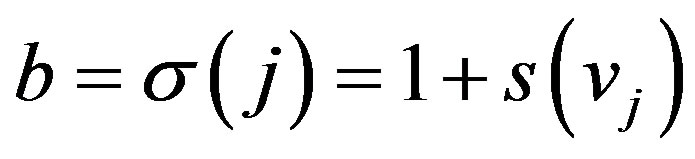 , where
, where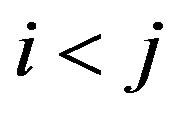 . Since
. Since  is an inversion, we have
is an inversion, we have , or
, or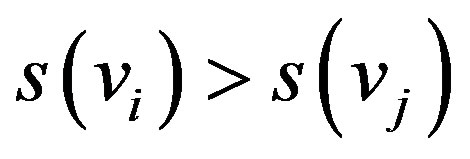 . Therefore, the arc
. Therefore, the arc  is in
is in . Since
. Since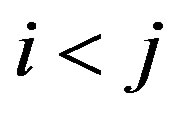 , the arc
, the arc 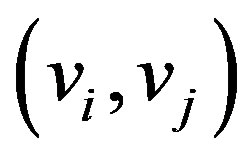 must be in
must be in . Consequently, the edge
. Consequently, the edge  is in
is in .
.
Here is an illustration of the constructive proof of Theorem 2.3. Consider the graph 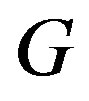 shown in Figure 2 with a cohesive order
shown in Figure 2 with a cohesive order .
.
To be able to follow the discussion in the proof of theorem without difficulty, let
 .
.
Using the bottom drawing in Figure 2, we construct a digraph by directing all edges from left to right. For two vertices not adjacent in , we assign the arc that goes from right to left. Then the result is a transitive tournament. It is not difficult to get the score of any vertex in this tournament. We simply count the eastbound arcs and the westbound arcs with a fixed tail. Consider for example,
, we assign the arc that goes from right to left. Then the result is a transitive tournament. It is not difficult to get the score of any vertex in this tournament. We simply count the eastbound arcs and the westbound arcs with a fixed tail. Consider for example,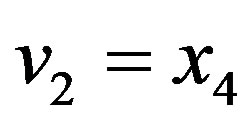 . The number of eastbound arcs with tail at
. The number of eastbound arcs with tail at 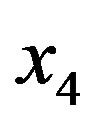 is 3. The number of westbound arcs is simply the number of vertices to its left that are not adjacent to to
is 3. The number of westbound arcs is simply the number of vertices to its left that are not adjacent to to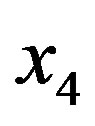 . The table below summarizes the scores of the vertices.
. The table below summarizes the scores of the vertices.
| Vertex | v1 = x2 | v2 = x4 | v3 = x1 | v4 = x3 | v5 = x5 |
| Score, s(vi) | 2 | 4 | 0 | 1 | 3 |
Take the permutation  defined by
defined by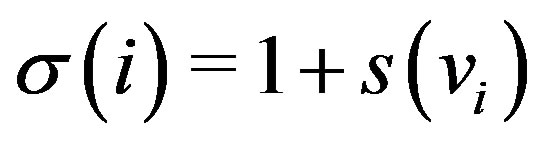 . Then
. Then . The permutation graph
. The permutation graph 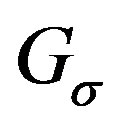 is shown in Figure 3.
is shown in Figure 3.
3. Construction and Examples of Permutation Graphs
Some fundamental facts about permutation graphs are given in the next theorem.
Theorem 3.1 Let 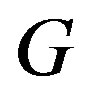 be a graph. The following are equivalent:
be a graph. The following are equivalent:
(a)  is a permutation graph.
is a permutation graph.
(b) 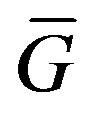 is a permutation graph.
is a permutation graph.

Figure 2. A graph 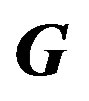 with cohesive order
with cohesive order 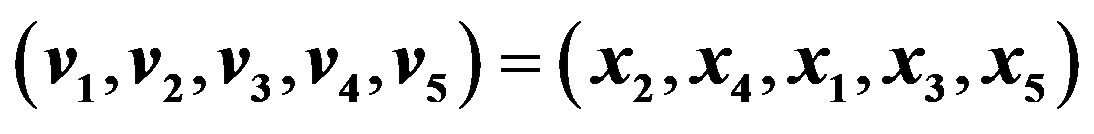 .
.

Figure 3. The permutation graph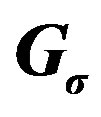 ,
, .
.
(c) Every induced subgraph of 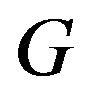 is a permutation graph.
is a permutation graph.
(d) Every connected component of  is a permutation graph.
is a permutation graph.
Proof. From Lemma 2.1, 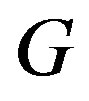 has a cohesive order if and only if
has a cohesive order if and only if 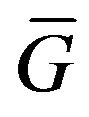 has a cohesive order. Therefore, (a) and (b) are equivalent.
has a cohesive order. Therefore, (a) and (b) are equivalent.
If 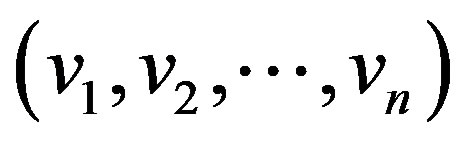 is a cohesive order of
is a cohesive order of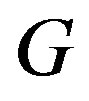 , then the subgraph of
, then the subgraph of 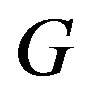 induced by a set of vertices
induced by a set of vertices
 , where
, where  has cohesive order
has cohesive order 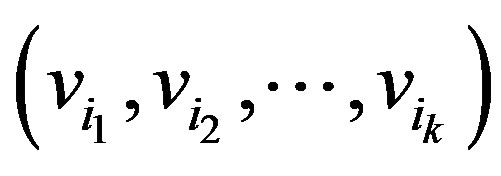 and therefore is a permutation graph. Hence, (a) and (c) are equivalent.
and therefore is a permutation graph. Hence, (a) and (c) are equivalent.
Statement (c) implies statement (d) because a connected component of 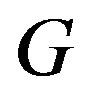 is an induced subgraph of
is an induced subgraph of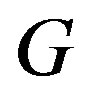 .
.
It remains to show that (d) implies any of (a), (b), (c). Let 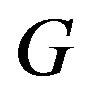 have connected components
have connected components 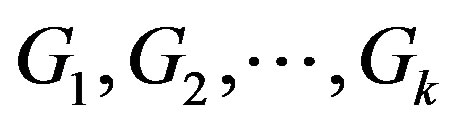 and let
and let  be the order of
be the order of . Let
. Let

be a cohesive order of . Then
. Then
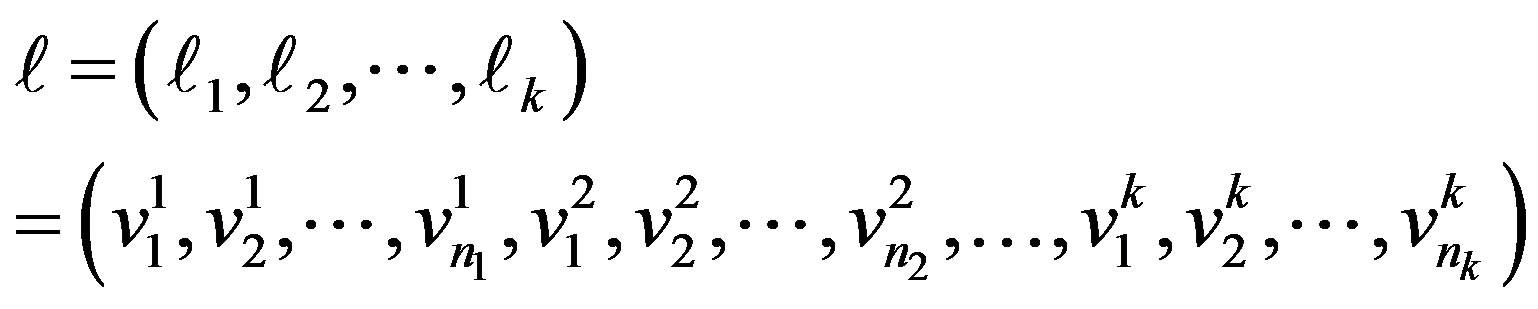
is a cohesive order of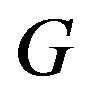 . Therefore
. Therefore  is a permutation graph.
is a permutation graph.
We can now identify permutation graphs through the existence of a cohesive order. Moreover, we can even determine a permutation that generates a permutation graph isomorphic to the graph having a cohesive order.
Paths  and stars
and stars 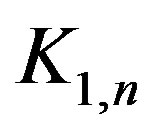 are permutation graphs because they have cohesive orders as illustrated in Figure 4.
are permutation graphs because they have cohesive orders as illustrated in Figure 4.
In the drawing of the path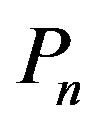 , we have
, we have
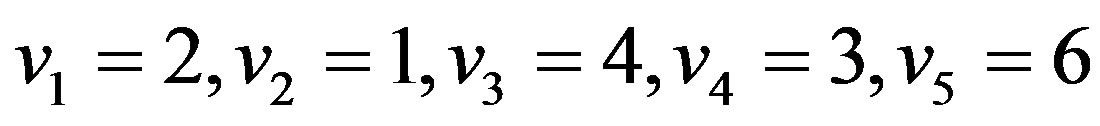 , etc.
, etc.
Condition (a) is vacuously satisfied because there is no pair of arcs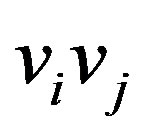 , and
, and  such that
such that . Note for example that
. Note for example that  is an arc and the vertices 1 and 4 are between 2 and 3 in the drawing. We have 1 adjacent to 2 and 4 adjacent to 3. This illustrates condition (b).
is an arc and the vertices 1 and 4 are between 2 and 3 in the drawing. We have 1 adjacent to 2 and 4 adjacent to 3. This illustrates condition (b).
In the drawing of the star 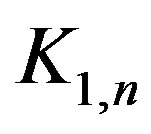 we see that for every arc
we see that for every arc  where
where  all vertices
all vertices 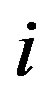 with
with 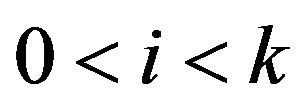 are between
are between 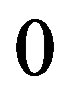 and
and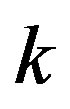 . Moreover, the vertex
. Moreover, the vertex 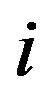 is adjacent to 0. Therefore condition (b) is satisfied. Condition (a) is satisfied vacuously.
is adjacent to 0. Therefore condition (b) is satisfied. Condition (a) is satisfied vacuously.
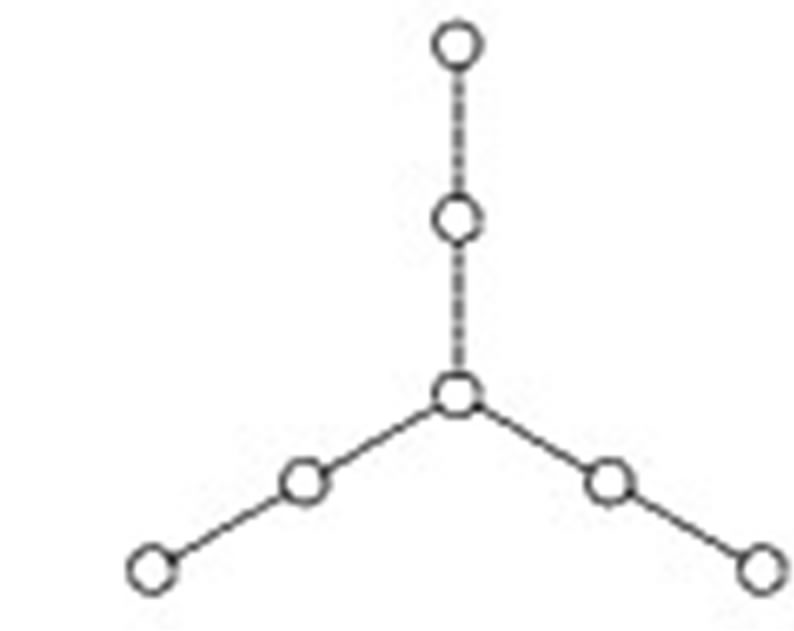
Paths and stars are trees but not all trees are permutation graphs. Consider the tree  formed by subdividing each edge of the star
formed by subdividing each edge of the star 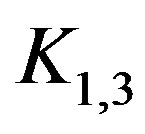 into two edges, as shown in Figure 5.
into two edges, as shown in Figure 5.
It is not difficult to argue indirectly that  has no cohesive order. Therefore this is not a permutation graph. This result is also established by Limouzy [5] where he used the symbol
has no cohesive order. Therefore this is not a permutation graph. This result is also established by Limouzy [5] where he used the symbol 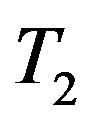 for
for .
.
Harary and Schwenk [9] defined a caterpillar to be a tree with the property that the removal of all pendant vertices results into a path. Figure 6 shows a caterpillar with 25 pendant vertices. The removal of these 25 pendant vertices yields the path .
.
The next lemma is easy and its proof is omitted.
Lemma 3.1 A tree is a caterpillar if and only if it does not contain  as a subgraph.
as a subgraph.
Theorem 3.2 A tree is a permutation graph if and only if it is a caterpillar.
Proof. A tree that contains  is not a permutation
is not a permutation
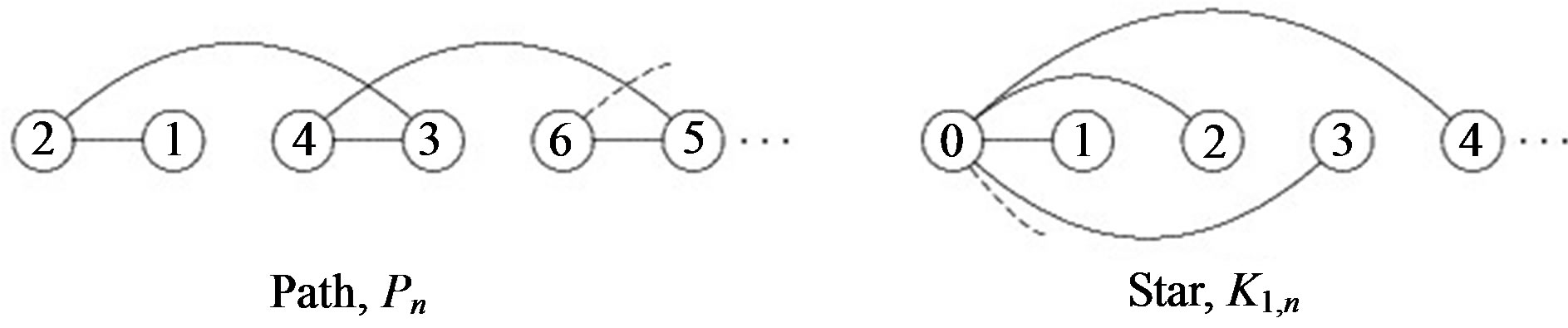
Figure 4. Cohesive order of paths and stars.
Star, K1,3 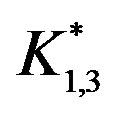
Figure 5. The tree  obtained by subdividing the edges of
obtained by subdividing the edges of .
.

Figure 6. A caterpillar with 25 pendant vertices.
graph because  is not a permutation graph. Therefore, all we need to show is that a caterpillar is a permutation graph. Let
is not a permutation graph. Therefore, all we need to show is that a caterpillar is a permutation graph. Let  be a caterpillar and let
be a caterpillar and let  be the path obtained from
be the path obtained from  by removing the pendant vertices. If
by removing the pendant vertices. If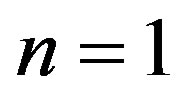 , then
, then  is either the trivial graph or the star
is either the trivial graph or the star  for some
for some . Since the trivial graph and the stars are permutation graphs, we assume that
. Since the trivial graph and the stars are permutation graphs, we assume that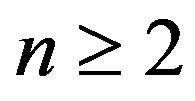 .
.
Let us form the cohesive order of 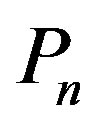 as shown in Figure 4. Let
as shown in Figure 4. Let  be a set of pendant vertices of
be a set of pendant vertices of 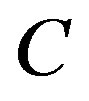 all adjacent to the same vertex
all adjacent to the same vertex 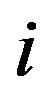 of
of . If
. If 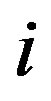 is odd, we insert the vertices in
is odd, we insert the vertices in  immediately to the left of the vertex
immediately to the left of the vertex 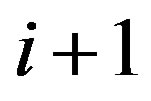 of the path (see Figure 4). If
of the path (see Figure 4). If 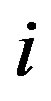 is even we insert the vertices in
is even we insert the vertices in  between
between 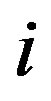 and
and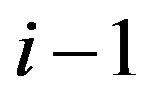 . The result is a cohesive order of
. The result is a cohesive order of . Therefore
. Therefore  is a permutation graph.
is a permutation graph.
Definition 3.1 Let 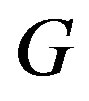 be a graph with vertices
be a graph with vertices  and let
and let  be a collection of arbitrary graphs. The composition by
be a collection of arbitrary graphs. The composition by 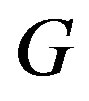 of
of  , denoted by
, denoted by 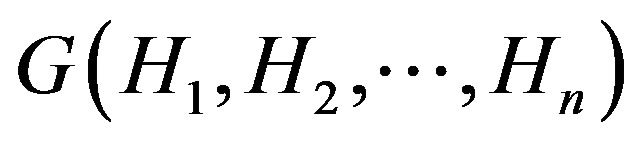 is the graph formed by taking the disjoint union of the graphs
is the graph formed by taking the disjoint union of the graphs  and then adding all edges of the form
and then adding all edges of the form 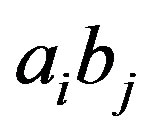 where
where 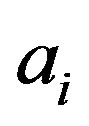 is in
is in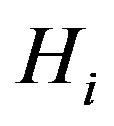 ,
, 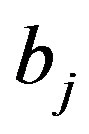 is in
is in  whenever
whenever 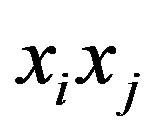 is an edge of
is an edge of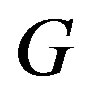 .
.
If each  is equal to a fixed graph
is equal to a fixed graph , we use the symbol
, we use the symbol 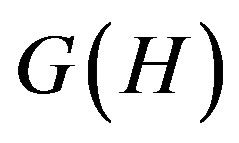 to denote the composition.
to denote the composition.
The sum of two graphs  and
and  , denoted by
, denoted by  is formed by taking the disjoint union of
is formed by taking the disjoint union of 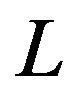 and
and 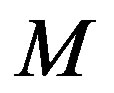 and then adding all edges of the form
and then adding all edges of the form 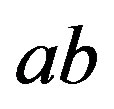 where
where 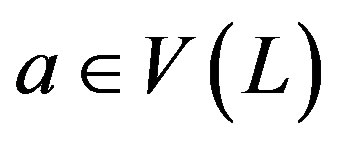 and
and . Thus, the composition
. Thus, the composition 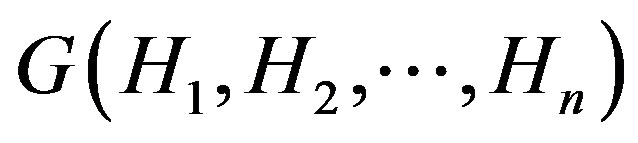 is formed by taking the disjoint union of the graphs
is formed by taking the disjoint union of the graphs 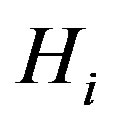 and then forming the sum
and then forming the sum 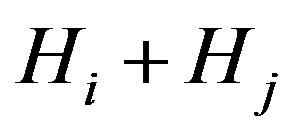 if the associated vertices
if the associated vertices  and
and 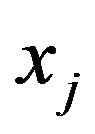 of
of  are adjacent.
are adjacent.
Theorem 3.3 Let 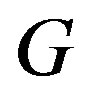 be a graph of order
be a graph of order  and let
and let 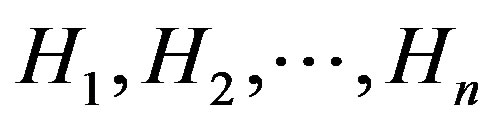 be arbitrary graphs. Then
be arbitrary graphs. Then

is a permutation graph if and only if ,
,  are permutation graphs.
are permutation graphs.
Proof. First, assume that 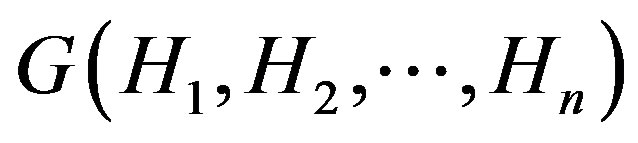 is a permutation graph. Each graph
is a permutation graph. Each graph 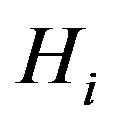 is an induced subgraph of
is an induced subgraph of . Therefore, each
. Therefore, each  is a permutation graph. If we take a vertex
is a permutation graph. If we take a vertex  from each
from each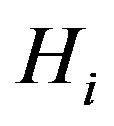 , then the subgraph induced by these vertices is isomorphic to
, then the subgraph induced by these vertices is isomorphic to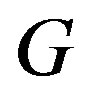 . Therefore
. Therefore 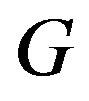 is a permutation graph.
is a permutation graph.
Conversely, assume that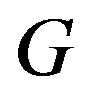 ,
,  are all permutation graphs. Then there is a cohesive order
are all permutation graphs. Then there is a cohesive order  of
of . Let
. Let 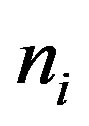 be the order of
be the order of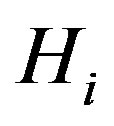 . Then the vertices of
. Then the vertices of  has a cohesive order
has a cohesive order
 .
.
It is easy to check that  is a cohesive order of
is a cohesive order of .
.
Theorem 3.3 actually gives us an easy way of constructing permutation graphs by composition. To illustrate this, let 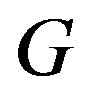 be the star
be the star 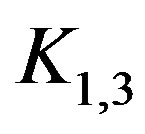 with central vertex
with central vertex 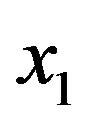 and pendant vertices
and pendant vertices , then
, then
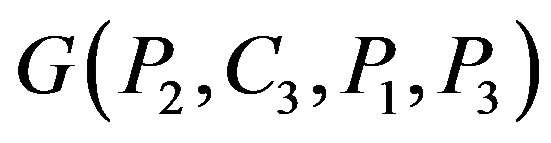
is shown in Figure 7.
All graphs of order at most 4 are permutation graphs [1]. Therefore, 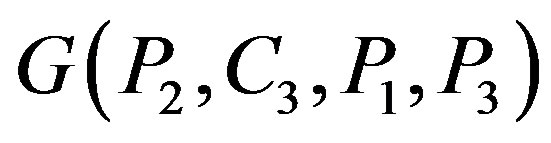 is a permutation graph.
is a permutation graph.
Every graph 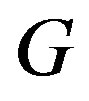 of order
of order  may be written as
may be written as
 and
and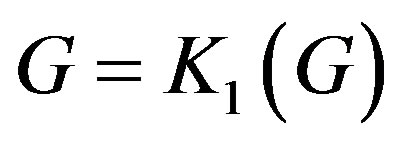 .
.
If these are the only ways 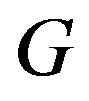 can be written as a composition, then we say that
can be written as a composition, then we say that  is prime.
is prime.
It is easy to see that among the complete graphs, only 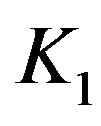 and
and 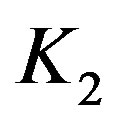 are prime permutation graphs.
are prime permutation graphs.
Among trees with diameter not exceeding 3, it is easy to check that only the paths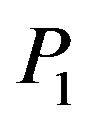 ,
,  , and
, and 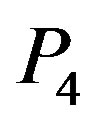 are prime permutation graphs. These are all caterpillars that do not have two pendant vertices adjacent to a common vertex. Note that
are prime permutation graphs. These are all caterpillars that do not have two pendant vertices adjacent to a common vertex. Note that 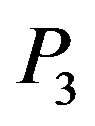 which is excluded from the list is a caterpillar with two pendant vertices having a common neighbor.
which is excluded from the list is a caterpillar with two pendant vertices having a common neighbor.
Theorem 3.4 A tree is a prime permutation graph if and only if it is a caterpillar where no two pendant vertices have a common neighbor.
Proof. In view of our observation about trees with diameter not exceeding 3, we assume throughout that T has diameter at least 4.
Let 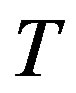 be a tree of order
be a tree of order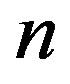 . Assume that
. Assume that  is a prime permutation graph. By Theorem 3.2 T is a caterpillar. Suppose that
is a prime permutation graph. By Theorem 3.2 T is a caterpillar. Suppose that  and
and  are pendant vertices with a common neighbor
are pendant vertices with a common neighbor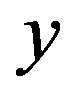 . Let
. Let 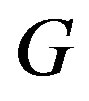 be the tree obtained from
be the tree obtained from 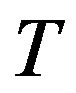 by identifying
by identifying 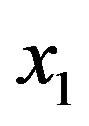 and
and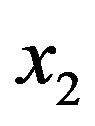 . Let
. Let  be the vertices of
be the vertices of 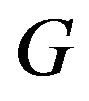 Without loss of generality, assume that
Without loss of generality, assume that 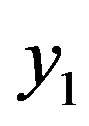 is the vertex resulting from the identification of
is the vertex resulting from the identification of 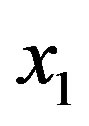 and
and . Let
. Let 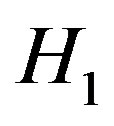 be the graph with two vertices but without an edge, and let
be the graph with two vertices but without an edge, and let  be the trivial graph for
be the trivial graph for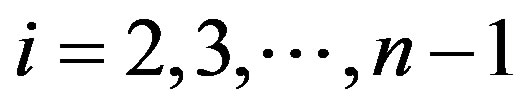 . Then
. Then
 .
.
This contradicts the fact that  is prime.
is prime.

Figure 7. The composition by  of
of .
.
Conversely, assume that  is a caterpillar with no two pendant vertices having a common neighbor. Suppose that
is a caterpillar with no two pendant vertices having a common neighbor. Suppose that 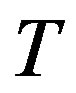 is a not a prime permutation graph. Then for some non-trivial graph
is a not a prime permutation graph. Then for some non-trivial graph 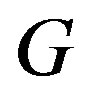 with vertices
with vertices
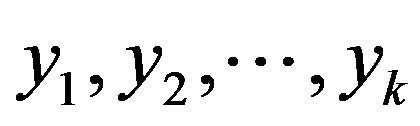 ,
,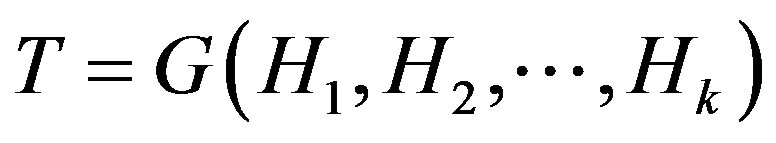 .
.
Without loss of generality, we may assume that 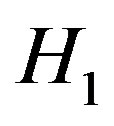 contains at least two vertices. Now,
contains at least two vertices. Now, 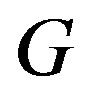 must be connected for otherwise,
must be connected for otherwise, 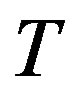 is disconnected. Let
is disconnected. Let  be adjacent to
be adjacent to 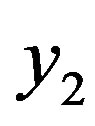 without loss of generality. Then
without loss of generality. Then
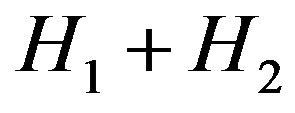
is a subgraph of . If
. If  has at least two vertices, then there will be a cycle in
has at least two vertices, then there will be a cycle in . Therefore,
. Therefore, 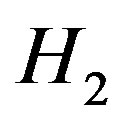 has only one vertex. In
has only one vertex. In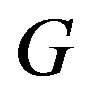 ,
,  cannot be adjacent anymore to any other vertex for otherwise, we would also create a cycle of length 4. Now consider
cannot be adjacent anymore to any other vertex for otherwise, we would also create a cycle of length 4. Now consider . There cannot be adjacent vertices in
. There cannot be adjacent vertices in  for otherwise we will create a cycle of length 3. But then all vertices in
for otherwise we will create a cycle of length 3. But then all vertices in 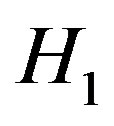 are pendant vertices of
are pendant vertices of 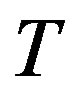 and they have a common neighbor, the vertex in
and they have a common neighbor, the vertex in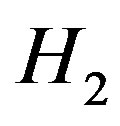 . This is a contradiction.
. This is a contradiction. 
Theorem 3.5 Let  be a decomposable permutation graph. Then there exists a non-trivial prime permutation graph
be a decomposable permutation graph. Then there exists a non-trivial prime permutation graph 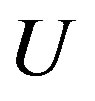 and permutation graphs
and permutation graphs

which are subgraphs of 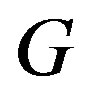 such that
such that
 .
.
Proof. Let
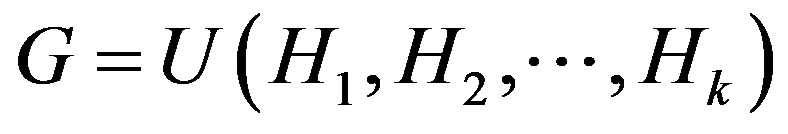
be a decomposition of , where
, where  is non-trivial. If we take one vertex
is non-trivial. If we take one vertex  from each
from each , then the subgraph induced by these vertices is isomorphic to
, then the subgraph induced by these vertices is isomorphic to . Hence,
. Hence,  must be a permutation graph. Each
must be a permutation graph. Each  is an induced subgraph of
is an induced subgraph of . Therefore, each
. Therefore, each  is a permutation graph. Assume that
is a permutation graph. Assume that 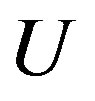 has smallest order among all such decompositions of
has smallest order among all such decompositions of . We claim that
. We claim that 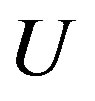 is a prime permutation graph. Suppose that
is a prime permutation graph. Suppose that 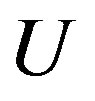 is not prime. Let
is not prime. Let

be a decomposition of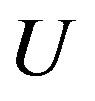 , where
, where 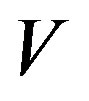 is non-trivial. Since
is non-trivial. Since 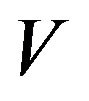 is a decomposition of
is a decomposition of 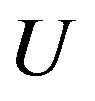 and vertices of
and vertices of 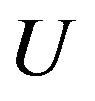 are the induced subgraphs
are the induced subgraphs 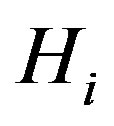 then each
then each 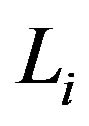 is a associated with subset of
is a associated with subset of . We may assume that
. We may assume that 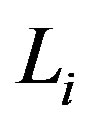 is an induced subgraph of
is an induced subgraph of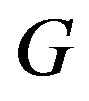 . Hence
. Hence 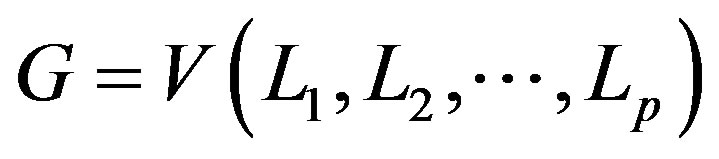 . But this contradicts the choice of
. But this contradicts the choice of . Therefore,
. Therefore, 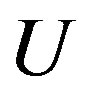 must be a prime permutation graph.
must be a prime permutation graph. 
4. Concluding Remarks
Theorem 3.5 is a fair structural description of a permutation graph. Each 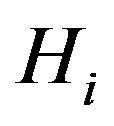 in the decomposition
in the decomposition
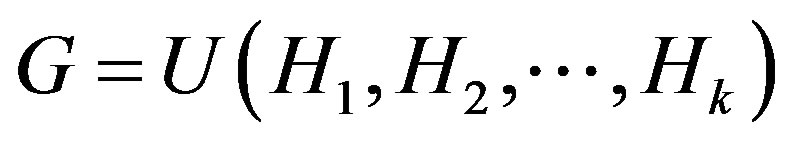
is a permutation graph and so is itself prime permutation graph or a composition of permutation graphs by a prime permutation graph. So we see that a permutation graph is expressible in terms of prime permutation graphs by compositions.
We have determined already the prime permutation trees, given in Theorem 3.4. One interesting problem to consider is the characterization of prime permutation graphs.
REFERENCES
- P. C. F. Ramos, “On Graphs of Inversions of Permutations,” Master’s Thesis, University of the Philippines, Baguio City, 2012.
- S. Skiena, “Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica,” AddisonWesley, Reading, 1990.
- T. Gallai, “Transitiv Orientierbare Graphen,” Acta Mathematica Academiae Scientiarum Hungarica, Vol. 18, No. 1-2, 1967, pp. 25-66. doi:10.1007/BF02020961
- A. Pnueli, A. Lempel and S. Even, “Transitive Orientation of Graphs and Identification of Permutation Graphs,” Canadian Journal of Mathematics, Vol. 23, No. 1, 1971, pp. 160-175. doi:10.4153/CJM-1971-016-5
- V. Limouzy, “Seidel Minor, Permutation Graphs and Combinatorial Properties,” In: Lecture Notes in Computer Science Volume 6506, Springer, Berlin, 2010, pp. 194- 205.
- F. Harary, “Graph Theory,” Addison-Wesley Publishing Company, Boston, 1969.
- J. W. Moon, “Topics on Tournaments,” Holt, Rinehart and Winston, New York, 1968.
- S. V. Gervacio, “Tournament Score Sequences,” Annals of the New York Academy of Sciences, Vol. 576, Graph Theory and Its Applications, East and West: Proceedings of 1st China-USA International Graph Theory Conference, Jinan, China, June 1986, pp. 200-202.
- F. Harary and A. J. Schwenk, “The Number of Caterpillars,” Discrete Mathematics, Vol. 6, No. 4, 1973, pp. 359- 365. doi:10.1016/0012-365X(73)90067-8

