ABSTRACT

The edge-domsaturation number ds'(G) of a graph G = (V, E) is the least positive integer k such that every edge of G lies in an edge dominating set of cardinality k. In this paper, we characterize unicyclic graphs G with ds'(G) = q – Δ'(G) + 1 and investigate well-edge dominated graphs. We further define γ'^–-critical, γ'⁺-critical, ds'^–-critical, ds'⁺-critical edges and study some of their properties.

1. Introduction

Throughout this paper, G denotes a graph with order p and size q. By a graph we mean a finite undirected graph without loops or multiple edges. For graph theoretic terms we refer Harary [1] and in particular, for terminology related to domination theory we refer Haynes et al. [2].

1.1. Definition

Let G = (V, E) be a graph. A subset D of E is said to be an edge dominating set if every edge in E-D is adjacent to at least one edge in D. An edge dominating set D is said to be a minimal edge dominating set if no proper subset of D is an edge dominating set of G. The edge domination number γ'(G) of a graph G equals the minimum cardinality of an edge dominating set of G. An edge dominating set of G with cardinality γ'(G) is called a γ'(G)-set or γ'-set.

Acharya [3] introduced the concept of domsaturation number ds(G) of a graph. For any graph G of order p, and for any integer r such that γ(G) ≤ r ≤ p, we call the set 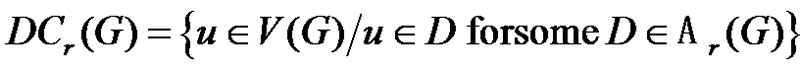the r-level domination core of G. We say that G is r-level domination-saturated (or in short, “r-domsaturated”) if DC_r(G) – V(G). The domsaturation number ds(G) is then defined by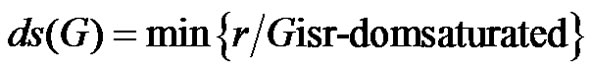. Arumugam and Kala [4] observed that for any graph G, 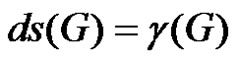or 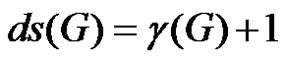and obtained several results on ds(G). We now extend the concept of domsaturation number of a graph to edges.

1.2. Definition

The least positive integer k such that every edge of G lies in an edge dominating set of cardinality k is called the edge-domsaturation number of G and is denoted by ds'(G).

If G is a graph with edge set E and D is a γ'-set of G, then for any edge e Î E-D, is also an edge dominating set and hence 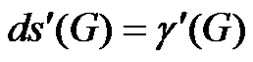or.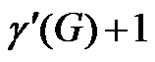

Thus we have the following definition.

1.3. Definition

A graph G is said to be of class 1 or class 2 according as 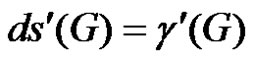or.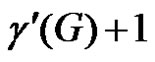

1.4. Definition

An edge e of G is

1) γ'-critical if;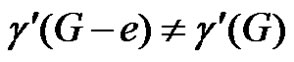

2) γ'⁺-critical if;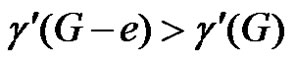

3) γ'^–-critical if;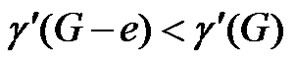

4) γ'-fixed if every γ'-set contains e;

5) γ'-free if there exists γ'-sets containing e and also γ'-sets not containing e;

6) γ'-totally free if there is no γ'-set containing e.

We use the following theorem.

1.5. Theorem [5]

For any connected unicyclic graph 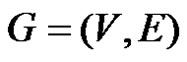with cycle C, 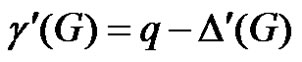if and only if one of the following holds.

1);

2), 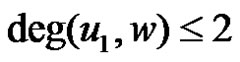for all vertices w not on C and 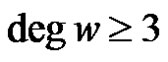for at most one vertex w not on C;

3)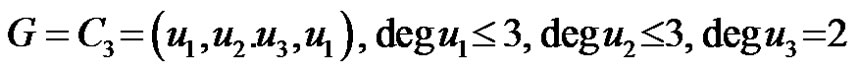 all the vertices not on C adjacent to u₁ have degree at most 2 and all vertices whose distance from u₁ is 2 are pendent vertices;

4) 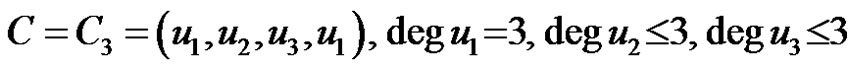and all vertices not on C are pendent vertices;

5);

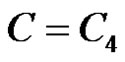6)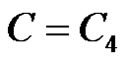, either exactly one vertex of C has degree at least 3 and all vertices not on C are pendent vertices.

2. Main Results

2.1. Lemma

An edge e of G is γ'^–-critical if and only if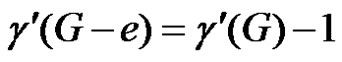

Proof

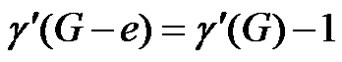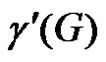For any edge e, we observe that or or. Now, suppose e is γ'^–-critical. Then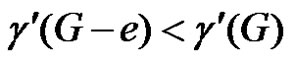. Hence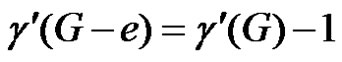. The converse is obvious.

2.2. Theorem

An edge e is γ'^–-critical if and only if

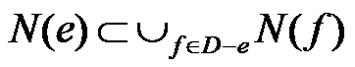(1)

for some γ'-set D containing e.

Proof

If e is γ'^–-critical, 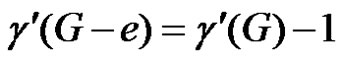by lemma 2.1. Let S be a γ'-set of G – e. If S contains an edge of N(e), then S will be an edge dominating set of G and hence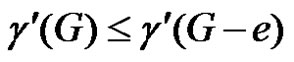, a contradiction. Thus S does not contain any edge of N(e). Since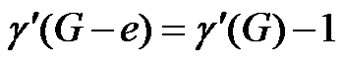, 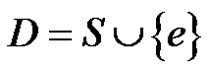is a γ'-set of G and so Equation (1) holds. Conversely, suppose e is an edge such that (1) is true. Then G – e is an edge dominating set of G – e and hence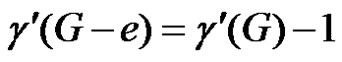. Thus e is γ'^–-critical.

2.3. Theorem

Let G be a graph without isolated edges. An edge e in G is γ'^–-critical if and only if 1) e is γ'-free, and 2) no γ'-set of G – e contains any edge of N(e).

Proof

If e is γ'^–-critical, then 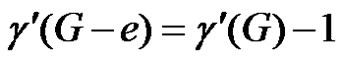by Lemma 2.1. As in theorem 2.2, if S is any γ'-set of G – e, then S will not contain any edge of N(e) and 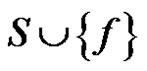is a γ'- set of G for every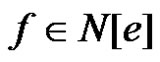. This implies that e is γ'-free. Conversely, suppose (1) and (2) are true. Let S be a γ'- set of G – e. By (2) S does not contain any edge of N[e]. Hence S cannot be an edge dominating set of G. But, for any edge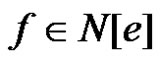, 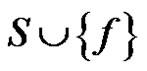is an edge dominating set of G. Since S is a minimum edge dominating set for G – e, 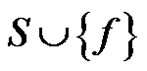is also a minimum edge dominating set for G and hence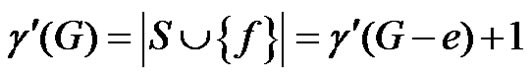. Thus e is γ'^–-critical.

2.4. Theorem

Let G be a graph and. Then

1) e is γ'-fixed if and only if there exists no edge dominating set of G – e with γ'(G) edges which is also an edge dominating set of G.

2) e is γ'-totally free if and only if every γ'-set of G is a γ'-set of G – e.

Proof

1) Assume that e is γ'-fixed. Suppose there exists an edge dominating set S of G – e with 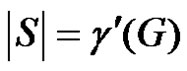which is also an edge dominating set of G. Then S is a γ'-set not containing e which is impossible as e is γ'-fixed. The converse is obvious.

2) Let e be γ'-totally free. Then e does not belong to any γ'-set of G and so every γ'-set D of G is an edge dominating set of G – e. Thus. If, then by theorem 2.3, e is γ'-free and so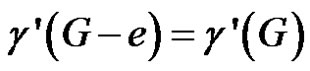, D is a γ'-set of G – e. The converse is obvious.

2.5. Theorem

Let G be a connected graph. If a cut edge e of G is γ'- fixed, then e is γ'⁺-critical

Proof

Let S be a γ'-set of G. Let e be a cut edge that is γ'- fixed. Then e belongs to every γ'-set. Since e is a cut edge, G – e is a disconnected graph with at least two components G' and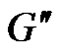. Let e' and e" be the neighbors of e in G' and G" respectively. Therefore 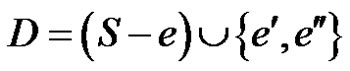is a minimum edge dominating set of G – e so that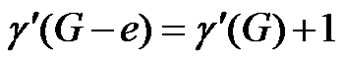. Hence e is γ'⁺-critical.

2.6. Theorem

An edge e in a graph G is γ'⁺-critical if and only if 1) e is not isolated edge 2) e is γ'-fixed and 3) There is no edge dominating set for 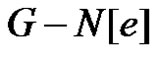having γ'(G) edges which also dominates N[e].

Proof

If e is γ'⁺-critical, then, by lemma 2.1. Clearly e is not an isolated edge. If S is a γ'-set of having γ'(G) edges which also dominates N(e) then, a contradiction. Thus no edge dominating set of 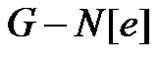having γ'(G) edges can dominate N(e). By Theorem 2.4, e is γ'-fixed. The converse is obvious.

We now investigate relationships between, γ'-free edges, γ'-totally free edges and graphs which are class 1 and class 2.

2.7. Theorem

If G is a graph without isolated edges, then G is of class 2 if and only if G has γ'-totally free edges.

Proof

Suppose G has a γ'-totally free edge e. By Theorem 2.4 (2), G is of class 2. Conversely, suppose G is of class 2. Then there exists an edge e which is not in any γ'-set. Hence every γ'-set of G is also a γ'-set of G – e so that e is γ'-totally free.

2.8. Theorem

Proof

Let G be a connected graph. If G has a γ'-fixed edge, then it has a γ'-totally free edge.

Suppose G has a γ'-fixed edge e. Then e belongs to every γ'-set.

Claim: No neighbor of e belongs to any γ'-set of G. Suppose at least one of its neighbor say e' belongs to a γ'- set D. Let 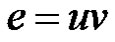and e' be incident with u. Then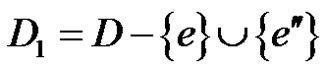, where e" is any edge incident with v is an edge dominating set of G – e with γ'-edges which is also an edge dominating set of G. But by Theorem 2.6, this is a contradiction, since e is a γ'-fixed edge. Therefore no neighbor of e belongs to any γ'-set of G. Thus neighbors of e are all γ'-totally free in G.

We now investigate the class of graphs which are ds'⁺, ds'^–-critical.

2.9. Lemma

Let e Î E(G). If e is γ'-totally free and G – e is of class 1, then.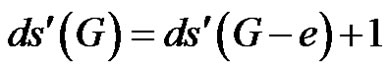

Proof

Since e is γ'-totally free, by Theorem 2.4,

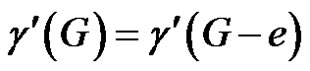(1)

Since e is γ'-totally free, by Theorem 2.3, G is of class 2 and so

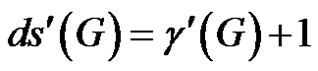(2)

Since G – e is of class 1, we have

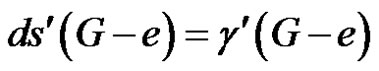(3)

From Equations (1), (2) and (3), we have

.

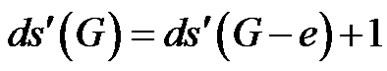2.10. Lemma

Let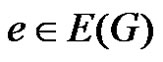. If e is γ'-totally free and G – e is of class 2, then.

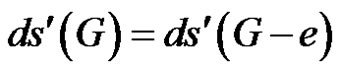Proof

If e is γ'-totally free, then by Theorem 2.4,

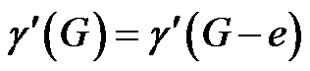(1)

Since G and G – e are of class 2, we have

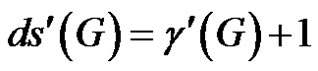(2)

and

(3)

From equations (1), (2) and (3), we have

.

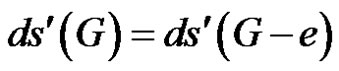2.11. Lemma

Let e be an edge of G. If e is γ'-free and G – e is of class 1, then 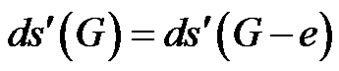or.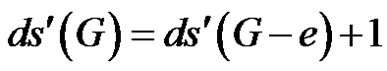

Proof

Suppose e is a γ'-free edge. In any case G is either of class 1 or class 2.

Case (1). G is of class 1.

Let S be a γ'-set of G – e. If S does not contain any neighbor of e, then every neighbor of e is γ'-totally free in G – e. This implies that G – e is of class 2. But this is a contradiction and so S must contain a neighbor of e. Then by theorem 2.4,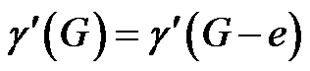. Since G and G – e are of class 1, we have

.

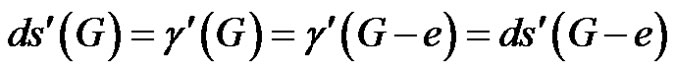Case (2). G is of class 2.

Since G – e is of class 1, then by a similar argument, S must contain a neighbor of e. Since G is of class 2, we have.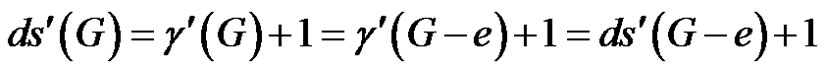

2.12. Lemma

Let e be an edge of G. If e is γ'-free and G – e is of class 2, then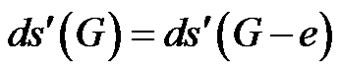, 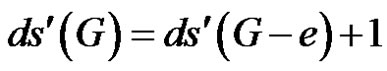or.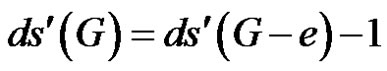

Proof

Case (1). G is of class 1.

Let S be a γ'-set of G – e. We have the following cases:

Subcase (1). S contains a neighbor of e.

Now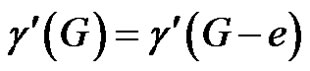. Since G is of class 1 and G – e is of class 2, we have.

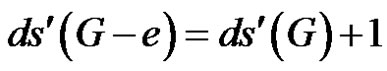Subcase (2). S does not contain a neighbor of e.

Now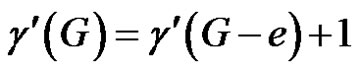. Since G – e is of class 2 and G is of class 1, we have.

Case (2). G is of class 2.

By an argument similar to that in case (1), we have 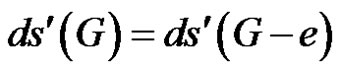or.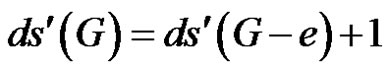

2.13. Lemma

Let e be an edge of G. If e is γ'-fixed and G – e is of class 1, then.

Proof

If e is γ'-fixed, then by Theorem 2.8, all of its neighbors are γ'-totally free. Then by Theorem 2.7, G is of class 2 and hence

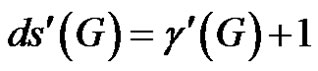(1)

As e is γ'-fixed, by Theorem 2.4,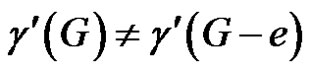. If, then e is γ'-critical. Then by Lemma 2.11, e is γ'-free and this is a contradiction. Therefore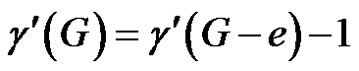. Since G is of class 2 and G – e is of class 1, we have.

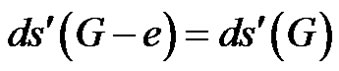2.14. Lemma

Let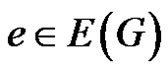. If e is γ'-fixed and G – e is of class 2, then.

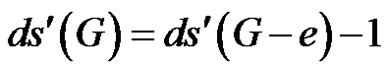Proof

By an argument analogous to that in Lemma 2.13, since G – e is of class 2, we have.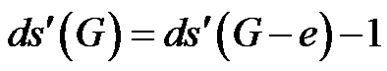

2.15. Theorem

Let G be a graph without isolated edges. An edge e in G is ds'^–-critical if and only if one of the following holds.

1) e is γ'-totally free and G – e is of class 1.

2) e is γ'-free, G is of class 2 and G – e is of class 1.

3) e is γ'-free and both G and G – e are of class 2.

Proof

Suppose e is ds'^–-critical. Then

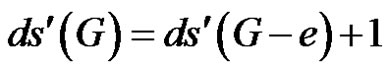(1)

Let S be a γ'-set of G. Then we have the following cases:

Case (1). G and G – e are of class 1.

By (1),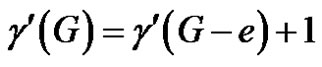. By theorem 2.3, e is γ'- free and no γ'-set of G-e contains any edge of N(e). Now every neighbor of e is γ'-totally free in G – e. Therefore G – e is of class 2, which is a contradiction.

Case (2). G is of class 1 and G – e is of class 2.

Then Equation (1) becomes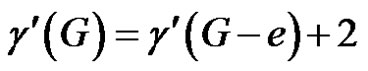. But this is not possible.

Case (3). G is of class 2 and G – e is of class 1.

Then Equation (1) becomes. Then either e is γ'-free or γ'-totally free.

Case (4). G and G – e are of class 2.

In this case, Equation (1) becomes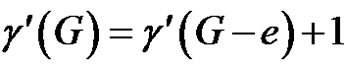. Then by theorem 2.3, e is γ'-free.

From Lemmas 2.9, 2.11 and 2.12, the converse is true.

2.16. Theorem

Let G be a graph without isolated edges. An edge e in G is ds'⁺-critical if and only if one of the following holds.

1) e is γ'-free, G is of class 1 and G – e is of class 2.

2) e is γ'-fixed and G – e is of class 2.

Proof

Suppose e in G is ds'⁺-critical. Hence

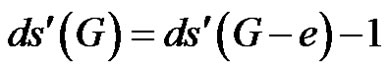(1)

Let S be a γ'-set of G. Then we have the following cases:

Case (1). G and G-e are of class 1.

From equation (1) 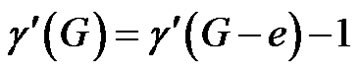and so G is γ'⁺-critical. Hence by Theorem 2.6, e is γ'-fixed, which is a contradiction.

Case (2). G is of class 1 and G – e is of class 2.

Now equation (1) becomes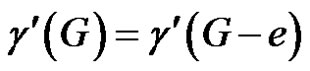. Then S must contain a neighbor of e. Since G is of class 1, e is γ'-free.

Case (3). G is of class 2 and G – e is of class 1.

Then Equation (1) becomes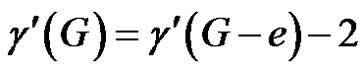, which is not possible.

Case (4). G is of class 2 and G – e is of class 2.

In this case, Equation (1) becomes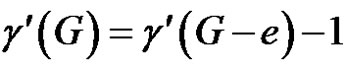. Then by Theorem 2.4, e is γ'-fixed.

Conversely, suppose if (1) or (2) is true. Then by case (1) of Lemma 2.12 and Lemma 2.14, the result follows.

3. Edge-Domsaturation Number of a Graph

Theorem

For any connected unicyclic graph 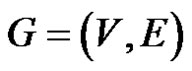with cycle C, 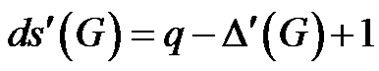if and only if one of the following holds.

1)

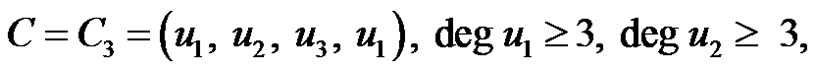
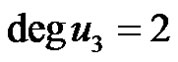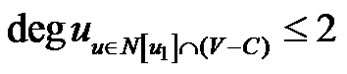, and there exists

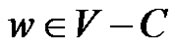such that, i = 1, 2.

2) 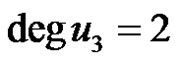, exactly one vertex w not on C has 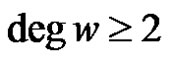and remaining vertices are pendent vertices.

Proof

Suppose.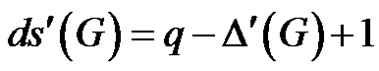

Let be the unique cycle in G.

If, then 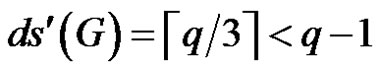for all n ≥ 3 and so.

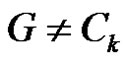Let S denote the set of all pendent edges of G and let.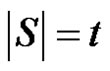

Claim 1: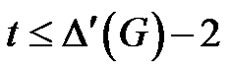. Since 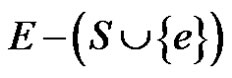is an edge dominating set for any edge e of C,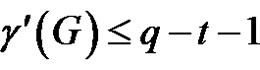. For any pendent edge f, 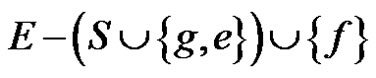is an edge dominating set of G containing f. Here g is an edge adjacent to f and e is any edge of the cycle. Hence, so that.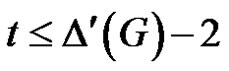

Claim 2: e = uv is an edge with degree ∆'. Then either u or v lies on C_k.

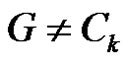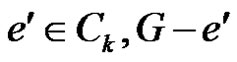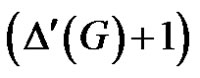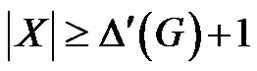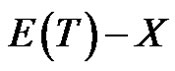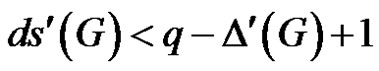Now let and be an edge of maximum degree ∆'. If e Î C_k, then for some edge  is a tree T of G with at least pendent edges. If X is the set of all pendent edges of G – e, then . Then is an edge dominating set of cardinality at most. Therefore , which is a contradiction.

Case (1). u or v lies on C.

Claim 3: 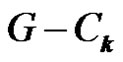is the union of P₁ and P₂. Suppose not. Then, 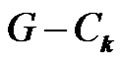contains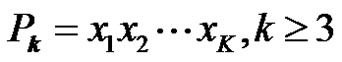. Suppose 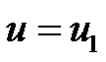lies on C_K. Let 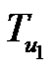be the maximal tree rooted at u₁ not containing any edge of C_k. Clearly 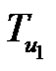has at least ∆'(G) – 2 pendent edges, say S. Then

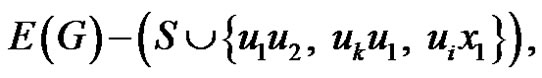is an edge dominating set of cardinality less than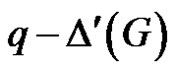. Therefore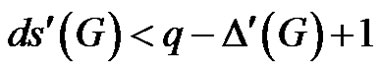, which is a contradiction.

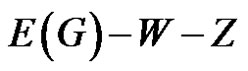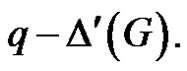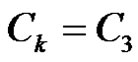In this case, G has at least ∆' – 2 pendent edges. Let W be the set of these pendent edges. Further  and let Y denote a γ'-set of C_k. Let. If k > 4, then is an edge dominating set of cardinality less than Hence or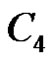. Since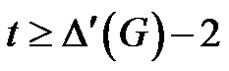. By claim 1,.

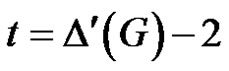Subcase (1).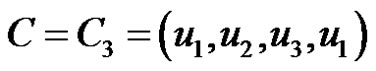

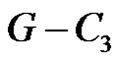is the union of P₁ and P₂. Also u or v lies on C. Let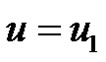. Therefore 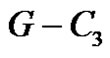contains at least one P₂. Since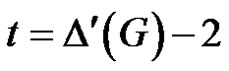, no other vertex other than u and v has degree > 3.

If G – C₃ is the union of 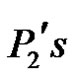alone, then 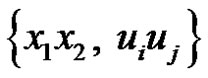or 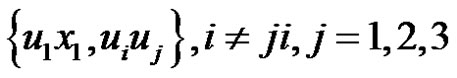is an edge dominating set and every edge lies in a γ'-set. Therefore.

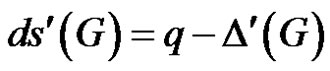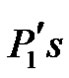If is the union of and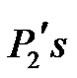, then from Theorem 1.5,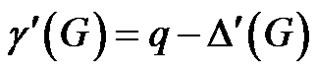. But pendent edges adjacent to u₁ does not lie in any γ'-set. Therefore.

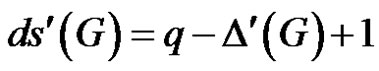Subcase (2).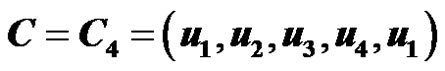

As in subcase (1), G – C₄ also contains P₂. Then is an edge dominating set of cardinality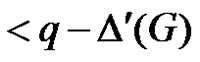. Therefore.

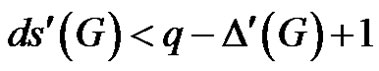Case (2). u and v lies on C.

Claim 4: G – C_k is the union of P₁ and P₂.

Suppose not. Then, G – C_k contains 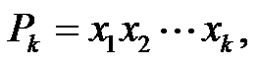. Suppose 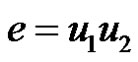lies on C_k. Let .

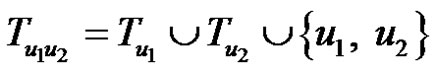Clearly 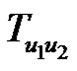has at least 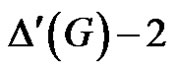pendent edges, say P.

Then 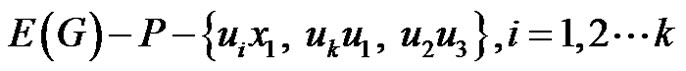is an edge dominating set of cardinality less than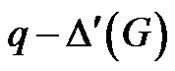. Therefore, which is a contradiction.

As in case (1),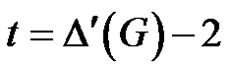. Let 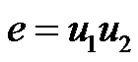be an edge of maximum degree.

Subcase (1).

In this case, from Theorem 1.5, (3), u₃u₁ does not belong to any γ'-set. Therefore.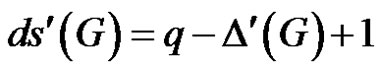

Subcase (2).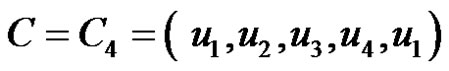

From Theorem 1.5, there does not exist an edge dominating set of cardinality.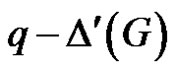

The converse is obvious.

4. Well-Edge Dominated Graph

A graph G is called well dominated if all minimal dominating sets have the same cardinality. This concept was introduced by Finbow, Hartnell and Nowakowski [6].

4.1. Definition

A graph G is well-edge dominated if every minimal edge dominating set of G has the same cardinality.

4.2. Lemma

If G is a well-edge dominated graph and e is an edge of G, then there exists a minimum edge dominating set containing e and a minimum edge dominating set not containing e.

Proof

To obtain an edge dominating set containing e, place e in the set D, delete 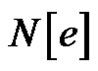from G and continue in this greedy fashion until there are no edges left. Then D is minimal and since G is well-edge dominated, it is minimum.

To obtain a minimum edge dominating set not containing e, we use the same greedy method except that we use a neighbor of e as our initial edge in D.

4.3. Theorem

If G is well-edge dominated, then G is of class 1.

Proof

From the above lemma, it is clear that every edge belongs to any one of the γ'-set. Therefore G is of class 1.

REFERENCES