Open Journal of Discrete Mathematics
Vol.2 No.2(2012), Article ID:18873,4 pages DOI:10.4236/ojdm.2012.22014
Global Behavior of a Nonlinear Difference Equation with Applications
Institute of Systems Science and Mathematics, Naval Aeronautical and Astronautical University, Yantai, China
Email: dczhang1967@tom.com, ytliyingwang@163.com
Received January 25, 2012; revised February 27, 2012; accepted March 15, 2012
Keywords: Difference Equation; Recursive Sequence; Period-3 Solution
ABSTRACT
In this paper, solutions of difference equation 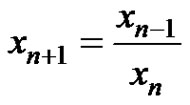 for
for 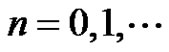 are investigated, where
are investigated, where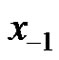 ,
, 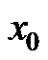 are both arbitrary nonzero real numbers. The results are applied to the following difference equation
are both arbitrary nonzero real numbers. The results are applied to the following difference equation 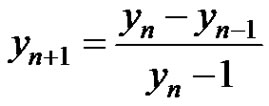 for
for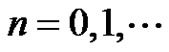 .
.
1. Introduction
Amleh, Grove and Ladas [1] studied the global stability boundedness character and periodic nature of positive solutions of difference equation
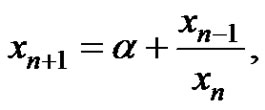 (1)
(1)
where 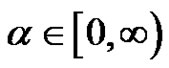 and initial conditions
and initial conditions 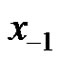 and
and  are both arbitrary positive real numbers.
are both arbitrary positive real numbers.
Amleh, Grove and Ladas [1] obtain the following theorem.
Theorem A (Amleh, Grove and Ladas [1]) Let
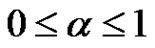 and
and 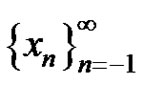 be a solution of equation (1)
be a solution of equation (1)
with initial conditions 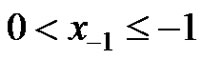 and
and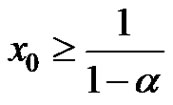 .
.
Then the following statements are true.
1) 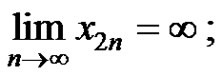
2)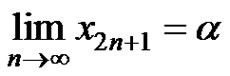 .
.
Now, we can see that if  and
and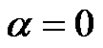 , then
, then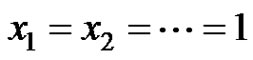 . So, the theorem A does not hold for
. So, the theorem A does not hold for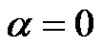 .
.
Kulenovic and Glass in their monograph [2] give an open problem as follows.
Open Problem 6.10.7. For the following difference equation determine the “good” set 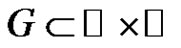 of the initial conditions
of the initial conditions 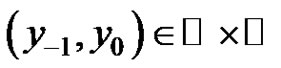 throng with the equation is well defined for all
throng with the equation is well defined for all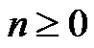 . Then for every
. Then for every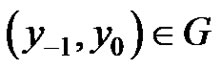 , investigate the long-term behavior of the solution
, investigate the long-term behavior of the solution  of
of
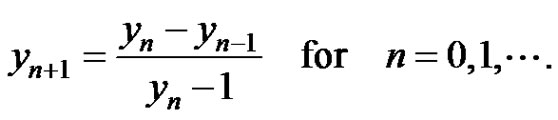 (2)
(2)
Let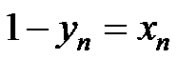 . Then equation (2) can be rewritten as follows
. Then equation (2) can be rewritten as follows
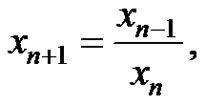 (3)
(3)
where 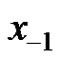 and
and 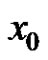 are arbitrary nonzero real numbers. To this end, we study equation (3) and use the results of equation (3) to equation (2).
are arbitrary nonzero real numbers. To this end, we study equation (3) and use the results of equation (3) to equation (2).
2. Some Lemmas
It is easy for one to see that if
then we have
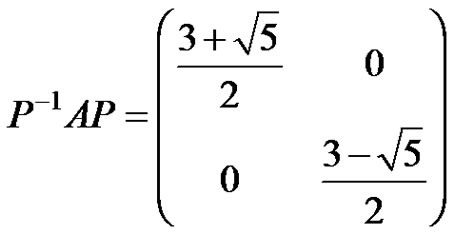 (4)
(4)
and

Lemma 2.1 (Kocic and Ladas [3]) Consider the difference equation
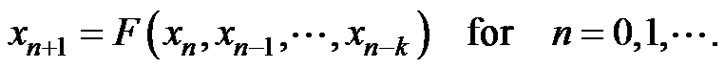 (5)
(5)
Assume that  is a
is a  function and
function and  is an equilibrium of equation (5).
is an equilibrium of equation (5).
Then the linearized equation associated with equation (5) about the equilibrium 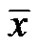 is
is

and the following statements are true.
a) If all roots of the polynomial equation
 (6)
(6)
lie in the open unit disk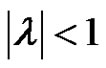 , then the equilibrium
, then the equilibrium 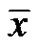 of equation (5) is asymptotically stable;
of equation (5) is asymptotically stable;
b) If at least one root of equation (6) has absolute value greater than one, then equilibrium 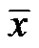 of equation (5) is unstable.
of equation (5) is unstable.
One can refer to Kocic and Ladas [3, Corallary 1.3.2, p14 ].
Lemma 2.2 Equation (3) has two equilibriums  and
and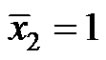 .
.
It is easy to see that  has two roots and the proof is complete.
has two roots and the proof is complete.
3. Main Results
Theorem 3.1 Let 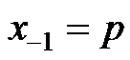 and
and . Then the following statements are true.
. Then the following statements are true.
a) , where
, where
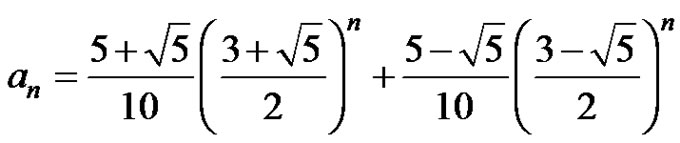
and
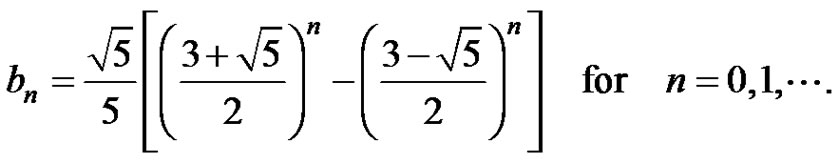
b)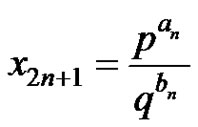 , where
, where

and
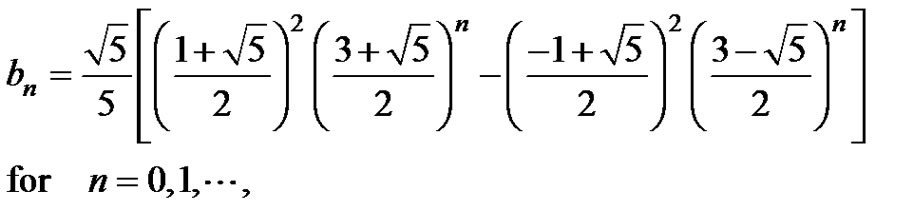
where  is the solution of equation (3) with the initial
is the solution of equation (3) with the initial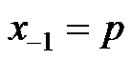 ,
,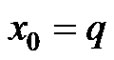 .
.
Proof: Part a).
Let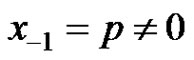 ,
,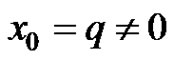 . Then by equation (3) we have
. Then by equation (3) we have
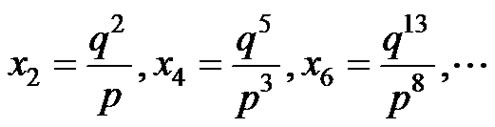
we assume that
 (7)
(7)
Then by induction, we have
 (8)
(8)
where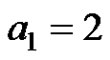 ,
, 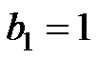 and
and 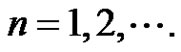
Change equation (8) into
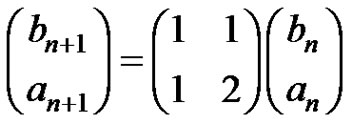 (9)
(9)
or
 (10)
(10)
where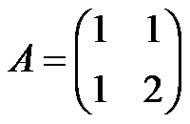 .
.
From equation (4), we get
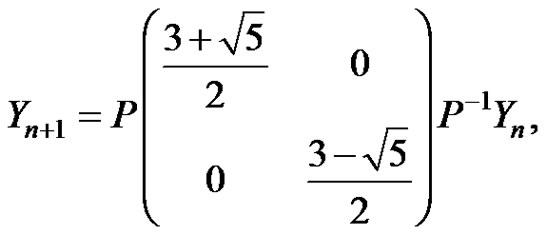 (11)
(11)
where
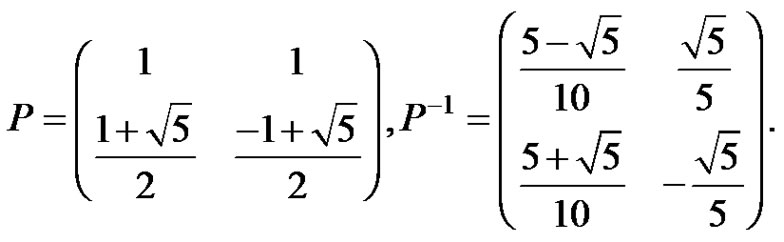
Equation (11) can be changed into

Let 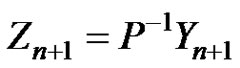 and
and . Then we obtain that
. Then we obtain that
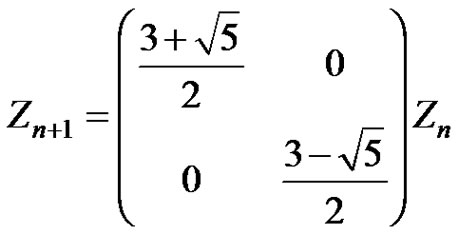 (12)
(12)
and 
By induction, we have
 (13)
(13)
Therefore,

Hence, the proof of part (a) is complete.
The proof of part (b) can be similarly given, so we omit it. This can complete the proof of theorem 3.1.
By theorem 3.1, we get the following corollary.
Corollary 3.1 Assume that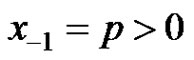 ,
,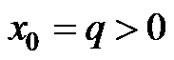 . Then the following statements are true.
. Then the following statements are true.
a) If , then the positive solution
, then the positive solution 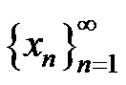 of equation (3) converges to 1, i.e,
of equation (3) converges to 1, i.e,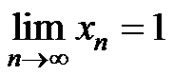 .
.
b) If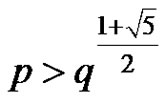 , then the positive solution
, then the positive solution 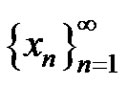 of equation (3) has the properties
of equation (3) has the properties

c) If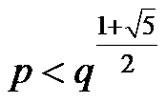 , then the positive solution
, then the positive solution 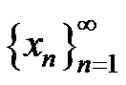 of equation (3) has the properties
of equation (3) has the properties

Theorem 3.2 Assume that ,
,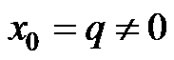 . Then the following statements are true.
. Then the following statements are true.
a) If  and
and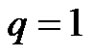 , then the solution
, then the solution 
of equation (3) is periodic with period-3 as follows
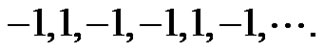 (14)
(14)
b) If 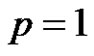 and
and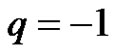 , then the solution
, then the solution 
of equation (3) is periodic with period-3 as follows
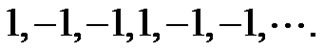 (15)
(15)
c) If 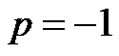 and
and , then the solution
, then the solution  of equation (3) is periodic with period-3 as follows
of equation (3) is periodic with period-3 as follows
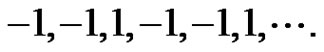 (16)
(16)
The proof of theorem 3.2 is very easy, so we will omit it.
By theorems 3.1 and 3.2, we can obtain the following corollary.
Corollary 3.2 Assume that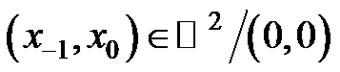 . Then the following statements are true.
. Then the following statements are true.
a) If 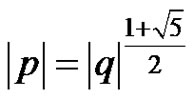 and at least one of p and q is less than 0, then
and at least one of p and q is less than 0, then  of equation (3) converges to a period-3 solution of equation (3) as one of (10)-(12).
of equation (3) converges to a period-3 solution of equation (3) as one of (10)-(12).
b) If 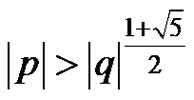 and at least one of p and q is less than 0, then
and at least one of p and q is less than 0, then 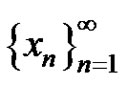 of equation (3) has the following properties
of equation (3) has the following properties

c) If  and at least one of p and q is less than 0, then
and at least one of p and q is less than 0, then 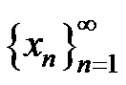 of equation (3) has the following properties
of equation (3) has the following properties
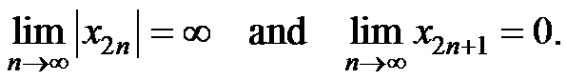
d) If at least one of p and q is less than 0, then every solution of equation (3) strictly oscillates about the equilibrium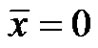 .
.
e) If 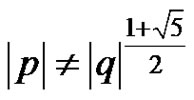 and at least one of p and q is less than 0, then every solution of equation (3) strictly oscillates about the equilibrium
and at least one of p and q is less than 0, then every solution of equation (3) strictly oscillates about the equilibrium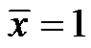 .
.
Theorem 3.3 The equilibrium 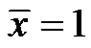 of equation (3) is unstable.
of equation (3) is unstable.
Proof: The linearize equation associated with equation (3) about the equilibrium  is
is
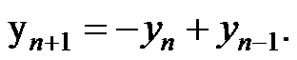 (17)
(17)
The characteristic equation of (17) is
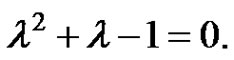
Thus, we obtain two roots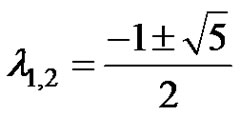 . Noting that
. Noting that . Therefore, by lemma 3.1, we know that the equilibrium
. Therefore, by lemma 3.1, we know that the equilibrium  of equation (3) is unstable. The proof of theorem 3.3 is complete.
of equation (3) is unstable. The proof of theorem 3.3 is complete.
4. Application
By theorem 3.1, we have the following theorem.
Theorem 4.1 Assume that 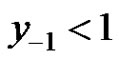 and
and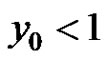 . Then the following statements are true.
. Then the following statements are true.
a) Every solution 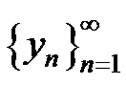 of equation (2) satisfies
of equation (2) satisfies 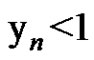 for
for 
b) If , then the solution
, then the solution 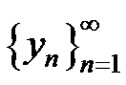
of equation (2) converges to 0.
c) If , then the solution
, then the solution 
of equation (2) has the following properties
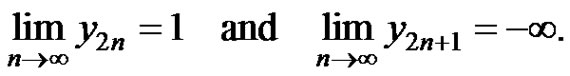
d) If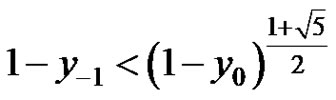 , then the solution
, then the solution 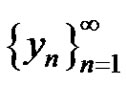
of equation (2) has the following properties
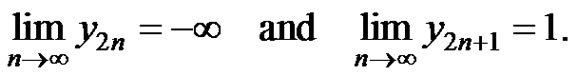
By corollary 3.2, we get the following theorem.
Theorem 4.2 Assume that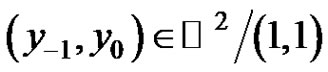 . Then the following statements are true.
. Then the following statements are true.
a) If 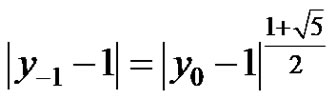 and at least one of
and at least one of 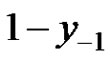
and  is less than 0, then
is less than 0, then 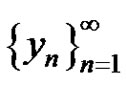 of equation (2) converges to a period-3 solution of equation (2) as one of the following:
of equation (2) converges to a period-3 solution of equation (2) as one of the following:
i) 
ii) 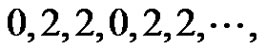
iii) 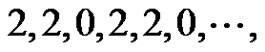
b) If  and at least one of
and at least one of 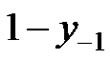
and 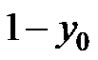 is less than 0, then every solution
is less than 0, then every solution  of equation (2) has the following properties:
of equation (2) has the following properties:
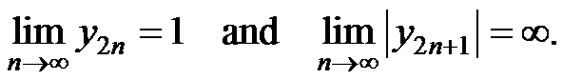
c) If 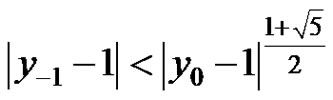 and at least one of
and at least one of 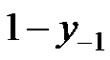
and 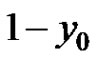 is less than 0, then every solution
is less than 0, then every solution  of equation (2) has the following properties:
of equation (2) has the following properties:
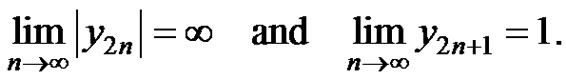
d) If 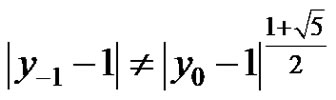 and at least one of
and at least one of 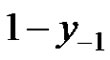
and 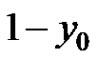 is less than 0, then every solution
is less than 0, then every solution  of equation (2) strictly oscillates about the equilibrium
of equation (2) strictly oscillates about the equilibrium 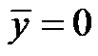 of equation (2).
of equation (2).
5. Acknowledgements
Research supported by Distinguished Expert Foundation and Youth Science Foundation of Naval Aeronautical and Astronautical University.
REFERENCES
- A. M. Amleh, E. A. Grove and G. Ladas, “On the Recursive Sequence
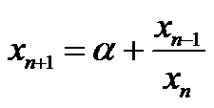 ,” Journal of Mathematical Analysis and Applications, Vol. 233, No. 2, 1999, pp. 790-798. doi:10.1006/jmaa.1999.6346
,” Journal of Mathematical Analysis and Applications, Vol. 233, No. 2, 1999, pp. 790-798. doi:10.1006/jmaa.1999.6346 - M. R. S Kulenovic and L. Glass, “Dynamics of Second Order Rational Difference Equations,” Chapman Hall/ CRC, USA, 2002.
- V. L. Kocic and G. Ladas, “Global Asymptotic Behavior of Nonlinear Difference Equation of Higher Order with Applications,” Kluwer Academic, Dordrecht, 1993.

