ABSTRACT

This paper is devoted to the study of a translation plane π(C) associated with a t-spread set C and its transposed t-spread set C ^t. In this paper, an explicit matrix form of the inverse of an isomorphism from a translation plane into another translation plane associated with t-spread sets is derived and proved that two translation planes associated with t-spread sets are isomorphic if and only if their corresponding transposed translation planes are isomorphic. Further, it is shown that the transpose of a flag-transitive plane is flag-transitive and derived a necessary and sufficient condition for a translation plane π(C) to be isomorphic to its transposed translation plane.

1. Introduction

A t-spread set C over a Galois field GF(q) where q is a power of a prime (see [1]), has become important since a translation plane π(C) of order q^t+1 can be constructed from it. The early study and use of t-spread sets can be found in the papers of Bruck and Bose [2,3]. Sherk [4] and Maduram [5] called t-spread sets as indicator sets and matrix representative sets respectively and studied them. Narayana Rao [6] has given a method of construction of t-spread sets. Several finite translation planes have been constructed using t-spread sets.

Maduram [7] considered C ^t, the t-spread set obtained by transposing the matrices of the t-spread set C and called the translation plane π(C ^t) associated with C ^t as the transposed translation plane of π(C). Maduram has proved that the translation complement of a translation plane and its transpose are isomorphic and exhibited the isomorphism explicitly ([7], Proposition 3). In the same paper Maduram considered eight classes of translation planes and shown that the transpose of a plane of a class belong to the same class ([7], Proposition 5).

In this paper (1) an explicit matrix form of the inverse of a given isomorphism T from a translation plane π(C₁) into another translation plane π(C₂) is derived, (2) the existence and an explicit form of an isomorphism corresponding to each isomorphism T: π(C₁) → π(C₂) is derived and the particular case when C₁ = C₂ = C is studied, (3) the one-one correspondence between the set G of all isomorphisms from π(C₁) to π(C₂) and the set G¢ of all isomorphisms from to 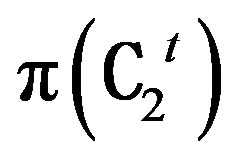is established and it is shown that this result strengthens to G @ G¢, in the particular case when C₁ = C₂ = C, where G and G¢ are translation complements of π(C) and its transposed translation plane π(C ^t) respectively, (4) it is shown that the transpose of a flag-transitive plane is a flag-transitive plane and (5) finally a necessary and sufficient condition for a translation plane π(C) to be isomorphic to its transposed translation plane π(C^t) is derived under a given set of conditions.

The results proved in (2) and (3) above are for isomorphisms between planes and in the particular case they turn out to be results related to the collineations of the planes and these results in the context of collineations coincide with the results in Proposition 3 of Maduram [7]. In this way the results proved in (2) and (3) are more general.

The result proved in (4) enables us to add the class of flag-transitive planes to the already existing eight classes of planes in Proposition 5 of Maduram [7].

2. Preliminaries and Some Results

In this section, we furnish general background necessary for this paper. Throughout this paper F, V(n,q), X^-t and π(C) denote the Galois field GF(q) of order q where q is the power of a prime p, the vector space of all n-tuples over GF(q), the transpose of the matrix X^-1 and a t-spread set over GF(q) respectively.

2.1. Andre’s Interpretation of Translation Planes [8]

Let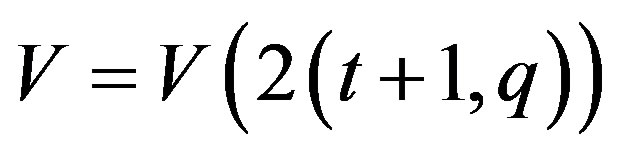. A set 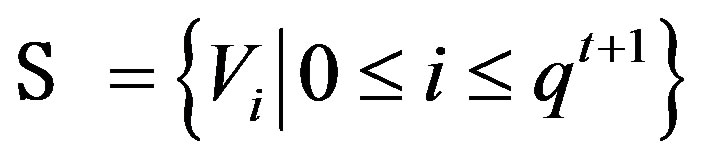of (t + 1)—dimensional subspaces of V is a spread in V if             V_i ∩ V_j = {0}, i ≠ j, 0 ≤ i, j ≤ q^t+1.

If π is an incidence structure with the vectors of V as points of π and the subspaces V_i (0 ≤ i ≤ q^t+1) of S together with their cosets in the group (V, +) as lines of π, with the inclusion as incidence relation then π is a translation plane of order q^t+1. A collineation of π fixing the point corresponding to the zero vector is a nonsingular linear transformation of V permuting the subspaces of the spread S  among themselves. The translation complement of a translation plane π is the group of all collineations which fix the point corresponding to the zero vector of π, i.e., the stabilizer of the origin.

2.2. The t-Spread Set and the Translation Plane Associated with It

Let t be a positive integer. A collection C of (t + 1) ´ (t + 1) matrices over F is a t-spread set [1] (matrix representative set) over F if it satisfies the following;

1) C contains q^t+1 matrices.

2) Zero and identity matrices of order t + 1 are elements of C.

3) If X, YÎ C, X ≠ Y, then determinant of (X - Y) ≠ 0.

From this it follows that each non-zero matrix of C is nonsingular.

Let F^t+1 be the vector space of (t + 1)—tuples over F. For each M Î C, define

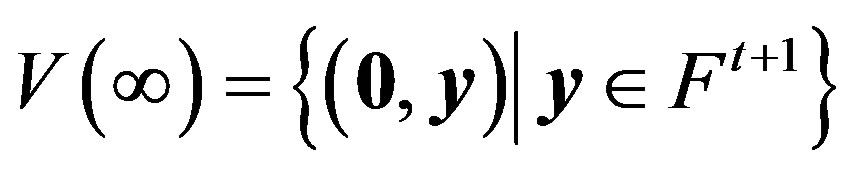
where 0 is the zero element of F^t+1 and

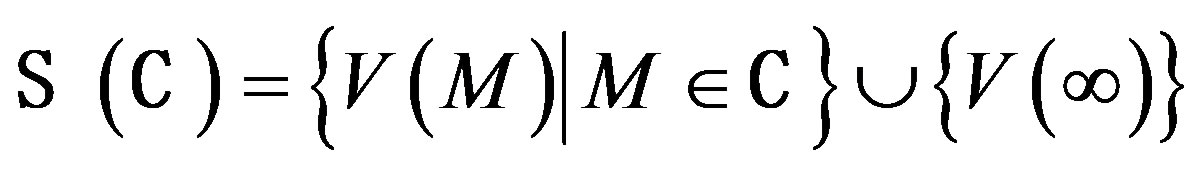
The members of S (C) are (t + 1)—dimensional subspaces of V = V(2(t + 1), q ) and S (C) is a spread in V, since C is a t-spread set over F.

Let π be the translation plane of order q^t+1 constructed from the spread S(C) as in 2.1. The translation plane π constructed via the t-spread set C in this way is denoted by π(C) and is called the translation plane associated with the t-spread set C. The t-spread set C is the matrix representative set of π(C) with the fundamental subspaces V(∞), V(0) and V(I), i.e., x = 0, y = 0 and y = x respectively.

The following is the result established by Maduram [5] on matrix representative sets.

Proposition 2.2.1: Matrix representative sets of any translation plane with the same fundamental subspaces are equivalent (conjugate).

2.3. Isomorphic Translation Planes and a Collineation

The discussion in this section is based on the work of Sherk [4] and Maduram [5].

Theorem 2.3.1 ([4], p. 217): Let C₁ and C₂ be t-spread sets over F. Let π(C₁) and π(C₂) be the translation planes associated with C₁ and C₂ respectively. The translation planes π(C₁) and π(C₂) are isomorphic if and only if there exists a nonsingular linear transformation, where A, B, C and D are matrices of order (t + 1) over F with the following properties:

Either a) C = 0, A is nonsingular and for each M Î C₁ there exists an N Î C ₂ such that 

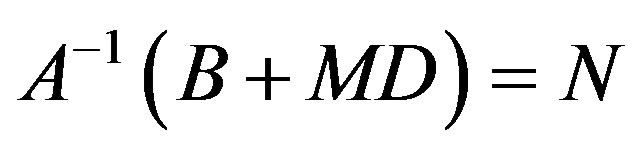
or b) C is nonsingular and there is a P Î C₂ such that C^-1D = P. Also there is a Q Î C₁ such that A + QC = 0. For each of the other matrices M Î C₁, A + MC is nonsingular and there exists an N Î C₂ such that

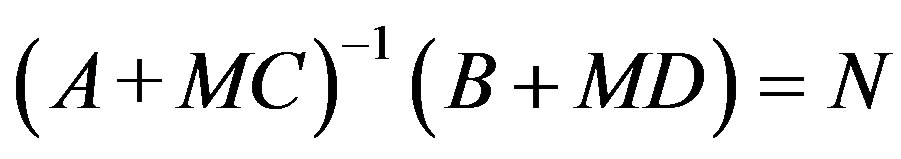
Taking C₁ = C₂ = C in the above theorem we get a necessary and sufficient condition for G to be a collineation of π(C).

Theorem 2.3.2: Let C be a t-spread set over F. A nonsingular linear transformation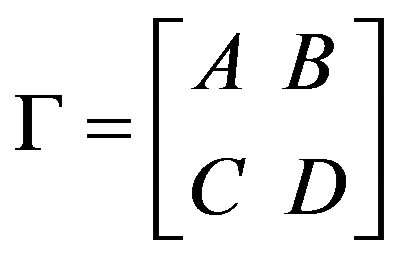, where A, B, C and D are matrices of order t + 1 over F, induces a collineation in π(C) if and only if the following properties hold:

Either a) C = 0, A is nonsingular and for each M Î C there exists an N Î C such that

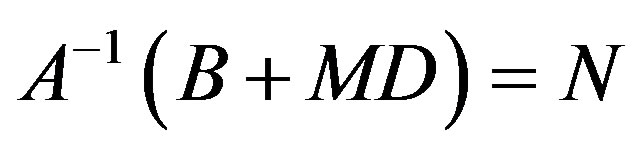
or b) C is nonsingular and there is a P Î C such that C^-1D = P. Also there is a Q Î C such that A + QC = 0. For each of the other matrices M Î C, A + MC is nonsingular and there exists an N Î C such that

The following is the relation between the matrix representative sets of isomorphic translation planes:

Proposition 2.3.3 [5]: If two matrix representative sets are equivalent then the corresponding translation planes are isomorphic. Conversely, isomorphic translation planes have equivalent matrix representative sets.

The matrix representative sets of a translation plane and collineations are related in the following way:

Proposition 2.3.4 [5]: In a translation plane there exists a collineation, mapping three given lines through a point onto another three such lines if and only if the matrix representative sets corresponding to these two sets of fundamental lines are equivalent.

2.4. Transposed Translation Planes

Maduram [7] considered the transposed t-spread set (matrix representative set) C ^t = {M^t|M Î C} of a given t-spread set C over F and shown that C^t is also a t-spread set [7, p. 266]. Let

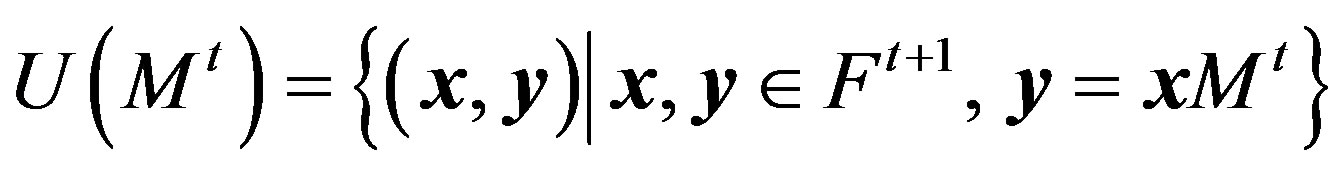
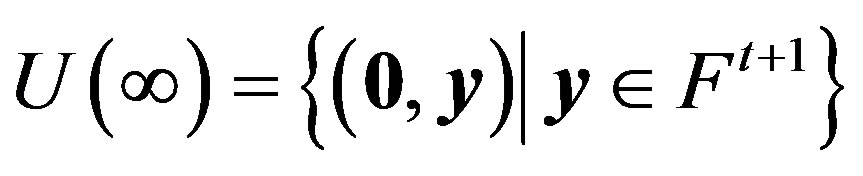and

Clearly S (C ^t) is a spread in V.

Let π(C ^t) be the translation plane of order q^t+1 constructed from the spread S (C ^t) as in 2.1. It is the translation plane associated with C ^t and π(C ^t) is said to be the transposed translation plane of π(C). Maduram [7] studied various properties of transposed translation planes.

The following are important results obtained by Maduram on transposed translation planes.

Proposition 2.4.1 ([7] Proposition 3, p. 267): The translation complement of any translation plane is isomorphic to that of its transpose.

Maduram explicitly had given the following isomorphism ψ ([7], p. 268) from the translation complement of π(C) onto the translation complement of its transposed translation plane S (C ^t):

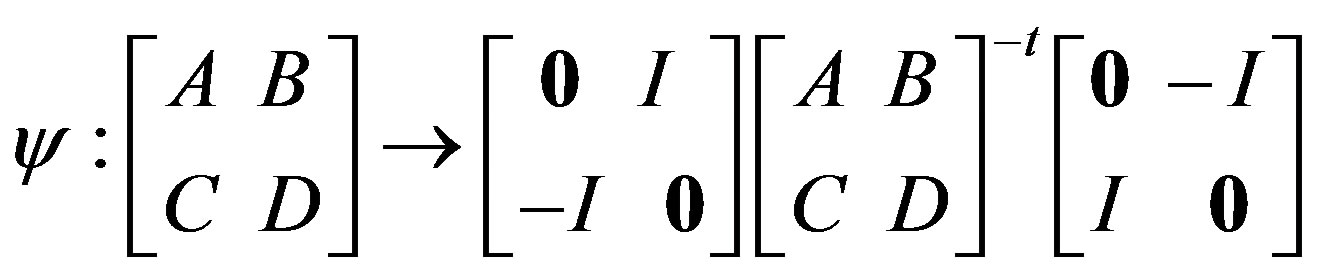
Proposition 2.4.2 ([7] Proposition 5, p. 269): The transpose of the following classes of planes belong to the same class: a) Desarguesian planes, b) near—field planes, c)

semi-field planes, d) generalized Hall planes, e) Luneburg planes, f) Bol planes, g) generalized Andre planes, and h) C-planes.

2.5. Flag-Transitive Planes

A finite affine plane π is a flag-transitive plane if it admits a collineation group that is transitive on the incident point-line pairs or flags of π [9]. Wagner [10] has shown that π is a translation plane so that its order is some positive integral power of prime.

The translation plane π = π(C), of order q^t+1, associated with the t-spread set C over F is flag-transitive if there exists a collineation group which permutes the subspaces of the spread S (C) in V.

3. Explicit Matrix Form of the Inverse of an Isomorphism

Let C₁ and C₂ be t-spread sets over F and π(C₁) and π(C₂) respectively be the translation planes associated with them. If T is the matrix form of an isomorphism from π(C₁) to π(C₂), then an explicit form of the isomorphism T^-1 is given in the following theorem:

Theorem 3.1: If be an isomorphism from

π(C₁) to π(C₂) then the explicit form of the isomorphism T^-1 from π(C₂) to π(C₁), is given below.

If C = 0, then A and D are nonsingular and

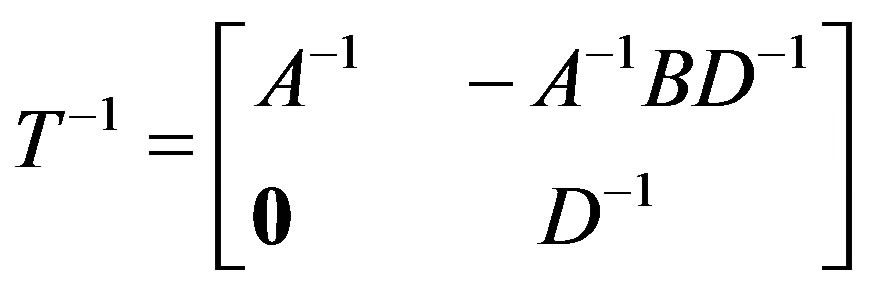(3.1.1)

If C is nonsingular then either A = 0 or A is nonsingular and either D = 0 or D is nonsingular. Furthera) If A = D = 0, then

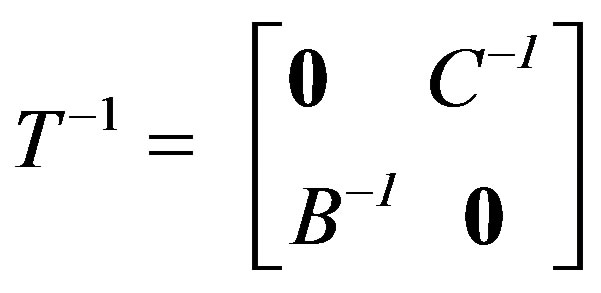(3.1.2)

b) If A is nonsingular, then C^-1D - A^-1B is nonsingular and

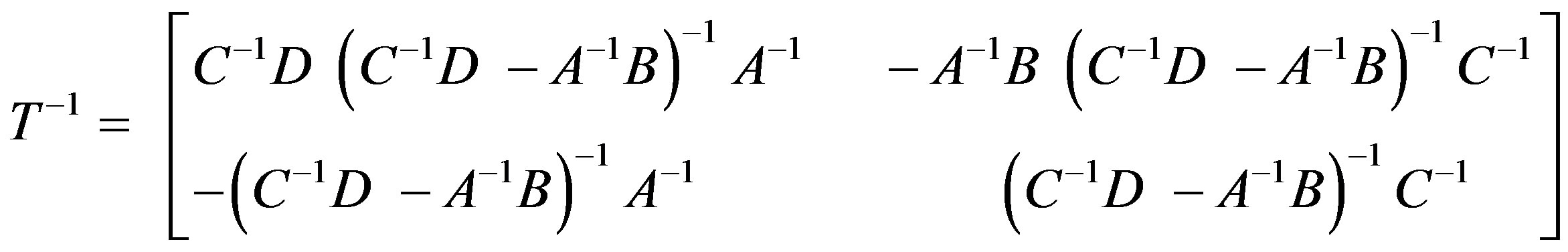(3.1.3)

c) If D is nonsingular then AC^-1 - BD^-1 is nonsingular and

(3.1.4)

Proof: If C = 0 then A and D must be nonsingular (since T is nonsingular) and the result follows trivially.

Let C be nonsingular. Since T is an isomorphism from π(C₁) to π(C₂) the following hold:

There exists matrices P Î C₂, Q Î C₁ such that C^-1D = P, A + QC = 0, i.e., Q = -AC^-1 and for each M ≠ Q in C₁, A + MC is nonsingular and there is an N ≠ P in C₂ such that (A + MC)^-1(B + MD) = N. Now we can have either P = 0 or P ≠ 0 and Q = 0 or Q ≠ 0. If P = 0 then D = 0. If P ≠ 0 in C₂, then P is nonsingular (since C₂ is a t-spread set) and D is nonsingular. By a similar argument if Q = 0 then A = 0, and if Q ≠ 0 then A is nonsingular. Thus, we get either A = 0 or A is nonsingular and D = 0 or D is nonsingular.

a) Let A = 0, D = 0 in T. Then B must be nonsingular (since T is nonsingular) and the result follows trivially.

b) Let A be nonsingular. Then Q is nonsingular in C₁ and hence Q ≠ 0. Thus we can take M = 0 and there is a matrix N ≠ P in C₂ such that A^-1B = N. Since C₂ is a t-spread set, P - N is nonsingular. i.e., C^-1D - A^-1B is nonsingular.

Let. Now. This in turn implies AX + BZ = I, CX + DZ = 0; AY + BW = 0 and CY + DW = I. Solving for X, Y we get X = -C^-1DZ, Y = -A^-1BW. Finally we get Z = -(C^-1D - A^-1B)^-1A-1, W = (C^-1D - A^-1B)^-1C-1. There by X = C^-1D(C^-1D - A^-1B)^-1A-1, and Y = -A^-1B(C^-1D - A^-1B)^-1C-1. Thus

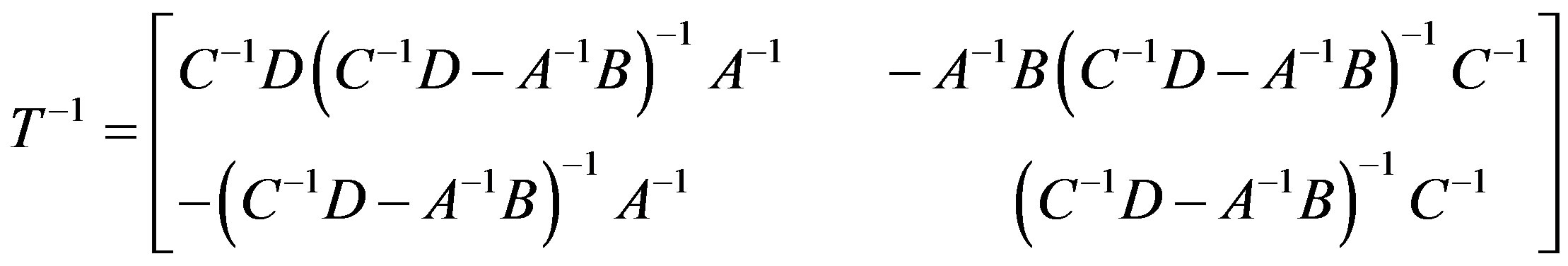
c) Let D be nonsingular then P is nonsingular in C₂ and hence P ≠ 0. Thus, we can take N = 0 and there is a matrix M ≠ Q in C₁ such that (A + MC)^-1(B + MD) = 0, implying (B + MD) = 0 i.e., M = -BD^-1. Since C₁ is a t-spread set, Q - M is nonsingular, i.e., AC^-1 - BD^-1 is nonsingular. Taking 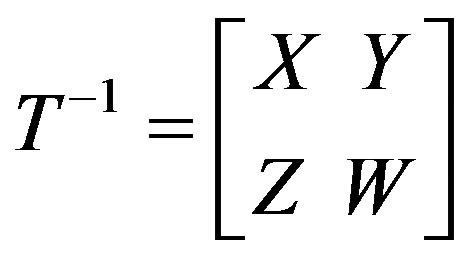and considering

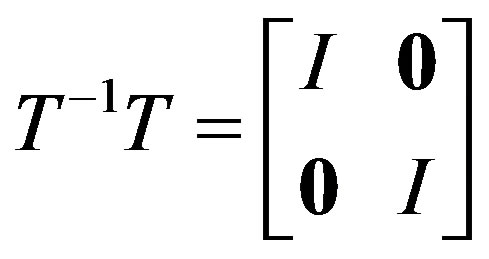, we get XA + YC = I, XB + YD = 0ZA + WC = 0 and ZB + WD = I. Solving for Y, W, we get Y = -XBD^-1, W = -ZAC^-1. Finally, we get

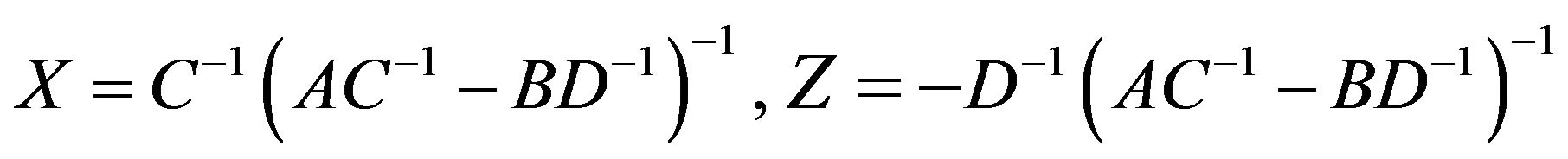
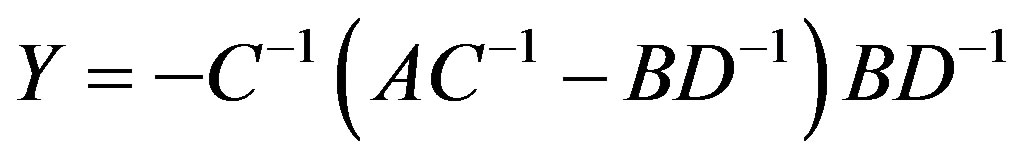
and.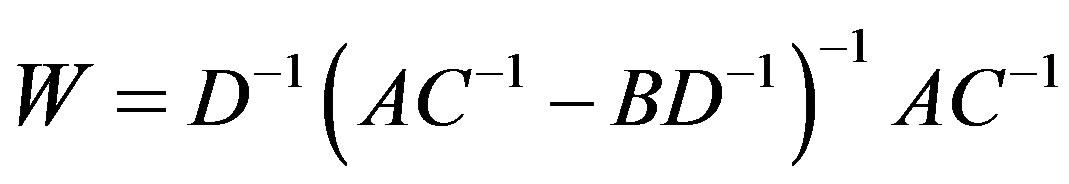

Thus,

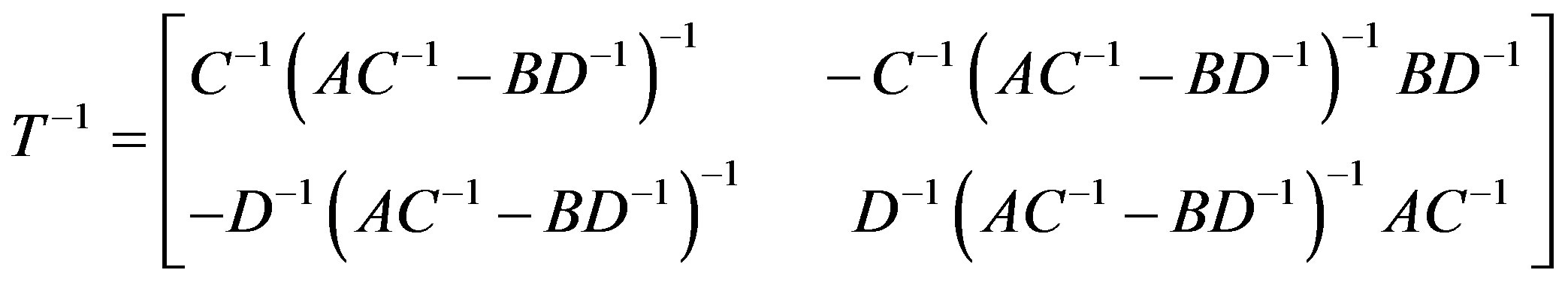
Hence the theorem.

Remark 3.2: a) The form of T^-1 given in (3.1.3) holds in the case either D = 0 or D is nonsingular when A is nonsingular b) The form of T^-1 given in (3.1.4) holds in the case either A = 0 or A is nonsingular when D is nonsingular c) If A and D are both nonsingular in T, then

Corollary 3.3: Let 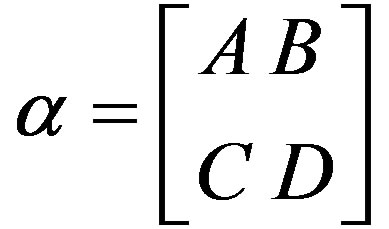be a collineation of a translation plane π(C). The explicit matrix form of the collineation α^-1 is given below:

If C = 0, then A and D are nonsingular and α^-1 is given by (3.1.1).

If C is nonsingular, then either A = 0 or A is nonsingular and either D = 0 or D is nonsingular a) If A = D = 0, then a^-1 is given by (3.1.2), b) If A is nonsingular, then C^-1D - A^-1B is nonsingular and α^-1 is given by (3.1.3), c)

If D is nonsingular, then AC^-1 - BD^-1 is nonsingular and α^-1 is given by (3.1.4).

Proof: Proof follows from the above theorem with C₁ = C₂ = C.          

4. Isomorphic Planes and Their Transposed Planes

In this section, we prove that two translation planes are isomorphic if and only if the corresponding transposed translation planes are isomorphic. We start with the following definition:

Definition 4.1: Let T be an isomorphism from π(C₁) into π(C₂) and S be an isomorphism from 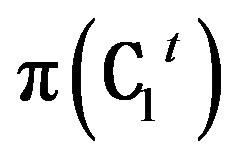to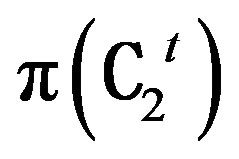. We say that T and S have the same action if, either

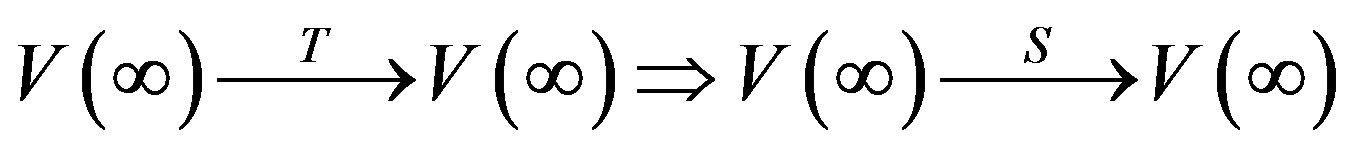
and for each M Î C₁, there exists an N Î C₂ such that

.

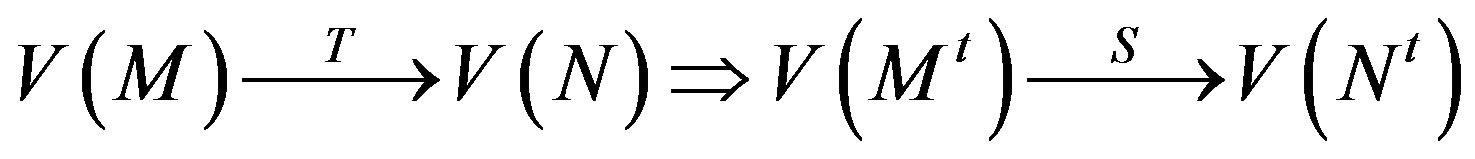or there exist matrices Q Î C₁ and P Î C₂ such that

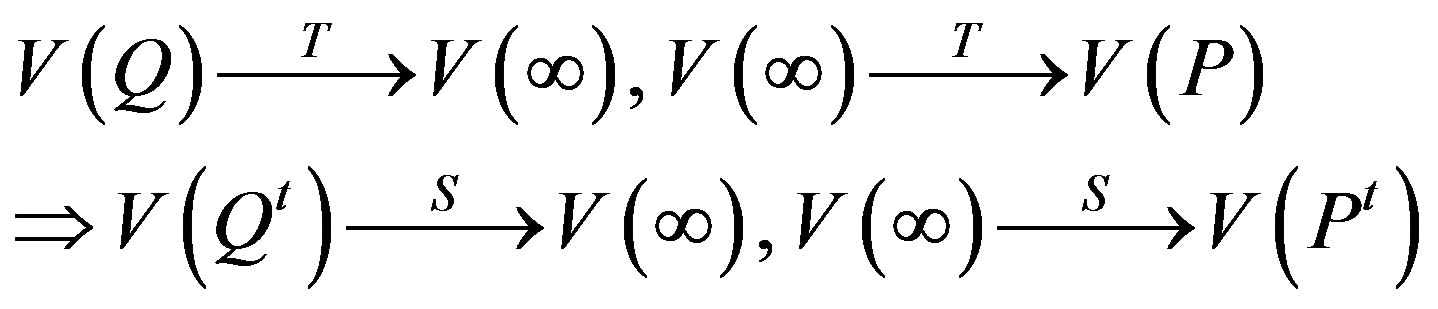
and for each M Î C₁ (M ≠ Q) there exists an N Î C₂ such that

.

The following Theorem proves that for each isomorphism T from π(C₁) to π(C₂) there exists an isomorphism T¢ from to such that T and T¢ have the same action. Further, the explicit matrix form of T¢ is derived and the particular case when C₁ = C₂ = C is studied.

Theorem 4.2: If 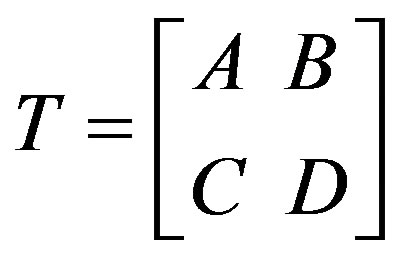is an isomorphism from the translation plane π(C₁) to the translation plane π(C₂)then there exists an isomorphism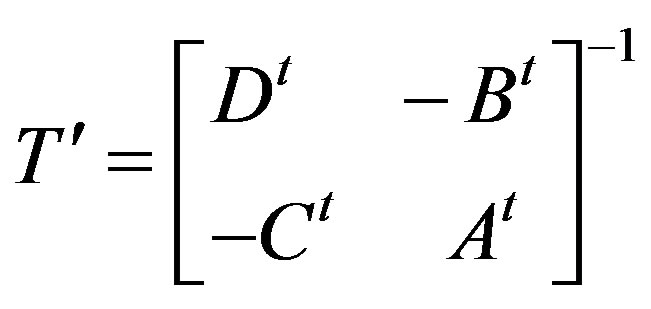

from 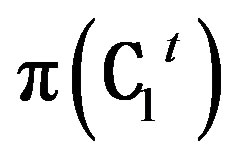to. Further, the action of T¢ from to 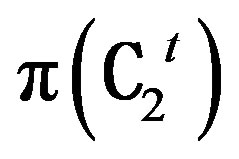is same as the action of T from π(C₁) to π(C₂).

Proof: Let 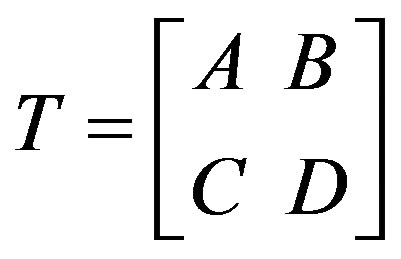be an isomorphism from π(C₁)

to π(C₂).

Case a): Let C = 0 in T. Then A and D must be nonsingular. Since T is an isomorphism for each M Î C₁ there exists an N Î C₂ such that

(4.2.1)

Notice that

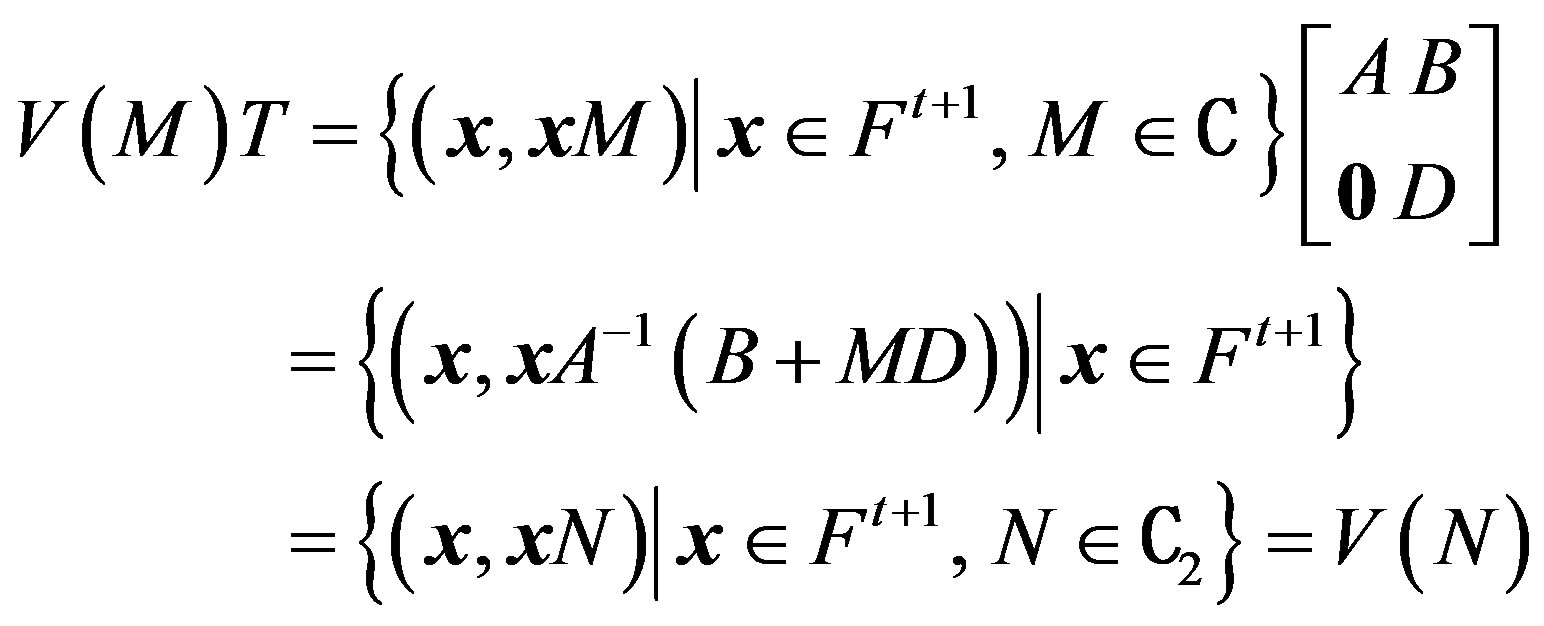
Thus,.

Transposing (4.2.1), we get (B^t + D^tM^t)A^-t = N^t and

(4.2.2)

This shows that for each M^t Î there exists an N^t Î such that (4.2.2) holds. Therefore,

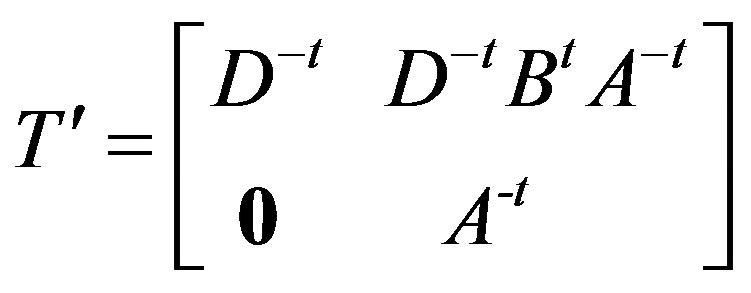
is an isomorphism from 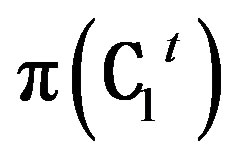to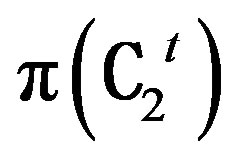. As before it is easy to see that

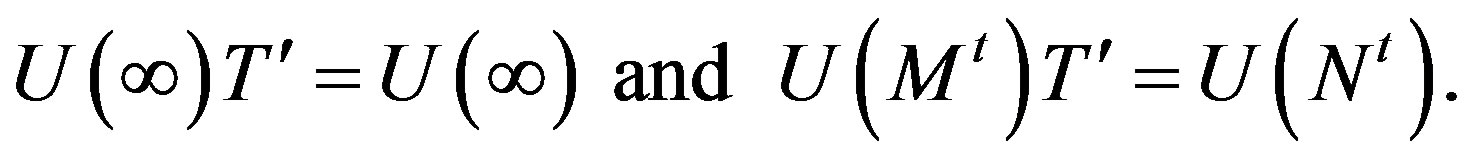
Thus,.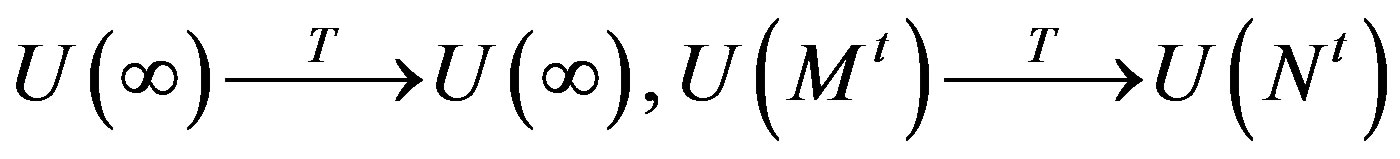

It may be seen that

and T and T' have the same action.

Case b): Let C be nonsingular in T. Since T is an isomorphism, the following hold:

There is a P Î C₂ such that 

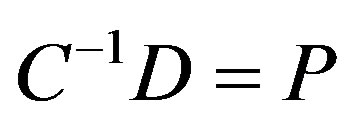(4.2.3)

There is a Q Î C₁ such that

(4.2.4)

For each M (≠ Q) in C₁, A + MC is nonsingular and there is an N (≠ P) in C₂ such that

(4.2.5)

From the above, we see

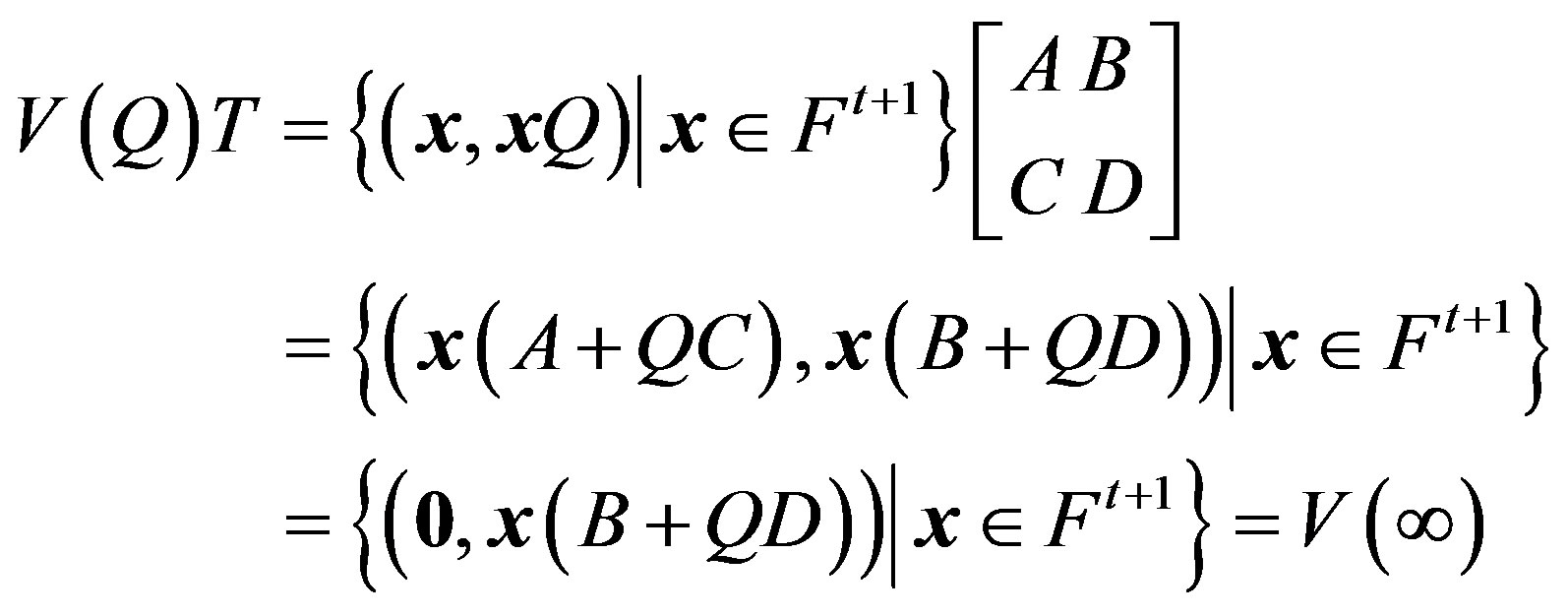
Thus, , and .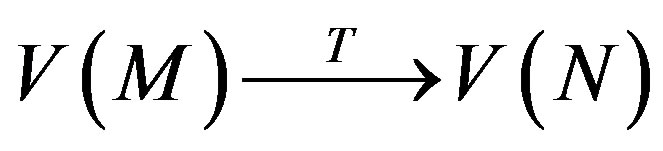

Transposing (4.2.3), we get D^tC^-t = P^t, i.e., D^t + P^t(-C^t) = 0.Thus there is a P^t Î such that

(4.2.6)

Transposing (4.2.4) we get Q^t = -C^-tA^t = (-C^t)^-1A^t. Thus there exists Q^t Î 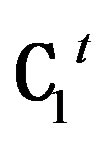such that

(4.2.7)

Transposing (4.2.5) and simplifying we get (D^t - N^t C^t)M^t = N^tA^t - B^t. Notice that N, P = C^-1D Î C₂, N ≠ P. Since C₂ is a t-spread set, the difference of any two distinct matrices of C₂ is nonsingular. Hence N-C^-1D is nonsingular. This forces D - CN is nonsingular. Hence (D - CN)^t  = (D^t - N^tC^t) is nonsingular. Thus, for each N^t (≠ P^t) in there exists a M^t (≠ Q^t) in 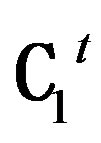such that

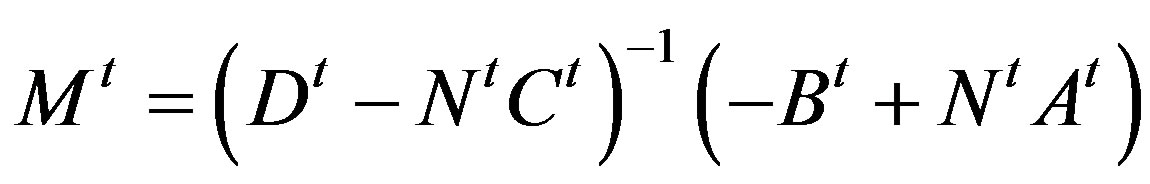(4.2.8)

From (4.2.6), (4.2.7) and (4.2.8), it follows that

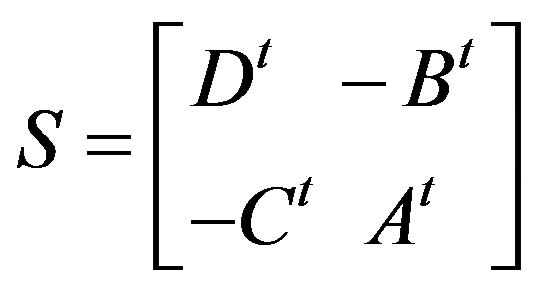is an isomorphism from 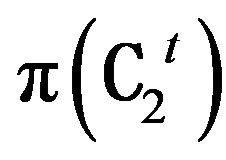to

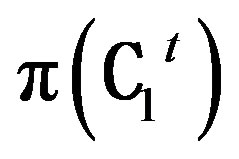and

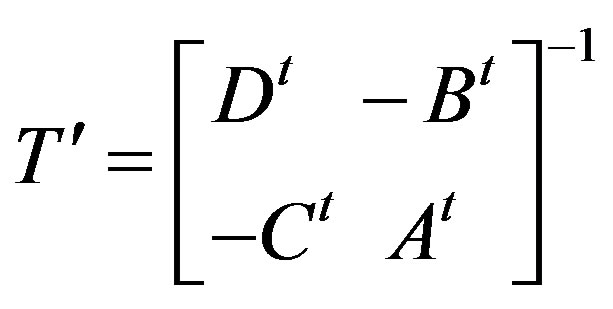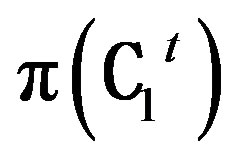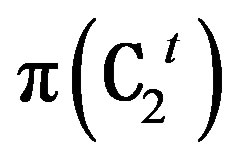Since S is an isomorphism, S is nonsingular and hence S^-1 exists. Let T' = S^-1 then is an isomorphism from to and

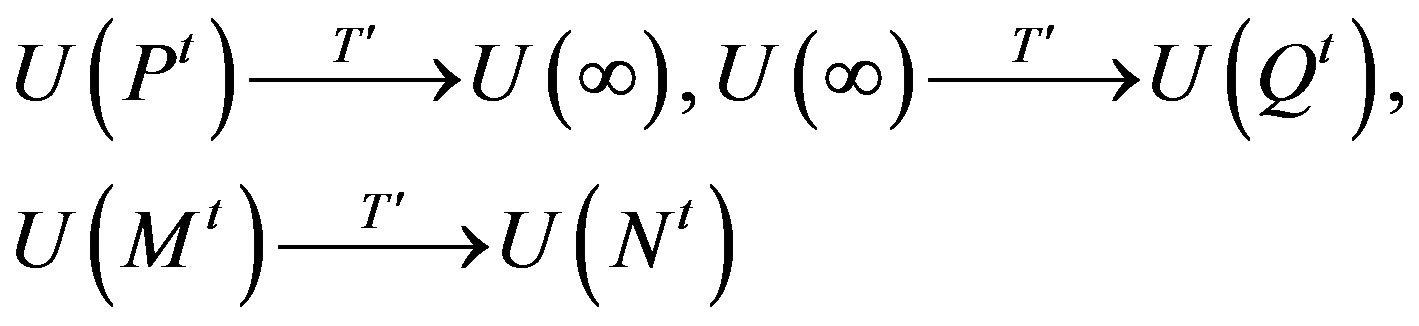
It may be readily seen that T and T¢ have the same action.

Hence the theorem.

Note 4.3: It may be seen that

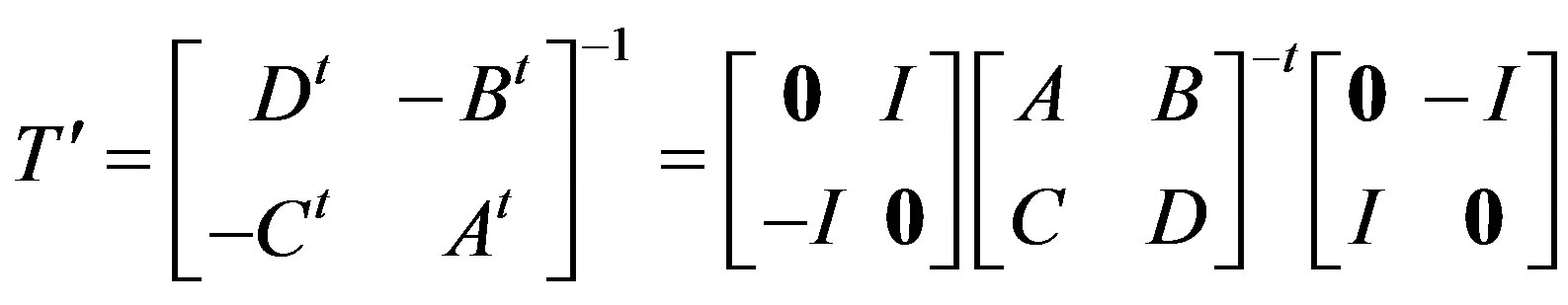
Corollary 4.4: Let C be a t-spread set. If 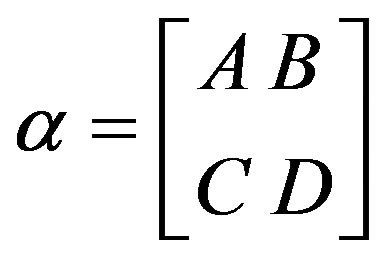is a collineation of the translation plane π(C), then

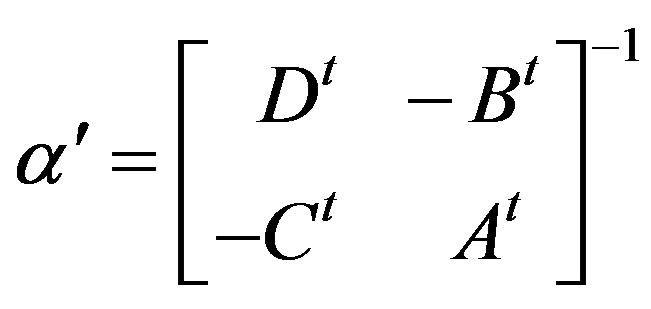is a collineation of the transposed translation plane π(C ^t). Further, α and α¢ have the same action on the subspaces of the underlying spreads of π(C) and π(C ^t).

Proof: Proof follows from the Theorem 4.2 when C₁ = C₂ = C.

We have derived this explicit form in the context of isomorphisms, where as Maduram [7] has derived in the context of collineations. In Theorem 4.2 we have in fact proved the following result.

Theorem 4.5: Two translation planes are isomorphic if and only if their corresponding transposed translation planes are isomorphic.

5. A Study of Isomorphisms in a Translation Plane and in the Corresponding Transposed Translation Plane

In this section, we prove that G, the set of all isomorphisms from π(C₁) to π(C₂) and G¢, the set of all isomorphisms from to are in one-one correspondence. In the particular case when C₁ = C₂ = C, we prove that G @ G¢

Theorem 5.1: If G and G¢ are the sets of all isomorphisms from π(C₁) to π(C₂) and to 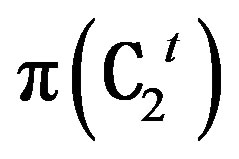respectively, then the map ψ: G→G¢ defined by

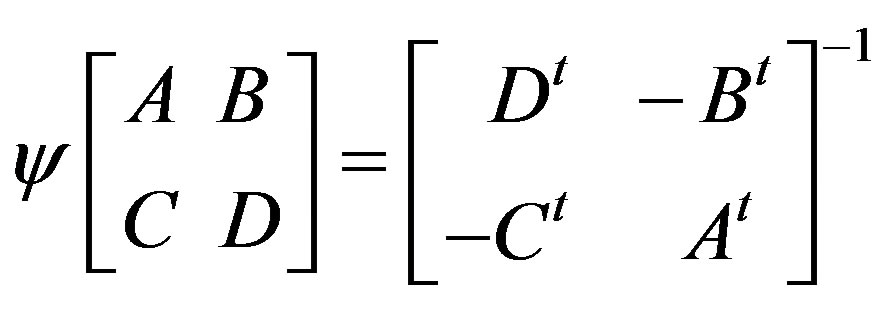
is bijective.

Proof: a) Let, 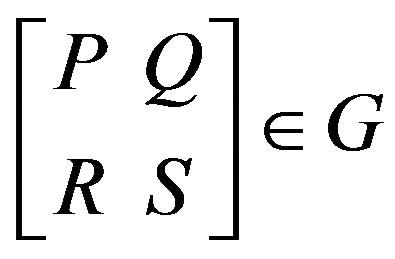and

.

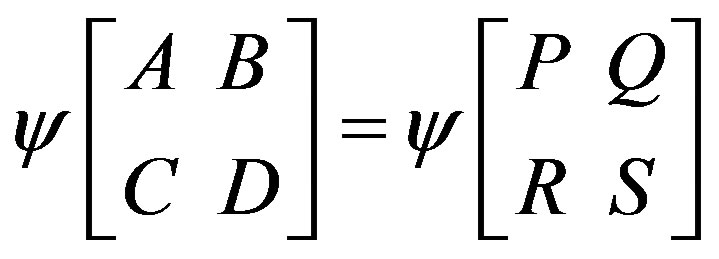A straight forward computation shows that D^t = S^t, -B^t = -Q^t, -C^t = -R^t and A^t = P^t. This in turn implies A = P, B = Q, C = R and D = S. It now follows that ψ is one-one.

b) Let 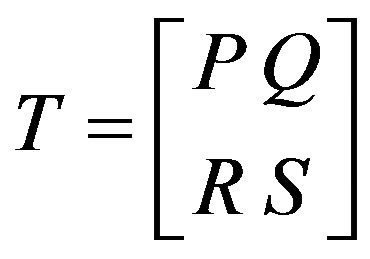be any isomorphism from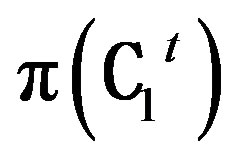

to 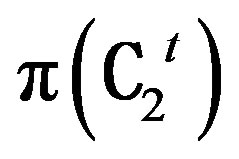i.e., T Î G¢. By Theorem 4.2, there exists an isomorphism from π(C₁) to π(C₂).

Note that T¢ Î G. To prove ψ is onto, we prove ψ(T') = T. This is done in the following different cases.

Case i): Let R = 0 in T. Then by Theorem 3.1, P and S are nonsingular and. Now there exist 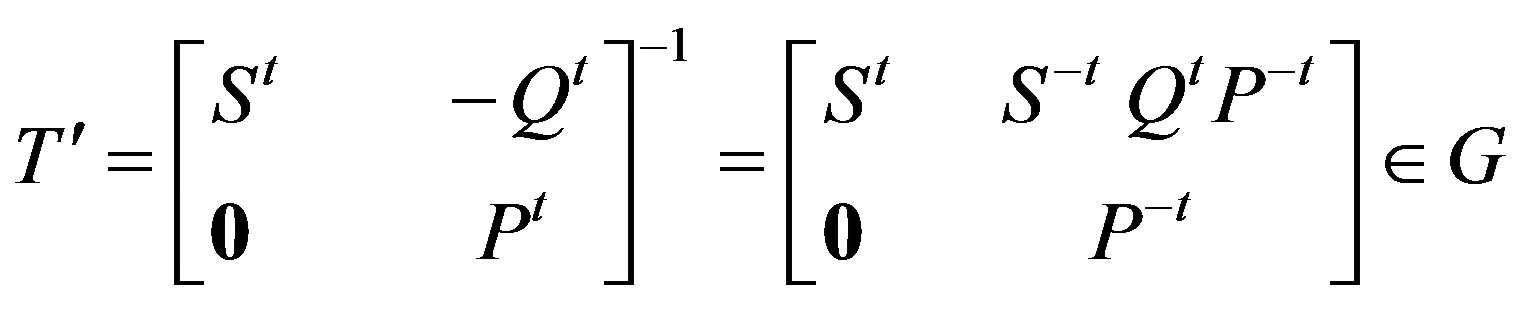and

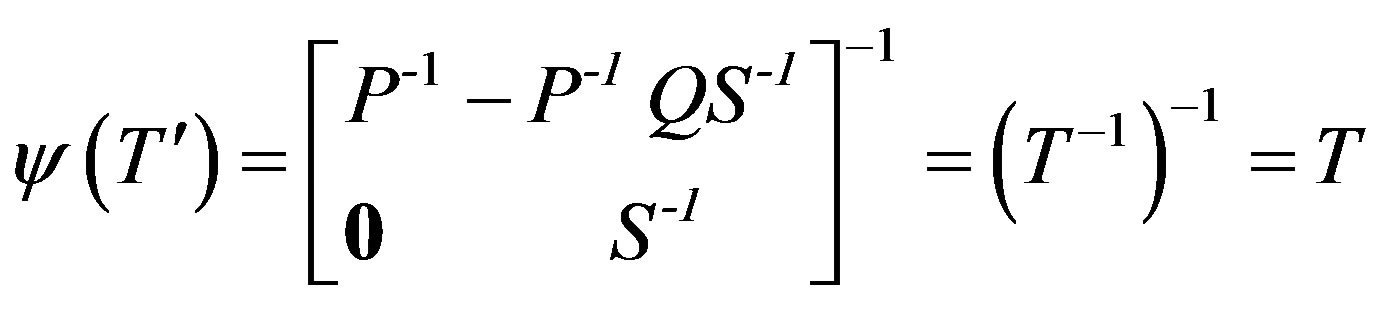
Case ii): Let R be nonsingular in T. Then by Theorem 3.1, we have either P = 0 or P is nonsingular and either S = 0 or S is nonsingular. Now the following cases arise.

a) If P = S = 0 in T, then by Theorem 3.1,

.

Now there exists

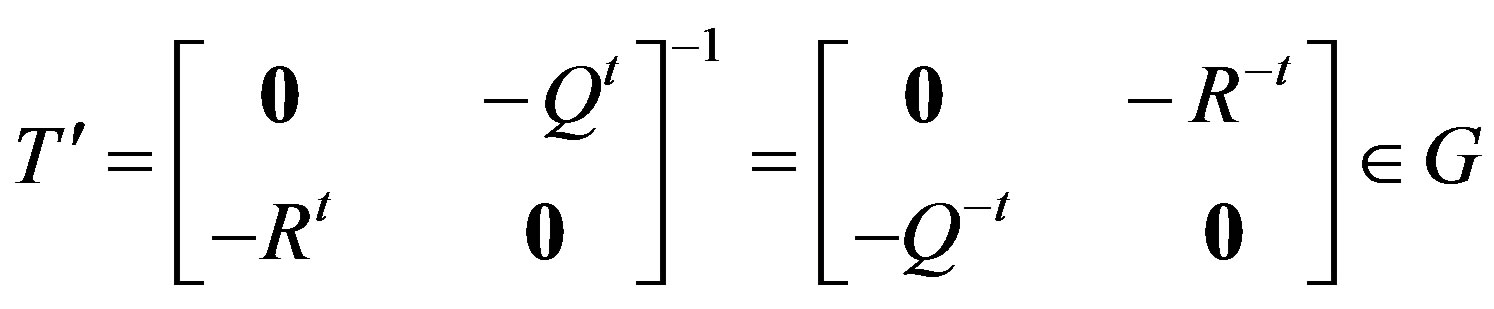
and

b) If P is nonsingular in T, then by (b) of Theorem 3.1, R^-1S - P^-1Q is nonsingular and

.

Now there exists a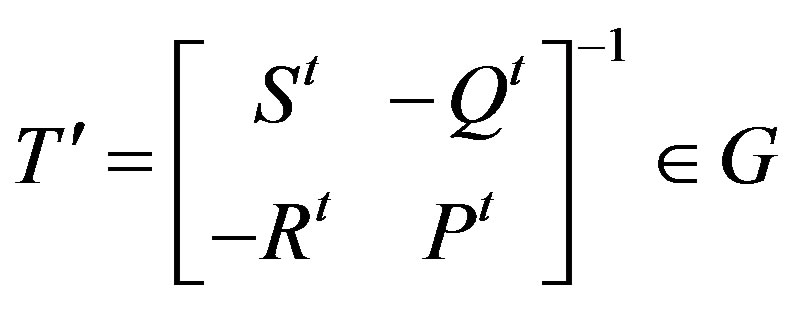. Clearly P^t is nonsingular and (R^-1S - P^-1Q)^t = S^tR^-t - Q^tP^-t is nonsingular. There by -S^tR^-t + Q^tP^-t is nonsingular. By (c) of Theorem 3.1

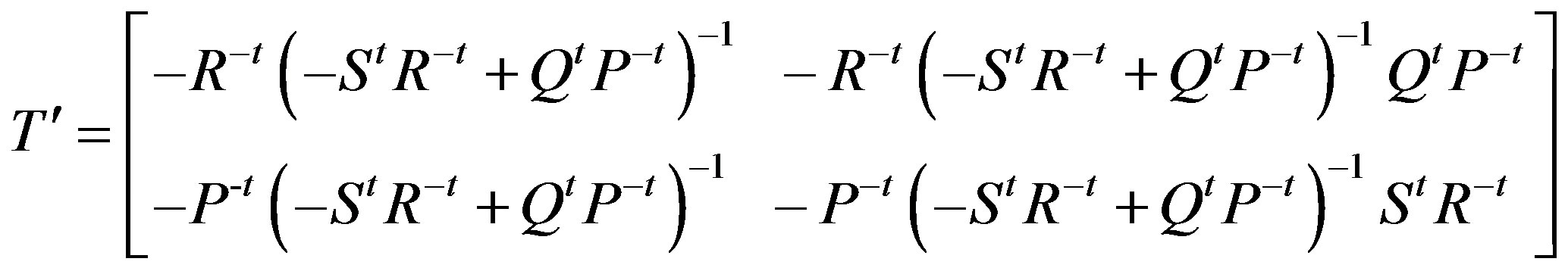
and

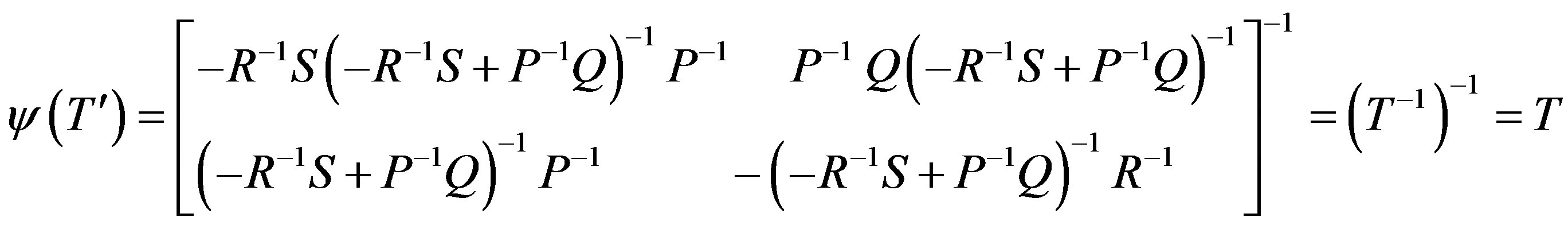
c) If S is nonsingular in T, then by (c) of Theorem 3.1, PR^-1 - QS^-1 is nonsingular and

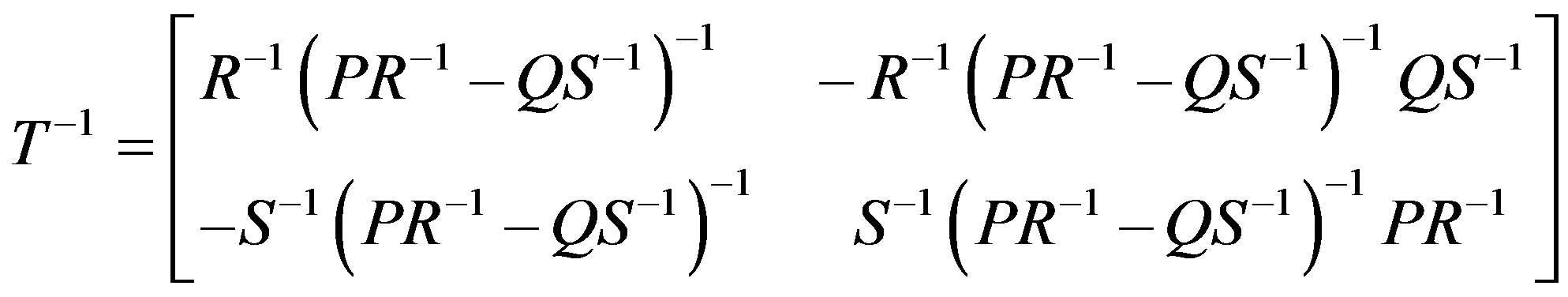
Now for this T, there exists a.

We readily see that S^t is nonsingular, (PR^-1 - QS^-1)^t = R^-tP^t - S^-tQ^t is nonsingular and -R^-t P^t + S^-t Q^t is nonsingular. By (b) of Theorem 3.1,

and

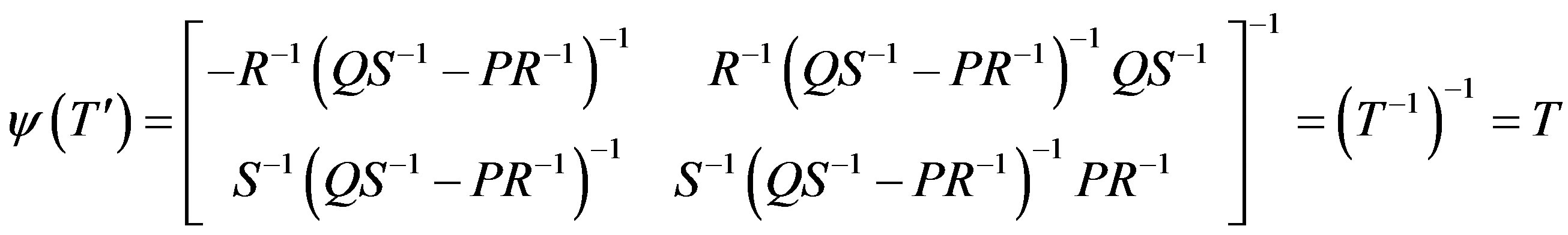
Combining all the cases above, we have shown that for any T Î G¢ there exists a T¢ Î G such that ψ(T¢) = T. This shows that T is onto. Thus, ψ is bijective.

Hence the theorem.

In the particular case when C₁ = C₂ = C, G and G¢ turns out to be the translation complements of π(C) and π(C ^t) respectively. The bijection ψ: G→G¢ strengthens to be an isomorphism and thus proves the result of Maduram ([7] Proposition 3, p. 267) i.e., the translation complement of a given translation plane and that of its transpose are isomorphic.

Theorem 5.2: If G and G¢ are the translation complements of π(C) and π(C ^t) respectively, then G is isomorphic to G¢ and the isomorphism from G onto G¢ is given by ψ where

Proof: In the above Theorem 4.1, let us take C₁ = C₂ = C. Then G and G¢ will become the groups of all collineations of π(C) and π(C ^t) respectively, i.e., G and G¢ will be the translation complements of π(C ) and π(C ^t). Define a map ψ: G → G¢ by

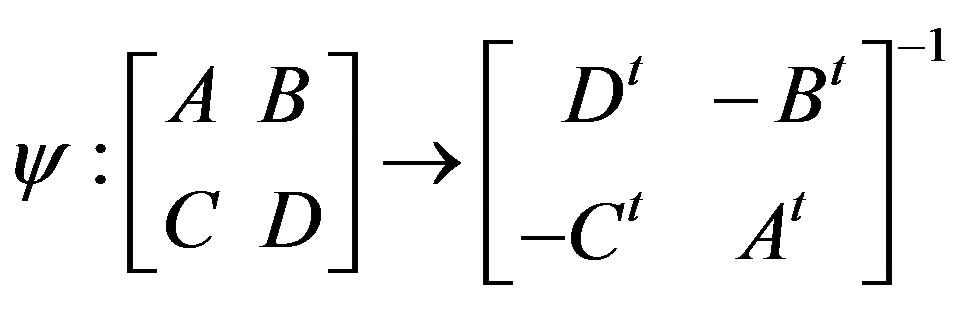
Clearly this map ψ is bijective (by Theorem 5.1). Let αβ Î G and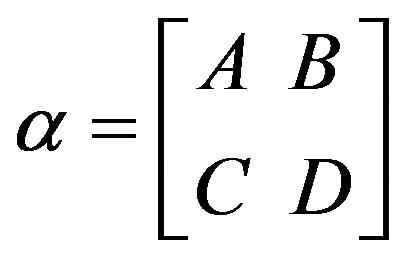,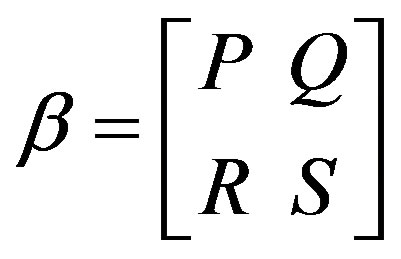. Now

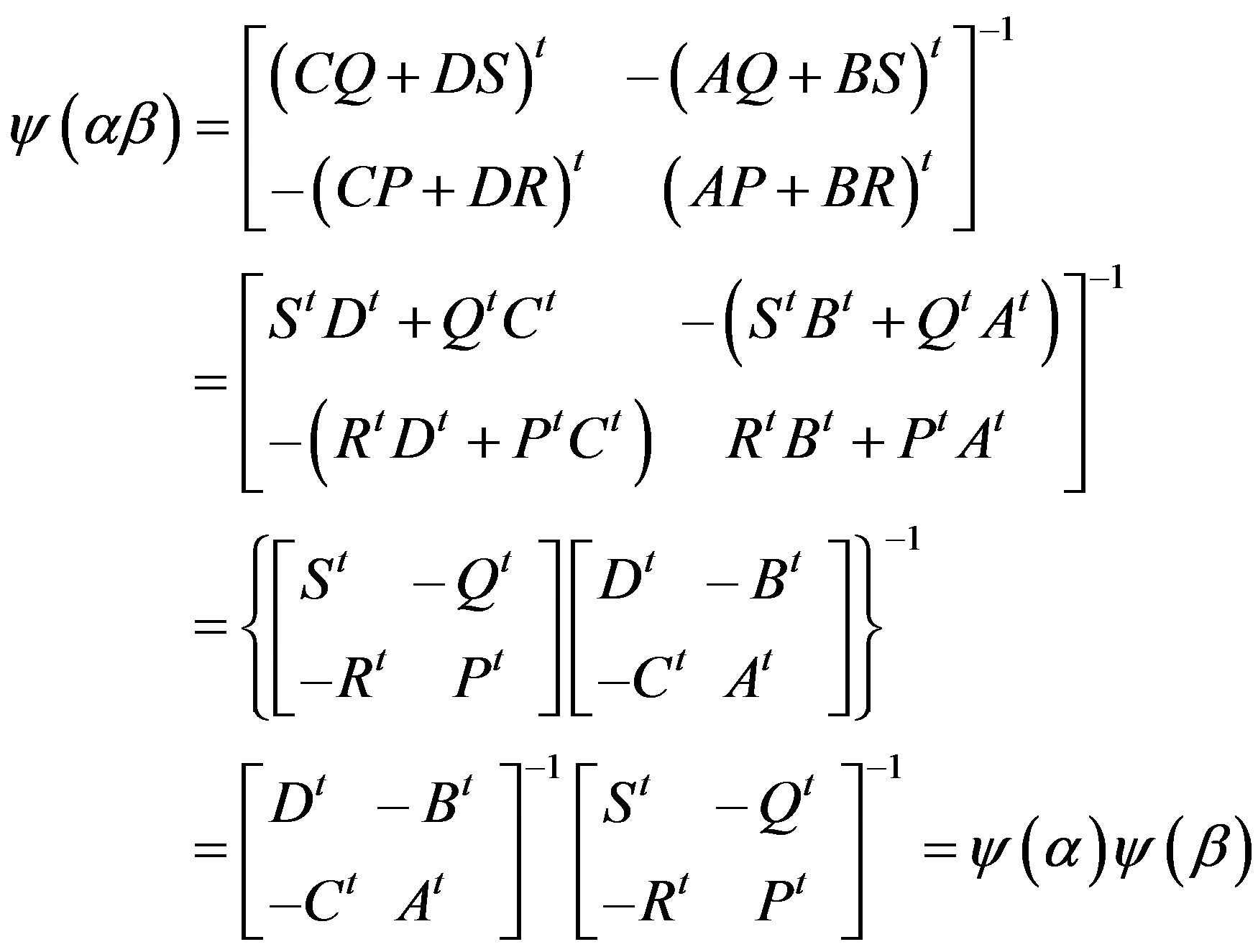
Thus, ψ is a homomorphism and ψ: G→G¢ is an isomorphism. Hence G @ G¢.

Hence the theorem.

6. On the Transpose of a Flag-Transitive Plane

In this section we prove that the transpose of a flag-transitive plane is also flag-transitive.

Theorem 6.1: The transpose of a flag-transitive plane is flag-transitive.

Proof: Let C be a t-spread set over F. Then S (C) = {V(M)|M Î C } {V(∞)} is a spread in V = V(2(t + 1),q). Let π(C) be the flag-transitive plane of order q^t+1 and G be its translation complement. Since π(C) is flag-transitive, it admits a collineation group H Í G which is transitive on the members of S (C). Consider C^t, the transpose of the t-spread set of C. Then S (C^t) is a spread in V. Let π(C^t) be the transposed translation plane of π(C) and G¢ be its translation complement. The aim of this result is to prove π(C^t) is flag-transitive. By Theorem 5.2, G @ G¢ and the isomorphism ψ: G→G¢ is given explicitly as

Clearly, H¢ = ψ(H) is a subgroup of G¢. By the Corollary 4.5, H and H¢ have the same action on the members of S (C) and S (C ^t) respectively. Since H is transitive on the members of S (C), H¢ is also transitive on the members of S (C ^t). This shows that π(C ^t) is flag-transitive.

Hence the theorem.

Maduram [7] considered eight classes of translation planes and shown that the transpose of a plane of a class belong to the same class. By the above theorem the class of flag-transitive planes is to be annexed to the already existing eight classes in the proposition 5 of Maduram [7].

7. Existence or otherwise of an isomorphism from π(C^t) to π(C)

In this section we derive a necessary and sufficient condition for π(C^t) to be isomorphic to π(C) under a given set of conditions.

Let X, Y Î C. We say that V(X) and V(Y) are companions if every collineation of π(C) that fixes V(X) also fixes V(Y) alone and if every collineation of π(C) that fixes V(Y) also fixes V(X) alone.

Theorem 7.1: Suppose that i) Every collineation of π(C) that fixes V(∞) also fixes V(0) and no others and ii) π(C) has a collineation d that flips V(∞) and V(0). Then a) V(∞) and V(0) are companions b) H, the collineation group that fixes V(∞) and V(0), partitions the members of S other than V(∞) and V(0) into orbits of length greater than 1, c) The t-spread sets of C·P^-1 and C·Q^-1 are equivalent if and only if V(P) and V(Q) belong to the same orbit of S  - {V(∞), V(0)} under H.

Proof: a) Given that no collineation of π(C) moves V(0) while fixing V(∞). Assume that π(C) has a collineation a that fixes V(0) and moves V(∞). Then d⁻¹ad fixes V(∞) and moves V(0), a contradiction. This proves that every collineation that fixes V(0) also fixes V(∞) and no others. From this it follows that V(∞) and V(0) are companions.

b) Clearly, H fixes V(∞) and V(0) and no others. The result (b) follows trivially.

c) If V(P) and V(Q) belong to the same orbit of S - {V(∞), V(0)} under H then there exists a collineation b Î H such that

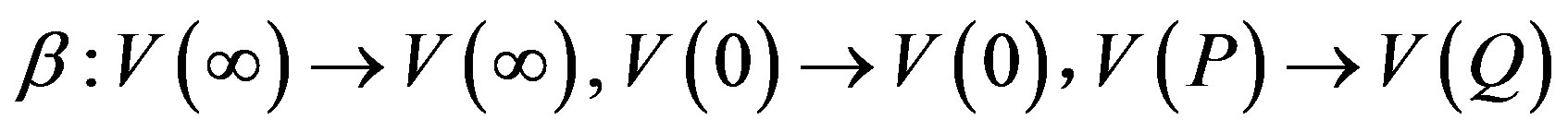
By Proposition 2.3.4, the matrix representative set of π(C) corresponding to the fundamental subspaces V(∞), V(0), V(P) is equivalent to the matrix representative sets of π(C) corresponding to the fundamental subspaces V(∞), V(0), V(Q) i.e., C·P^-1 is equivalent to C·Q^-1.

Conversely, suppose C·P^-1 is equivalent to C·Q^-1. By proposition 2.3.4, there exists a collineation a mapping V(∞), V(0) and V(P) onto V(∞), V(0) and V(Q) respectively. This means that a Î H and a sends V(P) onto V(Q). Thus V(P) and V(Q) belong to the same orbit of  S -{V(∞), V(0)} under H.

Hence the result.

Theorem 7.2: Suppose that i) every collineation of π(C) that fixes V(∞) also fixes V(0) and no others ii) π(C) has a collineation d that flips V(∞) and V(0) and iii) H is the group of collineation that fixes both V(∞) and V(0). Then π(C ^t) @ π(C) if and only if C ^t is equivalent to C·X^-1 for some XÎ C where V(X) is any one member taken from the orbits of S - {V(∞), V(0)} under H.

Proof: From the above theorem, V(∞) and V(0) are companions and H partitions the members of S -{V(∞), V(0)}into orbits of length greater than 1.

Suppose C ^t is equivalent to C·X^-1 for some X Î C, where V(X) is any one member taken from the orbits of S -{V(∞), V(0)} under H. Notice that C·X^-1 is a matrix representative set of π(C) with fundamental subspaces V(∞), V(0) and V(X). By Proposition 2.3.3, the corresponding translation planes associated with C ^t and C·X^-1

are isomorphic. Thus π(C ^t) @ π(C).

Conversely, suppose π(C^t) @ π(C). Let f be the isomorphism from π(C ^t) to π(C). By Corollary 4.4, for each collineation a of π(C), there is a collineation a¢ of π(C ^t) such that a and a¢ have the same action on the subspaces of the underlying spreads of π(C) and π(C ^t). From this it follows that U(∞) and U(0) of π(C ^t) are companions. Now the isomorphism f must map companions of π(C ^t) onto the companions of π(C). Therefore, we have either f: U(∞)→V(∞),U(0)→V(0), U(I)→V(P) or f: U(∞)→V(0), U(0)→V(∞), U(I)→V(Q), for some P,Q Î C.

If f maps U(∞), U(0) and U(I) onto V(0), V(∞), and V(Q), QÎ C, then df is an isomorphism from π(C ^t)  to π(C) mapping U(∞), U(0) and U(I) onto V(∞), V(0) and V(R) respectively for some R Î C. Without loss of generality, we may take that the isomorphism f maps U(∞), U(0) and U(I) onto V(∞), V(0) and V(X) respectively for some X Î C. By Proposition 2.3.3, the matrix representative set of π(C ^t) with fundamental subspaces U(∞), U(0) and U(I) is equivalent to the matrix representative set of π(C) with fundamental subspaces V(∞), V(0) and V(X) for some X Î C, i.e., C ^t is equivalent to C·X^-1. By (c) of Theorem 7.1, X Î C and V(X) is any one member taken from the orbits of S -{V(∞), V(0)} under H.

Hence the theorem.

REFERENCES