Journal of Surface Engineered Materials and Advanced Technology
Vol.06 No.02(2016), Article ID:65956,9 pages
10.4236/jsemat.2016.62008
Modeling the Adsorption Kinetics of Activated Carbon for Oil Vapor Recovery and Applications
Qi Wang1*, Zhipeng Wang2, Zhun Zhao3
1Bay Environmental Technology (Beijing) Corp., Beijing, China
2Department of Chemistry, Rice University, Houston, USA
3Chinese American Chemical Society, Houston, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2016; accepted 24 April 2016; published 27 April 2016
ABSTRACT
Oil Vapor recovery is a critical process in downstream chemical industries, in oil and gas industries and in environmental protection. For that purpose, highly-efficient absorbent materials for vapor recovery are in high demand and their associated adsorption kinetics is of great importance for their performance. As oil vapor consists of multiple components with different physical and chemical properties, modeling the overall adsorption kinetics of activated carbon for multi-com- ponent oil vapor is essentially valuable for industrial applications. In this work, we developed a comprehensive model of multi-component gas adsorption kinetics on activated carbon in a packed-bed reactor and numerically solved the model by the finite element method. The predictions from the model are all in the reasonable range indicating good validity of the model. Some dimensionless parameters are also derived to further investigate the prediction results.
Keywords:
Activated carbon, Oil Vapor Recovery, Adsorption, Multi-Component, Packed Bed

1. Introduction
In oil and gas industry, chemical industry and many other related industries, efficiently recovering the useful components from oil vapor is an essential part of their operations [1] - [5] . There are two major benefits for recovering oil vapor: 1) by recovering the valuable components from oil vapor, the company could make additional profits while reducing the cost, e.g. oil and gas companies are trying to recover natural gas vapor and to convert it to useful products; 2) oil vapor contains some environmental hazardous components which have to be recovered before they escape into the atmosphere. There are varieties of ways to recover oil vapor, including the method of creating negative pressure in the underground tank by withdrawal [6] , and the methods through physical adsorption mechanisms etc. [2] [3] [6] . Among all the different methods for oil vapor recovery, using efficient absorbents to physically capture the components of oil vapor at near atmospheric pressure is widely applicable in industry [1] [2] [5] [7] [8] .
Activated carbon is widely considered to be among the most effective industrial absorbents with extremely high surface-to-volume ratio, desired porous structures and excellent physical and chemical properties under different temperatures and pressures [9] - [13] . The oil vapor recovery system based on activated carbon absorbents has been extensively developed by many companies [1] - [3] [5] . The critical issue is to know its adsorption kinetics for oil vapor under certain range of temperature and pressure in order to understand the efficiency of the recovery system.
There are already some research works which theoretically investigate gas adsorption kinetics on a variety of absorbent materials [14] - [17] . Li. et al. [17] developed the comprehensive mathematical models for CO2 adsorption kinetics on sodium oxide promoted alumina in a packed-bed reactor. Their model fully explained the experimental results and uncovered some quantitative relationships between physical conditions and adsorption kinetics. There are also quite a few experimental works on exploring adsorption kinetics of activated carbon on organic vapor [1] - [3] . However, there are very few research works that develop adsorption kinetic models of activated carbon for multi-component systems. Since handling multi-component systems is in high demand in industry, developing mathematical models to predict adsorption kinetics of activated carbon for multi-component systems would be of critical importance in terms of understanding and optimizing the existing oil vapor recovery systems based on activated carbon.
In this paper, we developed a comprehensive mathematical model which describes the process of multi- component oil vapor adsorption on activated carbon in a packed-bed reactor. Our model predicts the adsorption kinetics under a wide range of dimensionless parameters and uncovers the quantitative relationships between kinetics and some dimensionless parameters. Although more comprehensive model could be further developed by taking into account of other processes, the results from this model serve as a good reference for designing more efficient oil vapor recovery systems based on activated carbon absorbents. We expect more experimental investigations to be done in order to validate our model.
2. Mathematical Models
Activated carbon is a highly-efficient adsorbent which is widely used in a variety of industries. There are already many existing research on studying physical properties of activated carbon which would affect its adsorption kinetics [18] - [22] . As oil vapor is a multi-component system and each of its component has different adsorption kinetic properties. Modeling the multi-component gas phase adsorption kinetics is of great importance as we can generalize our model to real industrial problems.
We start from the general model of BET equation, which studies the relationship between the equilibrium adsorption amount and the gas pressure. All the parameters we used are from the standard WS-470 activated carbon (Table 1), and we choose porosity to be 0.6.
Table 1. Parameters used in the simulation.
BET Equation
Let θ represent the loading fraction of oil vapors on activated carbon surface, N be the total number of sites on the surface of activated carbon, P represents the inlet gas pressure, 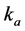 and
and 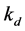 be rate constants for adsorption and desorption respectively, then we have:
be rate constants for adsorption and desorption respectively, then we have:
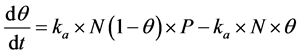
We solve this kinetic equation and get:
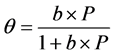
where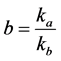 .
.
According to the Arrhenius Equation, we have:
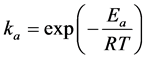
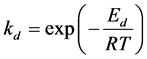
where Ea and Eb represent the activation energies for adsorption and desorption processes, respectively.
So

which decreases with increasing temperature.
The plot shown below (Figure 1) illustrates the quantitative relationship between loading fraction 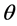 and gas pressure P/P0 at 298, 400 and 500 K.
and gas pressure P/P0 at 298, 400 and 500 K.
BET equation is a good way to model gas adsorption kinetics on activated carbon, but it is only applicable for one-component gas adsorption. In the following part the comprehensive model is presented for the multi-com- ponent oil vapor recovery.
Figure 1. Simulated BET curve at different temperatures of activated carbon.
3. Multi-component Oil Vapor Adsorption in Packed-Bed Reactor
Mathematical Model
From convection-diffusion model, we have the following:
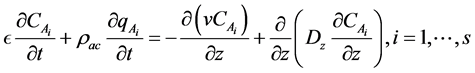
We assume that the oil vapor gases follow the ideal gas law, we have:
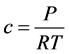
where C is the total molar (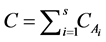 ).
).
P is the pressure and T is the temperature. We also assume that adsorption follows the linear driving force model [23] . Based on this model, we have:
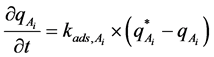 .
.
We further assume the superficial velocity is constant through- out the whole packed-bed reactor. Under the low concentration of oil vapor gas, we make all the quantities dimensionless in the following partial differential equations (PDEs), which is for a single component adsorption model:

With the Boundary Condition as follow:
The characteristic time of the reactor is defined as:
which is the Peclet number, and the Damkohler number for adsorption



With the Boundary Condition as follows:
The above dimensionless PDEs can be solved numerically using finite element methods. Typiclaly the adsorption kinetics is very fast such that equilibrium is reached very quickly, such that 

An analytical solution can be obtained for
where erfc is the complementary error function.
This is a very good way to approximate the dimensionless quantity
4. Results and Discussion
We already presented a comprehensive model which quantitatively predicts the adsorption kinetics for oil vapor recovery in a packed-bed reactor. In this model we only consider the diffusion in axial direction, and use mass conservation equation to simulate the spatial-temporal profiles of oil-vapor adsorption. We assume that activated carbon adsorption is operated in constant temperature, and the oil vapor concentration is very low compared with adsorption capacity of activated carbon. Table 1 illustrates the parameters we used in the simulation.
Furthermore, no chemical reactions occur between components in oil vapor is assumed, so each component can be treated as an independent adsorbate. So the multi-component adsorption problem could be converted to the single component adsorption problem. The plot below (Figure 2) illustrates the temperature dependence of the adsorption kinetics.
Figure 2. Effect of temperatures on breakthrough curve of oil vapor on packed-bed reactor of activated carbon (the temporal dynamics of adsorbate concentration at the exit of reactor, porosity = 0.6).
From Figure 2 We can see that higher temperature would decrease the adsorption capacity of activated carbon due to the fact that adsorption process is exothermic while increase the adsorption kinetics resulting in faster breakthrough, meaning the adsorbate (oil vapor) would reside shorter time in activated carbon reactor under higher temperatures compared with lower temperatures.
The adsorption kinetics at three different porosities of activated carbon is simulated at temperature of 298 K (Figure 2). The C/C0 is calculated via multi-components weighted average (we simulate the adsorption kinetics for each component, calculating their corresponding breakthrough curve, and derive the weighted average in terms of their volume fraction in the original oil vapor). It can be seen in Figure 3 that higher porosity could result in longer breakthrough time, consistent with the fact that higher porosity would result in higher surface areas and would make longer residence time for adsorbate in the reactor.
The comprehensive study across all the parameter space in terms of porosity and temperature is shown in Figure 4. We can see that higher porosity and lower temperature would result in longer residence time for the adsorbate in the reactor. Higher temperature would result in faster adsorption rate but would lower the adsorption capacity for activated carbon adsorbent.
Figure 3. Breakthrough curves of oil vapor for different porosities of activated carbon (temporal dynamics of concentrations at the exit of packed-bed reactor).
Figure 4. Effects of porosity and temperature on breakthrough time of oil vapor adsorption in activated carbon.
In Figure 5, we show the spatial-temporal profile of Pentane adsorption loadings on activated carbon. Pentane is one of the major components in oil vapor. Since we assumed that the activated carbon is under the constant temperature during the adsorption process, and the concentration of oil vapor is very low, the linear driving force model could perfectly model the adsorption kinetics of adsorbate. Other components in oil vapor could be simulated in the same way.
In Figure 6, we simulated the spatial-temporal profile of concentration of Pentane in the packed-bed reactor. With the assumption of low concentration and constant temperature (T = 298 K), we can numerically solve the dimensionless PDEs with finite element method. We assume the initial condition that C/C0(0, t) = 1 and C/C0(0, 0) = 1 while C/C0(z,0) = 0.
Figure 7 below shows the adsorption kinetics for three different components: Pentane, Hexane and Butane. Hexane has the highest “breakthrough” concentration, while n-Butane has the lowest “breakthrough” concentration. This is because the adsorption mass transfer rate is inversely correlated with the molecular weights. Hexane has larger molecular weight which results in smaller amount of molecules being adsorbed onto the surface of activated carbon. As we assume linear driving force model for adsorption, higher mass transfer rate would result in more effective adsorption and faster adsorption kinetics (Figure 7).
Figure 5. Spatial-Temporal profile of loadings of Pentane on activated carbon adsorbent in the packed-bed reactor.
Figure 6. Spatial-Temporal Profile of Pentane concentration in the packed-bed reactor of activated carbon.
Figure 7. Simulated breakthrough curve for three major components (Pentane, Hexane, and Butane) of oil vapor in the packed-bed reactor of activated carbon.
5. Conclusion
In this study, the adsorption kinetics of oil vapor on activated carbon was simulated through convection-diffu- sion model. From simulation results, we can conclude that both porosity and temperature have significant effects on adsorption kinetics of oil vapor. Higher porosity would increase the adsorption kinetics of activated carbon, while higher temperature would decrease the adsorption capacity of activated carbon, although it could increase the kinetics of adsorption and could accelerate the adsorption process to reach equilibrium. Also different components in oil vapor show drastically different adsorption kinetic properties. This is due to the fact that different components have different effective mass transfer rate, as they differ in molecular weights as well as chemical and physical properties. This study serves as an important theoretical basis for future experimental research on large-scale oil vapor recovery with activated carbon.
Acknowledgements
This work is partly supported by International Science and Technology Cooperation Program of China (ISTCP) (Grant No. 2014DFA90420) and Bay Environmental Technology Corp at Beijing, China.
Cite this paper
Qi Wang,Zhipeng Wang,Zhun Zhao, (2016) Modeling the Adsorption Kinetics of Activated Carbon for Oil Vapor Recovery and Applications. Journal of Surface Engineered Materials and Advanced Technology,06,80-88. doi: 10.4236/jsemat.2016.62008
References
- 1. Cheripally, G.S., Mannava, A., Kumar, G., Gupta, R., Saha, P., Mandal, B., Uppaluri, R., Gumma, S. and Ghoshal, A.K. (2012) Measurement and Modeling of Adsorption of Lower Hydrocarbons on Activated Carbon. Journal of Chemical & Engineering Data, 58, 1606-1612.
http://dx.doi.org/10.1021/je3013217 - 2. Malek, A. and Farooq, S. (1997) Kinetics of Hydrocarbon Adsorption on Activated Carbon and Silica Gel. AIChE Journal, 43, 761-776.
http://dx.doi.org/10.1002/aic.690430321 - 3. Prakash, J., Nirmalakhandan, N. and Speece, R.E. (1994) Prediction of Activated Carbon Adsorption Isotherms for Organic Vapors. Environmental Science & Technology, 28, 1403-1409.
http://dx.doi.org/10.1021/es00057a005 - 4. Rufford, T.E., Watson, G.C.Y., Saleman, T.L., Hofman, P.S., Jensen, N.K. and May, E.F. (2013) Adsorption Equilibria and Kinetics of Methane + Nitrogen Mixtures on the Activated Carbon Norit RB3. Industrial & Engineering Chemistry Research, 52, 14270-14281.
http://dx.doi.org/10.1021/ie401831u - 5. Wu, J.W., Madani, S.H., Biggs, M.J., Phililp, P., Chen, L. and Hu, E.J. (2015) Characterizations of Activated Carbon-Methanol Adsorption Pair Including the Heat of Adsorptions. Journal of Chemical & Engineering Data, 60, 1727-1731.
http://dx.doi.org/10.1021/je501113y - 6. HY-BON/EDI.
http://hy-bon.com/products/vru/ - 7. Yang, C., Kaipa, U., Mather, Q.Z., Wang, X.P., Nesterov, V., Venero, A.F. and Omary, M.A. (2011) Fluorous Metal-Organic Frameworks with Superior Adsorption and Hydrophobic Properties toward Oil Spill Cleanup and Hydrocarbon Storage. Journal of the American Chemical Society, 133, 18094-18097.
http://dx.doi.org/10.1021/ja208408n - 8. Wang, X.-S., Liu, J., Bonefont, J.M., Yuan, D.-Q., Thailapally, P.K. and Ma, S.O. (2013) A Porous Covalent Porphyrin Framework with Exceptional Uptake Capacity of Saturated Hydrocarbons for Oil Spill Cleanup. Chemical Communications, 49, 1533-1535.
http://dx.doi.org/10.1039/c2cc38067f - 9. Sircar, S., Golden, T.C. and Rao, M.B. (1996) Activated Carbon for Gas Separation and Storage. Carbon, 34, 1-12.
http://dx.doi.org/10.1016/0008-6223(95)00128-X - 10. Corapcioglu, M.O. and Huang, C.P. (1987) The Adsorption of Heavy Metals onto Hydrous Activated Carbon. Water Research, 21, 1031-1044.
http://dx.doi.org/10.1016/0043-1354(87)90024-8 - 11. Matranga, K.R., Myers, A.L. and Glandt, E.D. (1992) Storage of Natural Gas by Adsorption on Activated Carbon. Chemical Engineering Science, 47, 1569-1579.
http://dx.doi.org/10.1016/0009-2509(92)85005-V - 12. Siriwardane, R.V., Shen, M.-S., Fisher, E.P. and Poston, J.A. (2001) Adsorption of CO2 on Molecular Sieves and Activated Carbon. Energy & Fuels, 15, 279-284.
http://dx.doi.org/10.1021/ef000241s - 13. Dabrowski, A., Podkoscielny, P., Hubicki, Z. and Barczak, M. (2005) Adsorption of Phenolic Compounds by Activated Carbon—A Critical Review. Chemosphere, 58, 1049-1070.
http://dx.doi.org/10.1016/j.chemosphere.2004.09.067 - 14. Yang, R.T. and Doong, S.J. (1985) Gas Separation by Pressure Swing Adsorption: A Pore-Diffusion Model for Bulk Separation. AIChE Journal, 31, 1829-1842.
http://dx.doi.org/10.1002/aic.690311109 - 15. Kapoor, A., Ritter, J.A. and Yang, R.T. (1990) An Extended Langmuir Model for Adsorption of Gas Mixtures on Heterogeneous Surfaces. Langmuir, 6, 660-664.
http://dx.doi.org/10.1021/la00093a022 - 16. Li, J.-R., Kuppler, R.J. and Zhou, H.-C. (2009) Selective Gas Adsorption and Separation in Metal-Organic Frameworks. Chemical Society Reviews, 38, 1477-1504.
http://dx.doi.org/10.1039/b802426j - 17. Li, M. (2011) Dynamics of CO2 Adsorption on Sodium Oxide Promoted Alumina in a Packed-Bed Reactor. Chemical Engineering Science, 66, 5938-5944.
http://dx.doi.org/10.1016/j.ces.2011.08.013 - 18. Molina-Sabio, M., RodRiguez-Reinoso, F., Caturla, F. and Sellés, M.J. (1995) Porosity in Granular Carbons Activated with Phosphoric Acid. Carbon, 33, 1105-1113.
http://dx.doi.org/10.1016/0008-6223(95)00059-M - 19. Py, X., Guillot, A. and Cagnon, B. (2003) Activated Carbon Porosity Tailoring by Cyclic Sorption/Decomposition of Molecular Oxygen. Carbon, 41, 1533-1543.
http://dx.doi.org/10.1016/S0008-6223(03)00092-7 - 20. Chiang, Y.-C., Chiang, P.-C. and Huang, C.-P. (2001) Effects of Pore Structure and Temperature on VOC Adsorption on Activated Carbon. Carbon, 39, 523-534.
http://dx.doi.org/10.1016/S0008-6223(00)00161-5 - 21. Marzal, P., Seco, A., Gabaldon, C. and Ferrer, J. (1999) Cadmium and Zinc Adsorption onto Activated Carbon: Influence of Temperature, pH and Metal/Carbon Ratio. Chemical Technology and Biotechnology, 66, 279-285.
http://dx.doi.org/10.1002/(SICI)1097-4660(199607)66:3<279::AID-JCTB506>3.0.CO;2-K - 22. Lozano-Castello, D., Cazorla-Amoros, D., Linares-Solano, A. and Quinn, D.F. (2002) Influence of Pore Size Distribution on Methane Storage at Relatively Low Pressure: Preparation of Activated Carbon with Optimum Pore Size. Carbon, 40, 989-1002.
http://dx.doi.org/10.1016/S0008-6223(01)00235-4 - 23. Sircar, S. and Hufton, J.R. (2000) Why Does the Linear Driving Force Model for Adsorption Kinetics Work? Adsorption, 6, 137-147.
http://dx.doi.org/10.1023/A:1008965317983
NOTES
*Corresponding author.

















