Geomaterials
Vol.3 No.4(2013), Article ID:38561,7 pages DOI:10.4236/gm.2013.34021
Resilient Modulus of Compacted Lateritic Soils from Senegal at OPM Conditions
1Laboratoire de Mécanique et Modélisation—UFR Sciences de l’ Ingénieur, Université de Thiès, Thiès, Sénégal
2Laboratoire d’ Alembert—Université Pierre et Marie Curie, Paris, France
Email: fatou.samb@univ-thies.sn
Copyright © 2013 Fatou Samb et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 3, 2013; revised October 3, 2013; accepted October 10, 2013
Keywords: Gravel Lateritic Soils; Resilient Modulus; Mechanical Behaviour; Pavement; Cyclic Triaxial Test; Mechanistic Design
ABSTRACT
Repeated load triaxial tests were performed on five compacted gravel lateritic soils collected from different locations in Senegal: Sébikotane, Dougar, Pâ Lo, Mont-Rolland and Ngoundiane. The study revealed that resilient modulus decreases with the increase of the bulk and deviatoric stress in constant confining pressure. In addition, resilient modulus increases with the percentage of cement for appreciably equal contents of moisture. This effect tends to stop for higher stress. Besides, correlations were made with some models of resilient modulus such as the Uzan-Witczack model (Witczack and Uzan, 1988 [1]) and the National Highway Research Program (NCHRP) model (2004 [2]). The study confirms that both models give very good results with the best correlations being obtained with the Uzan-Witczack model.
1. Introduction
Since several decades, gravel lateritic soils have been used in road pavements in tropical countries. In Senegal, the increased use of this material has lead to a rarefaction of careers of good quality. Therefore, the rationalization of existing resources requires a real knowledge of lateritic soils. This problem has drawn the attention of the researchers who have done a lot to understand the mechanical behaviour of lateritic gravels (Samb, 1986 [3]; Fall, 1993 [4]; Fall, Sawangsuriya, Benson, Edil and Bosscher, 2007 [5]).
Under cyclic loading, road materials are characterized by a fast increase of permanent strains from the first cycles of loading. As the number of cycles increases, these deformations stabilize and the behaviour becomes essentially reversible allowing to define a module called “resilient modulus” (Yoder and Witzack, 1975 [6]; Paute, Hornych and Benaben, 1994 [7]; Martinez, 1990 [8]). Resilient modulus represents the unloading modulus after several repeated cycles of loading, allowing to simulate road traffic (Figure 1):
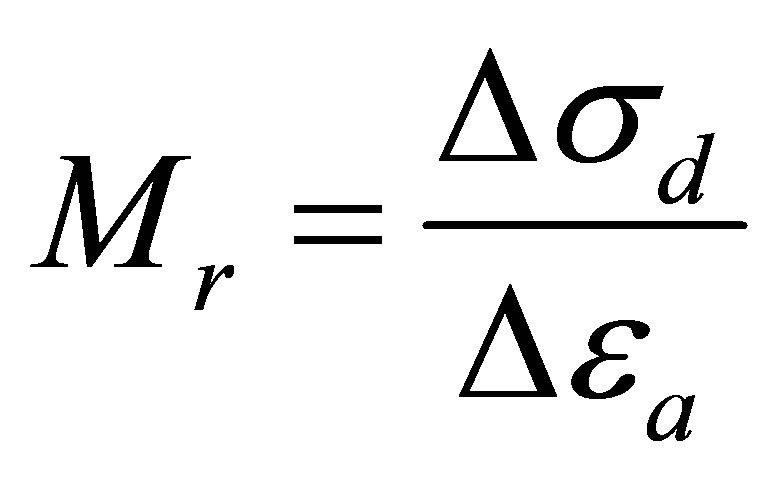 (1)
(1)
Δσd = σ1 − σ3 = Deviatoric stress; σ1 = Major principal stress; σ3 = Minor principal stress et Δεa = Resilient axial strain.
In order to study the cyclic behaviour of gravel lateritic soils of Senegal, repeated load triaxial tests were conducted on soils collected from Sébikotane, Dougar. Ngoundiane, Pâ Lo and Mont-Rolland.
In this paper, we aim to present the experimental protocol, the determination of average resilient modulus as well as the evolution of the resilient modulus according to the level of stress and the percentage of cement. Furthermore, correlations are made depending on some gen-
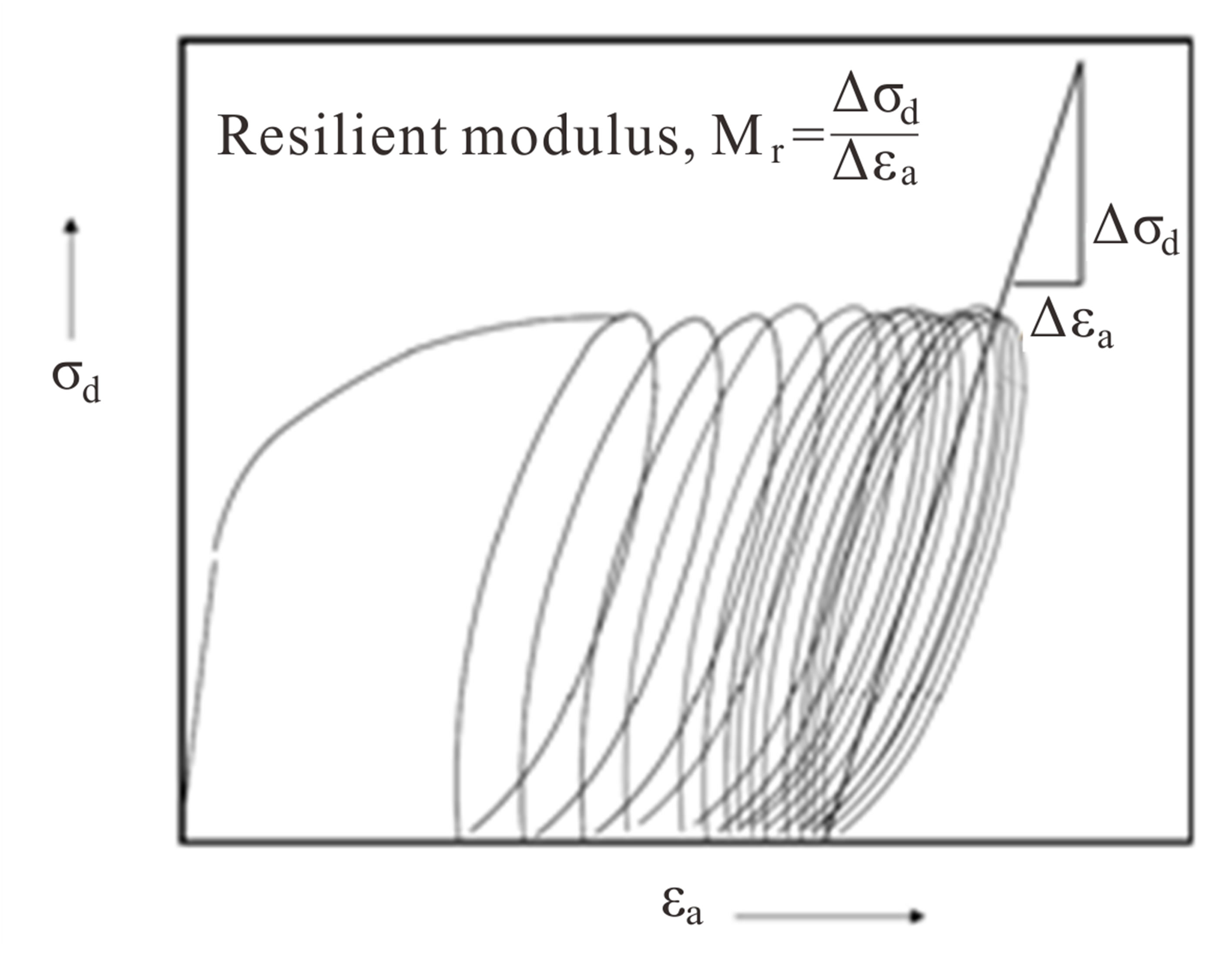
Figure 1. Definition of resilient modulus (Hopkins, Beckham and Sun, 2007 [9]).
eralized resilient modulus models such as Uzan-Witczack (Witczack and Uzan, 1988 [1]) and the NCHRP model (2004 [2]).
2. Material and Methods
Standard laboratory road tests were performed to classify the materials and to determine their properties. Laboratory tests consisted of particle size analysis, consistency limits. Modified Proctor Compaction test and Californian Bearing Ratio test.
The cyclic triaxial tests were then conducted to determine the resilient modulus of these soils. For this purpose, unbound gravel lateritic soils and that improved with cement (1%, 2% and 3%) were compacted in 95% of Modified Optimum Proctor (OPM) that corresponds to the value retained in road specifications of base layers. Samples are 70 mm in diameter and 180 mm height.
The Tables 1 and 2 respectively present the summary of results of the identification test sand the nomenclature of test specimens for triaxial tests.
The experimental procedure is described by the NCHRP (2004 [2]). The triaxial apparatus in repeated loads is the experimental reference device used to characterize the mechanical behaviour of roads materials (Figure 2).
The study of resilient behaviour includes two phases. In the first one, the test begins with a conditioning which consists in applying a minimum of 1000 repetitions of a load equivalent to a cyclic stress of 207 kPa using a haversine-shaped 0.1-second load pulse followed by a 0.9- second rest period.
During the second phase, the test specimen is submitted to cyclic loading by applying a number of 100 repetitions of the corresponding cyclic axial stress using the same load pulse according to various loading paths given in Table 3.
The axial deformations are measured by two external and two internal displacements sensors called “Linear Variable Differential Transformers” (LVDT). The average deformations for each LVDT separately for the last five cycles are reported then the resilient modulus is calculated (NCHRP, 2004 [2]).
It is important to notice that the results of the resilient modulus exposed below are the ones obtained with the external deformation sensors.
3. Results and Discussion
3.1. Comparision between Static and Cyclic Modulus
Table 4 gives the values of average resilient modulus for all the materials as well as the maximal modulus found for the Unconfined Compression Test (UCT) realized on the same types of test tubes for the sites of Mont-Rolland. Dougar and Pâ Lo. In general, it is observed that resilient modulus is much more important for cyclic triaxial test than for the unconfined compression test. Indeed, the application of an increasing monotonous load is more unfavorable than the application of a cyclic load where the sample gets back part of the deformation. Furthermore, the conditioning made in the cyclic test allows increasing the stiffness of the material; which is not the case for the compression test.
On the other hand, the ratio between resilient modulus and Young modulus for the compression test seems much more high for the raw material (between 12% and 17%) and decreases with the percentage of cement. Indeed. The increase of the stiffness of the material with the percentage of cement decreases the sample deformability.
These results are very important because they show the reason why it is necessary to take into account the real stiffness of the gravel lateritic soils in mechanistic design. The use of the static modulus does not seem to be
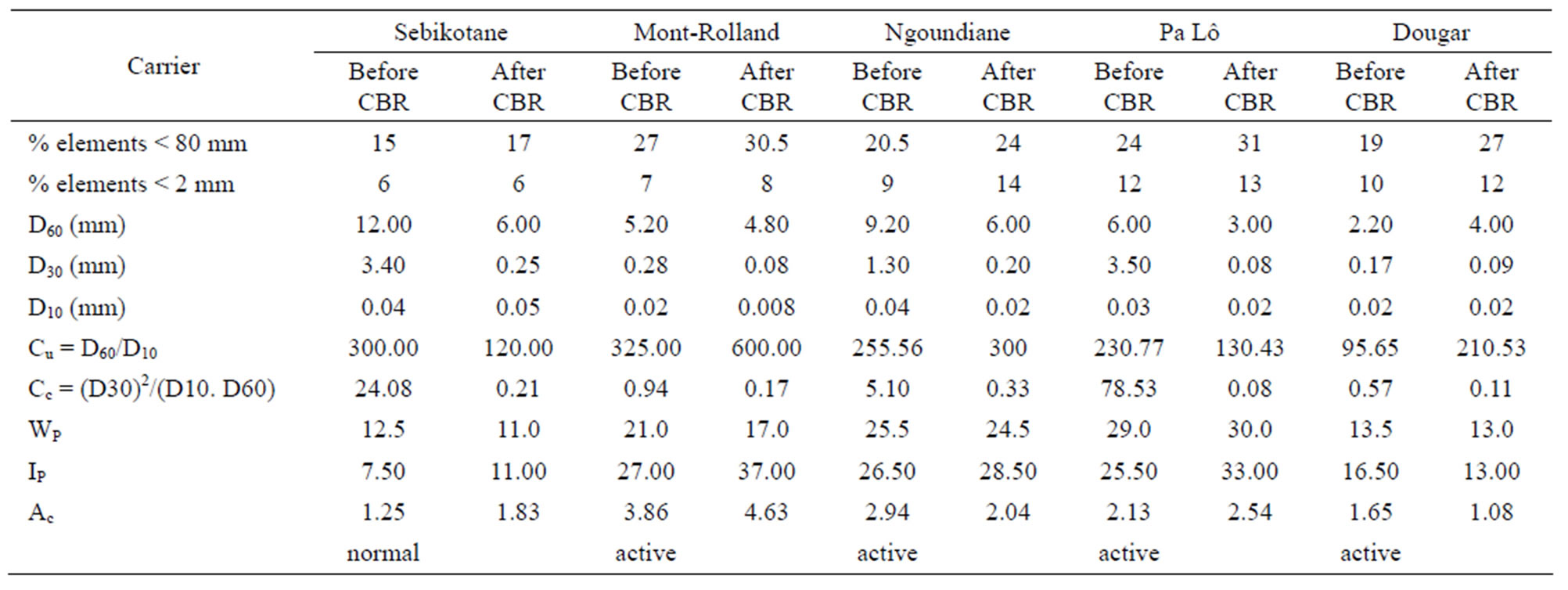
Table 1. Identification test results of collected gravel lateritic soils.
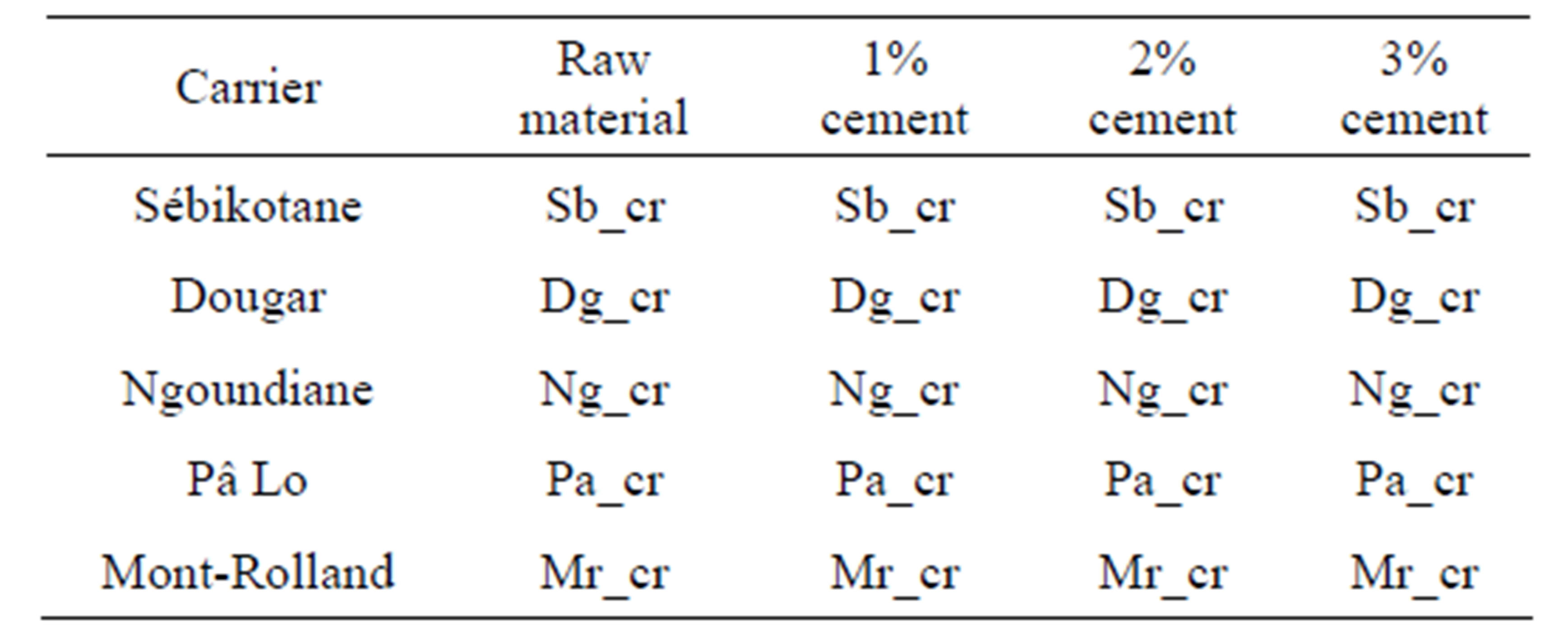

Table 2. Nomenclature of test specimens for load triaxial tests and unconfined compression tests.
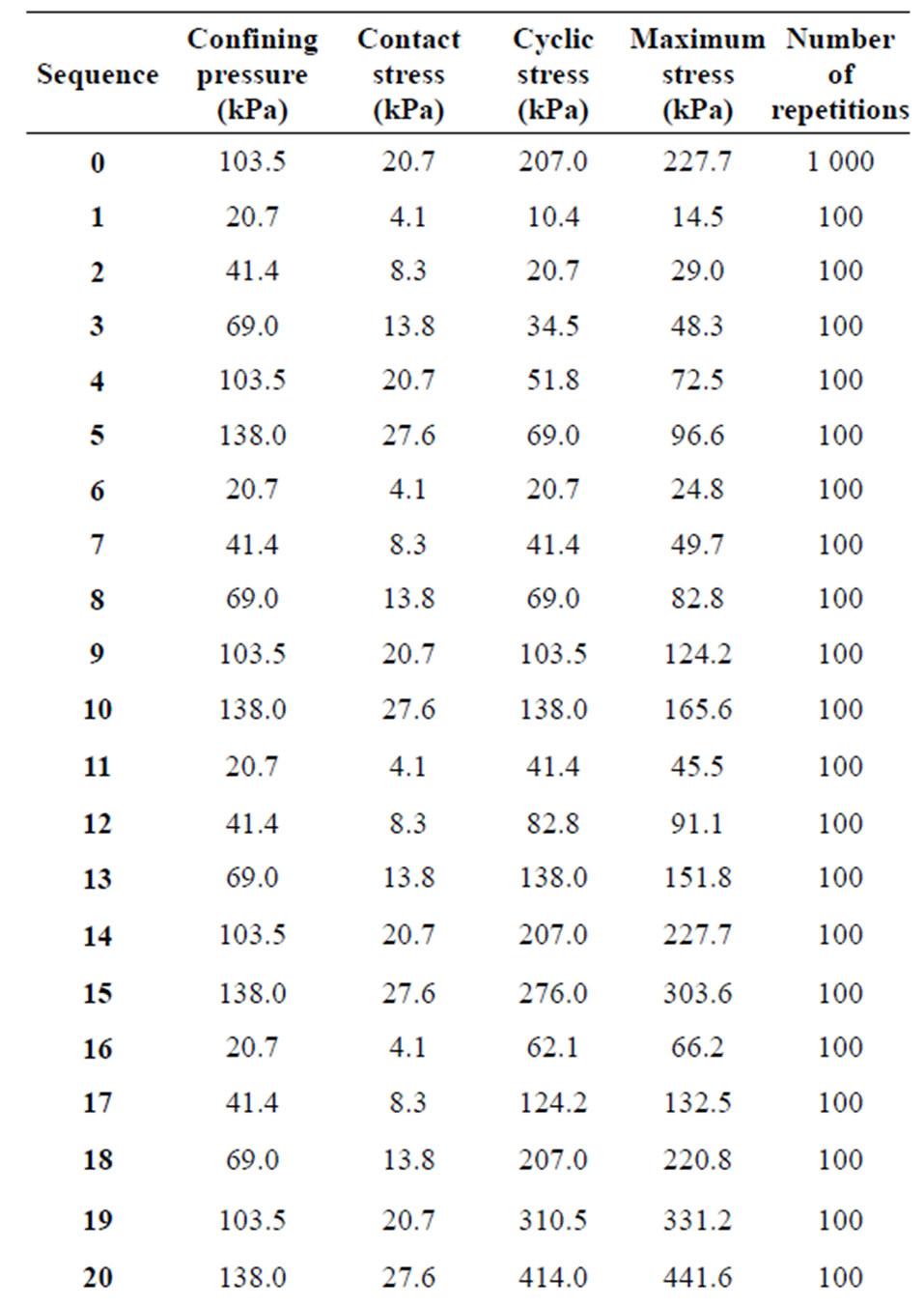
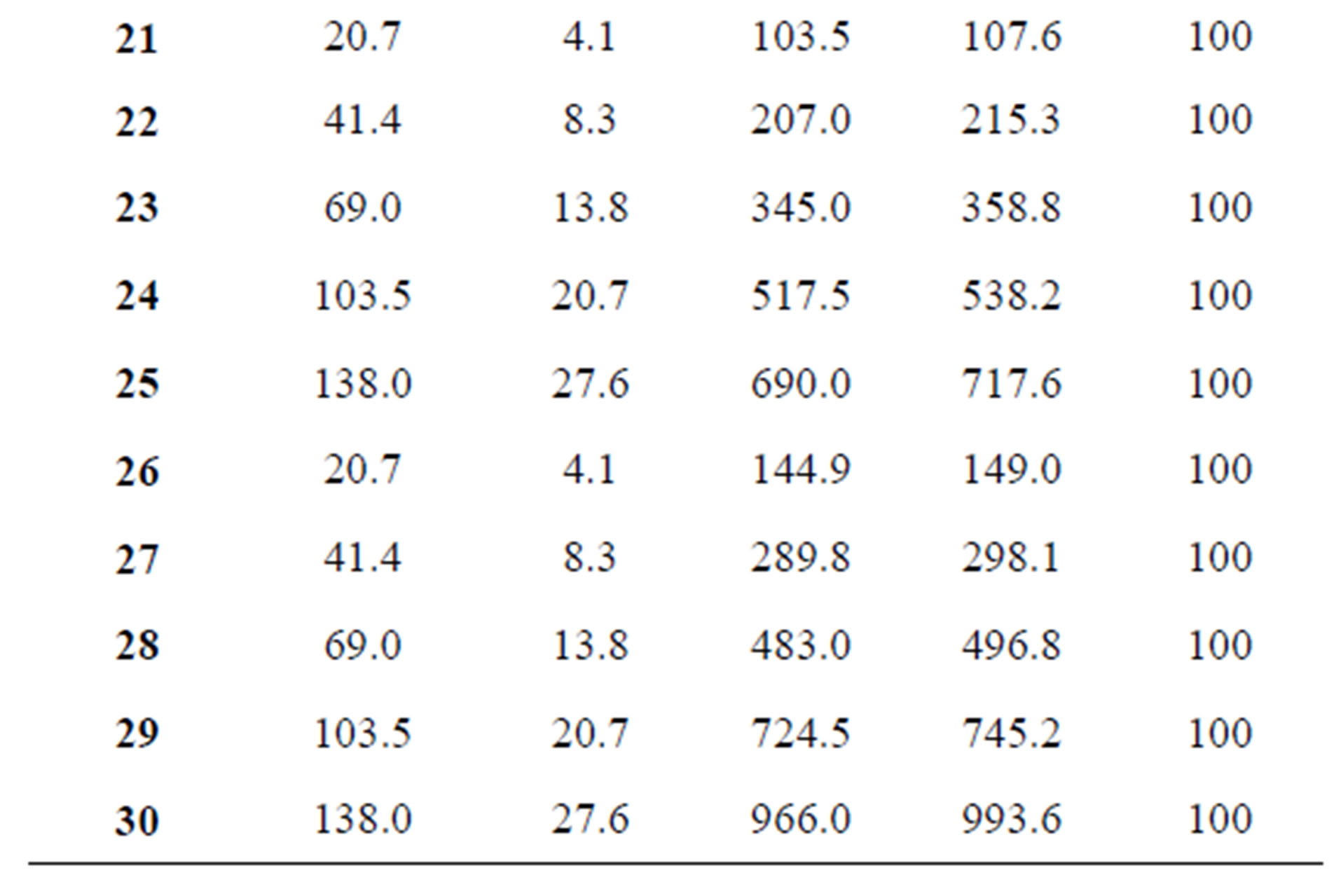
Table 3. Test sequence for base or subbase materials— Procedure Ia of NCHRP (2004) [2].
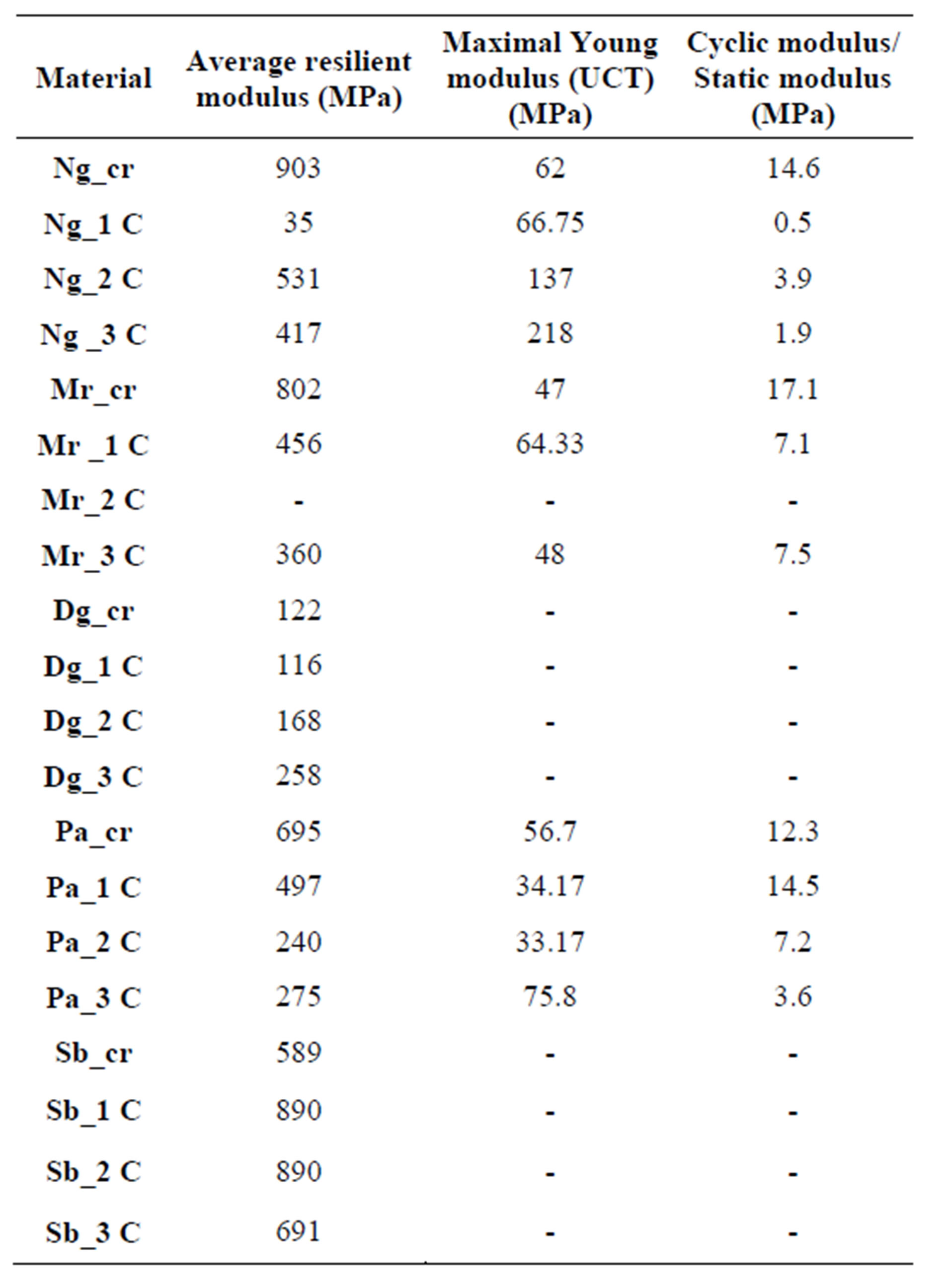
Table 4. Comparision between static and cyclic modulus.

Figure 2. Triaxial apparatus for cyclic loading—University of Madison (Bâ, 2012 [10]).
any more suitable for pavement design.
3.2. Resilient Modulus According to the Level of Stress
Previous investigations, from the earlier studies reported by Williams (1963) [11] to the recent studies by Kolisoja (1997) [12], have shown that generally stress level is the factor that has the most significant impact on resilient properties of road materials (Lekarp, Isacsson and Dawson, 2000 [13]). In this part, the effect of the bulk and deviatoric stress as well as the percentage of cement are analyzed.
3.2.1. Effect of Bulk Stress
The Figures 3 and 4 show that resilient modulus decreases inversely with the increase of bulk stress in constant confining pressure. Indeed, gravel lateritic soils have a low void ratio after compaction because of the presence of fine grains which ensures the cohesion. After application of the load and a generation of fine particles (because of the disintegration of pisolithes), new surfaces of discontinuities are created, involving an increase of the void ratio and therefore a loss of resistance.
3.2.2. Effect of Deviatoric Stress
The Figures 5 and 6 show that resilient modulus decreases according to deviatoric stress in constant confining pressure. These results confirm the fact, the increase of the level of stress in the material generally leads to a decrease of the rigidity of gravel lateritic soils samples.
3.2.3. Effect of the Percentage of Cement
The effect of the percentage of cement was studied for gravel lateritic soils of Dougar, Sebikotane and Pâ Lo (Figures 7-9). The observations showed an increase of resilient modulus according to the percentage of cement for the materials of Dougar. However, this result is not confirmed for gravel lateritic soils of Sebikotane and Pâ Lo.
Besides, the observation of the moisture contents measured as in Table 5 showed that resilient modulus decreases with the important increase of the moisture
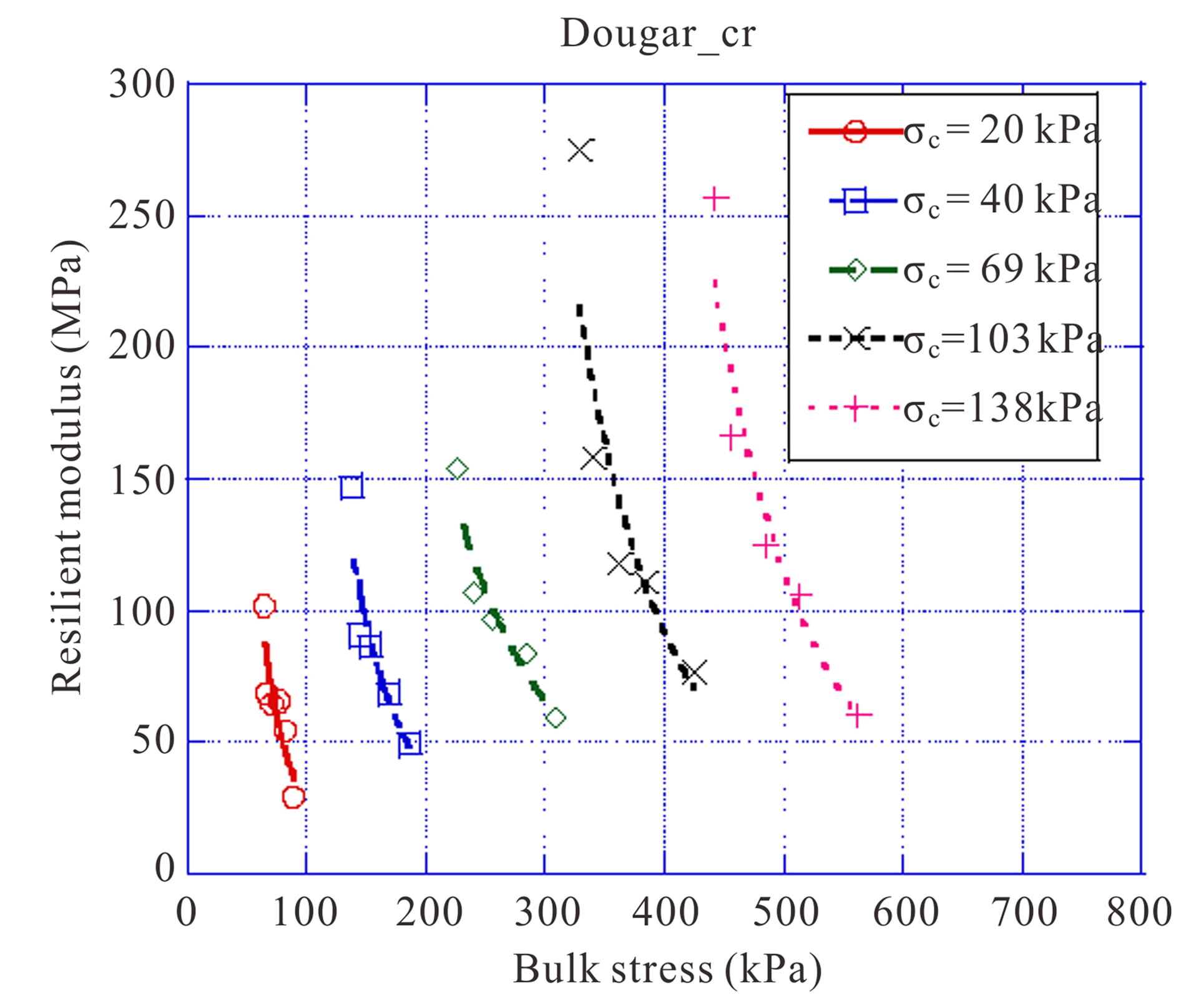
Figure 3. Variation of resilient modulus with bulk stress— Unbound gravel lateritic soil of Dougar.

Figure 4. Variation of resilient modulus with bulk stress— Dougar 1% cement.
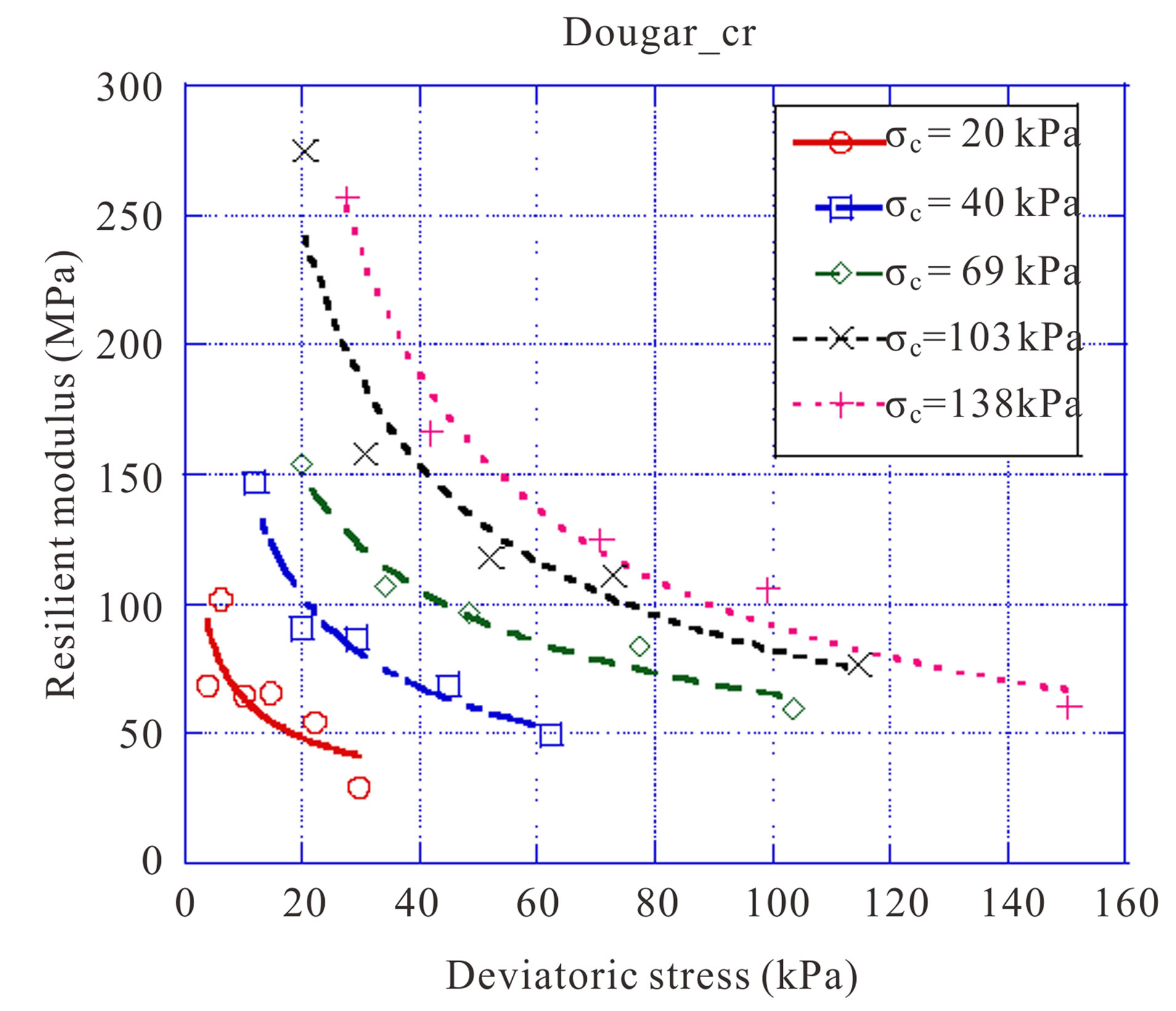
Figure 5. Variation of resilient modulus with deviatoric stress—Unbound gravel lateritic soil of Dougar.
content (Sebikotane 3%. Pâ Lo 3%). Furthermore, for materials from Dougar, the resilient modulus increases with the percentage of cement, for appreciably equal moisture contents. The resilient modulus seems to be affected more by moisture content effect than that of the percentage of cement.
4. Review of Resilient Modulus Models
Prediction of roads behaviour requires stress-strain relationships modelling by constitutive laws. Several models were proposed in the literature. The K-θ model (Seed, Mitry, Monismith and Chan, 1967 [14]; Brown and Pell, 1967 [15]; Hicks and Monismith, 1971 [16]) which is one of the most popular models expresses the resilient modulus according to the bulk stress:

Figure 6. Variation of resilient modulus with deviatoric stress—Dougar 1% cement.
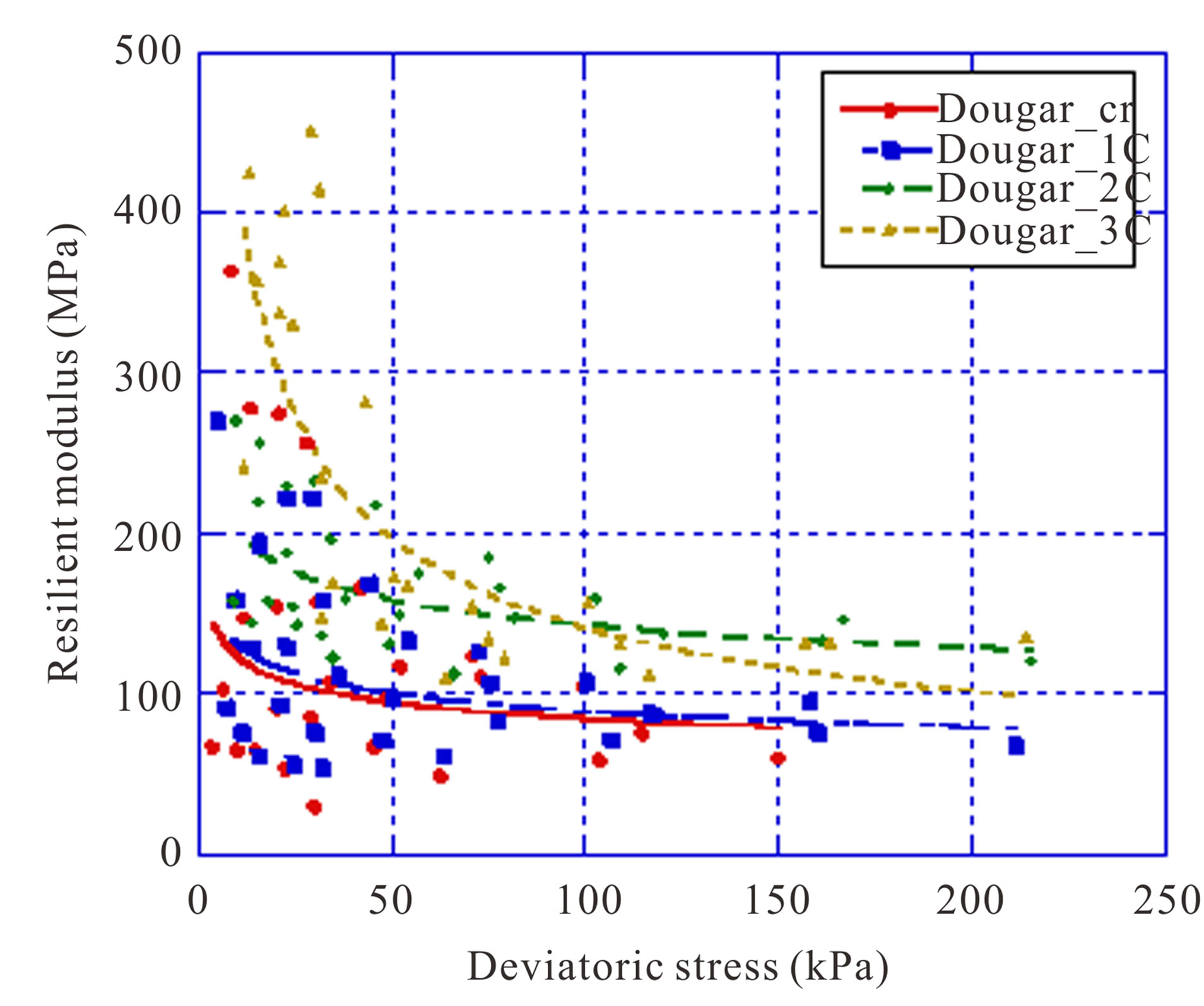
Figure 7. Effect of the percentage of cement on resilient modulus of gravels lateritics soils of Dougar.
 (2)
(2)
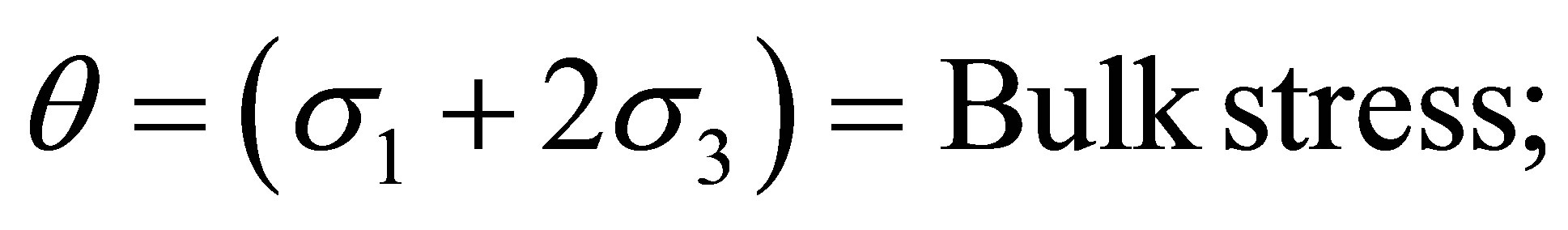 k1 and k2 are the regression constants.
k1 and k2 are the regression constants.
It is widely used to model the resilient modulus as a function of the level of stress applicable to the granular materials. However, the K-θ model presents some disavantages. Uzan (1985 [17]) introduces the deviatoric stress as the additional component according to the effect of shearing behaviour and obtains better correlations with the trial results:
 (3)
(3)
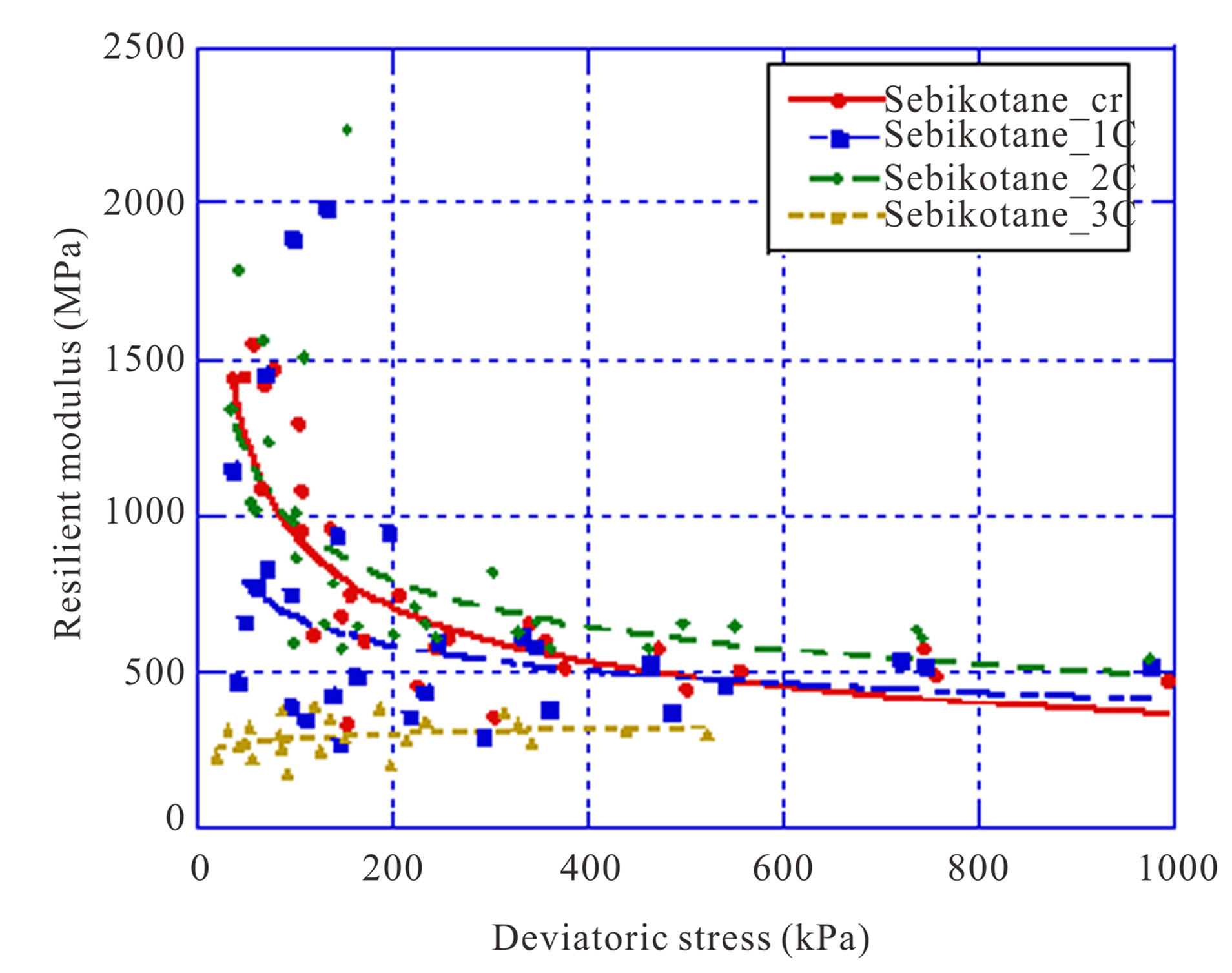
Figure 8. Effect of the percentage of cement on resilient modulus of gravels lateritics soils of Sebikotane.
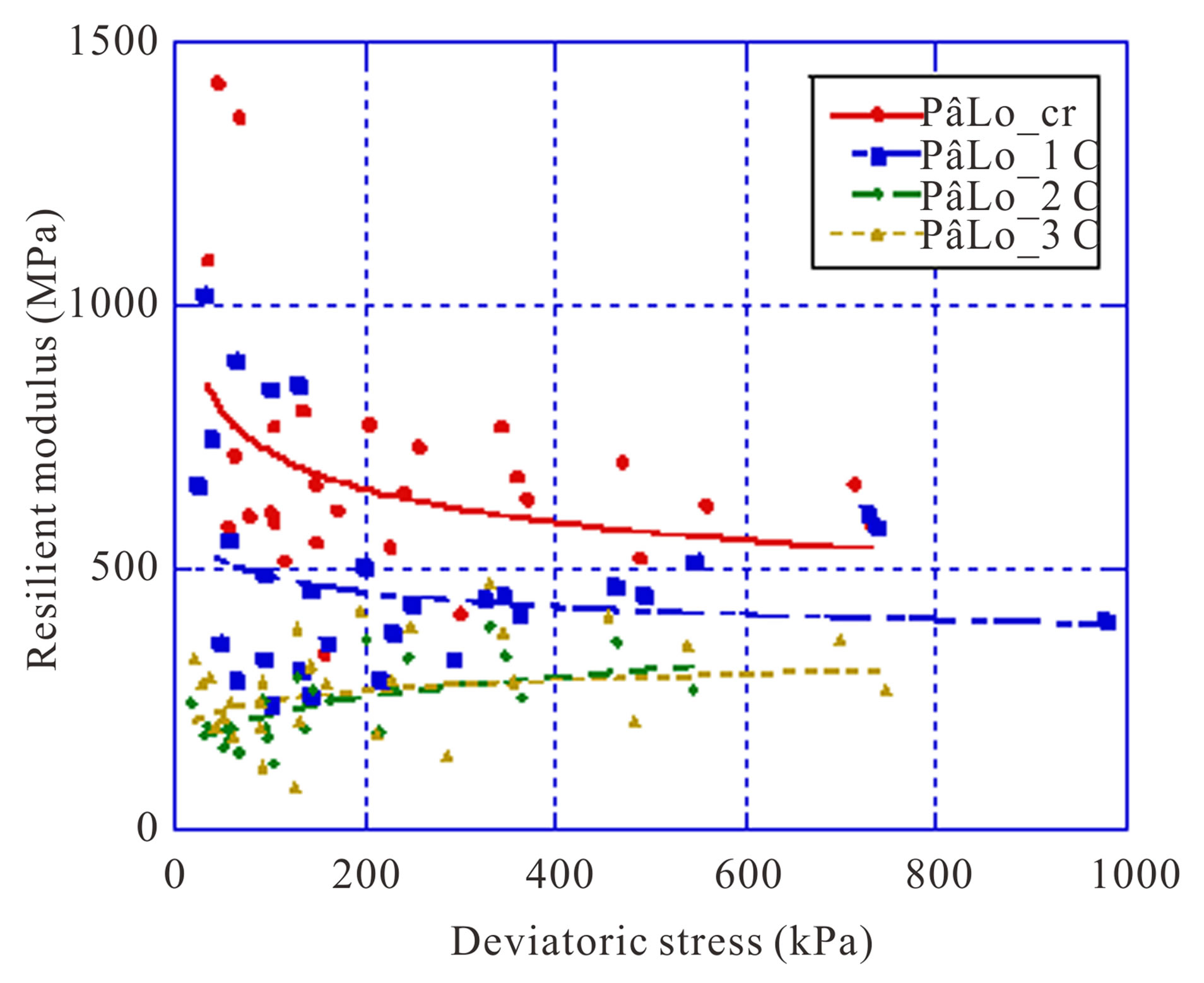
Figure 9. Effect of the percentage of cement on resilient modulus of gravels lateritics soils of Pâ Lo.
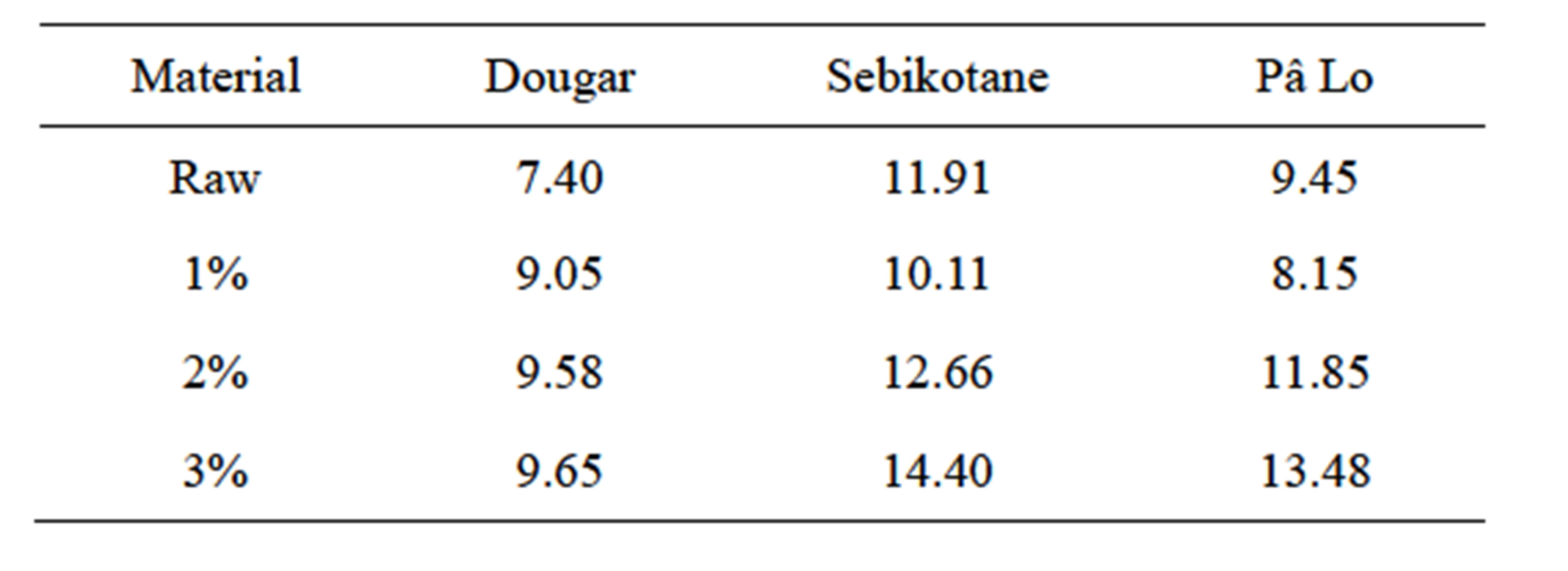
Table 5. Water content of soils samples after tests.
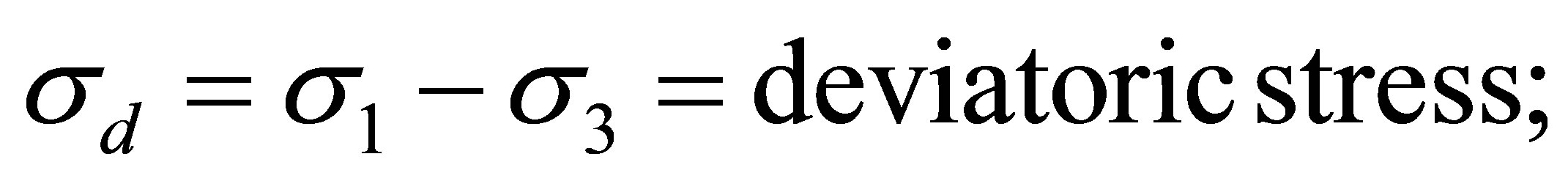 k1, k2 and k3 regression constants.
k1, k2 and k3 regression constants.
Witczack and Uzan (1988 [1]) proposes an improvement of the model of Uzan (1985 [17]) the by replacing the octahedral shear stress:
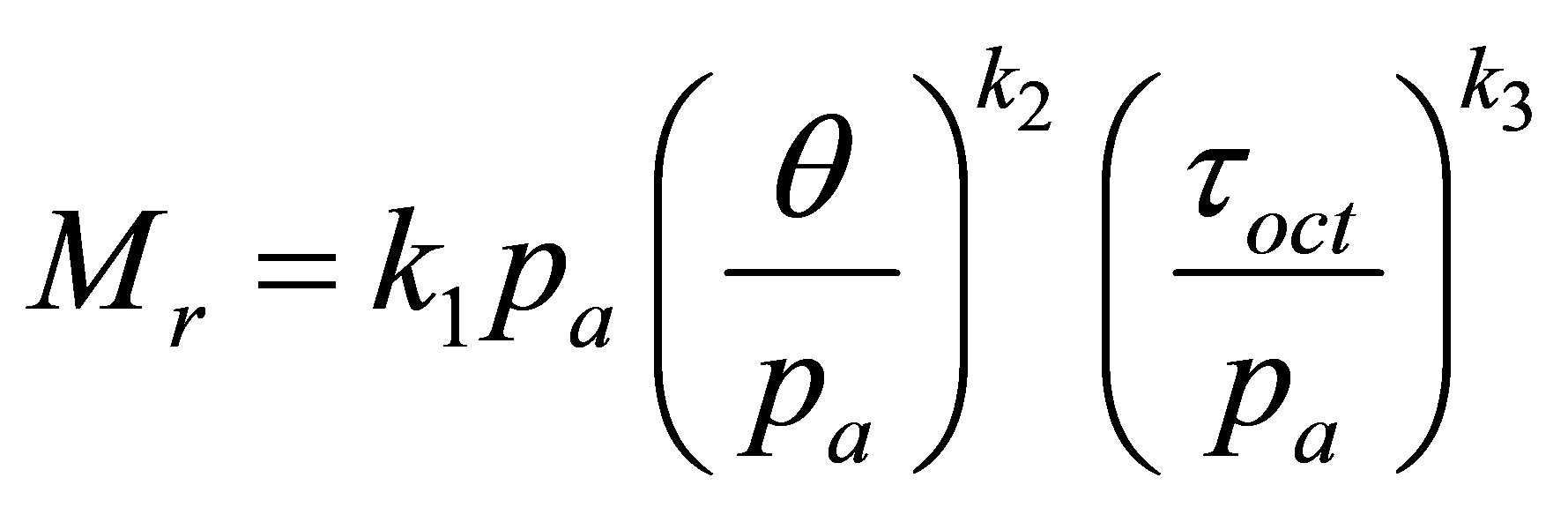 (4)
(4)
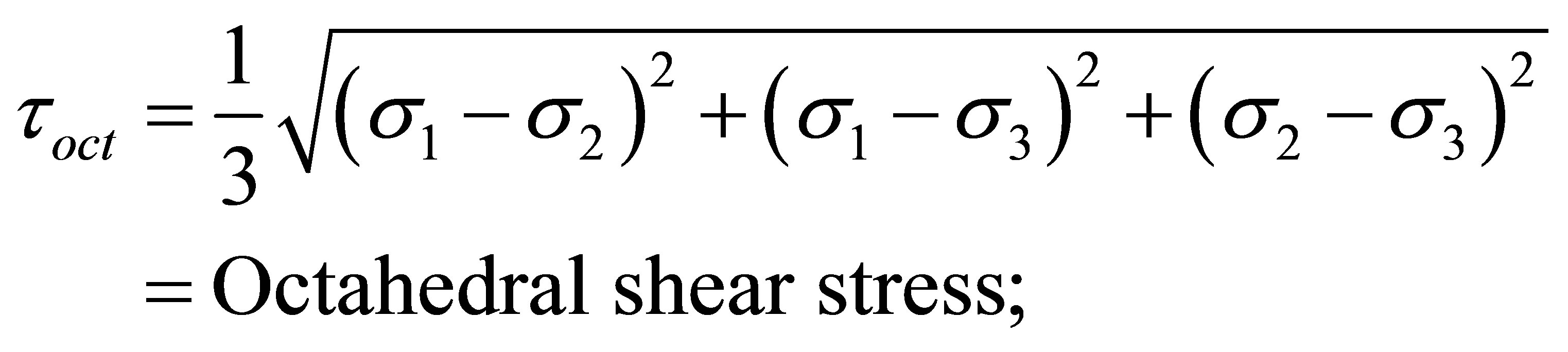
k1, k2 and k3 regression constants.
A general form for these proposed models is the Andrei model (1999 [18]):
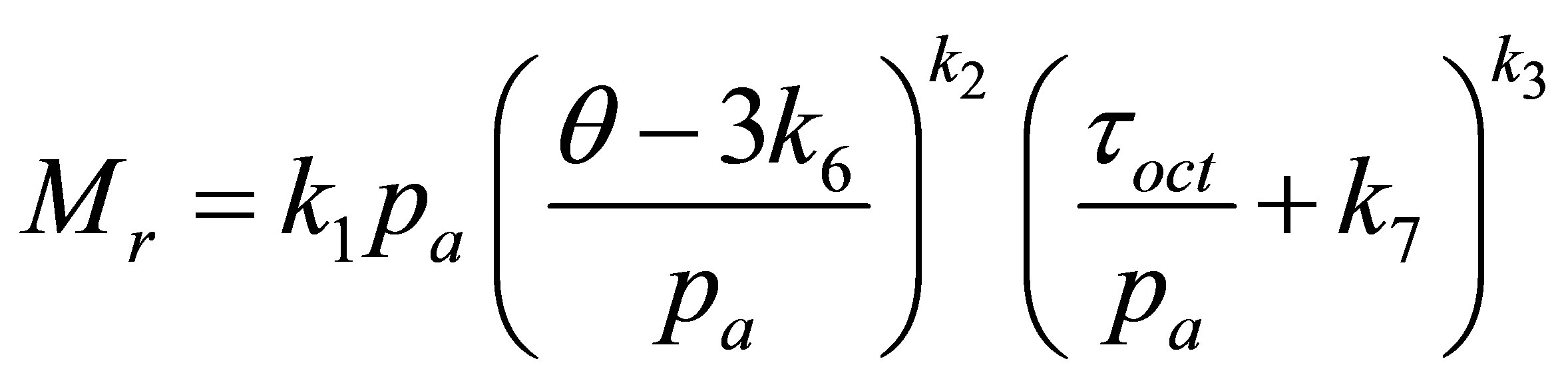 (5)
(5)
k1 − k7 = regression constants.
The Andrei model (1999 [18]) was then adopted by the National Highway Research Program (NCHRP, 2004) [2] in its simplified version (k6 = 0 and k7 = 1).
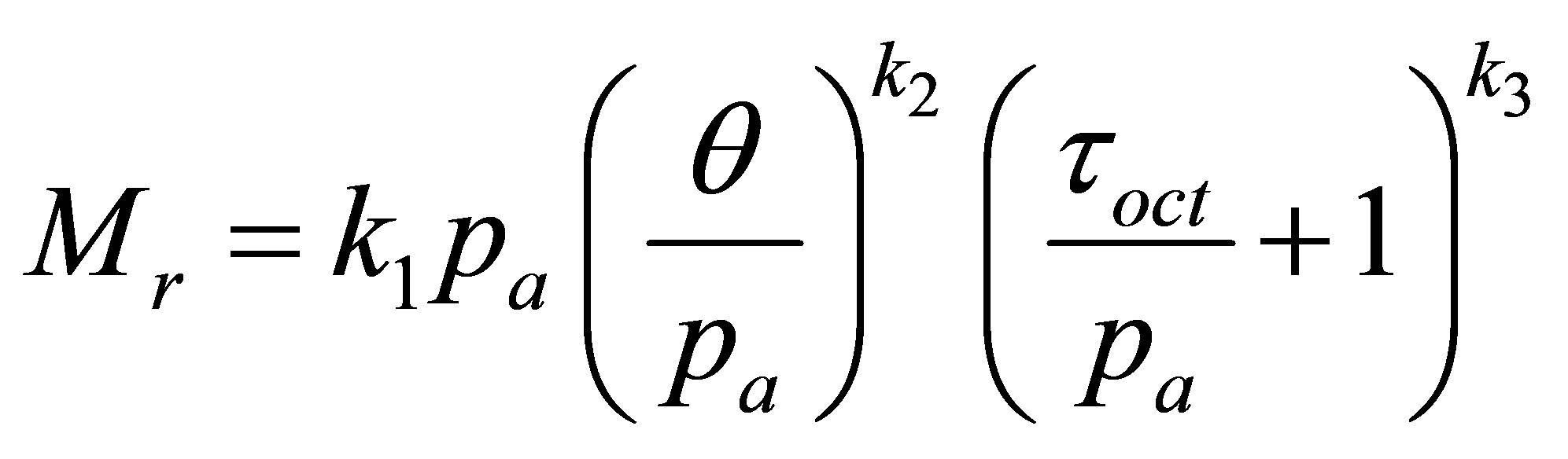 (6)
(6)
k1, k2 and k3, regression constants.
It is worth noting that gravel lateritic soils consisted of soft and hard concretions as well as quartzites in a matrix consisting of fines particles composed of a mixture of clays and graves. Therefore, both the Uzan-Witczack model (1988 [1]) and the NCHRP one (2004 [2]) which can be adapted to the fine soils as well as to the granular soils seem to well fit with gravel lateritic soils that are located between these two types of material. These two models were so retained for correlation studies.
Correlations with Uzan-Witczack (1988) [17] and NCHRP (2004) Models [2]
The results of the correlations of the resilient modulus for Uzan-Witczack (1988 [1]) and NCHRP (2004 [2]) models are presented below (Tables 6 and 7). It is observed that the found coefficients of regression are very close to 1 (between 0.902 and 0.999). This observation means that both models give very good correlations of the resilient modulus and can be used to model the resilient behaviour of gravel lateritic soils. However, the comparison by box-diagram of the values of regression coefficients of both models (Figure 10) showed that the Uzan-Witczack model (1988 [1]) give better correlations than the NCHRP model (2004 [2]).
5. Conclusions
Cyclic triaxial tests made on gravels lateritics soils allowed to have a number of very important results.
The study of the cyclic behavior of gravel lateritic soils confirms the importance of the effect of stress level on resilient modulus. Indeed, resilient modulus decreases inversely with the increase of bulk and deviatoric stress. However, the effect of cement percentage on the increase
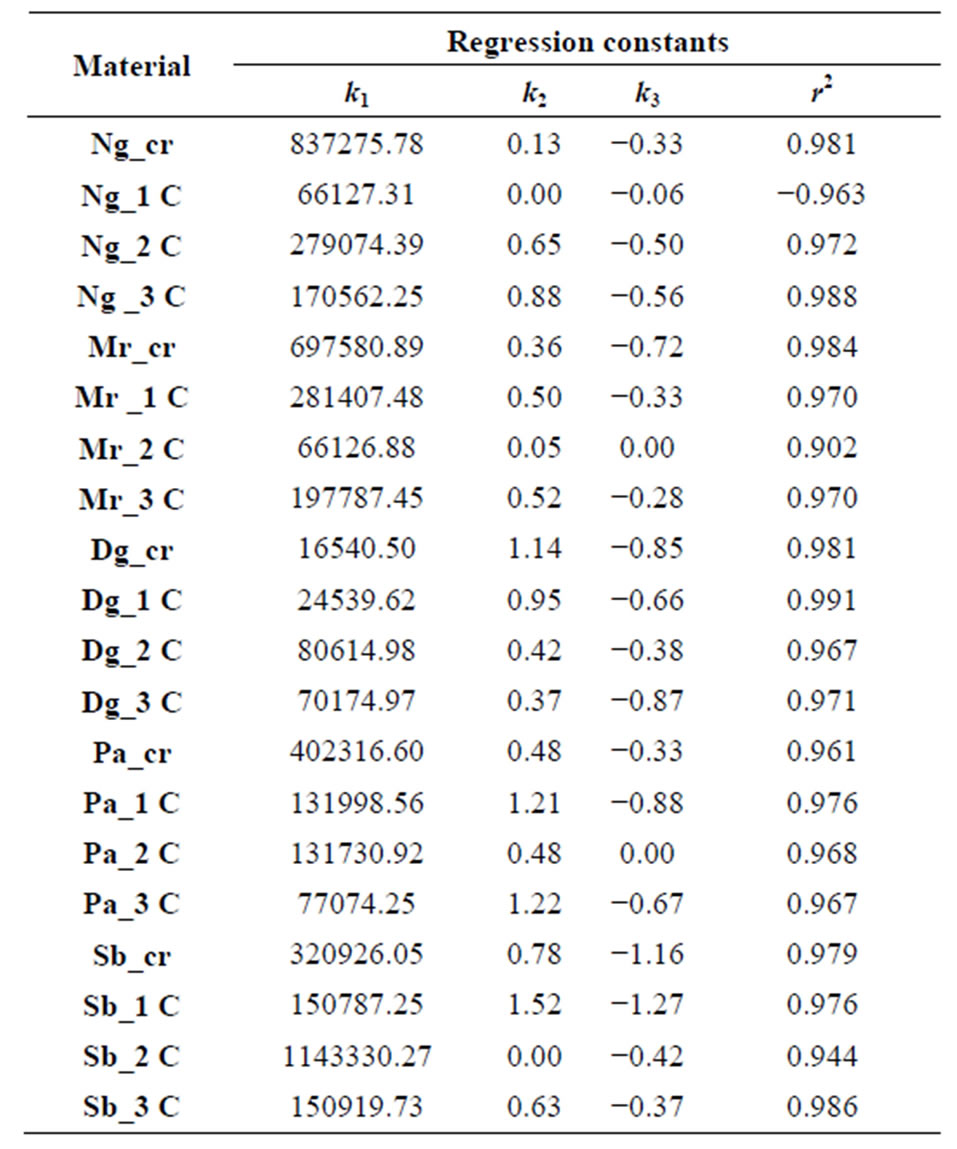
Table 6. Coefficients ki and r2 obtained with Uzan-Witczack model (1988) [1].
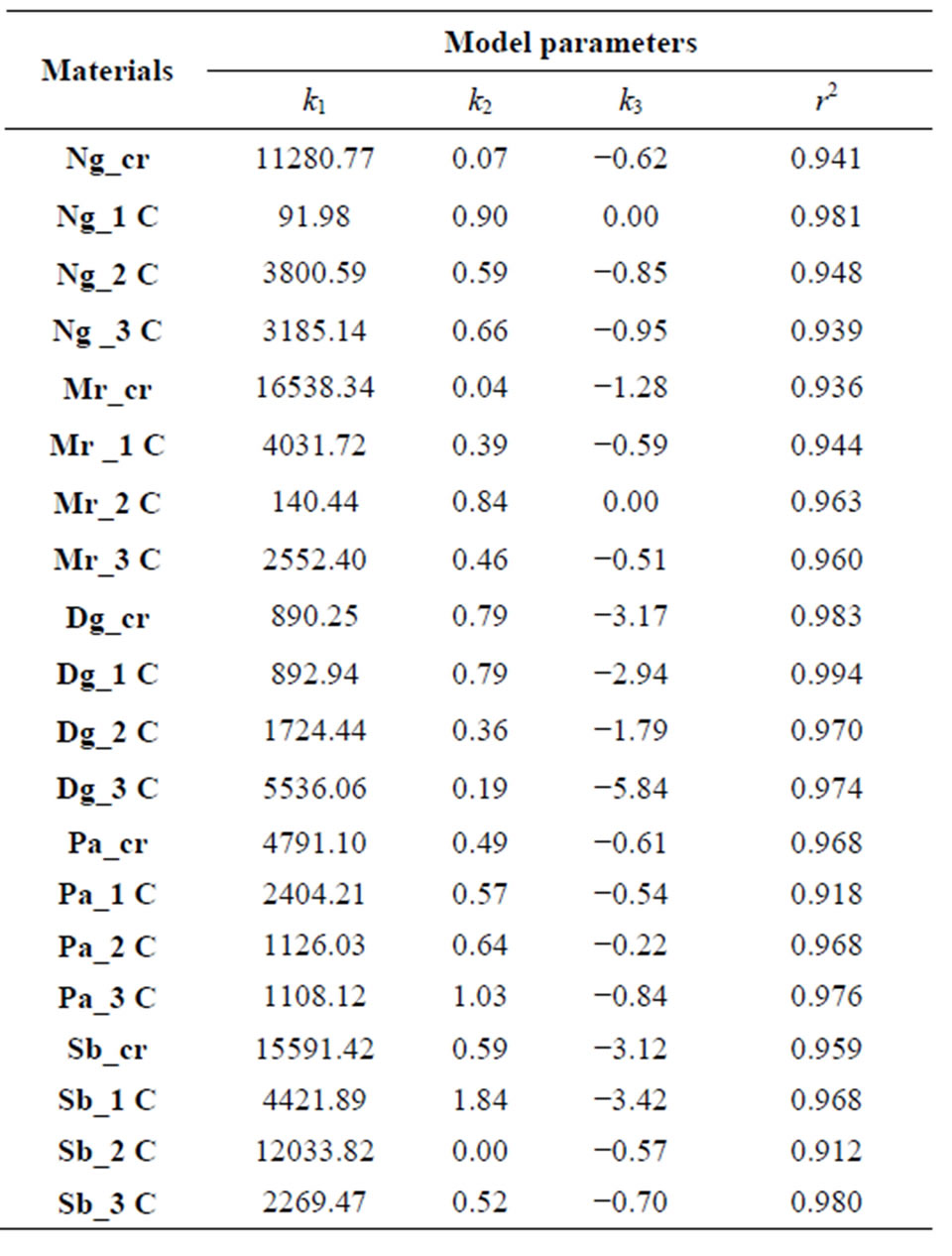
Table 7. Coefficients ki and r2 obtained with the NCHRP (2004) [2] model.
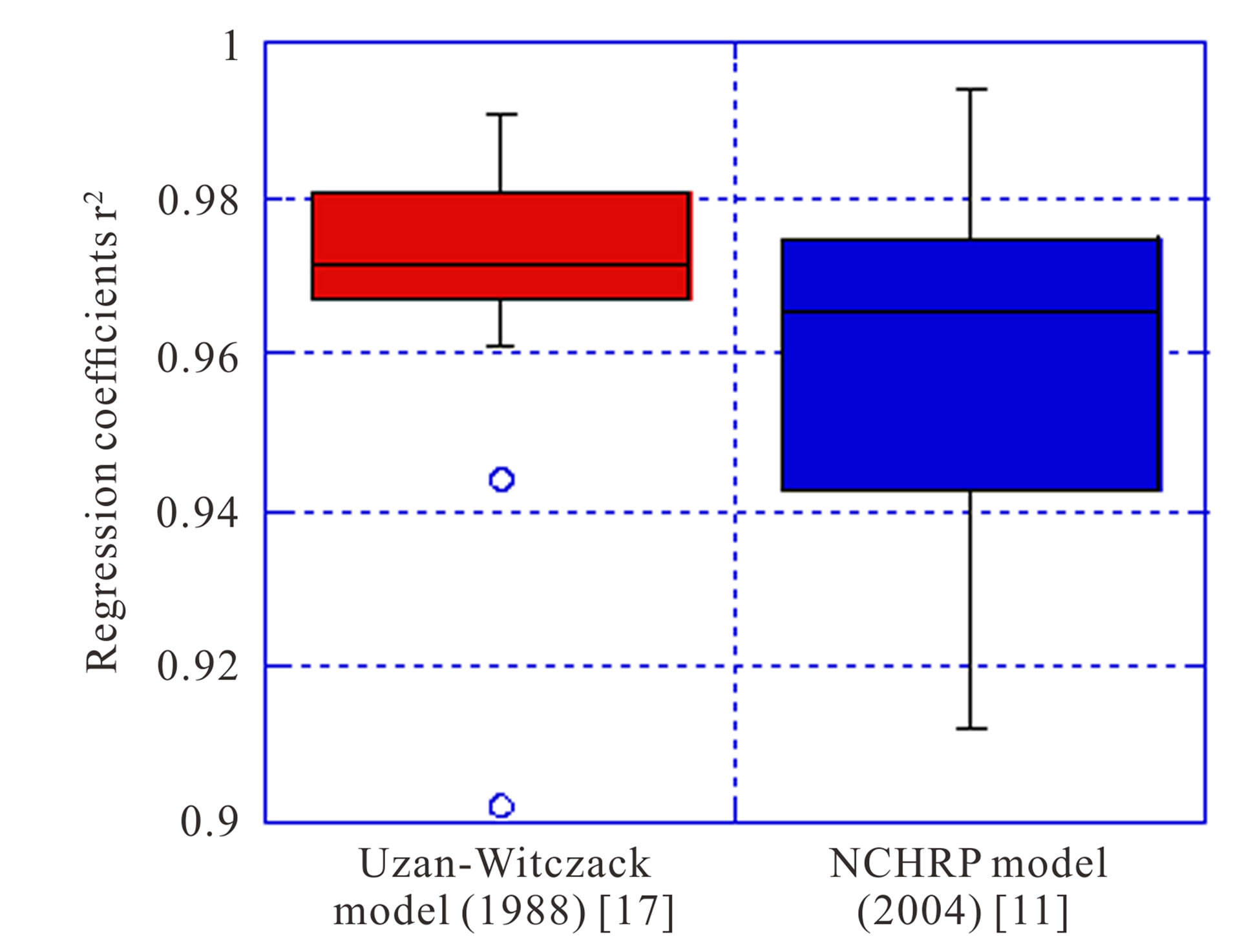
Figure 10. Comparison of the models coefficients of correlation.
of the stiffness of the material is not confirmed for all the materials and differs from one gravel to another. On the other hand, the effect of the moisture content seems to affect the values of the resilient modulus in a sensitive way.
These results play a key important role in the prediction of the behaviour model of resilient modulus of gravel lateritic soils. Indeed, the Uzan-Witczack (1988) [1] and the NCHRP model (2004) [2] had allowed very good correlations with better results with the first one. These models can be used for finite element modelling of pave- -ments.
6. Acknowledgements
The authors of the article would like to thank Dr Makhaly BA and would like to appreciate his important contribution for some of the gravel lateritic tests which have been realised in Wisconsin University of Madison.
REFERENCES
- M. W. Witczack and J. Uzan, “The Universal Airport Pavement Design System, Report I of IV: Granular Material Characterization,” University of Maryland, College Park, Md., 1988.
- NCHRP, “Laboratory Determination of Resilient Modulus for Flexible Pavement Design,” National Cooperative Highway Research Program (NCHRP) Project 1-28A, Transportation Research Board of National Academies, 2004.
- M. S. Samb, “Caractérisation des Complexes Latéritegéotextile pour le Renforcement des Remblais,” Mémoire M. Ing., Transport, Université de Montréal, 1986.
- M. Fall, “Identification et Caractérisation Mécanique de Graveleux Latéritiques du Sénégal: Application au Domaine Routier,” Thèse de Doctorat INPL, ENSGN, 1993.
- M. Fall, A. Sawangsuriya, C. H. Benson, T. B. Edil and P. J. Bosscher, “On the Investigations of Resilient Modulus of Residual Tropical Gravel Lateritic Soils from Senegal (West Africa),” Geotechnical and Geological Engineering Journal, Vol. 26, No. 1, 2008.
- E. J. Yoder and M. W. Witczak, “Principles of Pavement Design,” 2nd Edition, Wiley, New York, 1975.
- J. L. Paute, P. Hornych and J. P. Benaben, “Comportement Mécanique des Graves non Traitées,” Bulletin de Liaison des Laboratoires des Ponts et Chaussées No. 190, Marsavril, 1994, pp. 27-55.
- J. Martinez, “Contribution au Dimensionnement Rationnel des Structures de Chaussées Souples et Inverses. Comportement des Graves non Traitées et des sols Support,” Thèse Doctorat d’État, université Montpellier II, 1990.
- T. C. Hopkins, T. L. Beckham and C. Sun, “Resilient Modulus of Compacted Crushed Stone Aggregate Bases,” Research Report KTC-05-27/SPR-229-01-1F, Kentucky Transportation Center, College of Engineering, University of Kentucky, 2007, p. 89.
- M. Bâ, “Comportement Mécanique sous Sollicitations Cycliques de Granulats Quartzitiques de Bakel—Comparaison avec des Matériaux de Référence du Sénégal et d’Amérique (USA),” Thèse de Doctorat Géotechnique routière, UCAD, Faculté des Sciences et Techniques, 2012.
- G. T. Williams, “Stress/Strain Relationships of Granular Soils,” Thornton Report R 1297, “Shell” Research Limited, 1963.
- P. Kolisoja, “Resilient Deformation Characteristics of Granular Materials,” Ph.D. thesis, Tampere University of Technology, Publ. No. 223, Tampere, 1997.
- F. Lekarp, U. Isacsson and A. Dawson, “State of the Art. I: Resilient Response of Unbound Aggregates,” Journal of Transportation Engineering, Vol. 126, No. 1, 2000, pp. 66-75.
- H. B. Seed, F. G. Mitry, C. L. Monismith and C. K. Chan, “Prediction of Flexible Pavement Deflections from Laboratory Repeated Load Tests,” NCHRP Rep. No. 35, National Cooperative Highway Research Program, 1967.
- S. F. Brown and P. S. Pell, “An Experimental Investigation of the Stresses, Strains and Deflections in a Layered Pavement Structure Subjected to Dynamic Loads,” Proceedings of the 2nd International Conference on Concrete Pavement Design, 1967, pp. 487-504.
- R. G. Hicks and C. L. Monismith, ‘‘Factors Influencing the Resilient Properties of Granular Materials,’’ Hwy. Res. Rec. Vol. 345, 1971, pp. 15-31.
- J. Uzan, “Characterization of Granular Material,” Transp. Res. Rec. 1022, Transportation Research Board, Washington, D.C., 1985, pp. 52-59.
- D. Andrei, “Development of a Harmonized Test Protocol for the Resilient Modulus of Unbound Materials Used in Pavement Design,” M.S. Thesis, University of MarylandCollege Park, 1999.

