American Journal of Computational Mathematics
Vol.05 No.03(2015), Article ID:59361,7 pages
10.4236/ajcm.2015.53026
An Accurate Numerical Integrator for the Solution of Black Scholes Financial Model Equation
Iyakino P. Akpan1*, Johnson O. Fatokun2
1Department of Basic Science, College of Agriculture, Lafia, Nigeria
2Department of Mathematical Science and Information Technology, Federal University, Dutsin-Ma, Nigeria
Email: *akpanip@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 May 2015; accepted 29 August 2015; published 2 September 2015
ABSTRACT
In this paper the Black Scholes differential equation is transformed into a parabolic heat equation by appropriate change in variables. The transformed equation is semi-discretized by the Method of Lines (MOL). The evolving system of ordinary differential equations (ODEs) is integrated numerically by an L-stable trapezoidal-like integrator. Results show accuracy of relative maximum error of order 10−10.
Keywords:
Black Scholes Equation, Partial Differential Equations (PDEs), Method of Lines (MOL), L-Stable Trapezoidal-Like Integrator

1. Introduction
Financial derivative, in particular options, became very popular financial contracts in the last few decades. Options can be used to hedge assets and portfolios in order to control the risk due to movements in the share price. A European call (put) option provides the right share price to buy or sell a fixed number of assets at the fixed exercised price E, at the expiry time t0 [1] . In the early 1970’s Fisher Black and Myron Scholes made a major breakthrough by deriving a partial differential equation that must be satisfied by the price of any derivative security dependent on a non-dividend-paying stock [2] . According to [3] their work had a huge impact on how options were viewed in the financial world. In an idealized financial market, the price of a European option can be obtained as the solution of the Black-Scholes equation [4] [5] . However, the Black Scholes equation has been derived under quite restrictive assumptions such as frictionless, liquid and complete market. In recent years nonlinear Black Scholes equations have been derived in order to model transaction costs arising in the hedging of portfolios [1] [6] [7] and feedback effects due to large traders [8] - [13] .
In seeking the solution of the Black Scholes equation, emphasis is always laid on derivation of formula or equation for the price of the option of interest and computation of the price of the option. This calls for the usage of numerical methods because explicit theoretical solutions for the price of the option do not exist. From a binomial model, [6] derived an option price that takes into account transaction costs which approximates a Black Scholes price but with modified volatility. [14] [15] computed the option price of the Black Scholes equation as the solution of a nonlinear quasi-variational inequality. This approach has the disadvantage that the option price depends on the choice of the utility function. Seeking the analytical solution of the Black-Scholes equation, [16] used the Adomain decomposition method. Adomain decomposition can provide analytical approximations to a wide class of linear and nonlinear equations without perturbation, closure approximations or discretization. Solution for the Black-Scholes equation as a semigroup on spaces of continuous functions on (0, ∞) is presented in [17] .
In the mathematical literature, only a few results can be found on the numerical discretization of Black Scholes equations. The numerical approaches vary from binomial approximations for American options in stochastic framework [18] , Monte-Carlo methods [19] , finite element discretization [20] , and finite difference approximations [1] . The numerical discretization of the Black Scholes equations with nonlinear volatilities has been performed using explicit finite difference schemes [21] [22] . Explicit numerical schemes have the disadvantage that restrictive conditions on the discretization parameters, time and space steps, are needed to obtain stable, convergent schemes [23] . Moreover the convergence order is the only one in time.
The Method of Lines (MOL) is a general procedure for the solution of time-dependent partial differential equations (PDEs) [24] . The basic idea of the MOL is to replace the spatial (boundary value) derivatives in the PDEs with algebraic approximations [25] . Ones this is done, the spatial derivatives are no longer stated explicitly in terms of the spatial dependent variables. Thus, only the initial value variable, typically time in a physical problem, remains, which results in a system of ODEs that approximates the original PDE. An accurate integration algorithm for initial value ODEs to compute an approximate numerical solution to the PDE can then be used for the numerical integration. One of the salient features of the MOL is the use of existing, and generally well established, numerical methods for ODEs [26] .
This paper is organized thus: In Section 2 we transform the black Scholes equation into a heat equation by change in variables. In Section 3 we introduce an L-stable trapezoidal like integrator for the numerical integration of the transformed Black Scholes equation. Section 4 is devoted to the numerical test of the method on the transformed Black Scholes equation. Section 5 explains the computation of the errors and relative errors of the method while results are discussed in Section 6.
2. Transforming the Black Scholes Equation into a Parabolic Heat Equation
Given the Black Scholes equation:
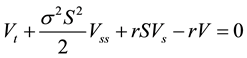 (1)
(1)
Subject to:
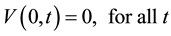 (2a)
(2a)
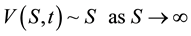 (2b)
(2b)
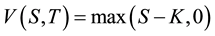 (2c)
(2c)
where:
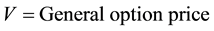 (3a)
(3a)
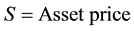 (3b)
(3b)
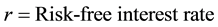 (3c)
(3c)
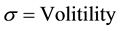 (3d)
(3d)
Following [27] to transform the diffusion-advection-reaction Equation (1) into a parabolic heat PDE, we make the following change of variables:
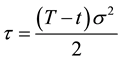 (4a)
(4a)
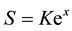 (4b)
(4b)
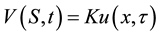 (4c)
(4c)
By taking appropriate partial derivatives of
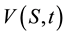 in Equation (4c) and substituting in Equation (1) yields
in Equation (4c) and substituting in Equation (1) yields
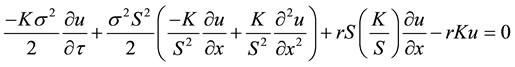 (5)
(5)
Substituting
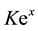 for
for
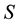 in Equation (5) and dividing by
in Equation (5) and dividing by
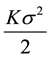 yields
yields

Defining

And substituting for k in Equation (6) we obtain

By defining

Then, the partial derivatives of




Making





Substituting Equations (13), (14) and (15) into Equation (8) we obtain

By letting the coefficients of


Under the condition that

and

the Black Scholes equation given in Equation (1) is transformed into the parabolic heat equation PDE

Subject to


According to [28] European Call option as the solution to the Black Scholes equation on


Equating both hand sides of Equation (21) yields

Substituting for S from Equation (4) in Equation (22) gives

Substituting



By equating the RHS of Equations (2b) and (24)

Substituting



Substituting Equation (26) for


Remark
By appropriate change in variables, Equation (1) is transformed into Equation (19) which is a parabolic heat equation to be discretized by the MOL. Equation (27) is the derived approximate theoretical solution to the transformed Black Scholes equation.
3. L-Stable Implicit Trapezoidal-Like Integrator
The trapezoidal-like integrator

where





The derivation of the method (28) and the analysis of the order of accuracy are as discussed in [29] , while the stability properties of the method are discussed in [30] .
4. Numerical Experimentation
For numerical experimentation the following values were used: k = 0.001, r = 0.1, σ = 0.2, K = 100, T = 1, Δx = 0.01 and Δτ = 0.001.
5. Computation of Absolute and Relative Errors
In this section we explain how the absolute errors and relative errors of the methods shown in Table 1 and Table 2 were obtained.
Table 1. Solution approximations and errors of the new scheme.
Figure 1. The graphs of the numerical solution of the new scheme and the theoretical solution.
Table 2. Solution approximations, errors and relative errors of the new scheme.
5.1. Absolute Errors
The absolute errors of the scheme were computed by the use of the formula:
where the numerical solution at the grid point



5.2. Relative Errors
Relative errors of the method were computed by use of the formula:
where the numerical solution at the grid point



6. Results and Discussion
On the implementation of the L-stable trapezoidal-like integrator for the solution of transformed Black Scholes equation after discretizing with MOL, the errors and relative errors of the scheme were computed as shown in Table 1 and Table 2 respectively. The trapezoidal-like integrator is an accurate time predictor of the solution of the Black Scholes equation. All computations in this paper were carried out in Maple 15 while the plotting of Figure 1 was carried out in Matlab.
Cite this paper
Iyakino P.Akpan,Johnson O.Fatokun, (2015) An Accurate Numerical Integrator for the Solution of Black Scholes Financial Model Equation. American Journal of Computational Mathematics,05,283-290. doi: 10.4236/ajcm.2015.53026
References
- 1. Dewynne, J., Howison, S. and Wilmott, P. (1995) Option Pricing: Mathematical Models and Computation. Financial Press, Oxford.
- 2. Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-659.
http://dx.doi.org/10.1086/260062 - 3. Kangro, R. (2011) Computational Finance.
http://www.math.ut.ee/~rkangro/computational_finance/finmat11/_eng_11.pdf - 4. Bensaid, B., Lesne, J., Pages, H. and Scheinkman, J. (1992) Derivative Asset Pricing with Transaction Costs. Math. Finance, 2, 63-86.
http://dx.doi.org/10.1111/j.1467-9965.1992.tb00039.x - 5. Merton, R.C. (1973) Theory of Rational Option Pricing. Bell Journal of Economics and Management Science, 4, 141-183.
http://dx.doi.org/10.2307/3003143 - 6. Boyle, P. and Vorst, T. (1973) Option Replication in Discrete Time with Transaction Costs. Journal of Finance, 47, 271-293.
http://dx.doi.org/10.1111/j.1540-6261.1992.tb03986.x - 7. Davis, M., Panis, V. and Zariphopoulou, T. (1993) European Option Pricing with Transaction Fees. SIAM Journal on Control and Optimization, 31, 470-493.
http://dx.doi.org/10.1137/0331022 - 8. Frey, R. (1998) Pefect Option Hedging for a Large Trader. Finance and Stochastics, 2, 115-141.
- 9. Frey, R. (2000) Market Illiquidity as a Source of Model Risk in Dynamic Hedging. In: Gibson R., Ed., Model Risk, RISK Publications, London.
- 10. Genotte, G. and Leland, H. (1990) Market Liquidity, Hedging and Crashes. American Economic Review, 80. 999-1020.
- 11. Jarrow, R. (1992) Market Manipulation, Bubbles, Corners and Short Squeezes. Journal of Financial and Quantitative Analysis, 27, 311-336.
http://dx.doi.org/10.2307/2331322 - 12. Platen, E. and Schweizer, M. (1998) On Feedback Effects from Hedging Derivatives. Mathematical Finance, 8, 67-84.
http://dx.doi.org/10.1111/1467-9965.00045 - 13. Schonbucher, P. and Wilmot, P. (2000) The Feedback Effect of Hedging in Illiquid Markets. The SIAM Journal on Applied Mathematics, 61, 232-272.
http://dx.doi.org/10.1137/S0036139996308534 - 14. Hodges, S.D. and Neuberger, A. (1989) Optimal Replication of Contingent Claims under Transaction Costs. Review of Futures Markets, 8, 222-239.
- 15. Whalley, A.E. and Wilmot, P. (1997) An Asymptotic Analysis of an Optimal Hedging Model for Option Pricing with Transaction Costs. Mathematical Finance, 7, 307-324.
http://dx.doi.org/10.1111/1467-9965.00034 - 16. Bohner, M. and Zheng, Y. (2009) On Analytical Solutions of the Black-Scholes Equation. Applied Mathematics Letters, 22, 309-313.
http://dx.doi.org/10.1016/j.aml.2008.04.002 - 17. Emamirad, H., Goldstein, G.R. and Goldstein, J.A. (2012) Chaotic Solution for the Black-Scholes Equation. Proceedings of American Mathematical Society, 140, 2043-2052.
http://dx.doi.org/10.1090/S0002-9939-2011-11069-4 - 18. Lamberton, D. (1998) Error Estimates for the Binomial Approximation of American Put Options. The Annals of Applied Probability, 8, 206-233.
http://dx.doi.org/10.1214/aoap/1027961041 - 19. Lai, Y. and Spainer, J. (1998) Applications of Monte Carlo/Quasi-Monte Carlo Methods in Finance: Option Pricing. Springer, Berlin.
- 20. Pironneau, O. and Hecht, F. (2000) Mesh Adaption for Black and Scholes Equations. East-West Journal of Numerical Mathematics, 8, 25-35.
- 21. Paras, A. and Avellanneda, M. (1994) Dynamic Hedging Portfolios for Derivative Securities in the Presence of Large Transaction Costs. Applied Mathematical Finance, 1, 165-193.
http://dx.doi.org/10.1080/13504869400000010 - 22. Goldstein, J.A., Mininni, R.M. and Romanelli, S. (2008) A New Explicit Formula for the Solution of the Balck-Merton-Scholes Equation. In: Sengupta, A. and Sundar, P., Eds., Infinite Dimensional Stochastic Analysis, World Scientific, Singapore, 226-235.
http://dx.doi.org/10.1142/9789812779557_0013 - 23. Strikwerda, J.C. (1989) Finite Difference Schemes and Partial Differential Equations (Wadsworth & Brooks/Cole Mathematics Series). Wadsworth & Brooks/Cole Advanced Books & Software, Pacific Grove.
- 24. Schiesser, W.E. (1991) The Numerical Method of Lines: Integration of Partial Differential Equations. Academic Press, San Diego.
- 25. Haq, S., Hussain, A. and Uddin, M. (2011) RBFs Meshless Method of Lines for the Numerical Solution of Time-Dependent Nonlinear Coupled Partial Differential Equations. Applied Mathematics, 2, 414-423.
http://www.sciRP.org/journal/am
http://dx.doi.org/10.4236/am.2011.24051 - 26. Lambert, J.D. (1993) Numerical Methods for Ordinary Differential Systems. John Wiley, Chichester.
- 27. Coppex, F. (2009) Solving Black Scholes Equation: A Demystification.
www.francoidcoppe.com/blackscholes.pdf - 28. Ankudinova, J. and Ehrhardt, M. (2007) On the Numerical Solution of Nonlinear Black Scholes Equations.
http://www-amna.math.uni-wuppertal.de/~ehrhardt/papers/nonlinearBS - 29. Fatokun, J.O. and Akpan, I.P. (2013) L-Stable Implicit Trapezoidal-Like Integrators for the Solution of Parabolic Partial Differential Equations on Manifolds. African Journal of Mathematics and Computer Science Research, 6, 183-190.
http://www.academicjournals.org/ajmcsr - 30. Fatokun, J.O. and Akpan, I.P. (2014) A Trapezoidal-Like Integrator for the Numerical Solution of One-Dimensional Time Dependent Schrodinger Equation. American Journal of Computational Mathematics, 4, 271-279.
http://dx.doi.org/10.4236/ajcm.2014.44023
NOTES
*Corresponding author.






