American Journal of Computational Mathematics
Vol.04 No.04(2014), Article ID:49507,27 pages
10.4236/ajcm.2014.44029
Conservative Interaction of N Internal Waves in Three Dimensions
Victor A. Miroshnikov
Department of Mathematics, College of Mount Saint Vincent, New York, USA
Email: victor.miroshnikov@mountsaintvincent.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 July 2014; revised 6 August 2014; accepted 13 August 2014
ABSTRACT
The Navier-Stokes system of equations is reduced to a system of the vorticity, continuity, Helmholtz, and Lamb-Helmholtz equations. The periodic Dirichlet problems are formulated for internal waves vanishing at infinity in the upper and lower domains. Stationary kinematic Fourier (SKF) structures, stationary exponential kinematic Fourier (SKEF) structures, stationary dynamic exponential (SDEF) Fourier structures, and SKEF-SDEF structures of three spatial variables and time are constructed in the current paper to treat kinematic and dynamic problems of the three-di- mensional theory of the Newtonian flows with harmonic velocity. Two exact solutions for conservative interaction of N internal waves in three dimensions are developed by the method of decomposition in invariant structures and implemented through experimental and theoretical programming in Maple™. Main results are summarized in a global existence theorem for the strong solutions. The SKEF, SDEF, and SKEF-SDEF structures of the cumulative flows are visualized by two-parametric surface plots for six fluid-dynamic variables.
Keywords:
Existence Theorem, Internal Waves, Invariant Structures, Experimental Programming, Theoretical Programming

1. Introduction
The three-dimensional (3d) Navier-Stokes system of partial differential equations (PDEs) for a Newtonian fluid with a constant density
 and a constant kinematic viscosity
and a constant kinematic viscosity
 in a gravity field
in a gravity field
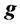 is
is
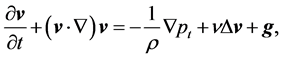 (1)
(1)
 (2)
(2)
where
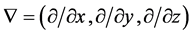 and
and
 are the gradient and the Laplacian in the Cartesian coordinate system
are the gradient and the Laplacian in the Cartesian coordinate system
 of the 3d space with unit vectors
of the 3d space with unit vectors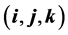 ;
;
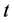 is time;
is time;
 is a vector field of the flow velocity;
is a vector field of the flow velocity;
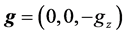 is a vector field of the gravitational acceleration;
is a vector field of the gravitational acceleration;
 is a scalar field of the total pressure.
is a scalar field of the total pressure.
By a flow vorticity
 of the velocity field
of the velocity field
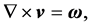 (3)
(3)
Equation (1) may be written into the Lamb-Pozrikidis form [1] [2]
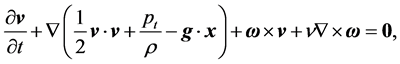 (4)
(4)
which sets a dynamic balance of inertial, potential, vortical, and viscous forces, respectively.
Using a dynamic pressure per unit mass [3]

where




and the vortex force


Equation (4) is reduced to the Lamb-Helmholtz PDE [5]

for a scalar Bernoulli potential and a vector Helmholtz potential


where




shows that a virtual force



The exponential Fourier eigenfunctions were calculated by separation of variables of the 3d Laplace equation, for instance, see [1] and [4] , and applied for a linear part of the kinematic problem for free-surface waves in the theory of the ideal fluid with

In the current paper, the SKF, SKEF, SDEF, and SKEF-SDEF structures are extended in three dimensions to examine kinematic and dynamic problems for internal conservative waves in the theory of Newtonian flows with harmonic velocity. The structure of this paper is as follows. The SKF structures are used to compute theoretical solutions for the velocity components in Section 2. Theoretical solutions for the kinematic potentials of the velocity field and the dynamic potentials of the Navier-Stokes PDE are obtained in Sections 3 and 4, respectively, through the SKEF structures. The SDEF structures are constructed in Section 5. In Section 6, the SDEF and SKEF-SDEF structures are used for theoretical computation of the kinetic energy and the dynamic pressure. Decomposition of harmonic variables in a SKEF structural basis is tackled in Section 7. Verification of the experimental and theoretical solutions by the Navier-Stokes system of PDEs and the existence theorem are provided in Section 8. Discussion of significant outcomes and visualization of the developed structures are given in Section 9, which is followed by a summary of main results in Section 10.
2. Velocity Components in the SKF Structures
The following theoretical solutions and admissible boundary conditions of Sections 2-8 were primarily computed in Maple™ using experimental programming with lists of equations and expressions for numerical indices and N = 3 in the virtual environment of a global variable Eqe by 33 developed procedures of 1748 code lines.
Theoretical problems for harmonic velocity components











To consider conservative interaction of N internal waves, the cumulative flows are decomposed into superposi- tions of local flows

such that the local vorticity and continuity equations are




where
An upper cumulative flow is specified by a Dirichlet condition, which is periodic in the x- and y-directions, through the two-dimensional (2d) SKF structure on a lower boundary




and a vanishing Dirichlet condition in the z-direction

A lower cumulative flow is identified by a periodic Dirichlet condition on an upper boundary



and a vanishing Dirichlet condition in the z-direction

Thus, an effect of surface waves on the internal waves is described by the Dirichlet conditions (23) and (25). While notations of boundary coefficients


is used for kinematic structural functions





The experimental solutions show that similar to [5] , boundary conditions for




Figure 1. Configuration of upper and lower domains for conservative waves.
Similarly to w, u and v vanish as

for the upper and lower cumulative flows, respectively.
Theoretical solutions of (14)-(26) are constructed in the SKF structure



where first letters f, q, g, r of space-dependent structural coefficients



Computation of spatial derivatives of




Application of (32)-(34) to (31) and substitution in (19)-(22) reduce the four PDEs to three ordinary differential equations (ODEs) and an algebraic equation (AE). For these equations to be satisfied exactly for all independent variables, independent parameters, structural functions, and structural coefficients of the local flows x, y, z, t,









In these four separated systems, first and second equations, which are produced by (19) and (20), are ODEs; third equations, which are generated by (21), are AEs; and fourth equations, which are created by (22), are again ODEs.
Solving the third AEs of separated systems (35)-(38) yields functional relations between structural coefficients:

Substitution of (39) in the second ODEs and addition/subtraction of the first ODEs reduces the second ODEs to identities. Substitution of functional relations (39) into the fourth ODEs reduces them to the following system:

Construct solutions of the first and fourth ODEs in stationary exponential (SE) structures with the following general terms:

where


Substitution of (41) into (40) returns admissible values of


Finally, substitutions of (39) and (41)-(43) into (31) and (18) give the following velocity components of the upper and lower cumulative flows, respectively:

Thus, the velocity components are resolved through the 3d SKEF structures. If




where




where
Therefore, structural parameters of (44)

return cosine and sine of local front angles




In the case of resonance propagation with

3. Kinematic Potentials through the SKEF Structures
Theoretical problems for the kinematic potentials










since a scalar-vector duality the velocity field admits two descriptions: a scalar description





The local kinematic potentials are governed by local Helmholtz PDEs







where
The periodic Dirichlet conditions for

boundary


of a lower domain


where



Construct general terms of the kinematic potentials of the upper and lower flows in the SKF structures by

Computation of derivatives of (65) by (32)-(34) and substitution in (57)-(63) reduce the seven Helmholtz PDEs to four Helmholtz ODEs and three Helmholtz AEs. For these equations to be satisfied exactly for all independent variables, independent parameters, structural functions, boundary coefficients, and structural coefficients of the upper and lower flows x, y, z, t,

For








where first and second ODEs are produced by (57)-(58), third AEs are generated by (59), and fourth ODEs are created by (60).
For





where first and second AEs are produced by (61)-(62) and third ODEs are generated by (63).
Solving the third AEs of separated systems (66)-(69) yields functional relations between structural coefficients

Substitution of (74) in the second ODEs of (66)-(69) and addition/subtraction of the first ODEs reduces the second ODEs to identities. Substitution of (74) into the fourth ODEs reduces them to the following system:

Solving the first AEs of separated systems (70)-(73) gives structural coefficients

Substitution of (76) in the second AEs and third ODEs of (70)-(73) reduces them to identities.
Construct solutions of the first ODEs of (66)-(69) and (75) in the SE structures with the following general terms for the upper and lower flows, respectively,

where









Substitution of (77) and (78) into (75) reduces them to identities.
Finally, substitutions of (74), (76)-(78) into (65) and (56) give the following kinematic potentials in the SKEF structures for the upper and lower cumulative flows, respectively,

where structural coefficients are given by (78) and


When



When



4. Dynamic Potentials through the SKEF Structures
Definitions of the dynamic vector potential (the Helmholtz potential)



Theoretical problems for the dynamic scalar potential (the Bernoulli potential)


Since the cumulative dynamic potentials are decomposed into superpositions of local dynamic potentials

the local dynamic potentials are governed by three definitions and three Lamb-Helmholtz PDEs




where




Construct a general term of the Bernoulli potential in the SKF structure by

and the SKEF structure




Computation of temporal and spatial derivatives of





Application of (93) to (87) and (79) gives the following Helmholtz potentials in the SKEF structures for the upper and lower cumulative flows, respectively,

where structural coefficients are



Computation of derivatives of (97) and (91) by (94)-(96) and (32)-(34), respectively, and substitution in (88)- (90) reduce the three Lamb-Helmholtz PDEs to two Lamb-Helmholtz AEs and one Lamb-Helmholtz ODE. For these equations to be satisfied exactly for all independent variables, independent parameters, structural functions, boundary coefficients, and structural coefficients of the upper and lower flows x, y, z, t,






where first and second AEs are produced by (88)-(89) and third ODEs are generated by (90).
Solving the first AEs of separated systems (101)-(104) gives the following Bernoulli potentials in the SKEF structures for the upper and lower cumulative flows, respectively,

where structural coefficients are

Substitution of (106) in the second AEs and third ODEs of (101)-(104) reduces them to identities. The Bernoulli potential (105)-(106) does not depend on boundary coefficients of the kinematic potentials






In the scalar description,


where



where


since an integration constant again vanishes for the SKEF structures in agreement with (24) and (26). Therefore, computation of be by (110), (79), and (93) also results in (105)-(106).
5. Stationary Dynamic Exponential Fourier (SDEF) Structures
By the generalized Einstein notation for summation that is extended for exponents in [5] , define two SKEF structures





Following the experimental solutions, construct 16 trigonometric structural functions of the SDEF structure

where capital letters C and S stand for cosine and sine, letters s and d for sum and difference of arguments



Computation of a general term



where structural coefficients are

A general term


where structural coefficients are

Conversion of (115)-(116) by triangular summation of non-diagonal terms and addition of (113)-(114) yields summation formulas for the product of the SKEF structures written through the SDEF structures for the upper and lower flows, respectively,

where 9 diagonal structural coefficients are given by (114) and 16 non-diagonal structural coefficients are

6. Total Pressures through the SKEF-SDEF Structures
The kinetic energy per unit mass of the upper and lower cumulative flows,

is computed as a superposition of three products of the SKEF structures for the velocity components that are converted from the functional form (44) to the structural form (92) for the upper and lower cumulative flows, respectively, as

where the structural coefficients for the upper and lower flows, respectively, are

structural parameters



where the structural coefficients are

Here, structural parameters of energy pulsations



Since the velocity components have a unique presentation both for the vector and scalar descriptions of the kinematic and dynamic potentials, the kinetic energies also have a single description.
Substitution of the dual formula (109) for the Bernoulli potential be into the Bernoulli Equation (11) in the vector description returns the same expression for the dynamic pressure as the Bernoulli Equation in the scalar description (107)

Thus, the kinetic energies, the dynamic pressures, and the total pressures have a unique presentation both in the vector and scalar descriptions.
Substitution of the dynamic pressure in the hydrostatic Equation (5) yields the total pressure for the upper and lower cumulative flows, respectively,

where structural coefficients are given by (106) and (123).
When


When


In (127)-(128),




7. Decomposition of Harmonic Variables in the SKEF Structural Basis
Similar to two independent SKEF structures in two dimensions [5] , there are four independent SKEF structures in three dimensions

where


Thus, the family of four differentially independent SKEF structures

Computing the Laplacians of (129) by (130) and identities (43) shows that the SKEF structural basis


By (130), dot products of gradients to local isosurfaces




Thus, there are three couples of symmetric isosurfaces with the same absolute values of the scalar products of gradients. In two dimensions, the non-orthogonal isosurfaces are reduced to orthogonal isolines [5] .
For velocity components (44), the non-orthogonal harmonic SKEF structural basis is

where



Since


Taking the temporal derivatives of (44) by (93) and reducing to the SKEF structures using (47) give

where structural coefficients are



Decompositions of the temporal derivatives of the velocity components in the SKEF structural basis


For kinematic potentials (79) and dynamic potentials (97) and (105), the non-orthogonal harmonic SKEF structural basis is



Computation of elements of the SKEF structural basis


Decomposition of the dynamic potentials in the SKEF structural basis (133), (141) gives for the upper and lower flows, respectively,

Computation of elements of the SKEF structural basis by (140) and substitution in (144) returns local relationships between the dynamic potentials and the temporal derivatives of the velocity components

Since the SKEF structural basis is harmonic, there are 11 pairs of local and global functions










8. Experimental and Theoretical Verification by the System of Navier-Stokes PDEs
The classical proofs of existence theorems for series solutions of PDEs, see existence theorems of [3] and references therein, include three following steps: 1) to derive formal solutions, 2) to show that PDEs are satisfied, and 3) to find conditions of convergence. For the structural solutions of this paper, the first step is implemented in Sections 2-7, the second step is the point of this section, and the third step is not required since the structural solutions are exact and decompositions in the invariant structures are truncated.
The Navier-Stokes PDEs (1) in the scalar notation become



Theoretical computation of the directional derivatives of (146)-(148) by (120), (94)-(96), and (117)-(118) as a superposition of three products of the SKEF structures, which is reduced to the SDEF structure, yields for the upper and lower cumulative flows, respectively,



where the structural coefficients for Equation (149) are

for Equation (150) are

and for Equation (151) are

In the vector description, the pressure force of (146)-(148) is reduced by (5) and (125) to

Theoretical computation of the SKEF structures for the spatial derivatives of the Bernoulli potential (105)- (106) by (94)-(96) and comparison with the SKEF structures for the temporal derivatives of the velocity components (136)-(139) yields that these structures are related by

in agreement with decompositions in the SKEF structural basis of Section 7.
Taking theoretically the spatial derivative of the SDEF structure (117) in the x-direction gives for the upper and lower cumulative flows, respectively,

where the structural coefficients are

Similarly, the spatial derivative of the SDEF structure (117) with respect to y becomes

where the structural coefficients are

Finally, theoretical computation of the spatial derivative of the SDEF structure (117) in the z-direction returns for the upper and lower cumulative flows, respectively,

where the structural coefficients are

Thus, Equations (157)-(162) and (93)-(96) prove that the SDEF and SKEF structures are invariant with respect to spatial and temporal differentiation.
Application of (157)-(162) to the SDEF structure for the kinetic energy (122)-(123) and comparison with the SDEF structures for the directional derivatives of the velocity components (149)-(154) yields that these structures, similar to the SKEF structures in Section 7, are connected by

Substitution of (135), (155), (156), and (163) in Equations (146)-(148) shows that the Navier-Stokes PDEs are satisfied exactly by the structural solutions in the SKEF, SDEF, and polynomial structures both for the upper and lower cumulative flows. Similarly, computation of the spatial derivatives of the SKEF structures (120) for the velocity components by (94)-(96) and substitution in the continuity PDE (17) also reduces it to identity for the upper and lower cumulative flows.
The main results of this paper are summarized in the following theorem.
Existence Theorem. In the



defined by (112) and 25 constant structural coefficients
and the polynomial structures, there are upper and lower exact solutions for the velocity components









The structural solutions were computed through the theoretical programming with symbolic general terms, symbolic indices, and code-generated names of structural variables for a symbolic number of internal waves N in the virtual environment of the global variable Eqt by 33 developed procedures of 1938 code lines. Primarily, the exact solutions for the upper and lower cumulative flows with were discovered through the experimental programming for N = 3 and then verified by the system of the Navier-Stokes PDEs. Secondly, the cumulative solutions for the velocity components (44), the kinematic potentials (78)-(81), the dynamic potentials (97)-(100), (105)-106), the product of the SKEF structures (117)-(118), the total pressure (126), (106), (123), the temporal derivatives of the velocity components (136)-(139), the directional derivatives of the velocity components (149)-(154), the spatial derivatives of the Bernoulli potential (156), and the spatial derivatives (157)-(162) of the kinetic energy (122)-(123) of the upper and lower cumulative flows were derived through the theoretical programming and justified by the correspondent experimental solutions for N = 1, 3, 10. Finally, the theoretical solutions for the general terms of the spatial (94)-(96), temporal (136)-(139) and directional derivatives (149)-(154) of the velocity components (120)-(121), the spatial derivatives of the Bernoulli potential (105)-(106), and the spatial derivatives (157)-(162) of the kinetic energy (122)-(123) were verified by the system of the Navier- Stokes PDEs.
9. Discussion and Visualization
The structural solutions for conservative interaction of N internal waves in the upper and lower domains model generation, propagation, and interaction of internal waves in the atmosphere and ocean. For fluid-dynamic engineering, existence of these exact solutions of the Navier-Stokes PDEs means existence of an enormous source of the kinetic energy of the internal waves beneath the ocean surface. This source of energy is continuously maintained by perpetual surface waves and it is not affected by viscous dissipation since the velocity field is harmonic.
The exact structural solutions are neutrally stable with respect to any number M of wave perturbations in the class of SKEF structures since the resulting flows are reduced to the upper and lower cumulative flows with N + M internal waves. Since the upper and lower cumulative flows are harmonic, the structural solutions do not depend on the Reynolds number, similar to how all solutions for conservative systems do not depend on dissipation parameters. For the same reason, initial conditions are not required for conservative PDEs, which produce solutions propagating for all times. In conservative solutions, any moment may be treated as an initial moment.
The implemented experimental and theoretical programming methods represent an indispensable Computational Mathematics (COMP MATH) tool, without which discovery and proof of the structural solutions would be impossible since the artificial intelligence of the Maple theoretical computation programs far exceeds the human intelligence. For instance, a calculation of the directional derivative of a single scalar variable u, which produces Equations (149) and (152) for the upper cumulative flow, requires 100 substitutions for 100 structural coefficients with the code-generated names:

The listed names of computational variables in fact are words of a new computational language, which is required to compute theoretically exact formulas for the new COMP MATH data structures: the SKEF and SDEF structures, while this COMP MATH language is developed in the process of computation by the Maple program itself.
The structural solutions in the SKEF structures for the velocity components (120)-(121), the kinematic potentials (78)-(81), and the dynamic potentials (97)-(100), in the SDEF structures for the kinetic energy (122)-(123), in the SKEF-SDEF structures for the dynamic pressure (125), and in the SKEF-SDEF and polynomial structures for the total pressure (126), (106), (123) depend on 14N independent parameters








periods. When





The SKEF structures of the lower cumulative flow are visualized for the scalar potential








Figure 2. Kinematic potentials of the lower cumulative flow: (a)
























The SDEF structures are shown for the kinetic energy






10. Conclusions
For the Navier-Stokes system of PDEs in three dimensions, the global existence theorem for periodic solutions vanishing at infinity of the upper and lower domains is proved by the


Figure 3. Kinetic energy (a) and dynamic pressure (b) of the lower cumulative flow.
tions. Invariance of the SKEF and SDEF structures with respect to differentiation is shown. The nonlinear algebra of the SKEF structures is developed. The non-orthogonal SKEF structural basis for harmonic functions is constructed and decompositions of the fluid-dynamic variables in this basis are obtained. The conservative system of N internal waves is neutrally stable with respect to M wave perturbations, and it is not affected by viscous dissipation.
The computational method of decomposition in invariant structures continues the analytical methods of separation of variables, undetermined coefficients, and series expansions [3] [5] [10] -[12] . In the current paper, the method of decomposition in invariant structures is extended into three dimensions. By this method, the vorticity and continuity PDEs are reduced to 12 homogeneous ODEs of first order and four linear AEs, the Helmholtz PDEs to 12 inhomogeneous ODEs of first order and 16 linear AEs, the Lamb-Helmholtz PDEs to four inhomogeneous ODEs of first order and eight linear AEs, and the Bernoulli equation is reduced to a linear equation in the SKEF and SDEF structures both for the upper and lower flows. To summarize, the system of four Navier- Stokes PDEs is reduced to the linear system of 57 equations, including 28 ODEs and 29 AEs.
Experimental discovery and theoretical proof of the exact solutions are implemented through experimental programming in Maple™ with lists of equations and expressions for numerical indices and numeric N = 3 by 33 developed procedures of 1748 code lines and theoretical programming with symbolic general terms, symbolic indices, and code-generated names of structural variables for symbolic N by 33 developed procedures of 1938 code lines. The developed procedures allow for theoretical derivations in the environment of novel COMP MATH data structures—the SKEF, SDEF, and SKEF-SDEF structures that are extended in this paper into three dimensions.
Acknowledgements
The author thanks I. Tari and S. P. Bhavaraju for the stimulating discussion at the 2013 SIAM Annual Meeting. Support of the College of Mount Saint Vincent and CAAM is gratefully acknowledged.
References
- Lamb, S.H. (1945) Hydrodynamics. 6th Edition, Dover Publications, New York.
- Pozrikidis, C. (2011) Introduction to Theoretical and Computational Fluid Dynamics. 2nd Edition, Oxford University Press, Oxford.
- Miroshnikov, V.A. (2005) The Boussinesq-Rayleigh Series for Two-Dimensional Flows Away from Boundaries. Applied Mathematics Research Express, 2005, 183-227. http://dx.doi.org/10.1155/amrx.2005.183
- Korn, G.A. and Korn, T.A. (2000) Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. 2nd Revised Edition, Dover Publications, New York.
- Miroshnikov, V.A. (2014) Nonlinear Interaction of N Conservative Waves in Two Dimensions. American Journal of Computational Mathematics, 4, 127-142. http://dx.doi.org/10.4236/ajcm.2014.43012
- Miroshnikov, V.A. (1995) Solitary Wave on the Surface of a Shear Stream in Crossed Electric and Magnetic Fields: The Formation of a Single Vortex. Magnetohydrodynamics, 31, 149-165. http://mhd.sal.lv/contents/1995/2/MG.31.2.5.R.html
- Miroshnikov, V.A. (1996) The Finite-Amplitude Solitary Wave on a Stream with Linear Vorticity. European Journal of Mechanics, B/Fluids, 15, 395-411.
- Miroshnikov, V.A. (2002) The Boussinesq-Rayleigh Approximation for Rotational Solitary Waves on Shallow Water with Uniform Vorticity. Journal of Fluid Mechanics, 456, 1-32. http://dx.doi.org/10.1017/S0022112001007352
- Kochin, N.E., Kibel, I.A. and Roze, N.V. (1964) Theoretical Hydromechanics. John Wiley & Sons Ltd., Chichester.
- Miroshnikov, V.A. (2009) Spatiotemporal Cascades of Exposed and Hidden Perturbations of the Couette Flow. Advances and Applications in Fluid Dynamics, 6, 141-165. http://www.pphmj.com/abstract/4402.htm
- Miroshnikov, V.A. (2012) Dual Perturbations of the Poiseuille-Hagen Flow in Invariant Elliptic Structures. Advances and Applications in Fluid Dynamics, 11, 1-58. http://www.pphmj.com/abstract/6711.htm
- Miroshnikov, V.A. (2014) Interaction of Two Pulsatory Waves of the Korteweg-de Vries Equation in a Zigzag Hyperbolic Structure. American Journal of Computational Mathematics, 4, 254-270. http://dx.doi.org/10.4236/ajcm.2014.43022




















































































