American Journal of Computational Mathematics
Vol.3 No.4(2013), Article ID:40961,11 pages DOI:10.4236/ajcm.2013.34042
The Correlation and Linear Regression Analysis between Annual GDP Growth Rate and Money Laundering in Albania during the Period 2007-2011*
1University “Pavaresia” in Vlora, Vlora, Albania
2University of New York in Tirana, Tirana, Albania
Email: #llambrini_kristi@yahoo.com
Copyright © 2013 Llambrini Sota, Fejzi Kolaneci. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 5, 2013; revised September 12, 2013; accepted September 18, 2013
Keywords: Illicit Money; Money Laundering; GDP Growth Rate; Linear Regression; Pearson’s Coefficient of Correlation
ABSTRACT
This study is the first attempt to investigate the relationship between the annual GDP growth rate and money laundering in the Republic of Albania during the period 2007-2011. The main result of the study: there is a negative correlation between money laundering process and economic growth rate in Albania during the specified period; there is a negative correlation between money laundering and import, but there is a positive correlation between money laundering and the government expenditure, as well a positive correlation between money laundering and export. More concretely: 1) The coefficient of correlation between cases referred in the prosecutor’s office for money laundering (X) and the annual GDP growth rate (Y) is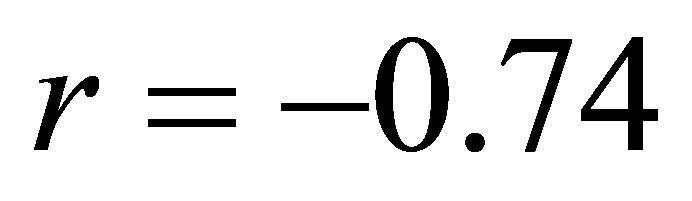 . The equation of the linear regression is
. The equation of the linear regression is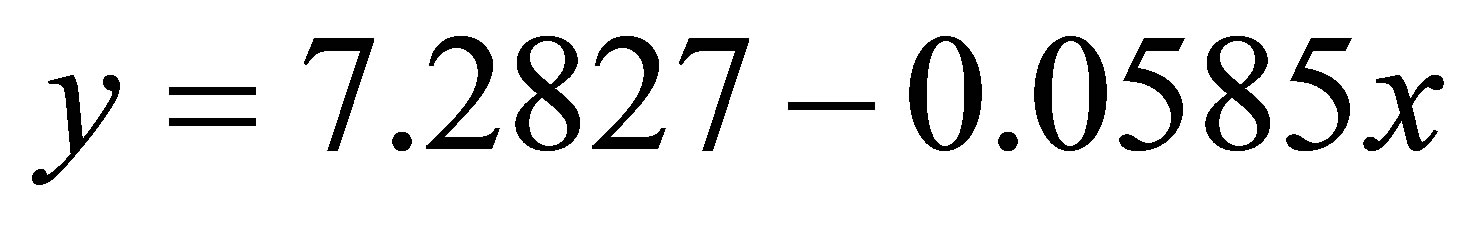 . 2) The coefficient of correlation between cases reported in the police for money laundering (X) and the annual GDP growth rate (Y) is
. 2) The coefficient of correlation between cases reported in the police for money laundering (X) and the annual GDP growth rate (Y) is , while the equation of the linear regression is
, while the equation of the linear regression is . 3) The coefficient of correlation between reported CAA (Cases for Alleged Activity) for money laundering (X) and the annual GDP growth rate (Y) is
. 3) The coefficient of correlation between reported CAA (Cases for Alleged Activity) for money laundering (X) and the annual GDP growth rate (Y) is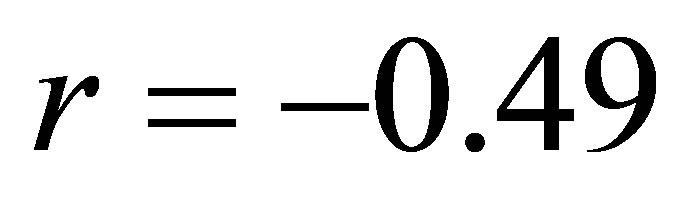 , while the equation of the linear regression is
, while the equation of the linear regression is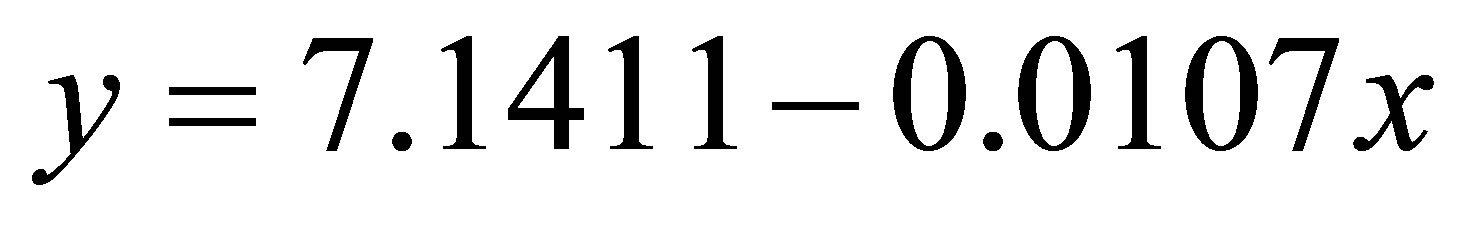 . 4) The coefficient of correlation between government expenditures and the cases referred in the prosecutor’s office for money laundering is
. 4) The coefficient of correlation between government expenditures and the cases referred in the prosecutor’s office for money laundering is . 5) The coefficient of correlation between government expenditures and the cases reported in the police for money laundering is
. 5) The coefficient of correlation between government expenditures and the cases reported in the police for money laundering is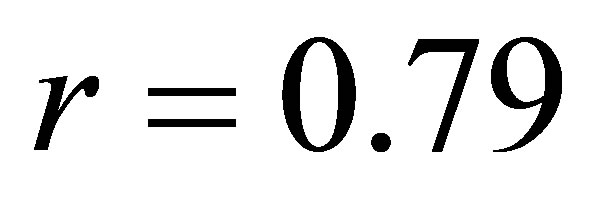 . 6) The coefficient of correlation between net export and the cases referred in the prosecutor’s office for money laundering is
. 6) The coefficient of correlation between net export and the cases referred in the prosecutor’s office for money laundering is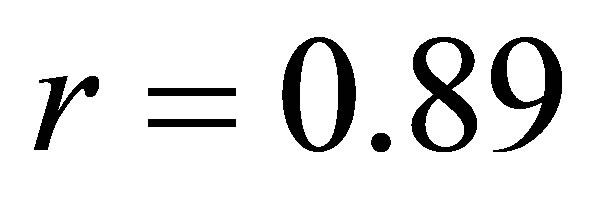 . 7) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and unemployment rate is
. 7) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and unemployment rate is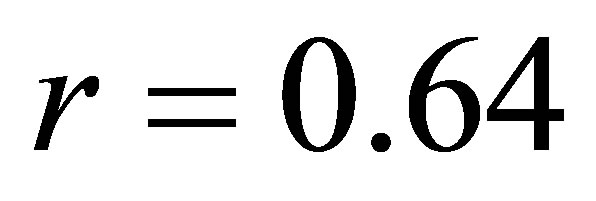 . 8) The coefficient of correlation between the cases reported in the police for money laundering and unemployment rate is
. 8) The coefficient of correlation between the cases reported in the police for money laundering and unemployment rate is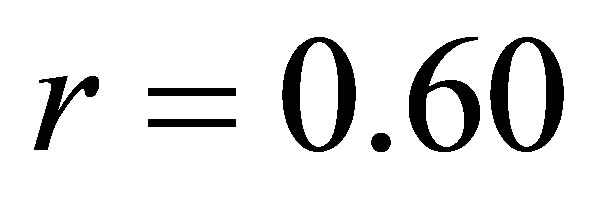 . 9) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and inflation rate is
. 9) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and inflation rate is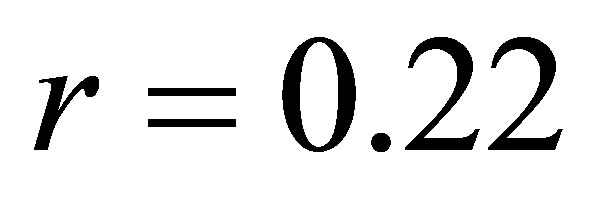 . 10) The coefficient of correlation between the cases reported in the police for money laundering and inflation rate is
. 10) The coefficient of correlation between the cases reported in the police for money laundering and inflation rate is . 11) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and the investments in Albania is
. 11) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and the investments in Albania is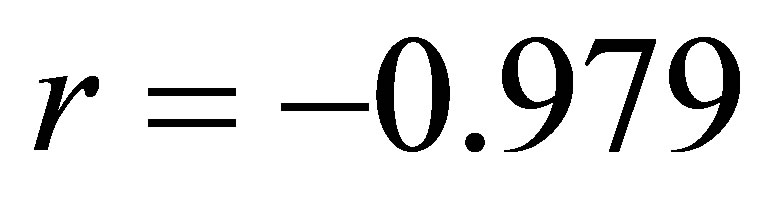 . 12) The coefficient of correlation between the cases reported in the police for money laundering and inflation rate is
. 12) The coefficient of correlation between the cases reported in the police for money laundering and inflation rate is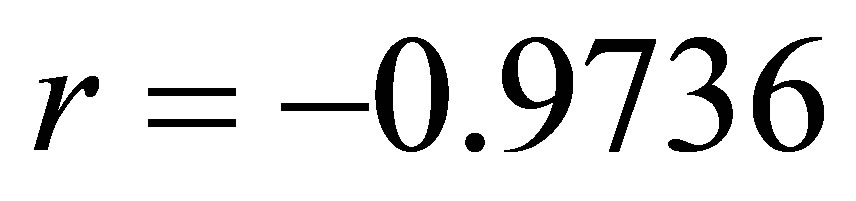 . 13) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and the foreign direct investments in Albania is
. 13) The coefficient of correlation between the cases referred in the prosecutor’s office for money laundering and the foreign direct investments in Albania is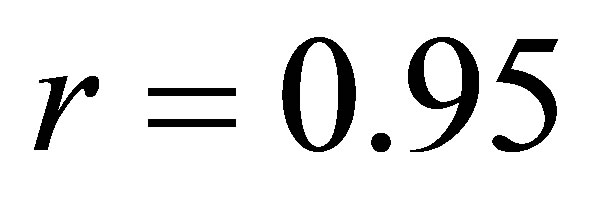 . 14) The coefficient of correlation between the cases reported in the police for money laundering and the foreign direct investments in Albania is
. 14) The coefficient of correlation between the cases reported in the police for money laundering and the foreign direct investments in Albania is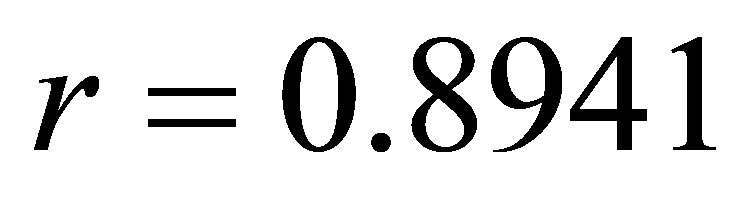 .
.
1. Introduction
Nowadays one of the major issues in the world is antimoney laundering. According to the IMF (International Monetary Funds), money laundering has become one of the most serious activities faced by the international financial community [1]. It became harmful because of its necessary coexistence with crime. The value of global money laundering amounted to 2.5 trillion USD (see [2]). However, in 2011, it is estimated to be over 3.0 trillion USD. But before going further, it is necessary to clarify some of the concepts that will be used in this paper.
Definition 1. Illicit money refers to the money that is originated from illicit activities, especially from the criminal ones [2].
Definition 2. Money laundering is the process of obscuring the source, ownership or use of funds, usually cash, that are profits of illicit activity [3].
In other words, money laundering is the process of creating the appearance that large amounts of money obtained from serious crimes, such as drug trafficking, human trafficking, weapons trafficking, corruption, counterfeiting of currency, or terrorist activity, originated from legitimate source (see [1,2]).
Definition 3. Guilty of money laundering is that a person hides or disguises the true origin, the source, movement or alienation of money, for which he (she) has knowledge that directly or indirectly derives from illegal activities, especially criminal (see [2,3]).
Remark. This definition is according to the EU’s legislation, as well as UN’s legislation. Furthermore, it is also used by the World Bank and Interpol.
Definition 4. GDP (Gross Domestic Product) is the market value of all finished goods and services within a country during a given period of time. The GDP is given by the formula: Y = C + I + G + NX, where C denotes private consumption, I denotes gross investments, G denotes government spending and NX denotes Net Exports = Exports − Imports (see [1,4]).
According to some recent estimation, money laundering constitutes about 6% - 8% of GDP in USA, 7% - 9% of GDP in UK, Germany, France, Italy, etc. However, some scientists claim that the amount of official data is underestimated compared to the reality of money laundering process (see [2,3]). Actually, to fight money laundering in nations like America, where the relationship between the amount of money laundering and the annual GDP growth rate is positive, can be a double-edged sword. This happens because if illicit money is not turned into legal capital, they cannot be used into the economy, but only as a capital for illegal activities. While, in other countries of Europe such as France and Germany, the relationship between money laundering and GDP is negative (see [1,2,5]). Regarding the Republic of Albania there is not, yet, any study which analyses with a mathematical statistic method the relationship between money laundering and the annual GDP growth. Hence, our study is a first oriented toward this topic.
2. Mathematical Model
The linear regression analysis is used to estimate the impact that the process of money laundering has on the economic growth, in the case of Albania over the period January 2007-December 2011. The random variable X denotes the annual number of cases of money laundering, while the random variable Y denotes the corresponding rate of annual real GDP growth. X represents the explanatory variable (input). Y represents the dependent variable (output). The sources of the data are INSTAT (Albanian Institute of Statistics), Bank of Albania (BoA), see [6-8] and General Directory for the Prevention of Money Laundering, Albanian Financial Intelligence Unit, AFIU 2011, see [9]. The Table 1 contains the data sets for the random variables X and Y.
3. Main Results
Coefficient of correlation r = −0.74 Coefficient of determination d = 0.55 Linear regression equation y = 7.2827 – 0.0585x
In Figure 1 using the linear correlation and regression analysis, as well as the given data set, we obtain the following results:
The coefficient of correlation between cases referred in the prosecutor’s office for money laundering and the annual GDP growth rate is r = −0.74, which (according to Gelfand’s classification) indicates a moderate negative correlation between the two random variables. The coefficient of determination is d = r2 = 55%, which implies that 55% of the total variation in annual GDP growth rate can be explained by the variation in the number of cases of money laundering, while 45% of the total variation in GDP growth rate must be explained by the impact of other factors. The linear regression equation is y = 7.2827 − 0.0585x, where x denotes the number of cases referred in prosecutor’s office for money laundering and y denotes the annual GDP growth rate for Albania during the period of January 2007-December 2011.
Coefficient of correlation r = −0.81 Coefficient of determination d = 0.66 Linear regression equation y = 7.3223 − 0.0249x
In Figure 2 we have used the correlation analysis to measure the strength of the relationship between the cases referred in police for money laundry and annual GDP
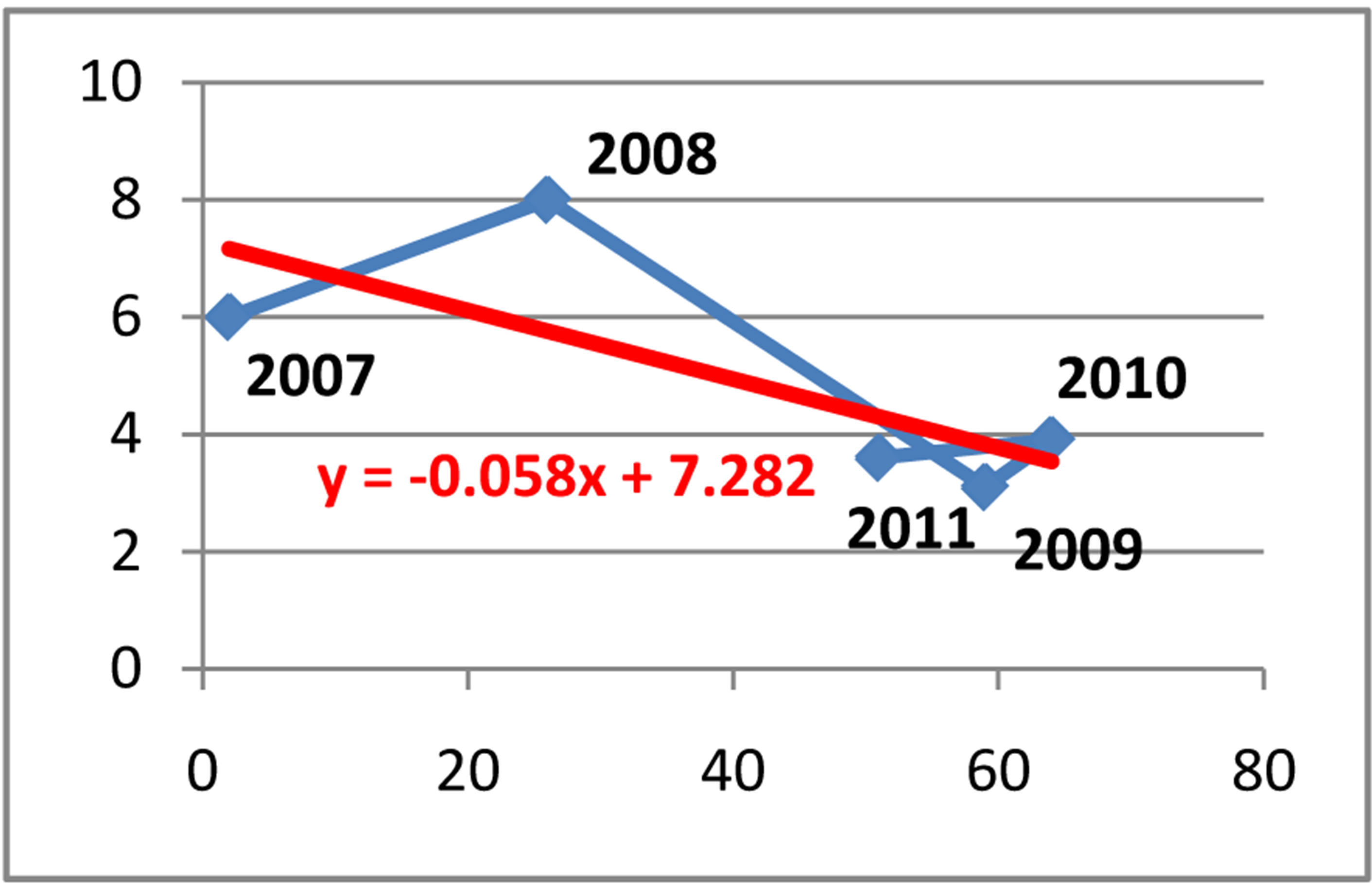
Figure 1. Relationship between the cases referred in the prosecutor’s office for money laundering and the annual GDP growth rate during 2007-2011.
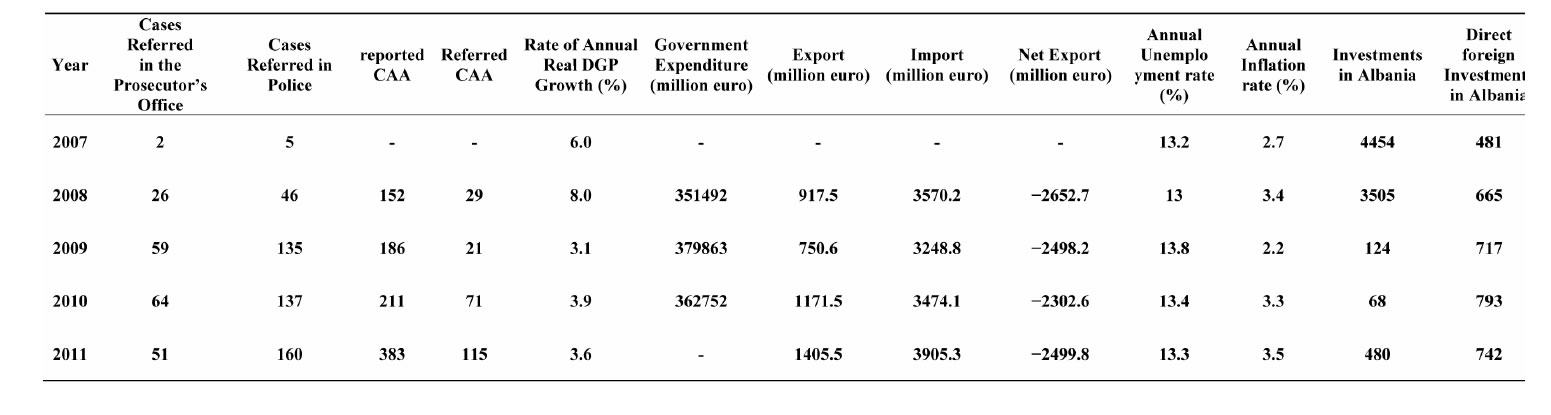
Table 1.Annual number of cases of money laundering and rate of annual real GDP growth or its components.
The pearson’s coefficient of correlation is r = −0.81, which (according to Gelfand’s classification) indicates a strong negative correlation between the two random variables. The coefficient of determination is d = r2 = 66%. This result can be interpreted in this way: 66% of the total variation in GDP growth rate can be explained by the variation in the number of cases referred in police for money laundering. But, 34% of the total variation in GDP growth rate must be explained by the impact of other factors.
The linear regression equation is y = 7.27 − 0.024x, where x denotes the number of cases referred in police for money laundry, and y denotes the annual GDP growth rate for Albania during the period January 2007- December 2011.
Coefficient of correlation r = −0.49 Coefficient of determination d = 0.24 Linear regression equation y = 7.1411 − 0.0107x
In Figure 3 the coefficient of correlation r = −0.49 indicates a moderate negative correlation between the two random variables. While, the coefficient of determination d = r2 = 24%. This means that 24% of the total variation in GDP growth rate is explained by the variation of reported CAA (Cases for Alleged Activity), whereas the other 66% is explained by the other factors.
The equation for the linear regression analysis is y = 7.1411 − 0.0107x, where x denotes the reported CAA and y denotes the annual GDP growth rate for Albania
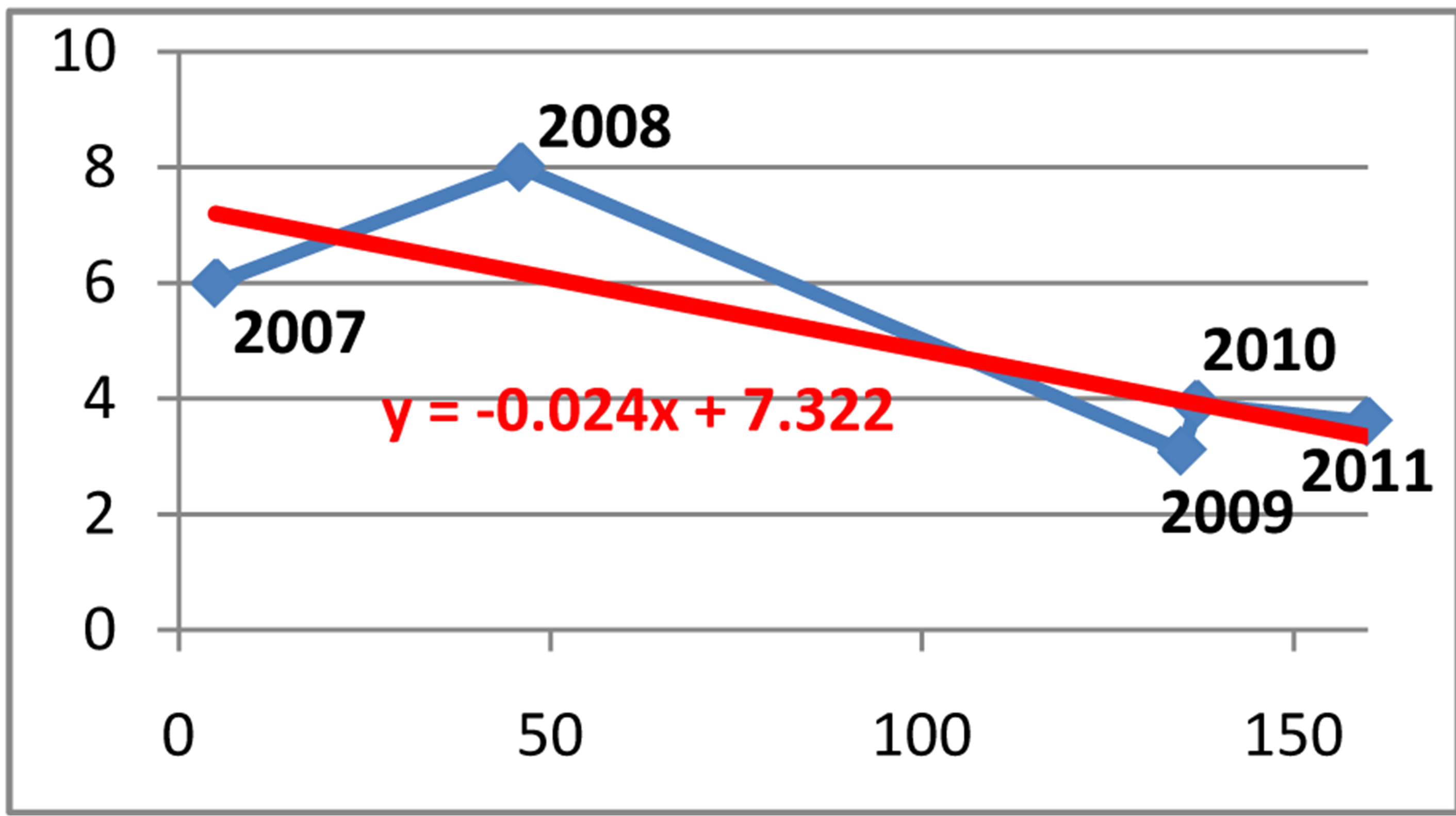
Figure 2. Relationship between the cases reported in the police for money laundering and the annual GDP growth rate during 2007-2011.
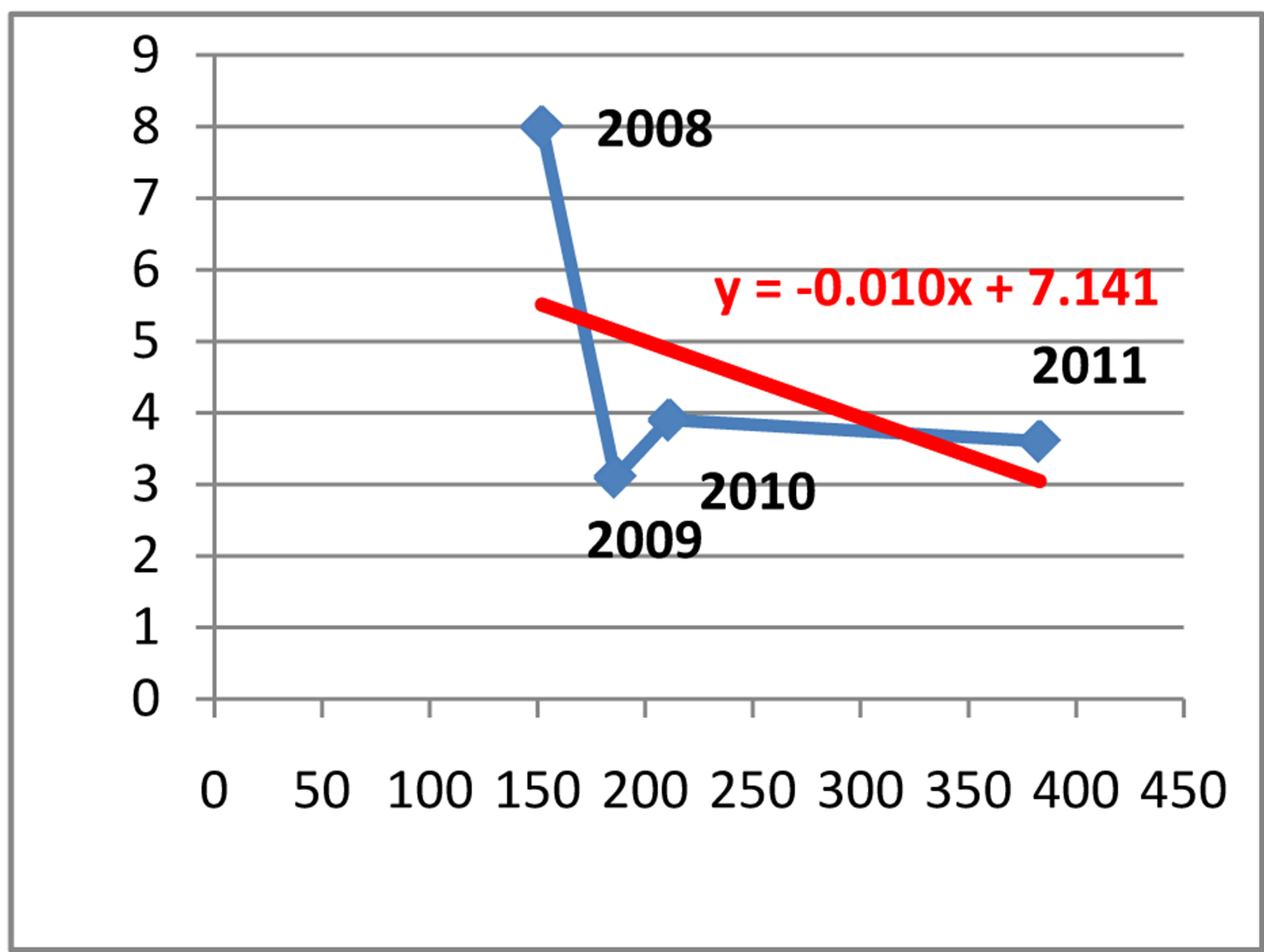
Figure 3. Relationship between reported CAA and the annual GDP growth during 2008-2011.
growth rate.
during the period January 2008- December 2011.
Coefficient of correlation r = −0.36
Coefficient of determination d = 0.13%
Linear regression equation y = 5.7977 − 0.0195xIn Figure 4 using the linear correlation and the regression analysis we have obtained that there is a relationship between the CAA (Cases for Alleged Activity) referred for money laundry and the annual GDP growth rate.
The coefficient of correlation is r = −0.36, which indicates a moderate negative correlation between the two random variables. While the coefficient of determination is d = r2 = 13%.
We can interpret this result in this way: 13% of the total variation in GDP growth rate can be explained by the variation in the referred CAA for money laundering. But 87% of the total variation in GDP growth rate must be explained by the impact of other factors.
The linear regression equation is y = 5.7977 − 0.0195x, where x denotes the number of referred CAA, and y denotes the annual GDP growth rate for Albania during the period January 2008-December 2011.
Coefficient of correlation r = 0.72
Coefficient of determination d = 0.52
Equation of linear regression y = 339877 + 499.83x
Coefficient of correlation r = 0.79
Coefficient of determination d = 0.62
Equation of linear regression y = 341708 + 216.92x
Using the regression and correlation analysis we have concluded that there is a relationship between government spending and cases referred prosecutor’s office and reported in the police for money laundering.
In Figure 5 the coefficient of correlation is correspondingly r = 0.72, which indicate a strong positive correlation between the variables. While, the coefficient of determination is respectively d = r2 = 52% (or d = 62%). This result is interpreted in this way: 52% (or 62%) of the total government spending can be explain by the cases referred in the prosecutor’s office (or the ones reported
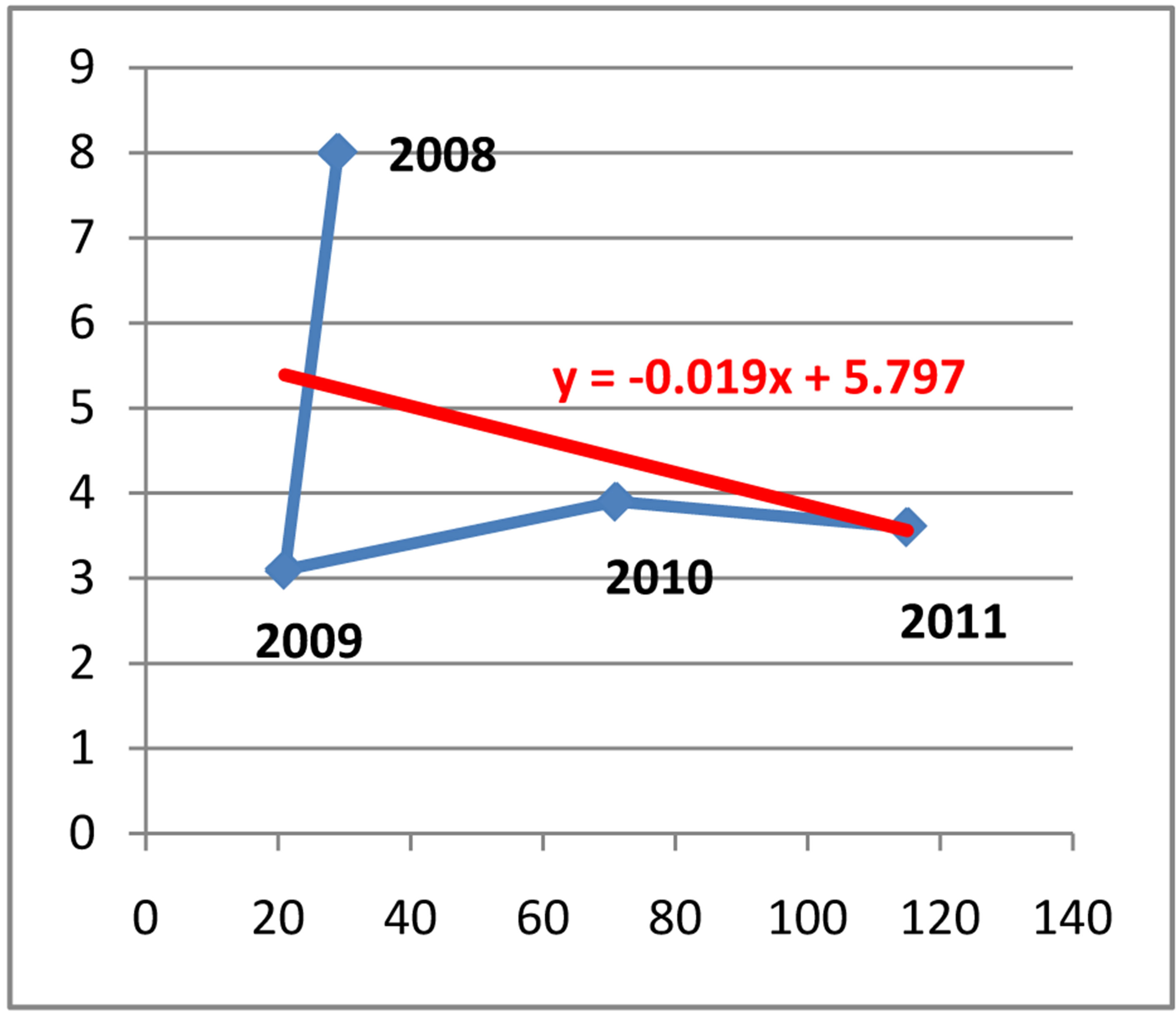
Figure 4. Relation between referred CAA and the annual GDP growth rate during 2008-2011.
in the police) for money laundering. But, 48% (or 38%) of the total government spending is explain by other factors.
The equation of the linear regression for the cases referred in the prosecutor`s office is y = 339877 + 499.83x, where x denotes the cases referred in prosecutor’s office, and y denotes the government spending in the Republic of Albania during the period of time January 2008-December 2010.
In Figure 6 the equation of the linear regression for the cases reported in the police is y = 341708 + 216.92x, where x denotes the cases reported in the police, and y denotes the government spending in the Republic of Albania during the period of time January 2008-December 2010.
Coefficient of correlation r = 0.17
Coefficient of determination d = 0.03
Equation of linear regression y = 912.45 + 2.9765x
Coefficient of correlation r = 0.50
Coefficient of determination d = 0.25
Equation of linear regression y = 720.8 + 2.8491x
Using the linear regression and correlation analysis we have concluded that there is a relationship between export and cases referred in the prosecutor’s office and the ones reported in the police for money laundering.
The coefficient of correlation between cases referred in the prosecutor’s office and the export is r = 0.17, while between cases reported in the police and export is r = 0.50, which indicates, respectively, a weak and a moderate positive correlation between the variables. The

Figure 5. Relation between government spending and cases referred in prosecutor’s office during 2008-2010.
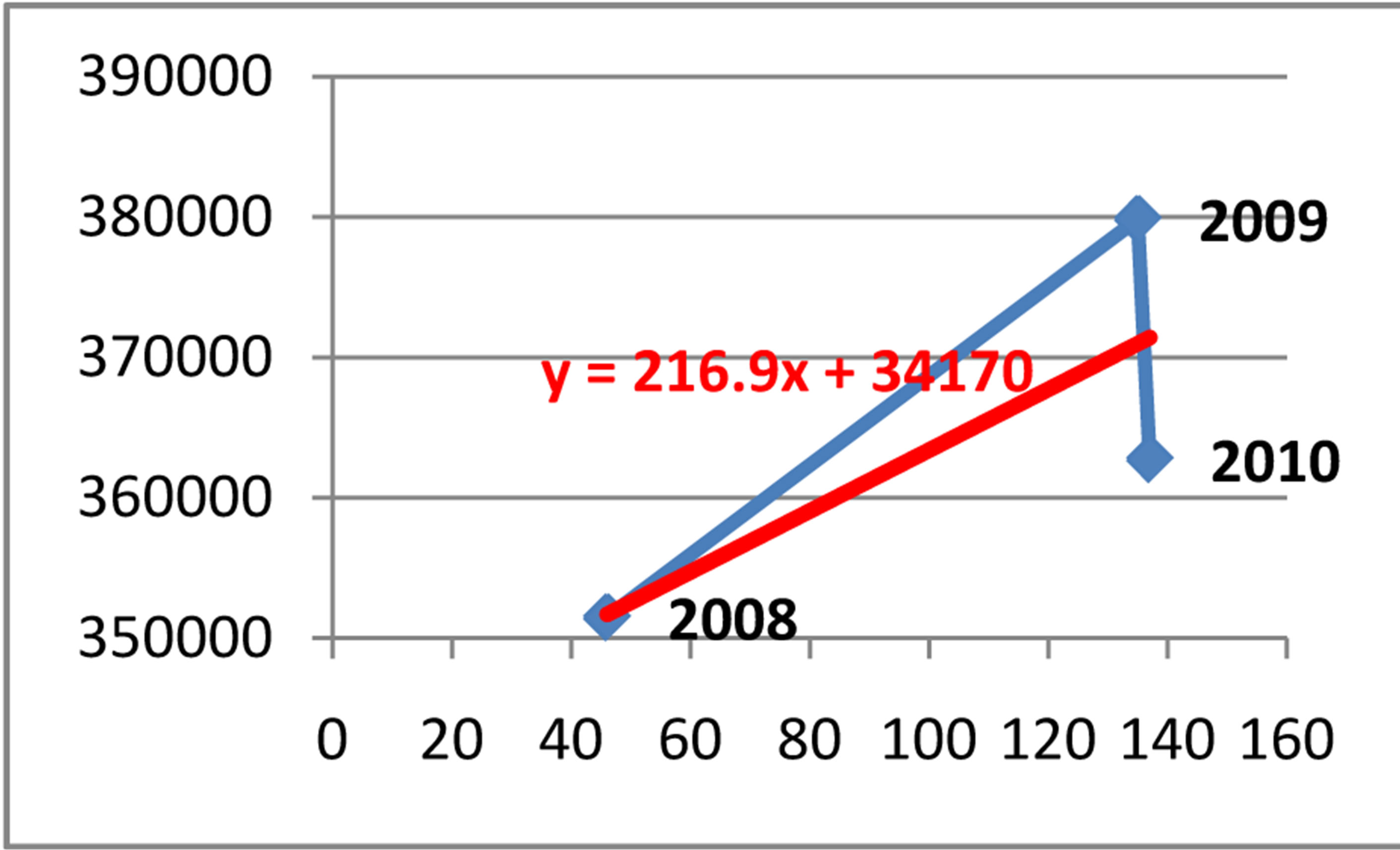
Figure 6. Relationship between government spending and cases referred in the police during 2008-2010.
coefficient of determination is respectively d = r2 = 3% or d = 25%. In Figure 7 the equation of the linear regression for the cases referred in the prosecutor’s office is y = 912.45 + 2.9765x, where x denotes the cases referred in the prosecutor’s office for money laundering, and y denotes the export in the Republic of Albania during the period of January 2008-December 2011. In Figure 8 the equation of the linear regression for the cases reported in the police for money laundering is y = 720.8 + 2.8491x, where x indicates the cases reported in the police, and y indicates the export during the period of January 2008-December 2011.
Coefficient of correlation r = −0.28
Coefficient of determination d = 0.08
Equation of linear regression y = 3778.1 − 4.5701x
Coefficient of correlation r = 0.17
Coefficient of determination d = 0.03
Equation of linear regression y = 3440.8 + 0.9103x
Using the linear regression and correlation analysis we have concluded that there is a relationship between import and cases referred in the prosecutor’s office, as well as the ones reported in the police for the money laundering.
The coefficient of correlation is respectively r = −0.28 (or r = 0.17), which indicates, correspondingly, a weak negative and positive correlation between the given values. The coefficient of determination is respectivelyd = r2 = 8% or d = 3%.
In Figure 9 the equation of the linear regression for the cases referred in the prosecutor’s office is y = 3778.1 − 4.5701x, where x denotes the cases referred in the
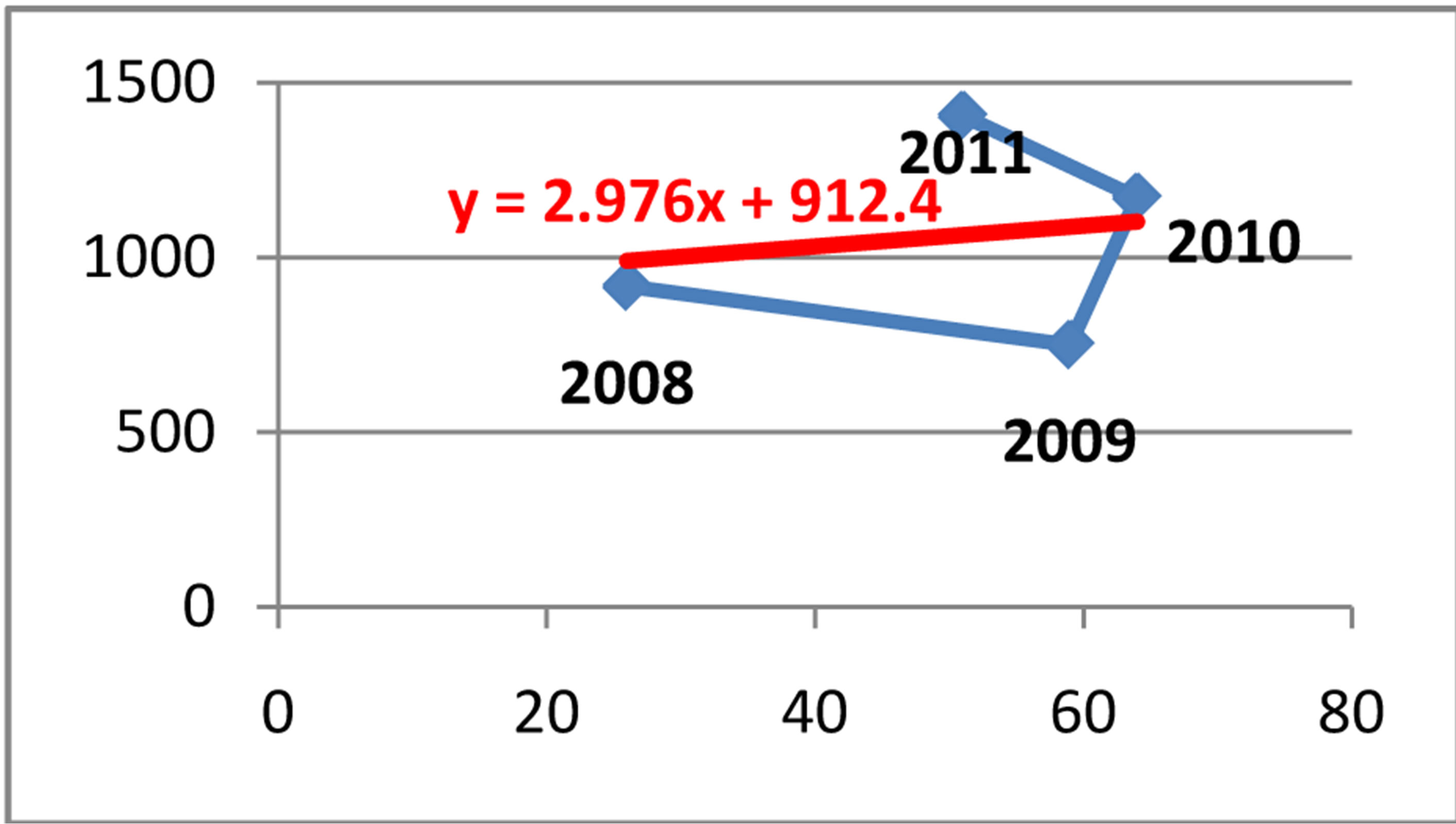
Figure 7. Relation between export and cases referred in prosecutor’s office for money laundering.
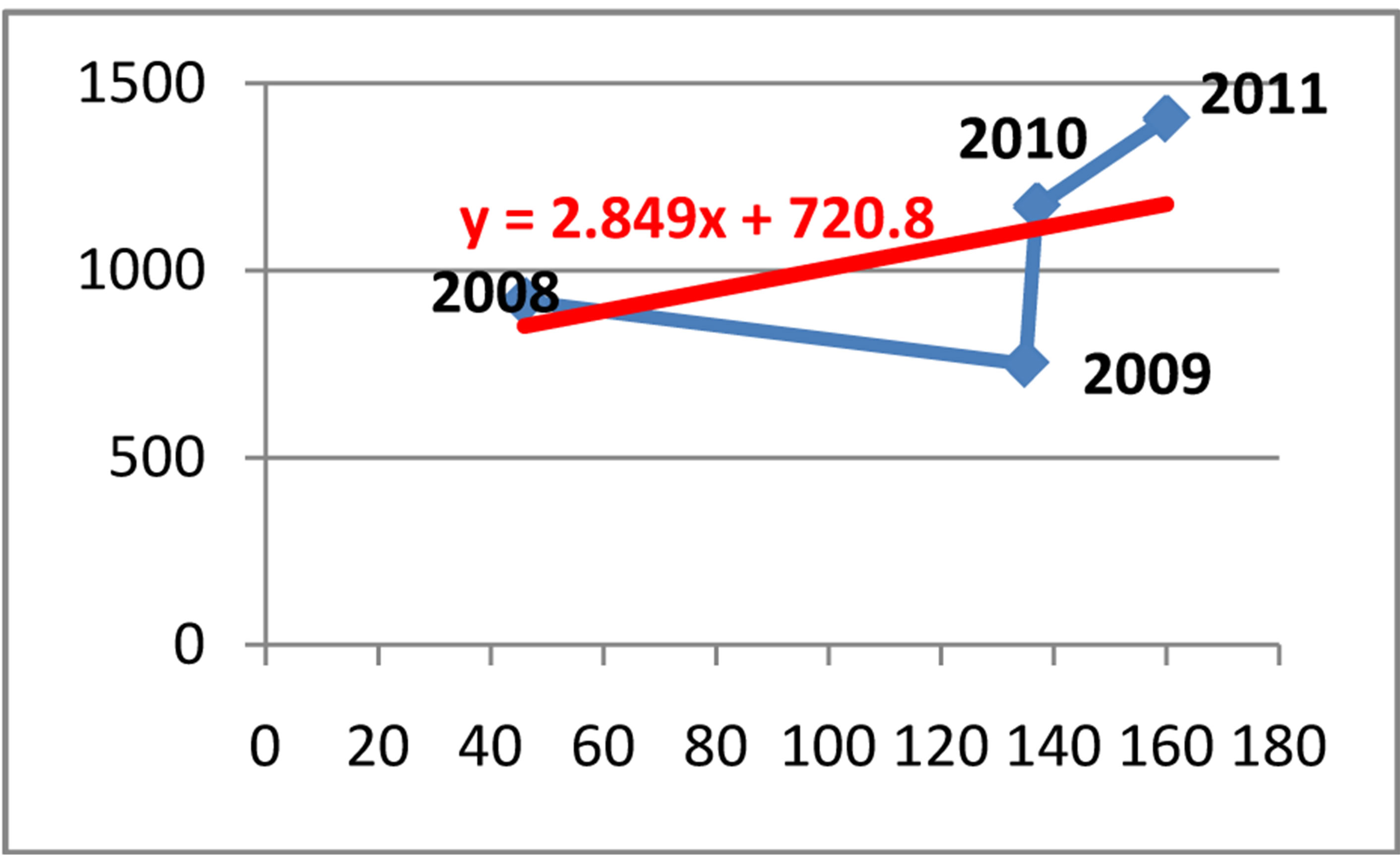
Figure 8. Relationship between export and cases reported in the police for money laundering during 2008-2011.
prosecutor’s office for money laundering, and y denotes the import in the Republic of Albania during the period of January 2008-December 2011. In Figure 10, the equation of the linear regression for the cases reported in the police for money laundering is y = 3440.8 + 0.9103x, where x indicates the cases reported in the police, and y indicates the import during the period of January 2008- December 2011.
Coefficient of correlation r = 0.89
Coefficient of determination d = 0.79
Equation of linear regression y = −2865.7 + 7.5466x
Coefficient of correlation r = 0.68
Coefficient of determination d = 0.46
Equation of linear regression y = −2720 + 1.9389x
Using the regression and correlation analysis we have concluded that there is a relationship between net export and cases referred in the prosecutor’s office and reported in the police for money laundering.
In Figure 11, the coefficient of correlation is correspondingly r = 0.89, which indicate a strong and moderate positive correlation between the variables. While, the coefficient of determination is respectively d = r2 = 79% (or d = 46%). This result is interpreted in this way: 79% (or 46%) of the total net export can be explained by the cases referred in prosecutor’s office (or the ones reported in the police) for money laundering. But, 21% (or 54%) of the total net export is explain by other factors.
The equation of the linear regression for the cases referred in the prosecutor’s office is y = −2865.7 + 7.5446x, where x denotes the cases referred in prosecutor’s office, and y denotes the net export in the Republic of Albania
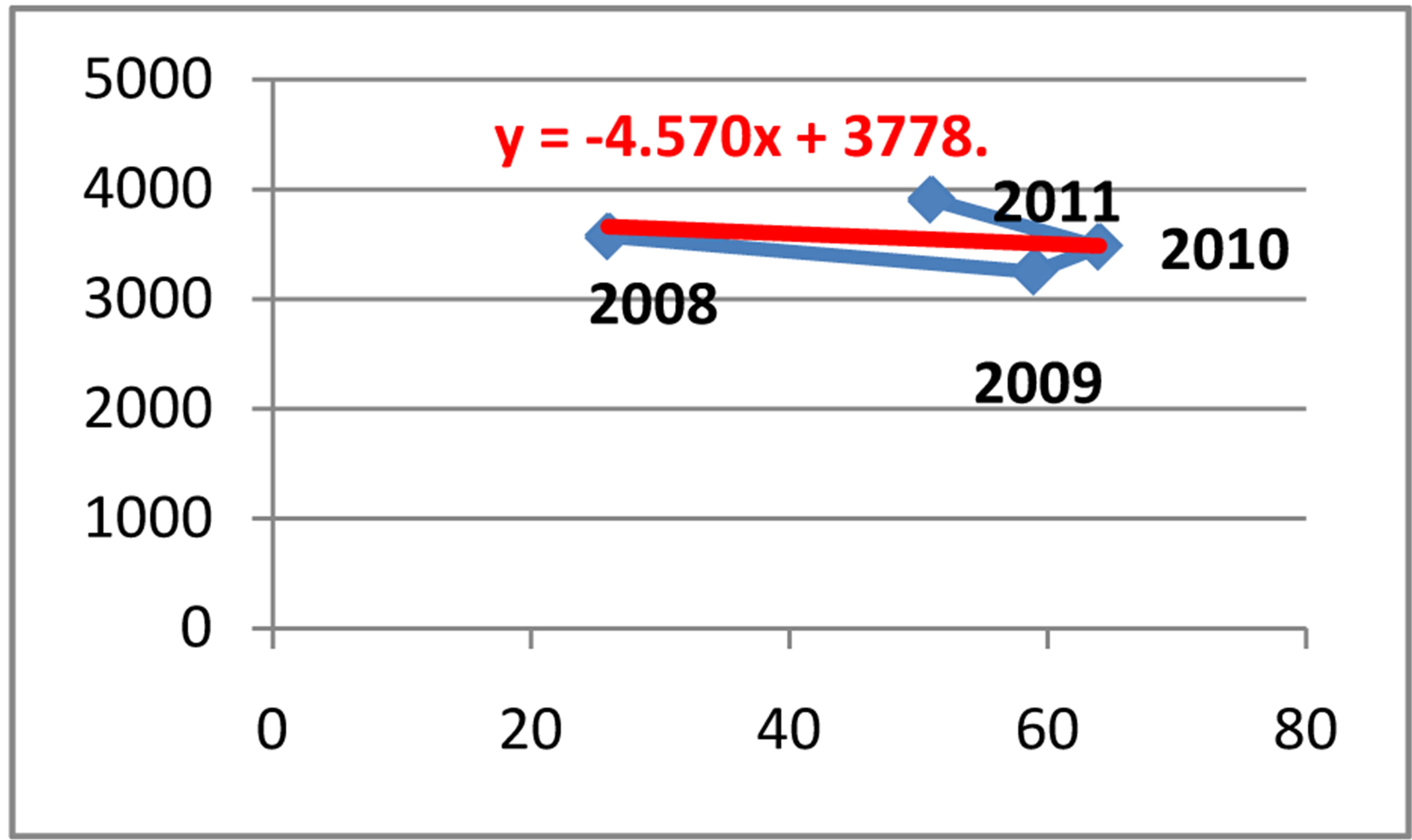
Figure 9. Relationship between import and cases referred in prosecutor’s office for money laundering.

Figure 10. Relationship between import and cases reported in the police for money laundering.
during the period of time January 2008-December 2011.
In Figure 12 the equation of the linear regression for the cases reported in the police is y = −2720 + 1.9389x, where x denotes the cases reported in the police, and y denotes the net export in the Republic of Albania during the period of time January 2008-December 2011.
Coefficient of correlation r = 0.22
Coefficient of determination d = 0.05
Equation of linear regression y = −2.9712 + 0.0012x
Coefficient of correlation r = 0.136
Coefficient of determination d = 0.02
Equation of linear regression y = −2.9113 + 0.0011x
Using the regression and correlation analysis we have concluded that there is a relationship between annual inflation rate and the cases referred in the prosecutor’s office and reported in the police for money laundering.
The coefficient of correlation is correspondingly r = 0.22 (or r = 0.136), which indicate a weak positive correlation between the variables. While, the coefficient of determination is respectivelyd = r2 = 5% (or d = 2%). This result is interpreted in this way: 5% (or 2%) of the total net export can be explained by the cases referred in prosecutor’s office (or the ones reported in the police) for money laundering. But, 95% (or 98%) of the total net export is explain by other factors.
In Figure 13 the equation of the linear regression for the cases referred in the prosecutor’s office is y = −2.9712 + 0.0012x , where x denotes the cases referred in prosecutor’s office, and y denotes the net export in the Republic of Albania during the period of time
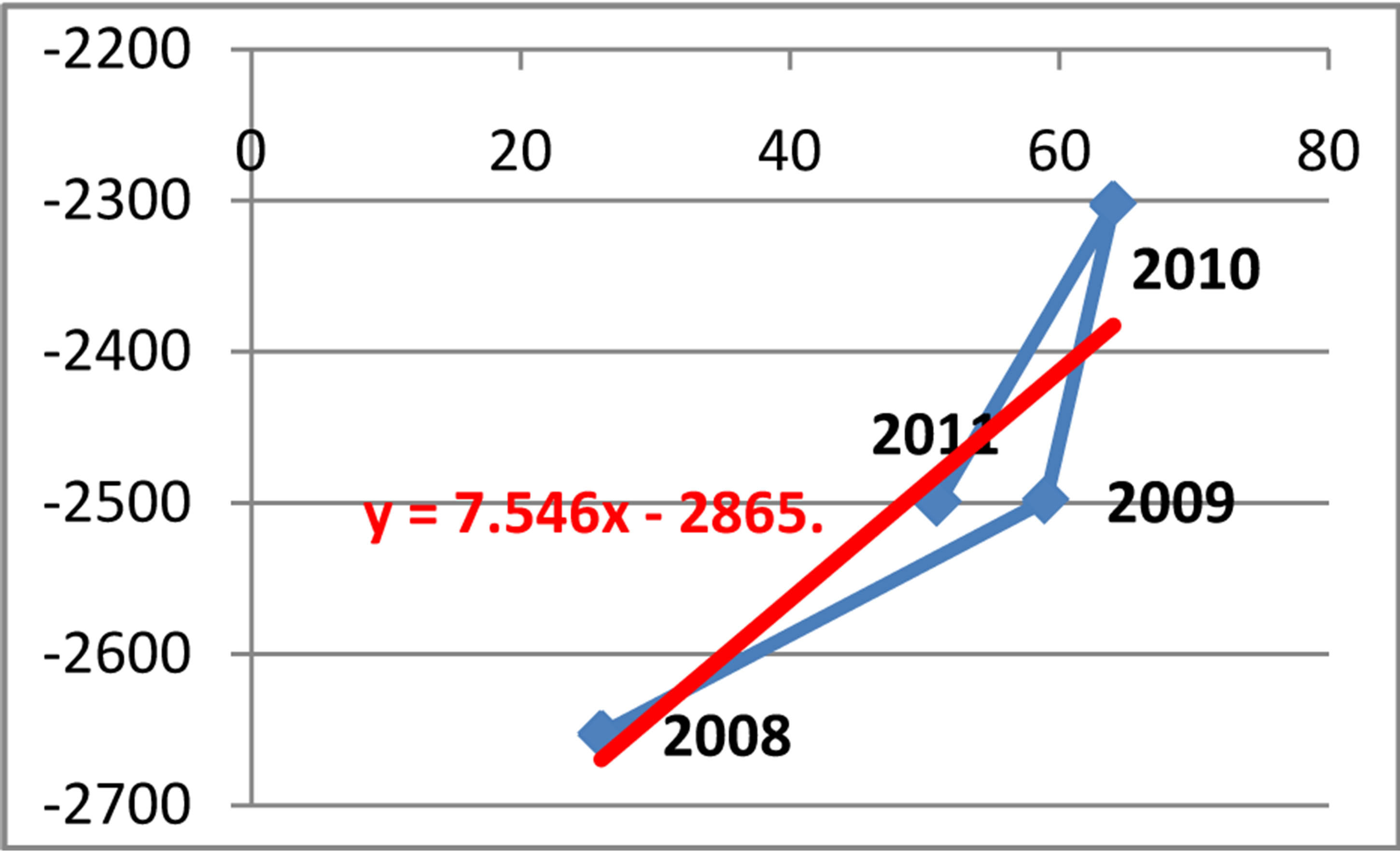
Figure 11. Relationship between net export and cases referred in prosecutor’s office for money laundering.
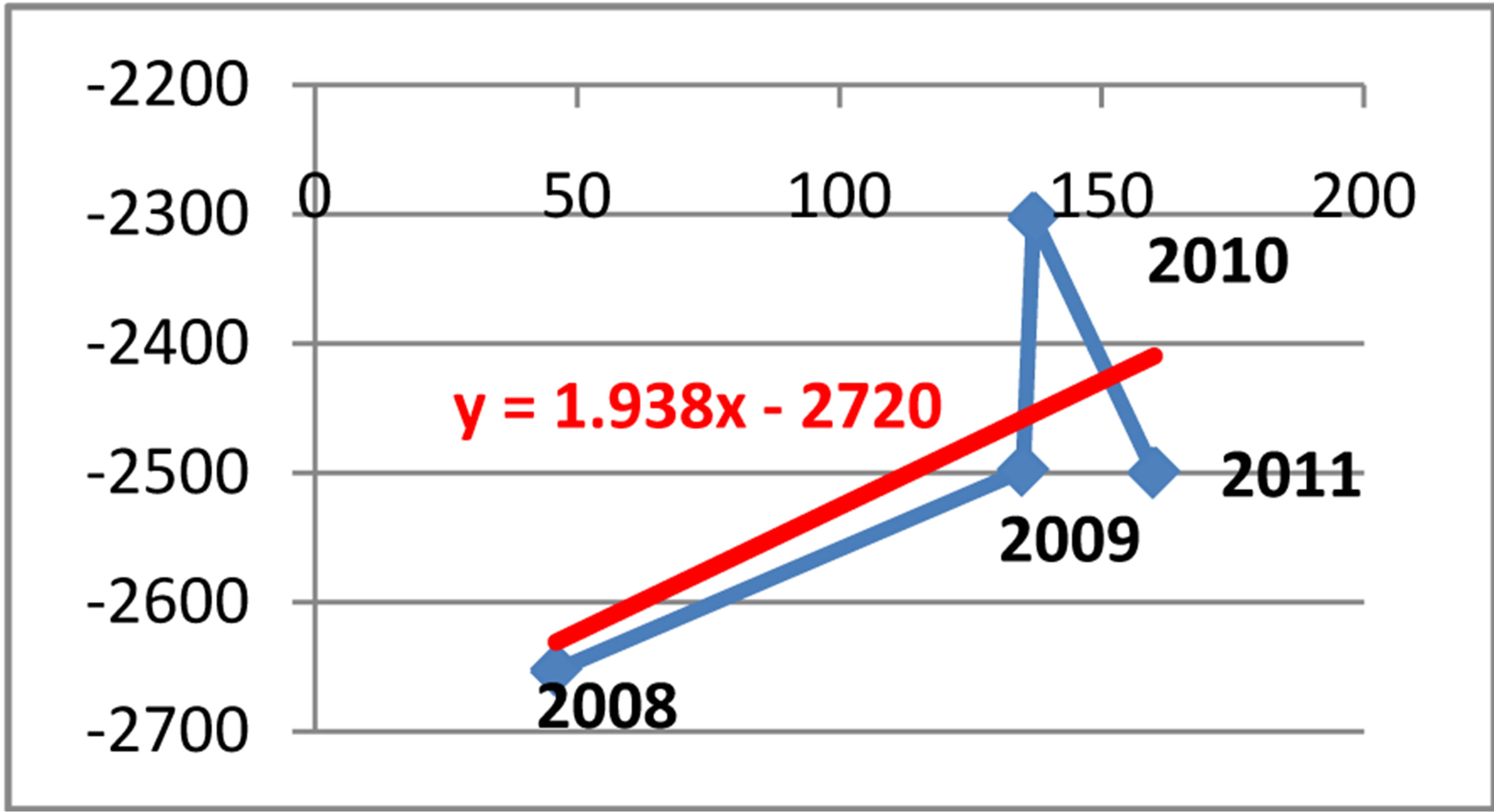
Figure 12. Relationship between net export and cases reported in the police for money laundering during 2008- 2011.
January 2008- December 2011.
In Figure 14 the equation of the linear regression for the cases reported in the police is y = −2.9113 + 0.0011x
where x denotes the cases reported in the police, and y denotes the net export in the Republic of Albania during the period of time January 2008-December 2011.Coefficient of correlation r = 0.64
Coefficient of determination d = 0.41
Equation of linear regression y = −710.73 + 56.307x
Coefficient of correlation r = 0.60
Coefficient of determination d = 0.36
Equation of linear regression y = 13.086 + 0.0026x
Using the regression and correlation analysis we have concluded that there is a relationship between unemployment and cases referred in the prosecutor’s office and reported in the police for money laundering.
The coefficient of correlation is correspondingly r = 0.64 (or r = 0.60), which indicate a moderate positive correlation between the variables. While, the coefficient of determination is respectively d = r2 = 41% (or d = 36%). This result is interpreted in this way: 41% (or 36%) of the total unemployment can be explained by the cases referred in prosecutor’s office (or the ones reported in the police) for money laundering. But, 59% (or 64%) of the total unemployment is explain by other factors, which were not taken in consideration during this study.
In Figure 15 the equation of the linear regression for the cases referred in the prosecutor’s office is y = −710.73 + 56.307x, where x denotes the cases referred in
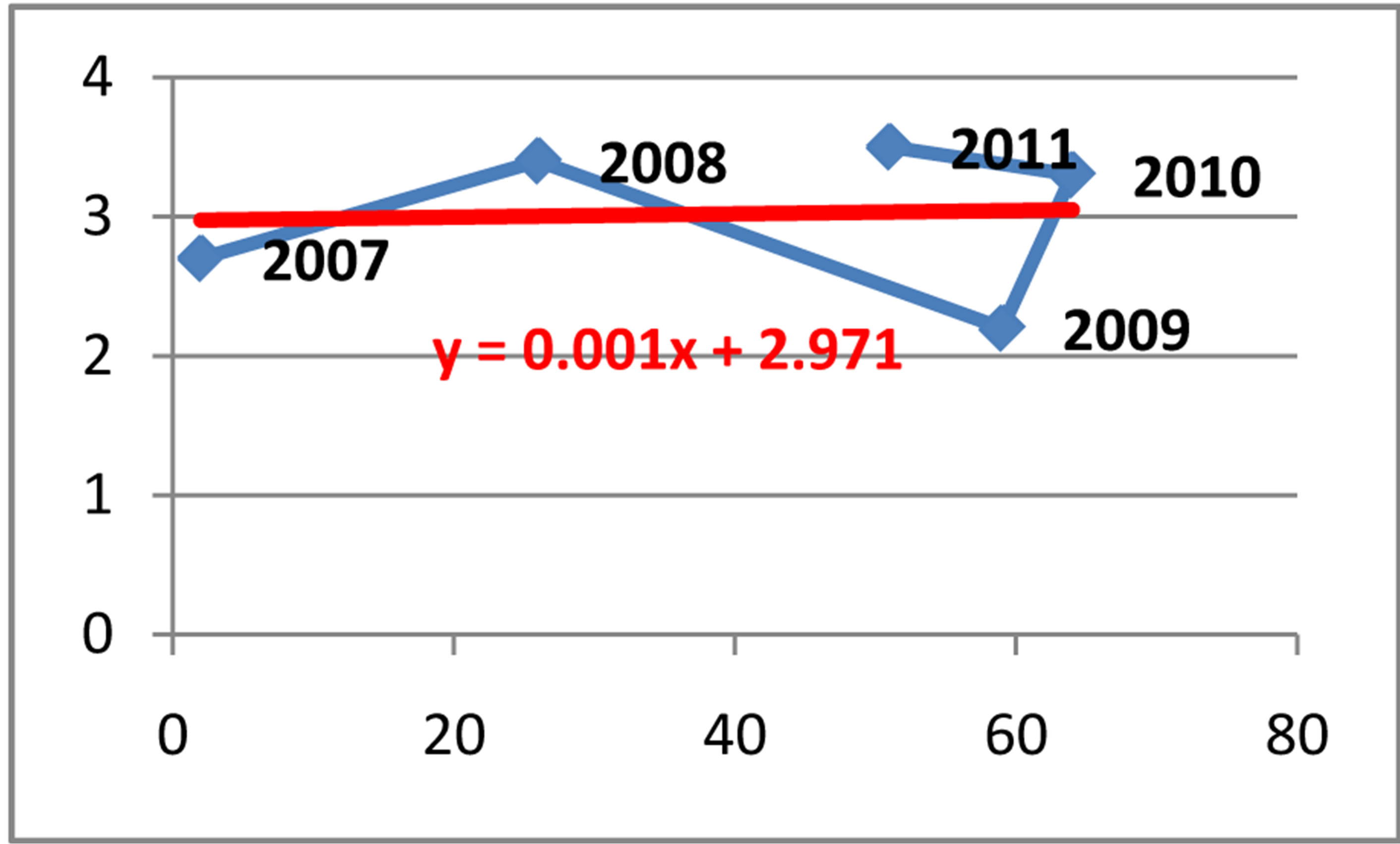
Figure 13. The relationship between the cases referred in the prosecutor’s office and the annual inflation rate in Albania.
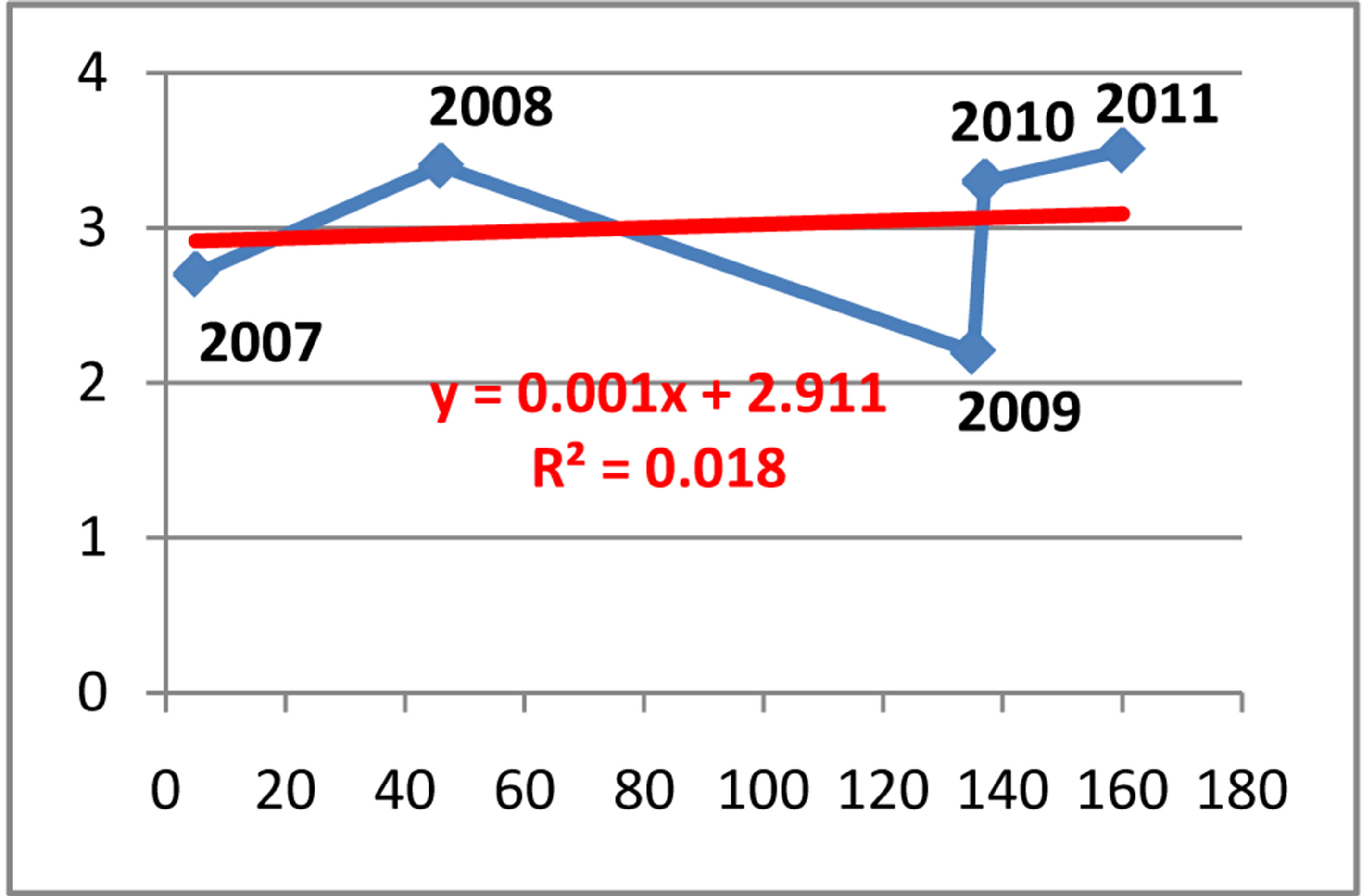
Figure 14. Relation between cases reported in the police for money laundering and the annual inflation rate in Albania.
prosecutor’s office, and y denotes the unemployment in the Republic of Albania during the period of time January 2008-December 2011.
In Figure 16 the equation of the linear regression for the cases reported in the police is y = 13.086 + 0.0026x, where x denotes the cases reported in the police, and y denotes the unemployment in the Republic of Albania during the period of time January 2008- December 2011.
Coefficient of correlation r = −0.979
Coefficient of determination d = 0.9584
Equation of linear regression y = 4909.2 − 78.788x
Coefficient of correlation r = −0.9736
Coefficient of determination d = 0.9479
Equation of linear regression y = 4651.4 − 30.281x
Using the regression and correlation analysis we have concluded that there is a relationship between investments and cases referred in the prosecutor’s office and reported in the police for money laundering. The coefficient of correlation between the cases reported in the prosecutor’s office and investments is r = −0.979, while the relationship between the cases reported in the police and the investments is r = −0.9736, which indicate a strong negative e correlation between the variables. While, the coefficient of determination is respectively d = r2 = 0.9584 or d = 0.9479.
In Figure 17 the equation of the linear regression for the cases referred in the prosecutor’s office is y = 4909.2 − 78.788x, where x denotes the cases referred in prosecutor’s office, and y denotes the unemployment in the Republic of Albania during the period of time January 2008-December 2011.
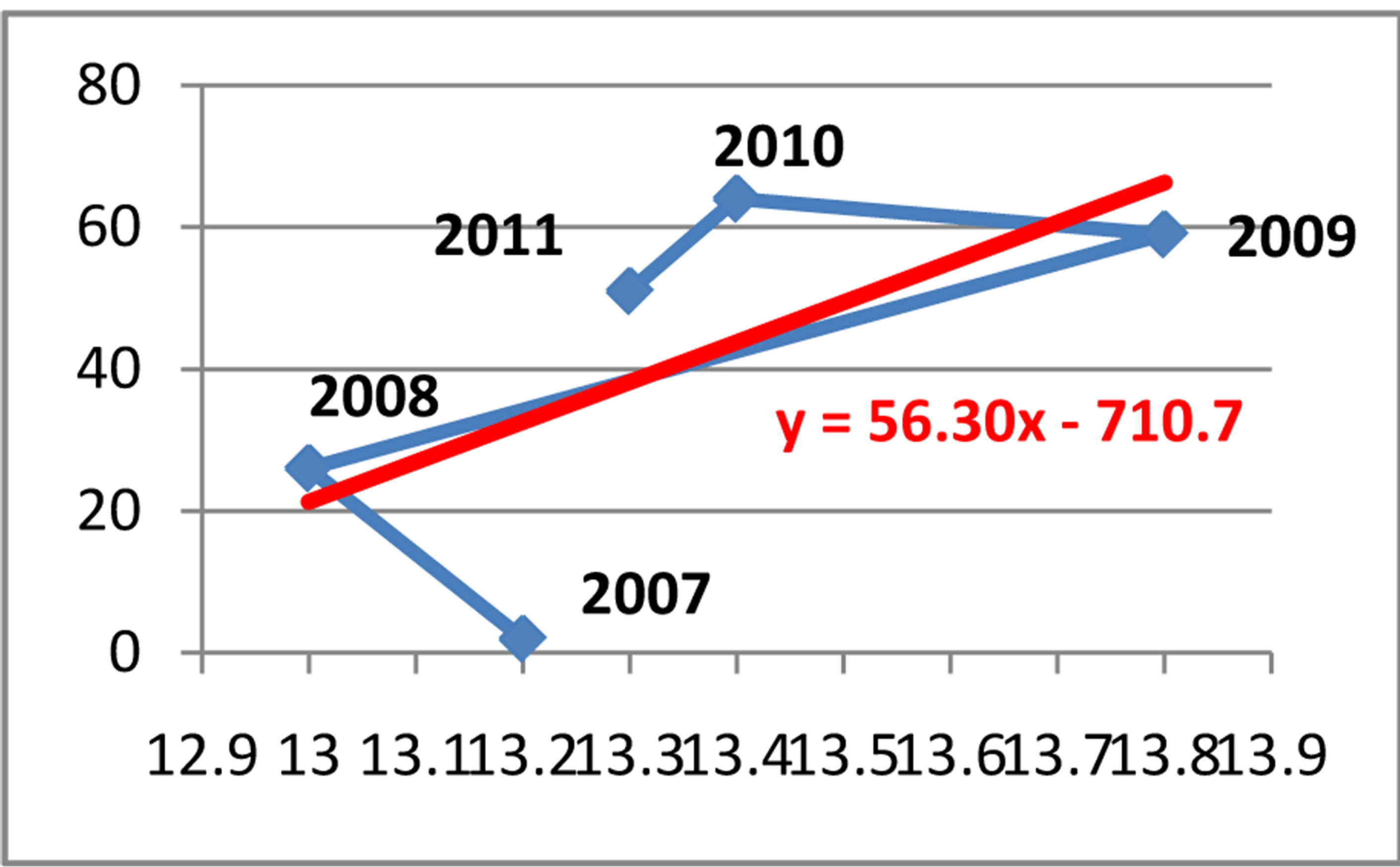
Figure 15. Relationship between cases referred in prosecutor’s office and the annual unemployment rate in Albania.
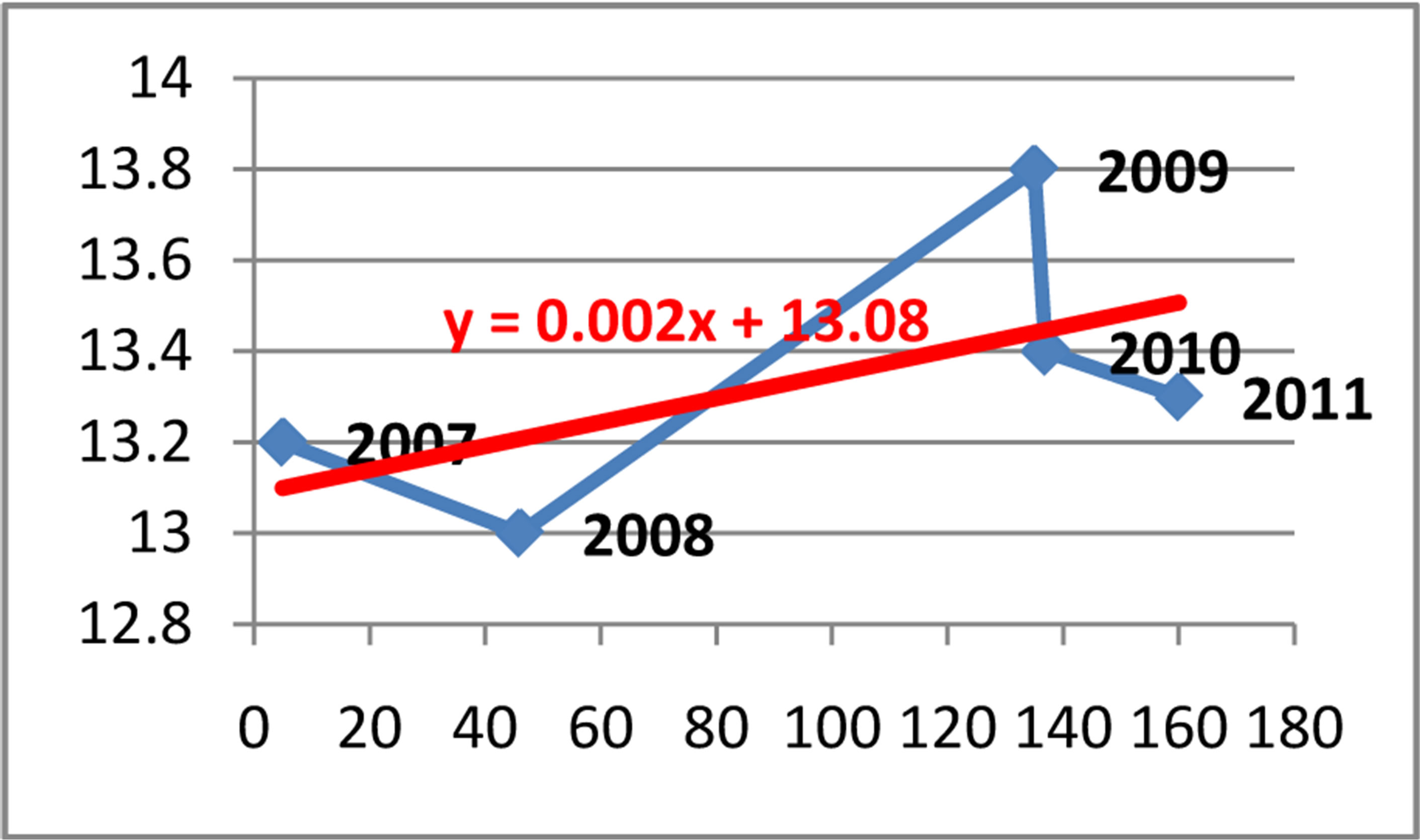
Figure 16. Relationship between cases reported in the police and the annual unemployment rate in Albania.
In Figure 18 the equation of the linear regression for the cases reported in the police is y = 4651.4 − 30.281x, where x denotes the cases reported in the police, and y denotes the unemployment in the Republic of Albania during the period of time January 2008- December 2011.
Coefficient of correlation r = 0.95
Coefficient of determination d = 0.9036
Equation of linear regression y = 501.81 + 4.4008x
Coefficient of correlation r = 0.8941
Coefficient of determination d = 0.7995
Equation of linear y = 525.14 + 1.5989x
Using the regression and correlation analysis we have concluded that there is a relationship between the foreign direct investments and cases referred in the prosecutor’s office and reported in the police for money laundering.
The coefficient of correlation between the cases reported in the prosecutor’s office and the foreign direct investments is r = 0.9505, while the relationship between the cases reported in the police and the foreign direct investments is r = 0.894, which indicate a strong positive correlation between the variables. While, the coefficient of determination is respectively d = r2 = 0.9036 or d = 7995.
In Figure 19 the equation of the linear regression or the cases referred in the prosecutor’s office is y = 501.81 + 4.4008x, where x denotes the cases referred in prosecutor’s office, and y denotes the unemployment in the Republic of Albania during the period of time January 2008-December 2011.
In Figure 20 the equation of the linear regression for the cases reported in the police is y = 525.14 + 1.5989x,
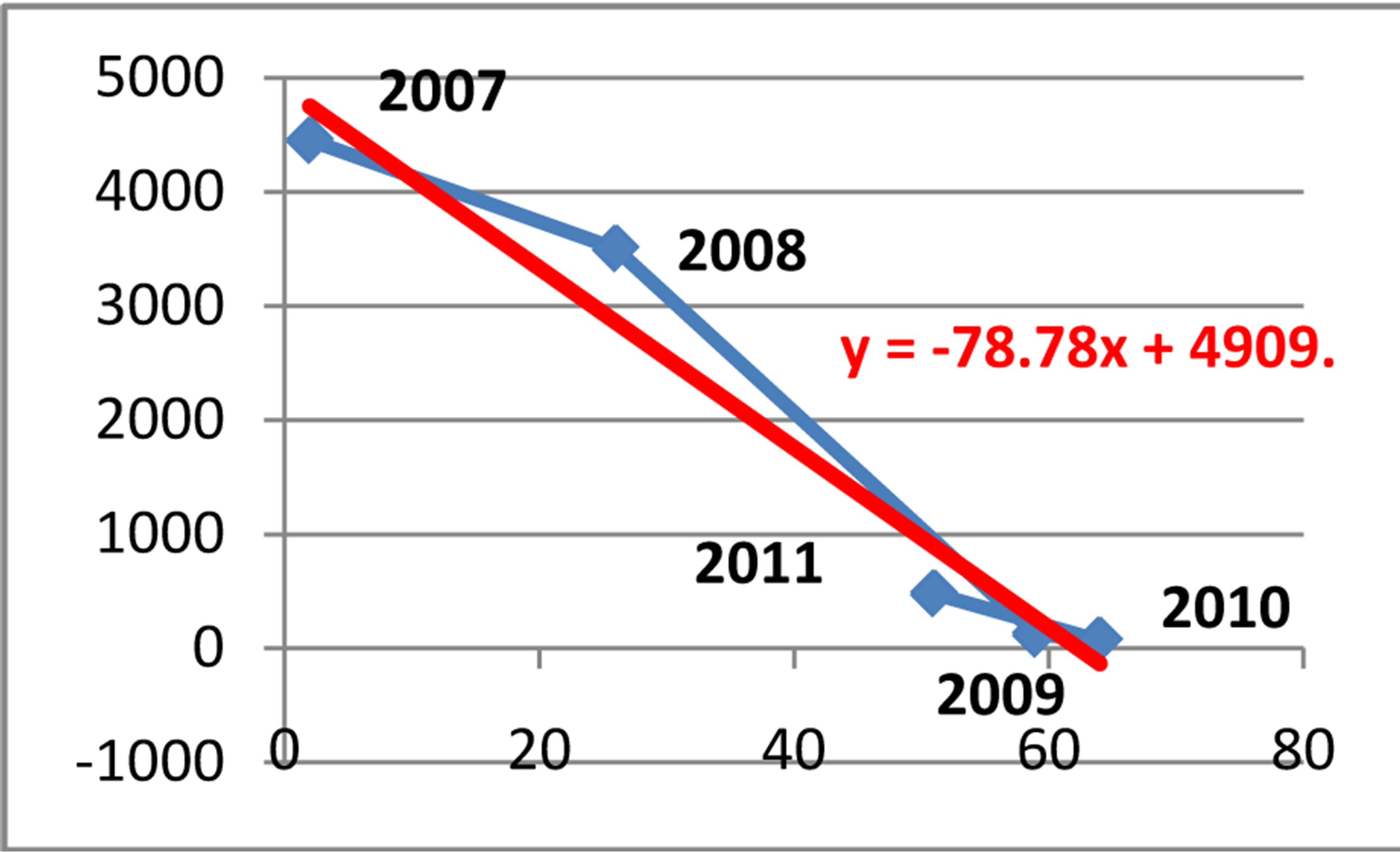
Figure 17. Relation between the cases referred in the prosecutor’s office and the investments in Albania.

Figure 18. Relationship between the cases reported in the police and the investments in Albania.
where x denotes the cases reported in the police, and y denotes the unemployment in the Republic of Albania during the period of time January 2008-December 2011.
The main difficulty (and restriction) of the study is missing of the official data regarding to the money laundering before 2007 in Albania.
Let us reconsider the relationship between the annual number of cases referred in prosecutor’s office for money laundering (denoted by x) and the rate of annual real GDP growth (denoted by y) during the period 1 January 2007-31 December 2011 in Albania.
Given the data set containing n = 5 observations:
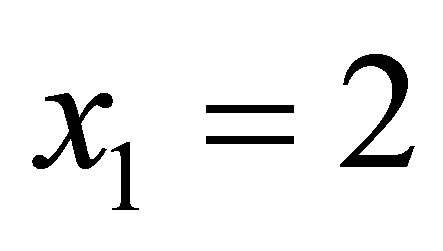 ,
, 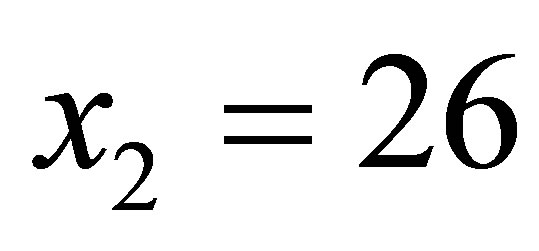 ,
, 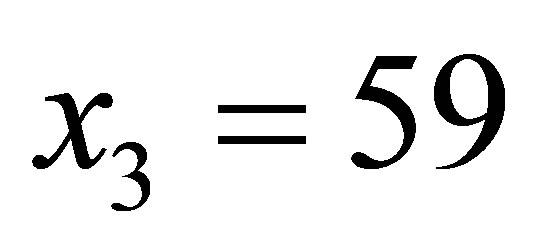 ,
, 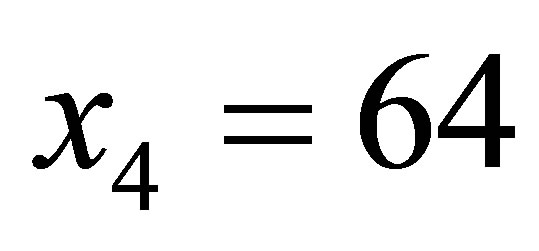 ,
, 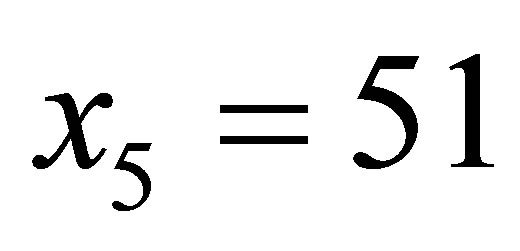 ,
,
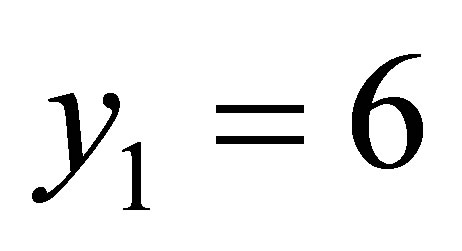 ,
,  ,
, 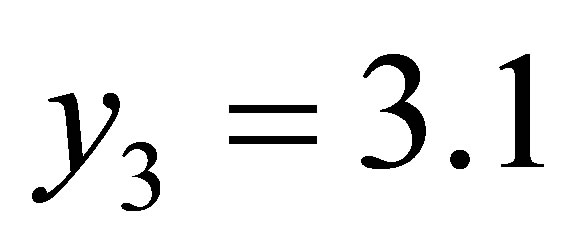 ,
, 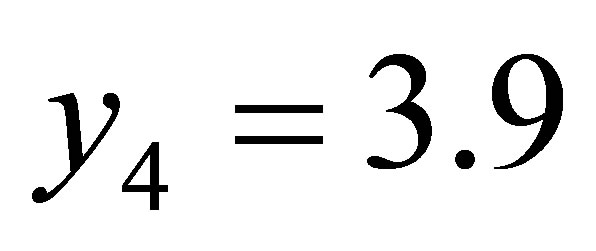 ,
, 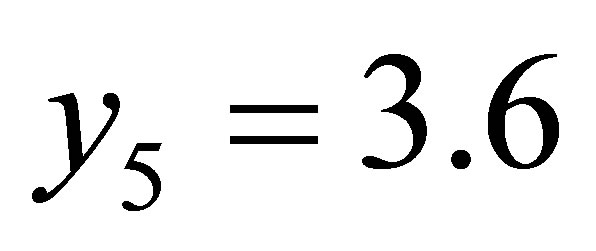 see Table 1.
see Table 1.
Compute the following statistics:

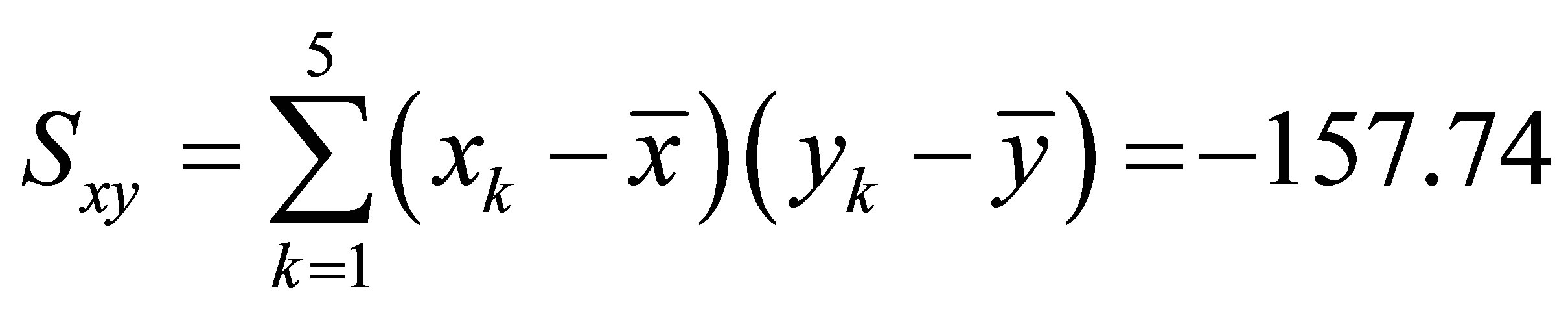 .
.
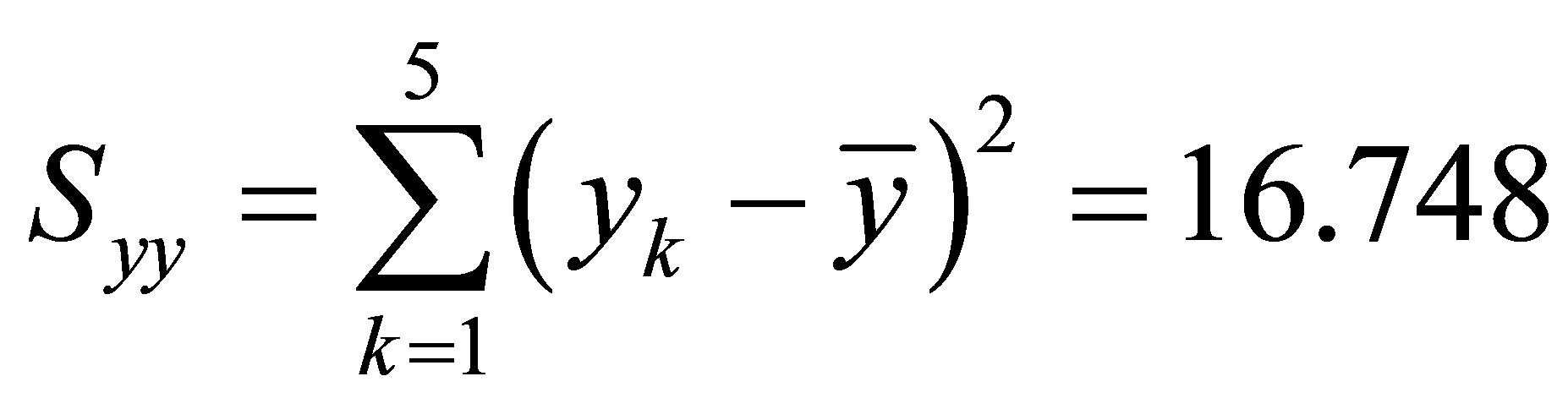 .
.
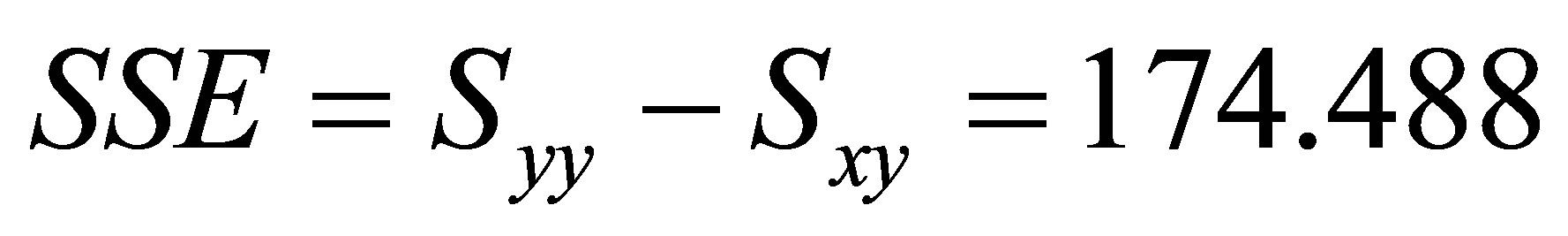
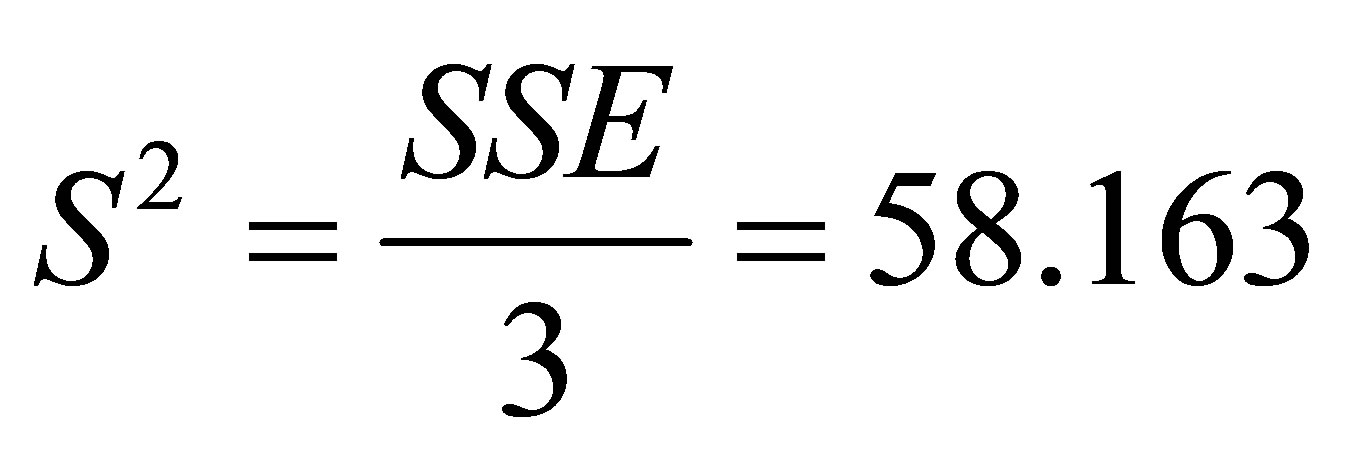 .
.
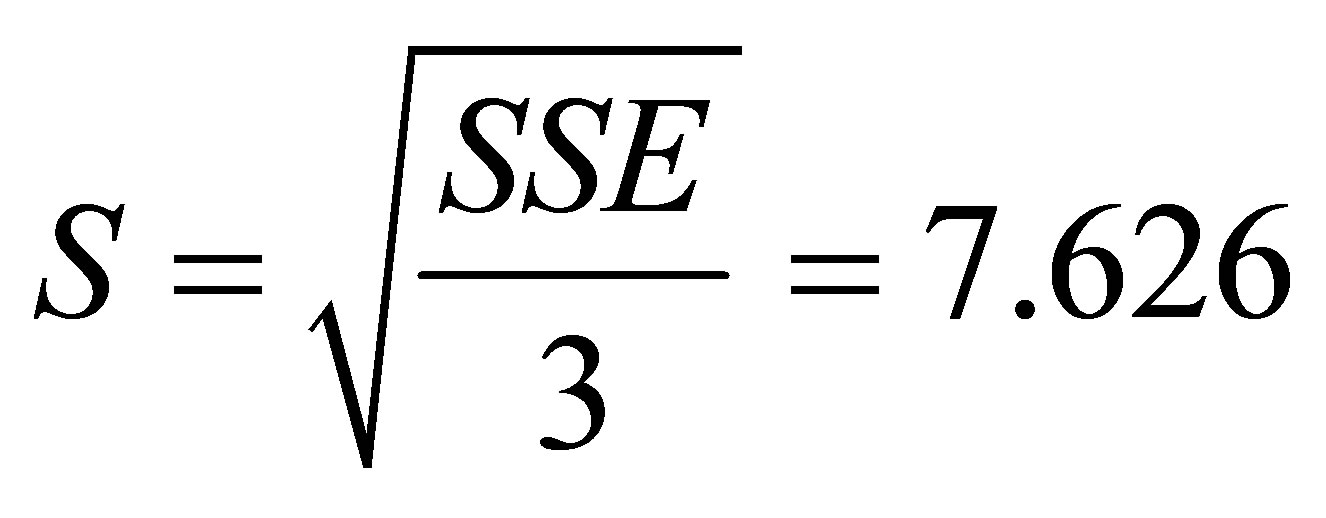

Figure 19. The relationship between cases referred in the prosecutor’s office and the foreign direct investments.
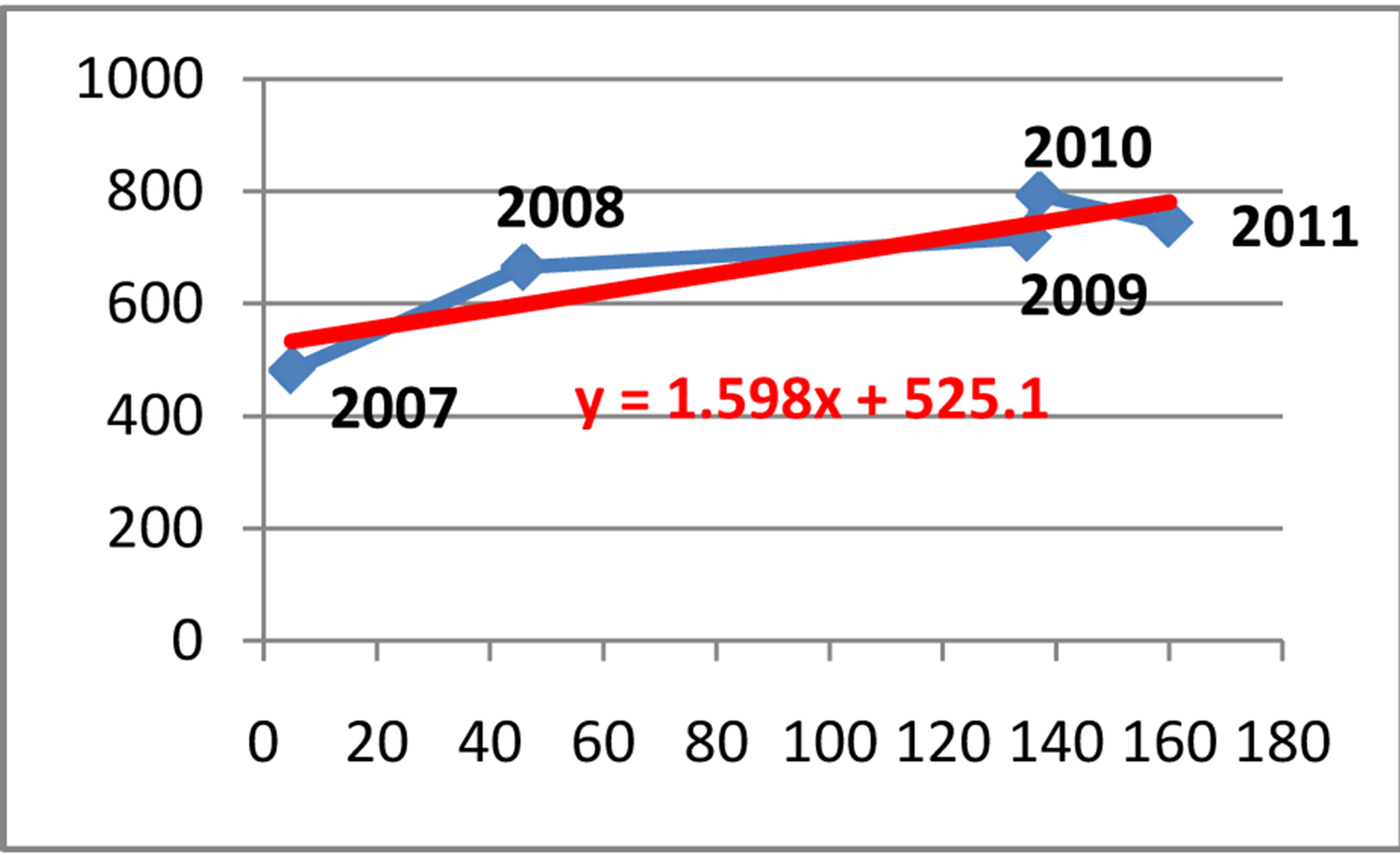
Figure 20. The relationship between cases reported in the police and the foreign direct investments in Albania.
The simple linear regression equation is
 where ε denotes the random error term, see Bolton and David (2002).
where ε denotes the random error term, see Bolton and David (2002).
Assume that the mean 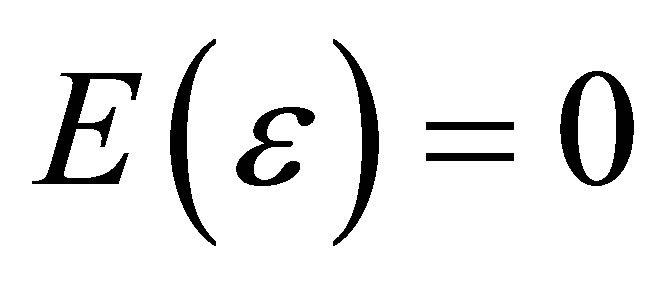 and the variance
and the variance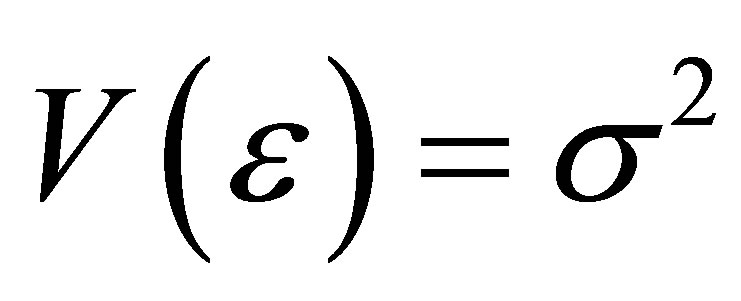 . An estimation of the unknown variance
. An estimation of the unknown variance 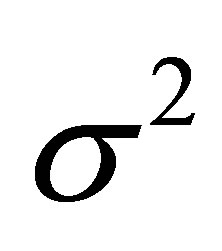 is
is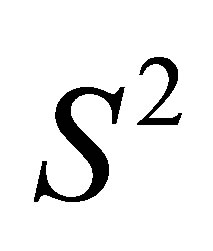 . If the random error ε is normally distributed, then both
. If the random error ε is normally distributed, then both  and
and  are normally distributed. Furthermore, the random variable
are normally distributed. Furthermore, the random variable 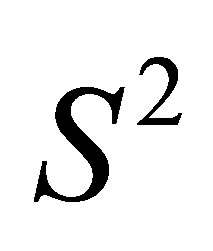 is independent of both
is independent of both 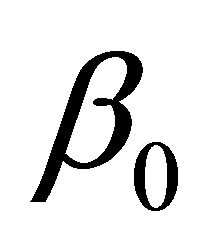 and
and .
.
Compute: 
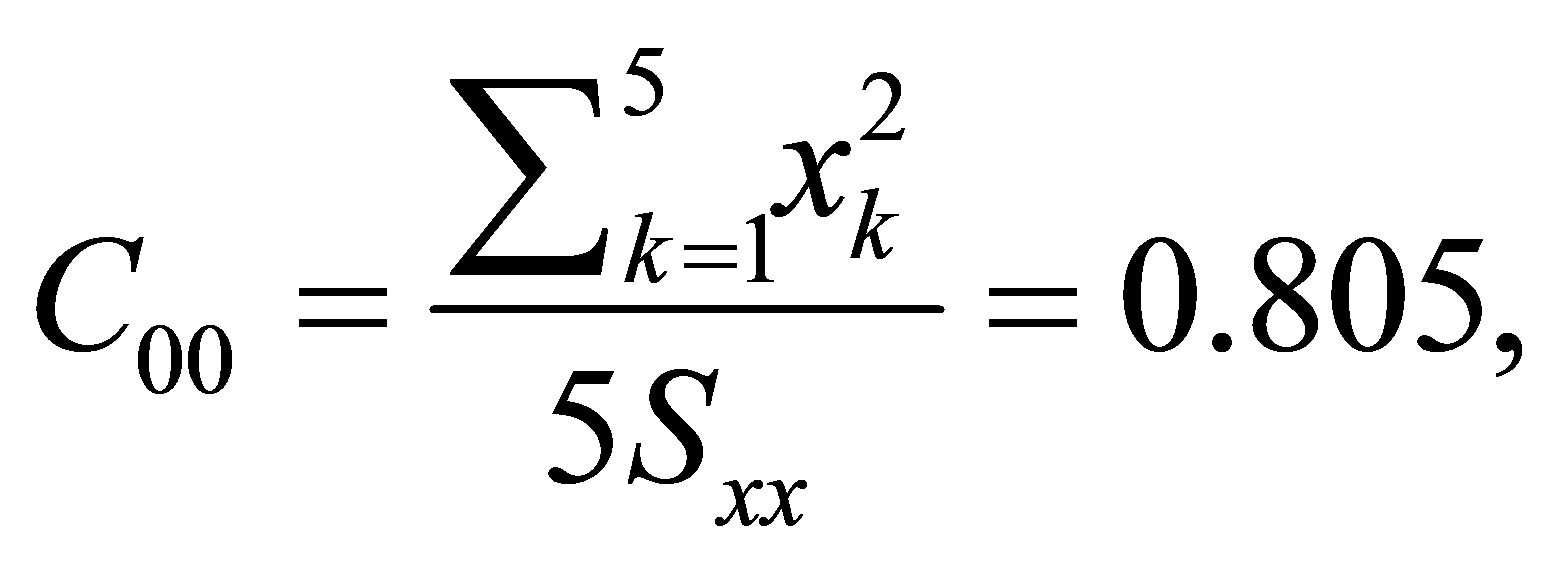
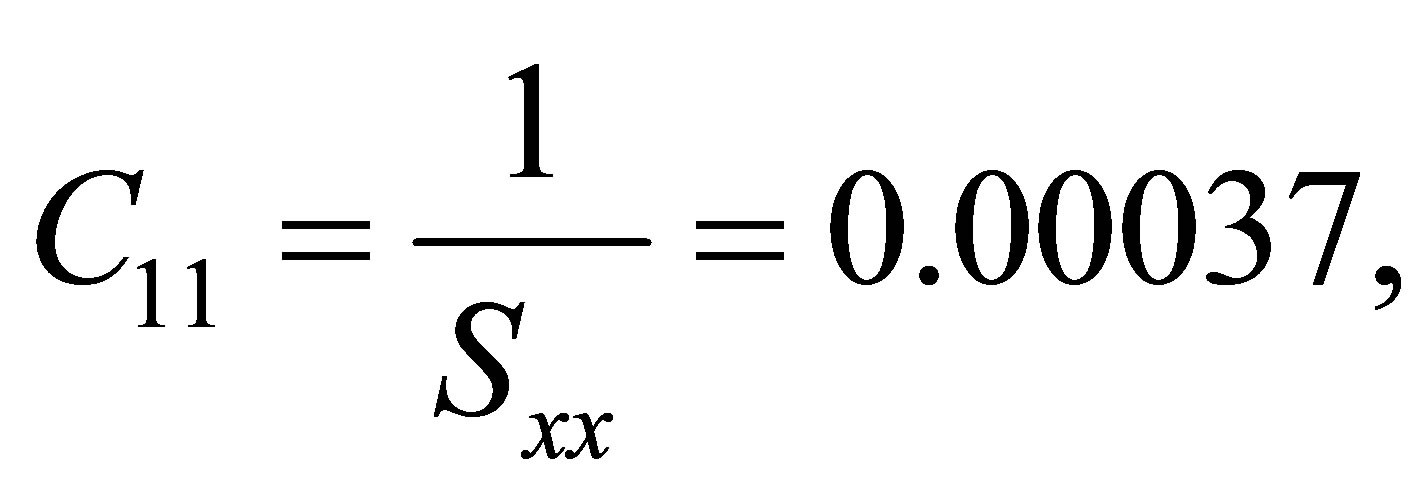
and the critical value of t-distribution
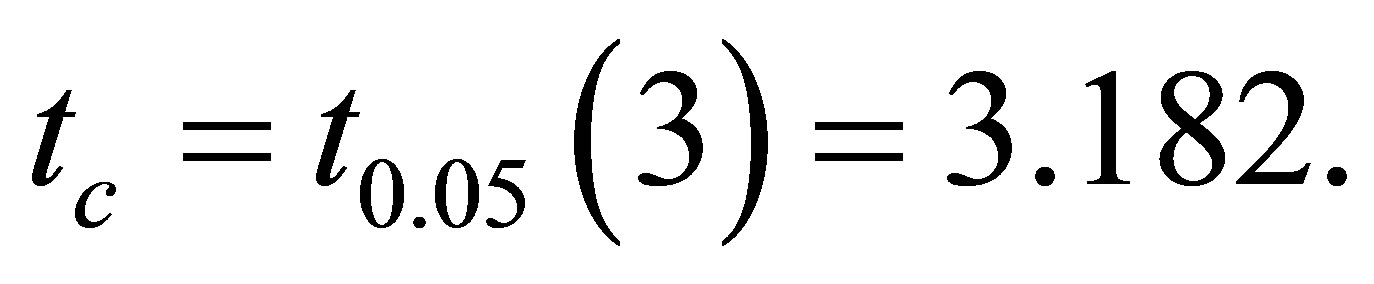
A 95% confidence interval for 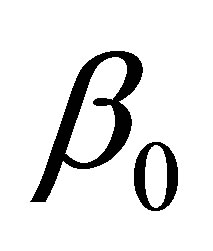 is
is
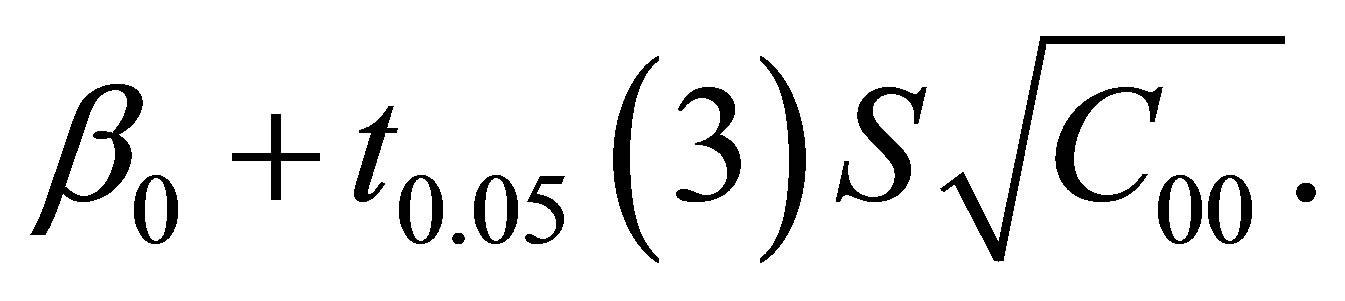
A 95% confidence interval for  is
is
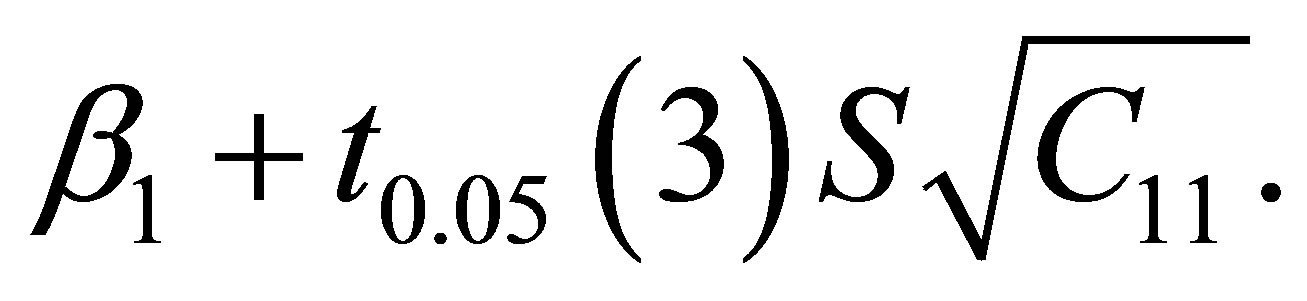 .
.
We obtain the following results:
P (−14.49 < 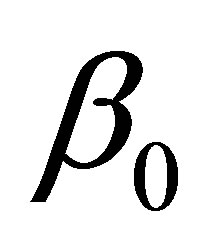 < 29.05) = 95%
< 29.05) = 95%
P (−0.5251 <  < 0.4081) = 95%.
< 0.4081) = 95%.
Given the significance level α = 0.05
Test the hypothesis
H0:  = 0
= 0
Ha: ≠ 0. (two - tailed test)
≠ 0. (two - tailed test)
The appropriate test statistics is “Student’s” t-distribution
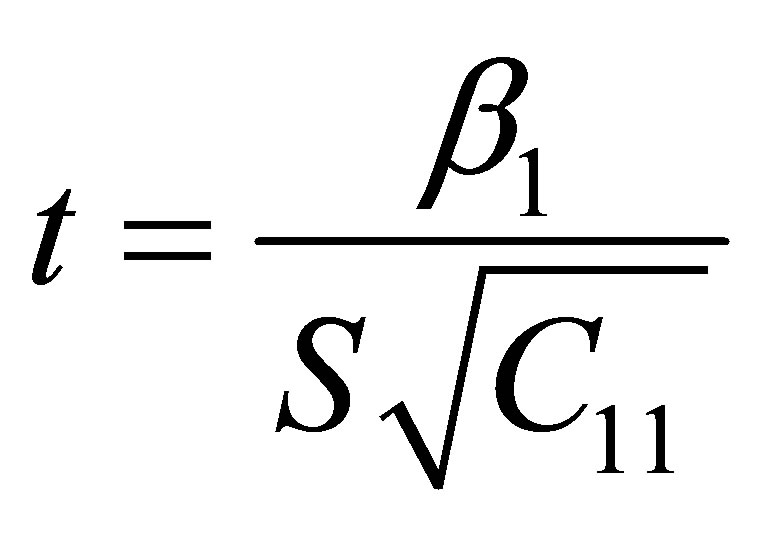
The observed value of the test statistics is

and the critical value of the test statistics is 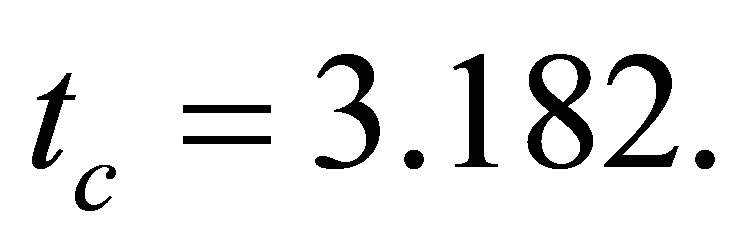
Decision Rule:
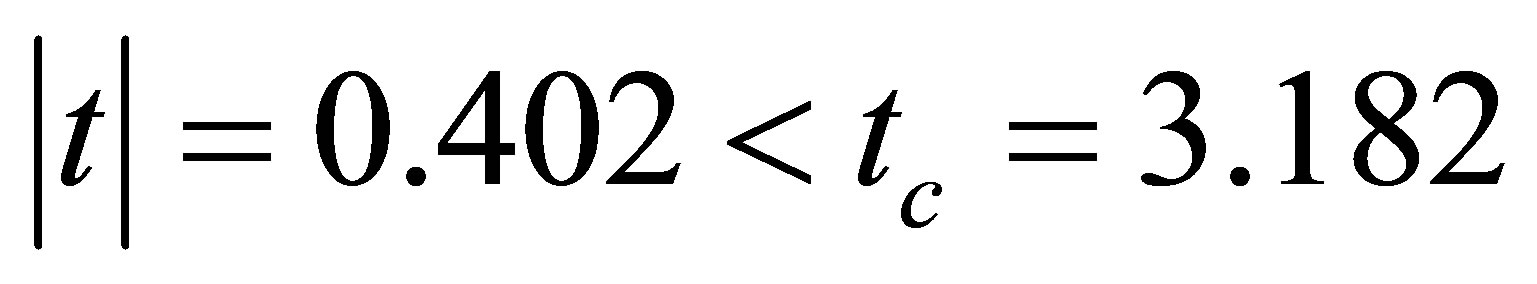
Accept the null hypothesis H0: β1 = 0 at the 95% confidence level.
A 95% confidence interval for the expected value
 where
where 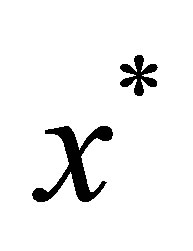 denotes a particular value of x, is given by the formula:
denotes a particular value of x, is given by the formula:
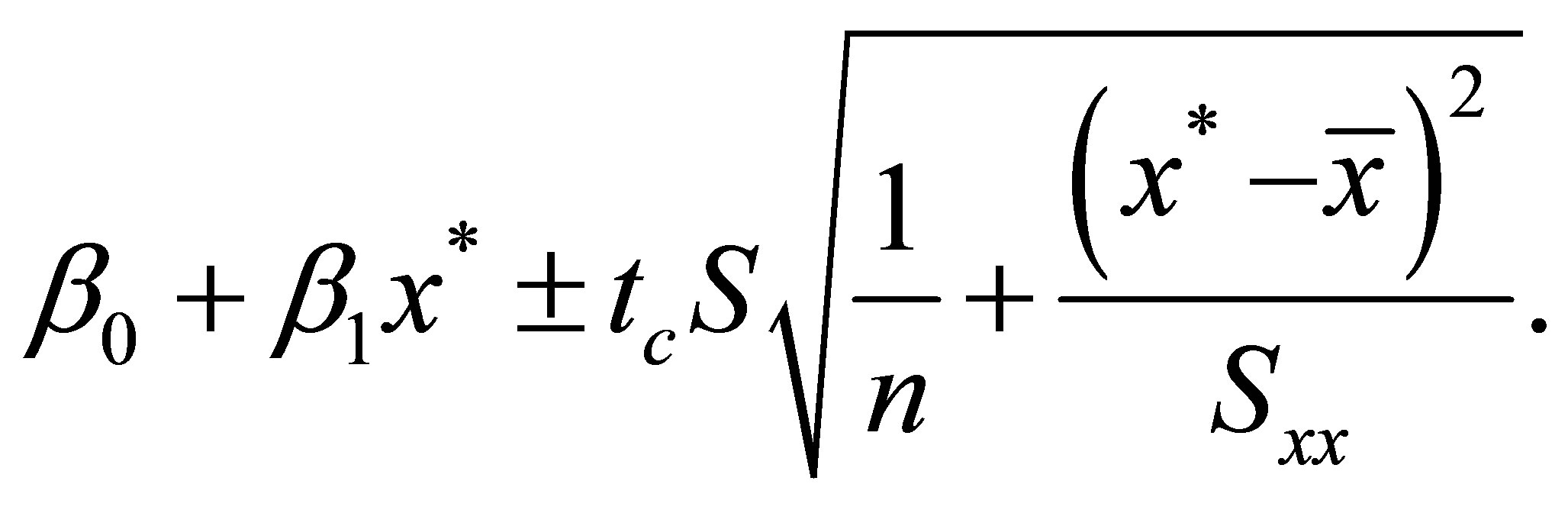
see [5].
We obtain:
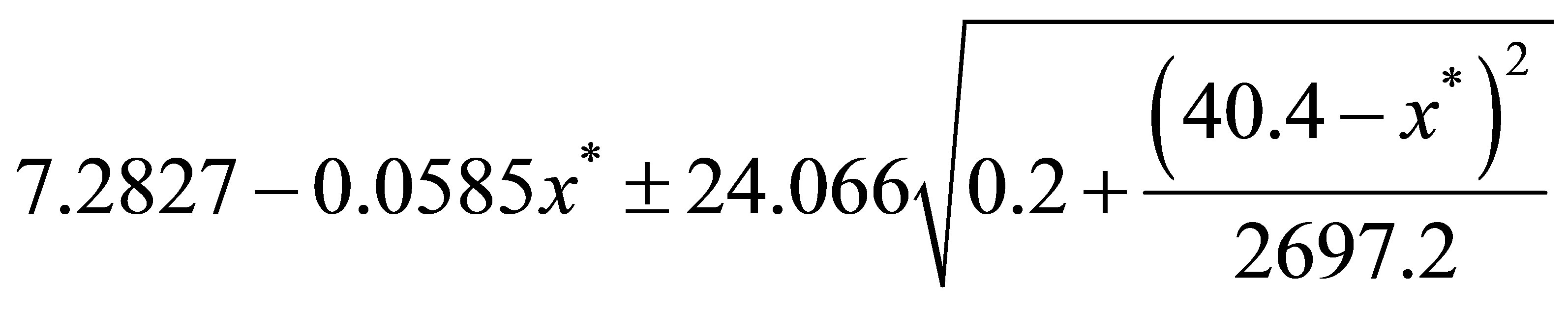
A 95% prediction interval for y when x = x* is given by the formula:
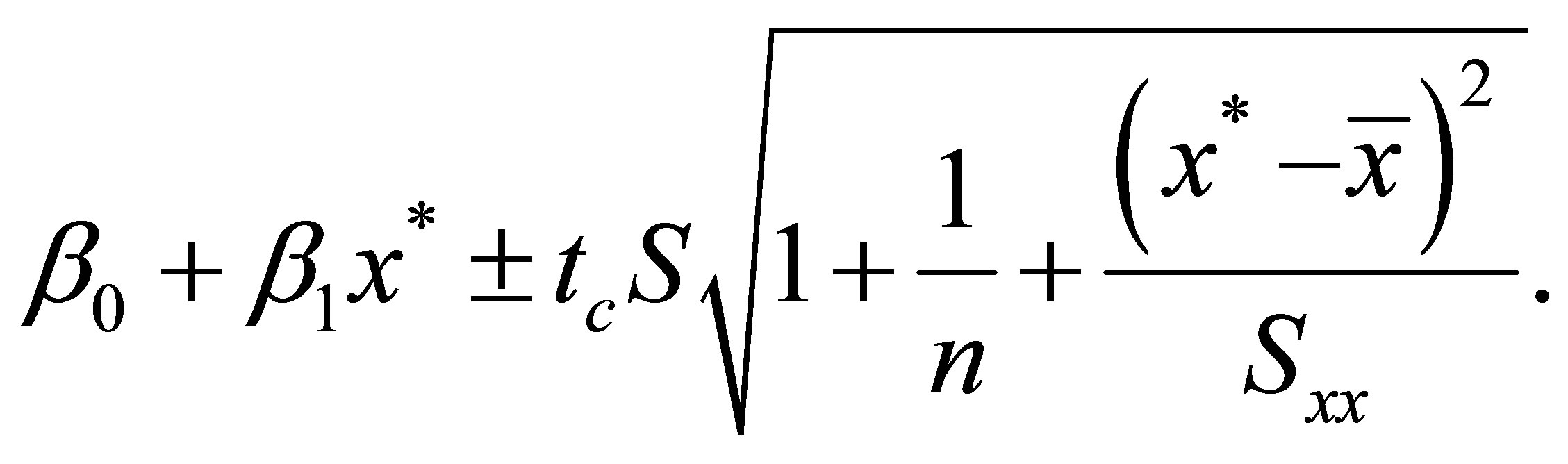
see [5].
We obtain the following results:
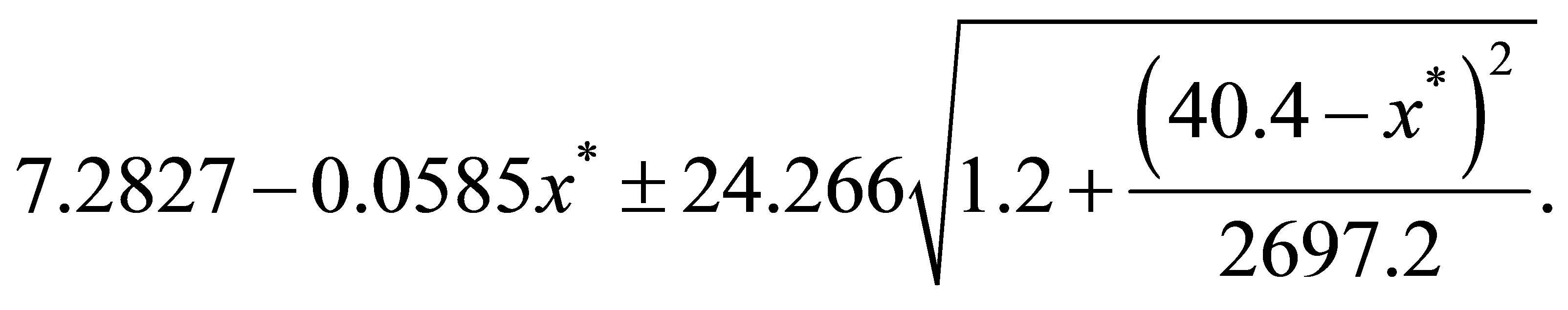
Let consider the relationship between the annual number of cases reported in the police for money laundering (denoted by x) and the rate of annual real GDP growth (denoted by y) during the period 1 January 1997- 31 December 2011 in Albania, see Table 1.
Given the data set containing n = 5 observations:
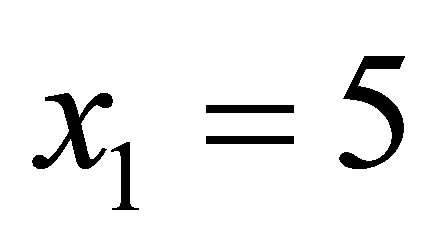 ,
, 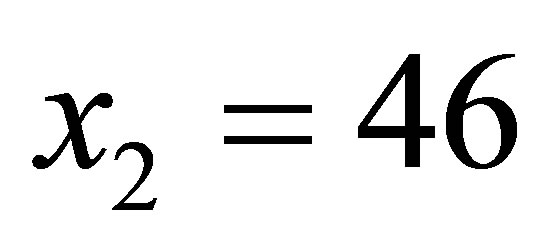 ,
, 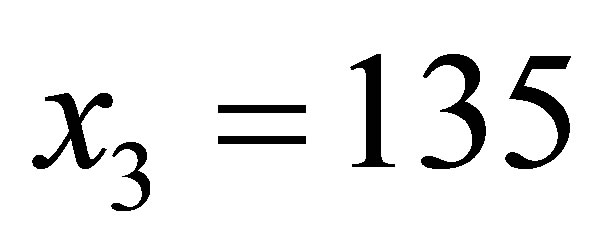 ,
, 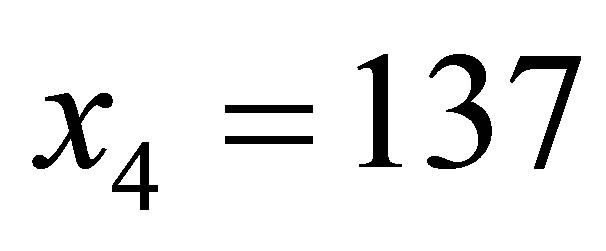 ,
,  ,
,
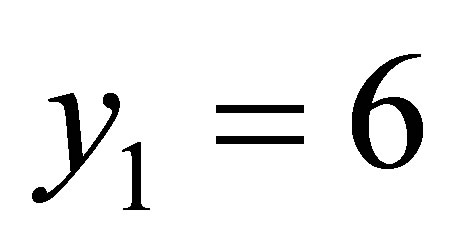 ,
, 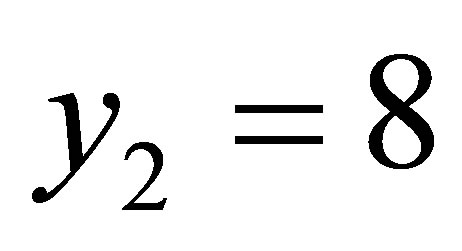 ,
, 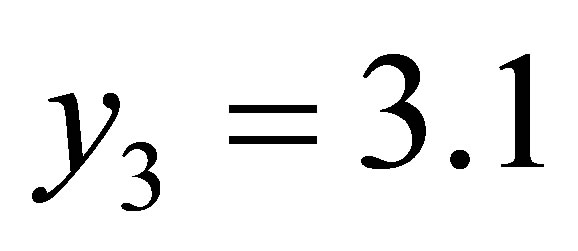 ,
, 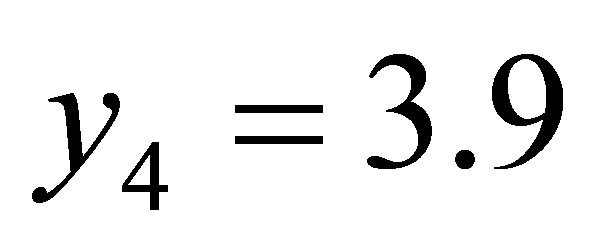 ,
, 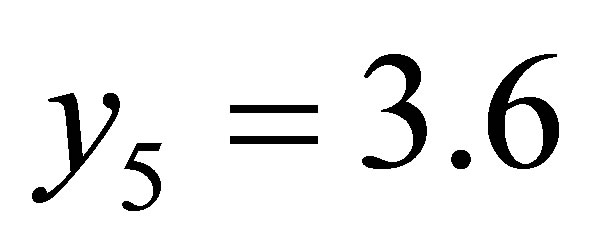
Compute:
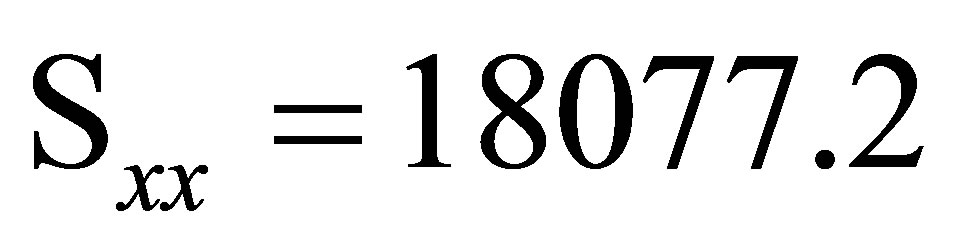 ,
,
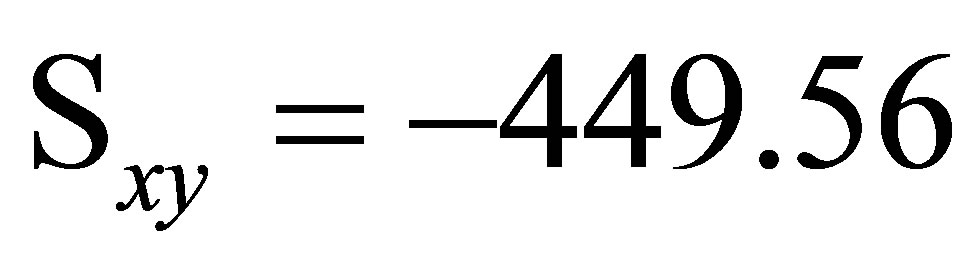 ,
,
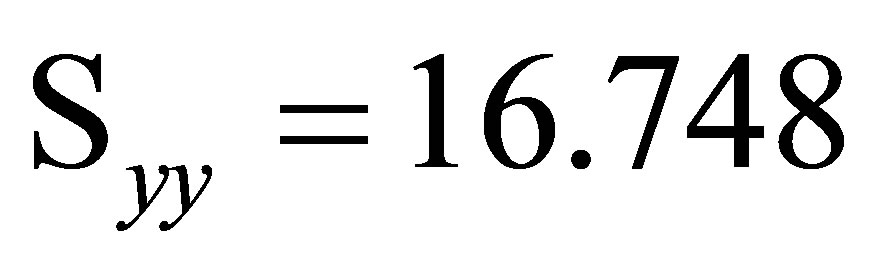 ,
,
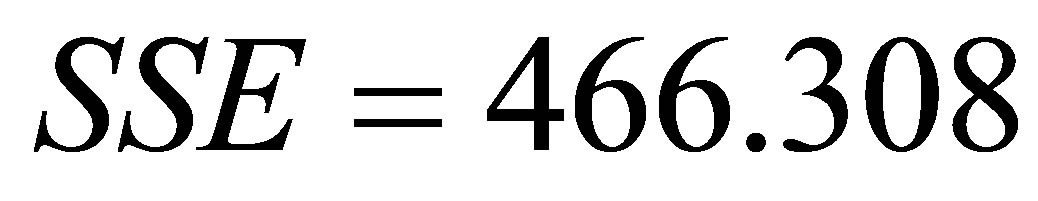 ,
,
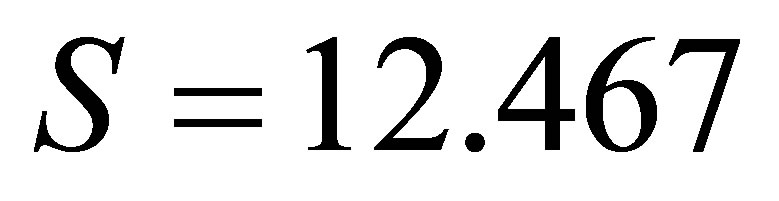 ,
, 
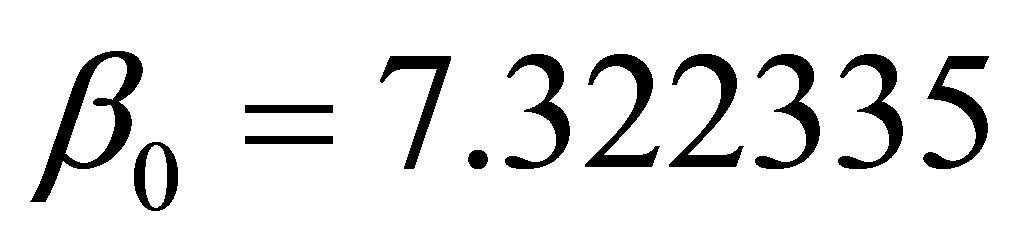 ,
, 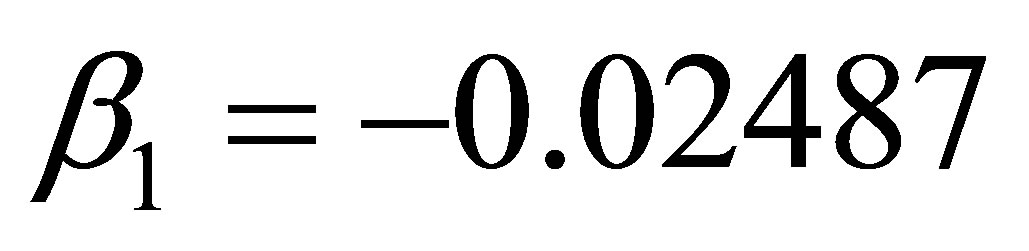 ,
,
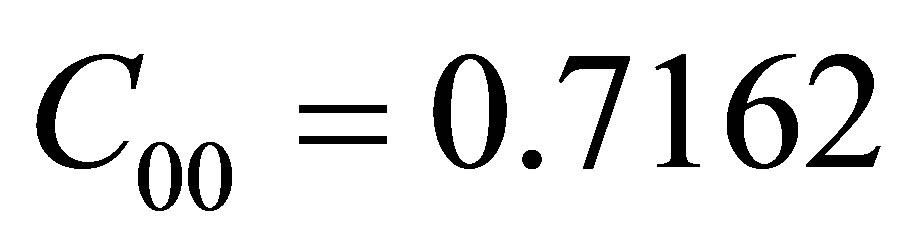 ,
, 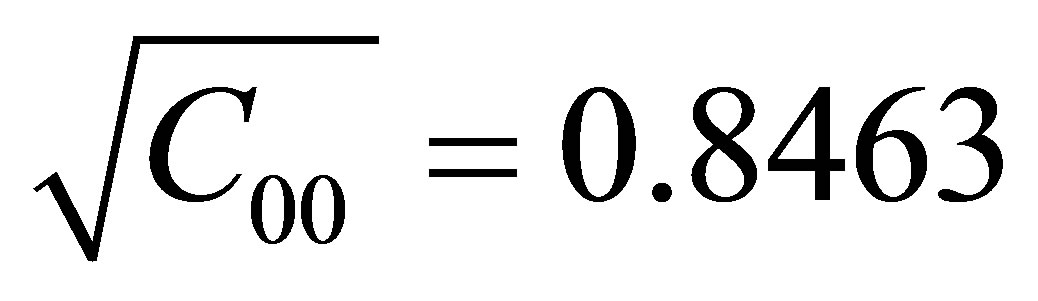 ,
,
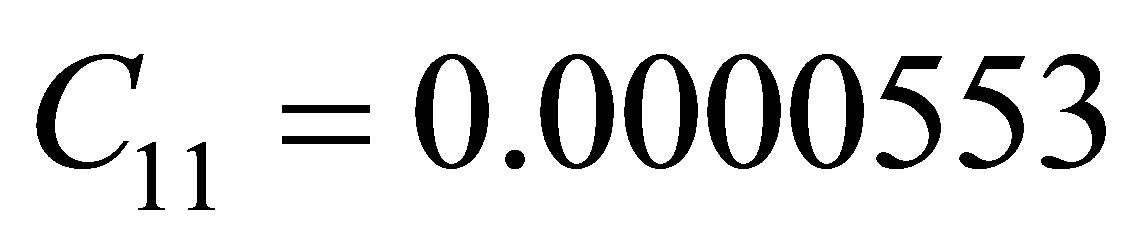 ,
, 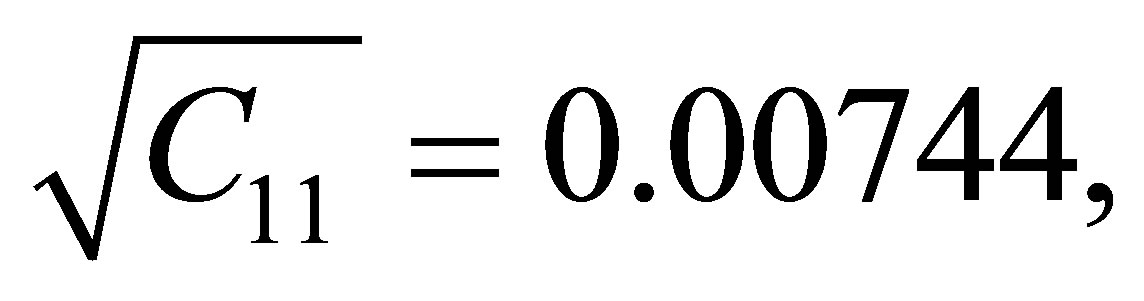
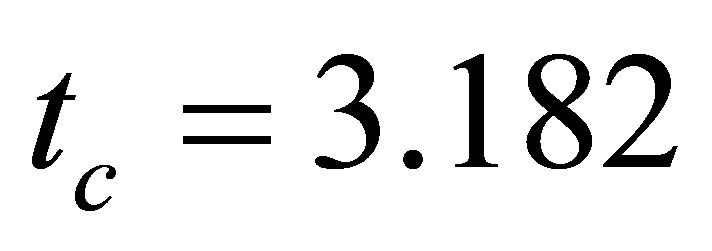 .
.
A 95% confidence interval for 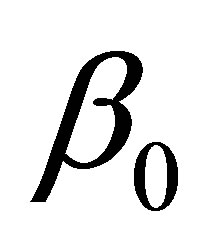 is :
is :
(−26.248; 40.892 ).
A 95% confidence interval for  is :
is :
(−0.320; 0.270 ).
Given the significance level α = 0.05.
Test the hypothesis H0: β1 = 0 Ha: β1 ≠ 0. (two - tailed test)
The observed value of the test statistics is
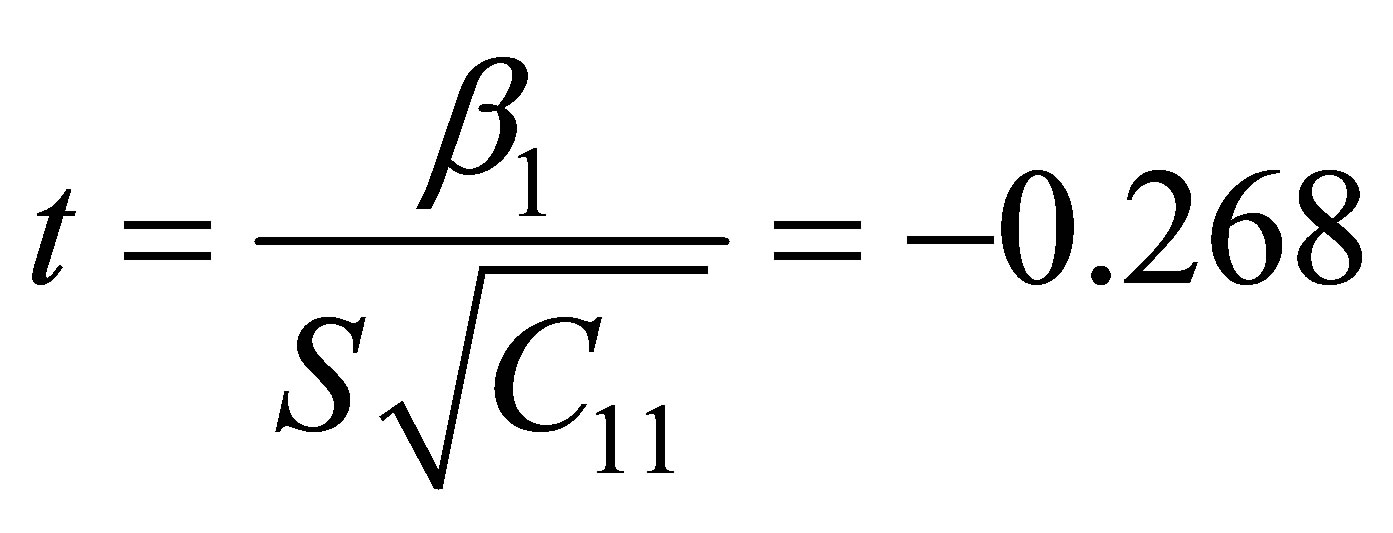
The critical value of the test statistics is

Decision Rule
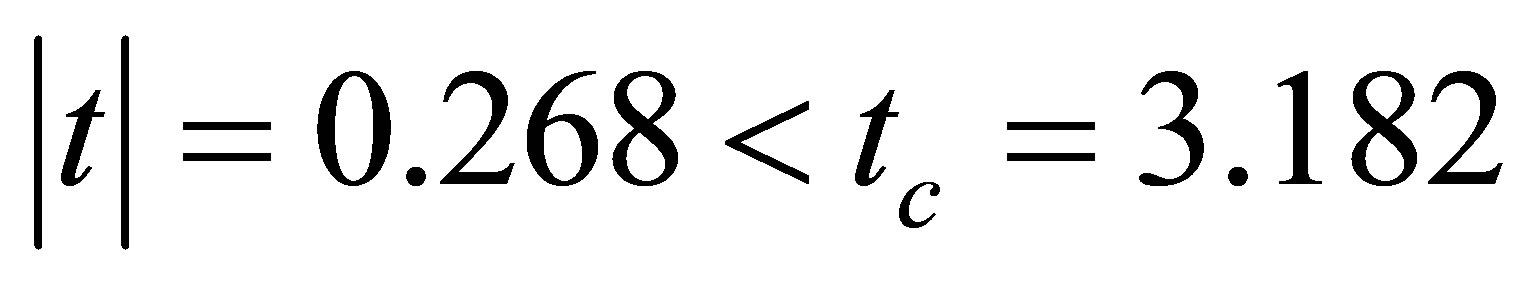
Accept the null hypothesis H0: β1 = 0 at the 95% level of confidence.
A 95% confidence interval for the expected value
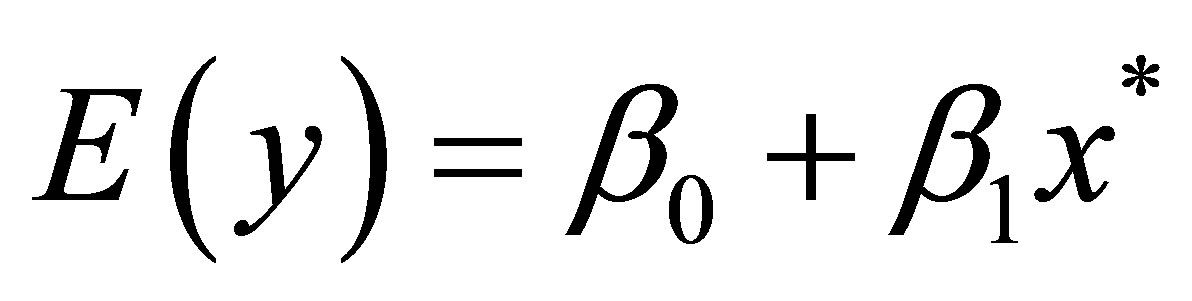 where x* denotes a particular value of x is
where x* denotes a particular value of x is
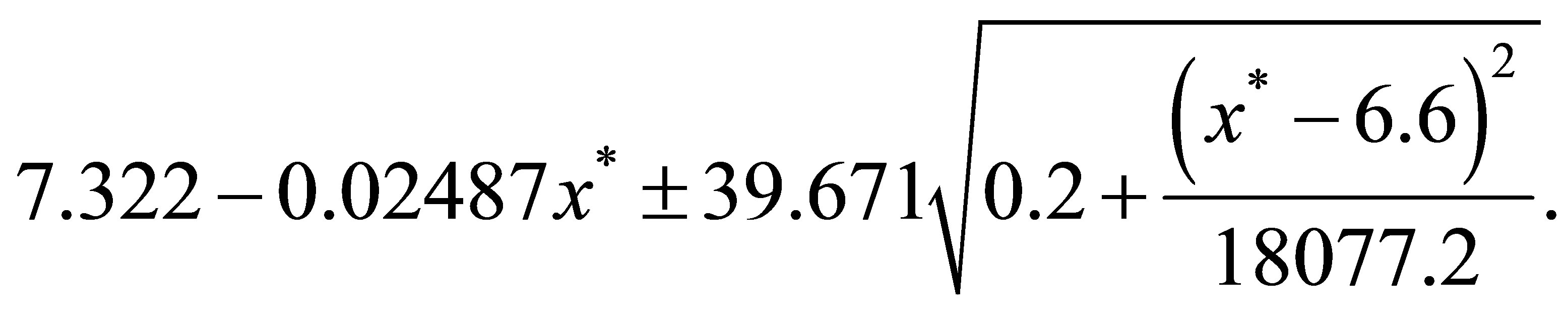
A 95% prediction interval for y
when x = x* is given by the formula
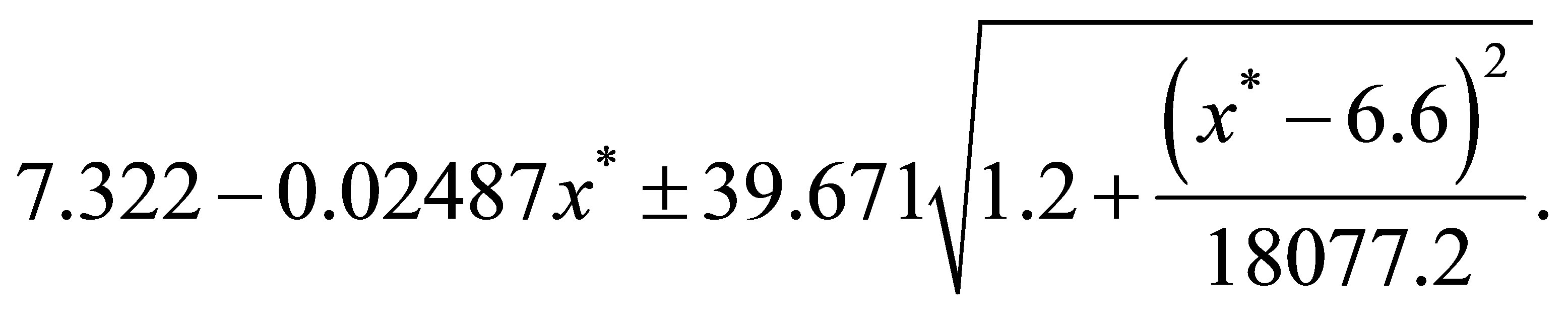
Similarly, we can develop the confidence intervals and hypothesis testing for the parameters β0 and β1 of simple linear regression equation in all relationships considered in the paper.
Remark
The probability distribution for Pearson coefficient of correlation r is difficult to obtain in the small sample case. For large random samples this difficulty could be overcome by using the Fisher z - transformation, see [5].
4. Conclusions
By analyzing the official data available to us during the period of 2007-2011 for the Republic of Albania, it is possible to conclude that the economic growth is negatively correlated with the number of cases of money laundering, because as we have seen in the cases above mentioned the coefficient of correlation “r” is a negative number. However, further researches may be necessary to draw light on this topic, as we had no access to data regarding the exact amount of money laundering. The only information available to us was the number of cases of money laundering. With this information at our disposal, it is not possible to clearly state the percentage that illicit money occupies on the annual GDP growth rate over January 2007-December 2011. Actually, in other countries, these data are published and available for scientific studies, for instance, in America, Germany, and other 11 countries that have done similar researches. But, in Albania the amount of money laundering is not of public domain. Nevertheless, in our case, where the correlation between the two variables X and Y is negative, anti-money laundering policies discourage criminal activities.
Some surprising results of this study are:
1) The positive correlation between government expenditure and the number of cases referred in the prosecutor’s office for money laundering (r = 0.72);
2) The positive correlation between government expenditure and the number of cases reported in police for money laundering (r = 0.79);
3) The positive correlation between export and the number of cases referred in the prosecutor’s office for money laundering (r = 0.17);
4) The positive correlation between export and the number of cases reported in police for money laundering (r = 0.50);
5) The positive correlation between the number of cases referred in the prosecutor’s office for money laundering and net export (r = 0.89);
6) The positive correlation between the number of cases reported in police for money laundering and net export (r = 0.68);
7) The positive correlation between the number of cases referred in the prosecutor’s office for money laundering and annual unemployment rate (r = 0.64);
8) The positive correlation between the number of cases reported in the police and the annual unemployment rate (r = 0.60);
9) The positive correlation between the number of cases referred in the prosecutor’s office for money laundering and the inflation rate (r = 0.22);
10) The positive correlation between the number of cases reported in the police and the inflation rate (r = 0.136);
11) The positive correlation between the number of cases referred in the prosecutor’s office for money laundering and the foreign direct investments in Albania (r = 0.95);
12) The positive correlation between the number of cases reported in the police and the foreign direct investments in Albania (r = 0.8941).
Actually, it is not possible to give a scientific argument for these surprising results, because officially data for the exact amount of money laundering during the years 2007, 2008, 2009, 2010, and 2011 are not published in the Republic of Albania.
REFERENCES
- J. Ferweda, “The Economics of Crime and Money Laundering: Does Anti-Money Laundering Policy Reduce Crime?” Review of Law & Economics, Vol. 5, No. 2, 2008. http://ideas.repec.org/p/use/tkiwps/0835.html
- F. G. Schneider, “Turnover of Organized Crime and Money Laundering: Some Preliminary Empirical Findings,” Public Choice, Vol. 144, No. 3, 2010, pp. 473-486. http://EconPapers.repec.org/RePEc:kap:pubcho:v:144:y:2010:i:3:p:473-486
- R. J. Bolton and D. J. David, “Statistical Fraud Detection: A Review,” Institute of Mathematical Statistics, Vol. 19, No. 3, 2002, pp. 235-249.
- I. Stancu and D. Rece, “The Relationship between Economic Growth and Money Laundering: A Linear Regression Model,” Theoretical and Applied Economics, Vol. 9, No. 9, 2009, pp. 3-8. http://www.doaj.org/doaj?func=abstract&id=452320
- K. M. Ramachandran and C. P. Tsoksos, “Mathematical Statistics with Applications,” Academic Press, London, 2009.
- Bank of Albania, “Eksport of Goods According to Partners,” Bank of Albania, Republic of Albania, 2011.
- Bank of Albania, “Governments Expenditures,” Bank of Albania, Republic of Albania, 2011.
- Bank of Albania, “Imports of Goods According to Partners,” Bank of Albania, Republic of Albania, 2011.
- General Directorate for the Prevention of Money Laundering, “Albanian Financial Intelligence Unit (AFIU),” Shtepiabotuese “Botart”, Republic of Albania, 2011.
NOTES
*There is an indecisive relationship between money laundering and GDP growth rate.
#Corresponding author.

