ABSTRACT

In this article, we use scaling function interpolation method to solve linear Fredholm integral equations, and we prove a convergence theorem for the solution of Fredholm integral equations. We present two examples which have better results than others.

1. Introduction

Integral equations play an important role in both mathematics and other applicable areas. Many physical phenomena can be modeled by differential equations. In fact, a differential equation can be replaced by an integral equation that incorporates its boundary conditions. Integral equations are also useful in many branches of pure mathematics as well. Here we study Fredholm integral equations [1-3].

Wavelets have been applied in a wide range of engineering and physicaldisciplines, and it is an exciting tool for mathematicians. In this paper we will find a numerical solution for the second kind Fredholm integral equation of the form

(1)

where the function 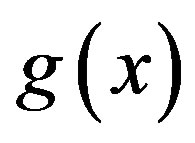and are 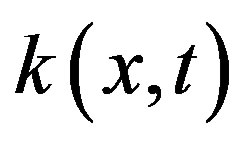given, and the unknown function 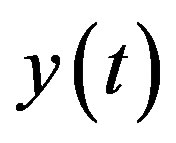is to be determined.

1.1. Wavelets

In this subsection we will provide a brief account of wavelet transform and Multiresolution analysis (MRA). We first define the scaling function 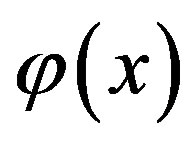and the sequence such that

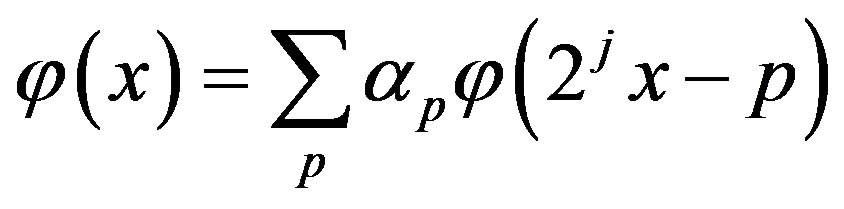(2)

By using this dilation and translation [4], we defined a nested sequence spaces 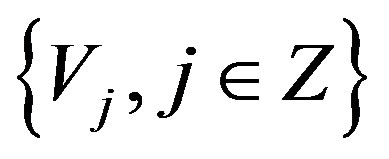which is called MRA of 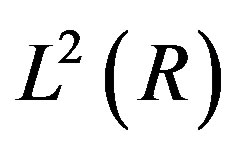with the following properties

(3)

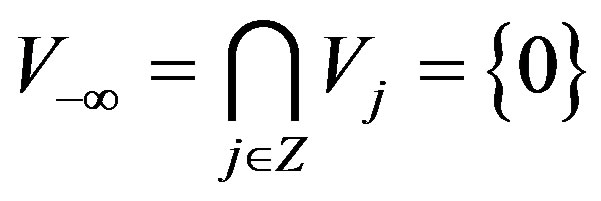(4)

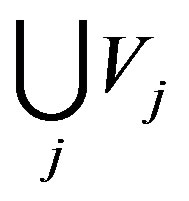is dense in

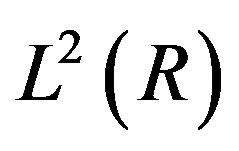(5)

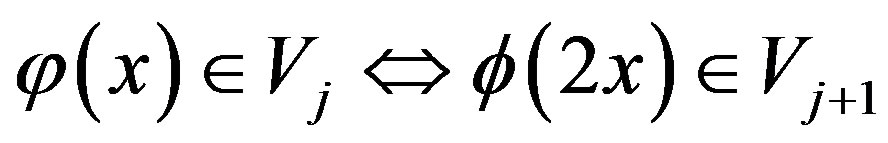(6)

For the subspace 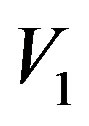is built by then 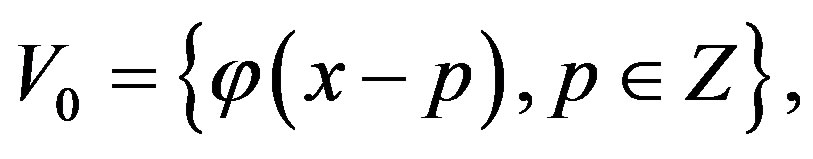and since 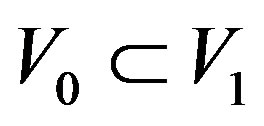we can write

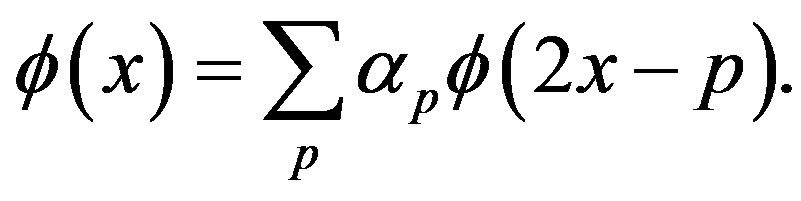
In general,

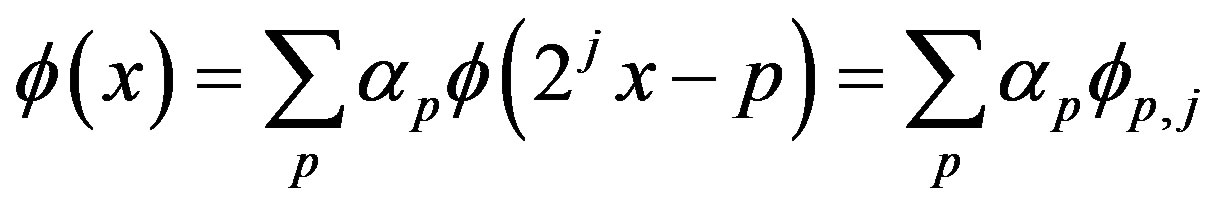
(7)

Any function 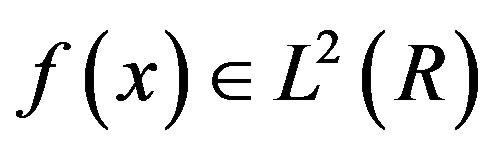can be approximated by scaling functions in one of the subspace in the given nested sequence. In fact, for each j we define the orthogonal complement subspace of 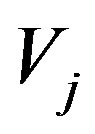in the subspace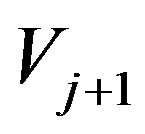. The orthogonal basis of 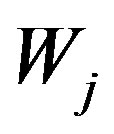is denoted by

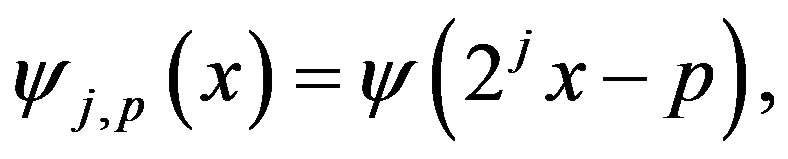(8)

and the wavelet function can be obtained by

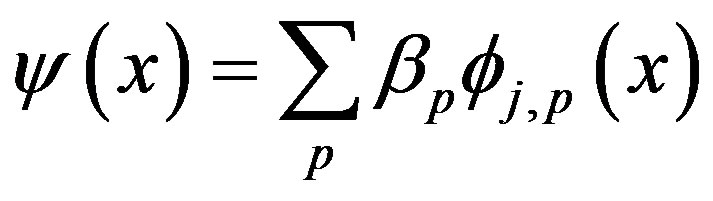. (9)

Some interesting properties of scaling and wavelet functions make wavelet method more efficiently than quadrature formula methods and spline approximations in solving Integral equations. A lot of computational time and storage capacity can be saved since we do not require a huge number of arithmetic operations partly due to the following properties.

1) Vanishing Moments:

(10)

and in this case the wavelet is said to have a vanishing moments of order m2) Semiorthogonality:

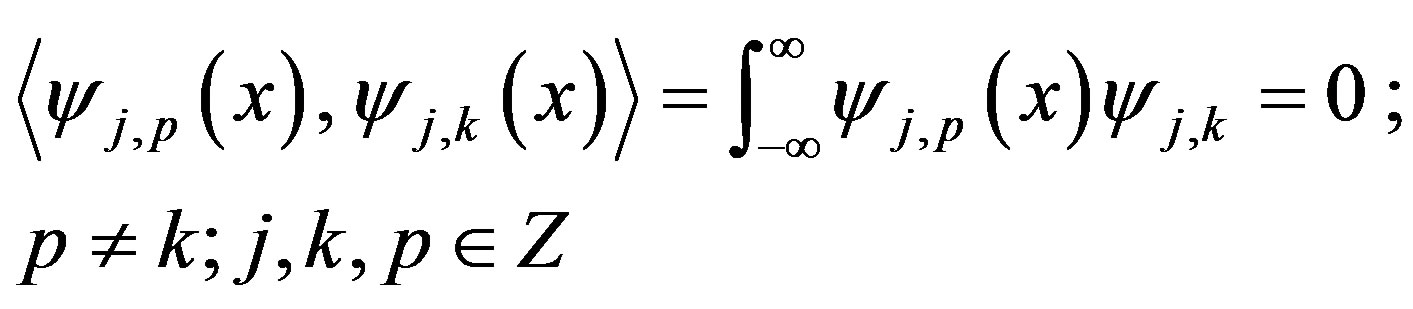(11)

The set of scaling functions are orthogonal at the same level n, which means:

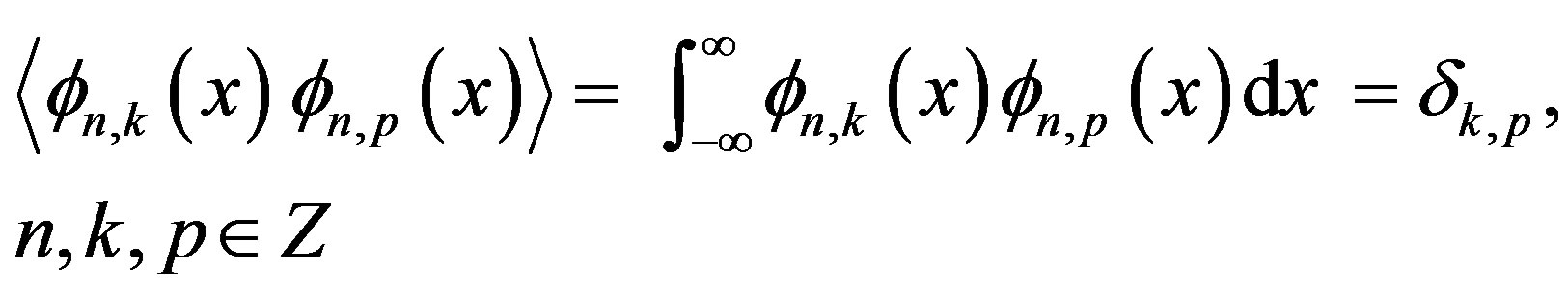(12)

Coiflet (of order L) has more symmetries and is an orthogonal multiresolution wavelet system with,

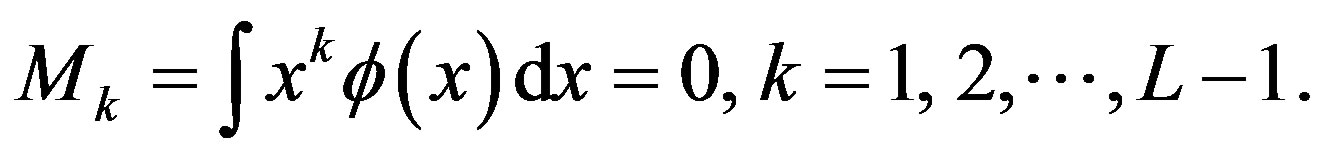(13)

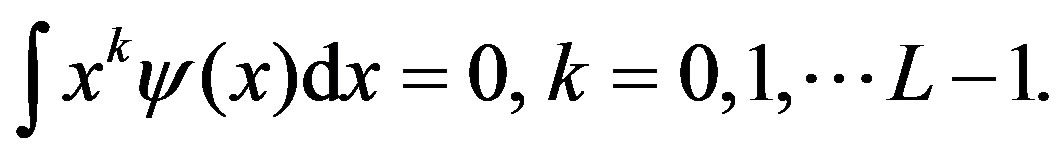(14)

where are the moments of the scaling functions.

1.2. Scaling Function Interpolation

The function 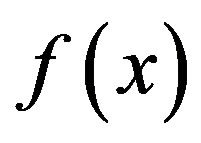can be interpolated by using the basis functions in the subspace 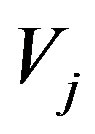as follows.

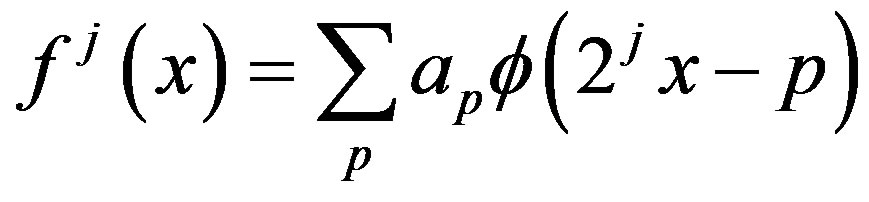(15)

where 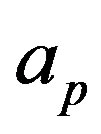are the coefficients evaluated by using equation (12) such that

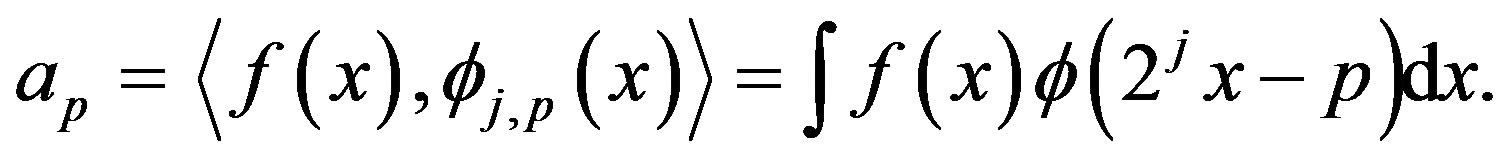(16)

Hence the equation (15) becomes:

.

On the other hand, one can use sampling values of 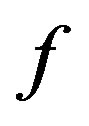at certain points to approximate the function 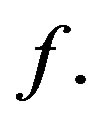It is proved in [5], namely, an interpolation theoremusing coiflet such that if 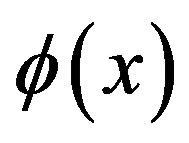and 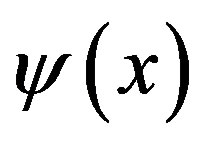are sufficiently smooth and satisfy the equations (10)-(14) and the function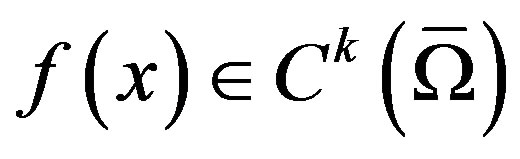, where is a bounded open set in

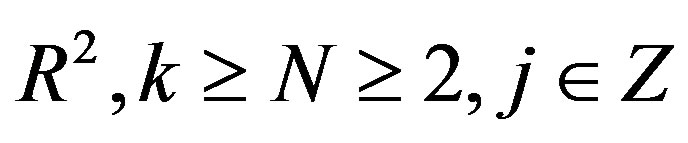
Then,

(17)

where the index set is

Sup denote the support of a function.

In addition, the moment 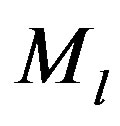satisfies

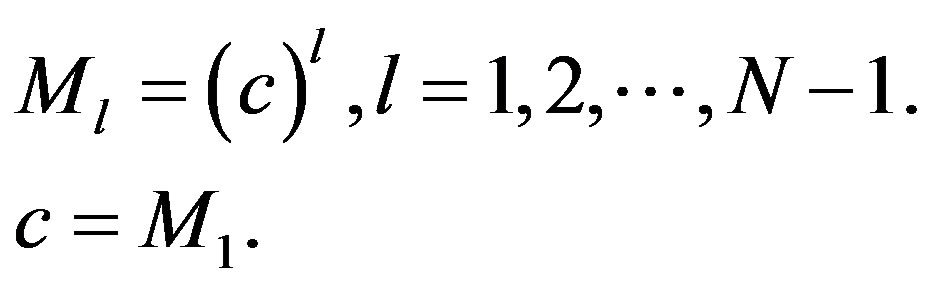
Then,

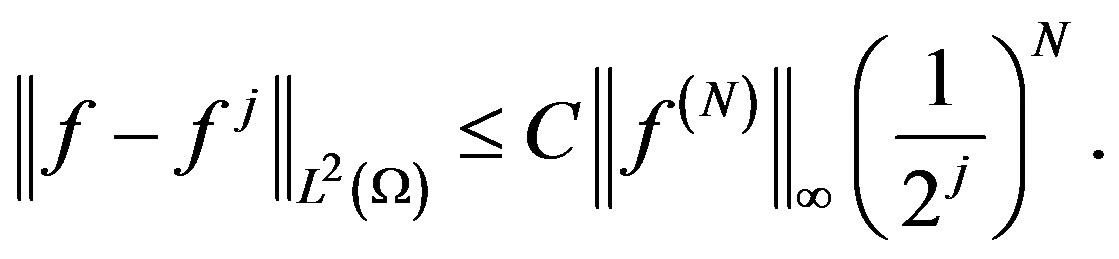
where is a constant depending only on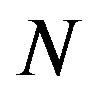, diameter of and

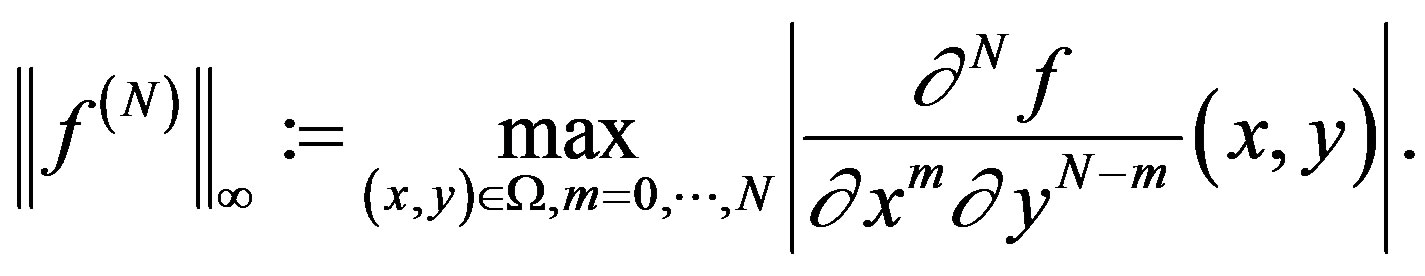
For the function with one variable, we have

(18)

and

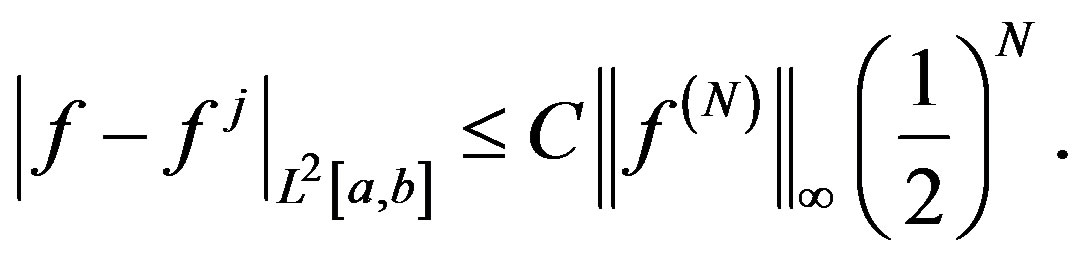(19)

where

(20)

2. Solve Fredholm Integral Equations Using Coiflet

In this section we will apply coiflet and the interpolation formula (18) to solve the Fredholm integral equation (1). The unknown function 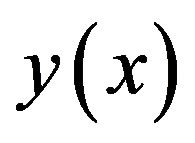in equation (1) can be expanded in term of the scaling functions 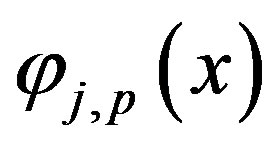in the subspace such that

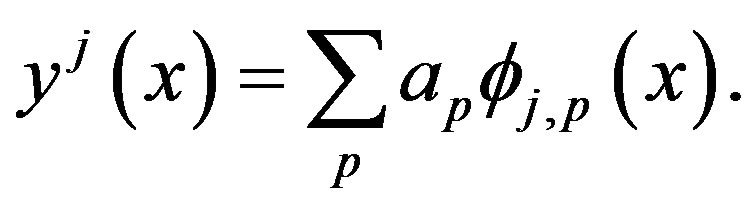(21)

Consider the equation (1) and the function 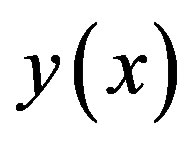which is defined on the interval [a, b] and the scaling function 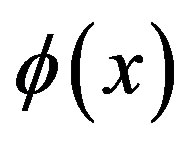defined on the interval 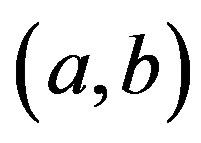then we have the index:

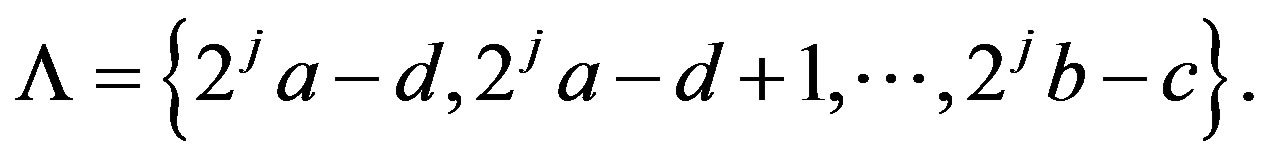
By applying equation (21) into equation (1), we get the system,

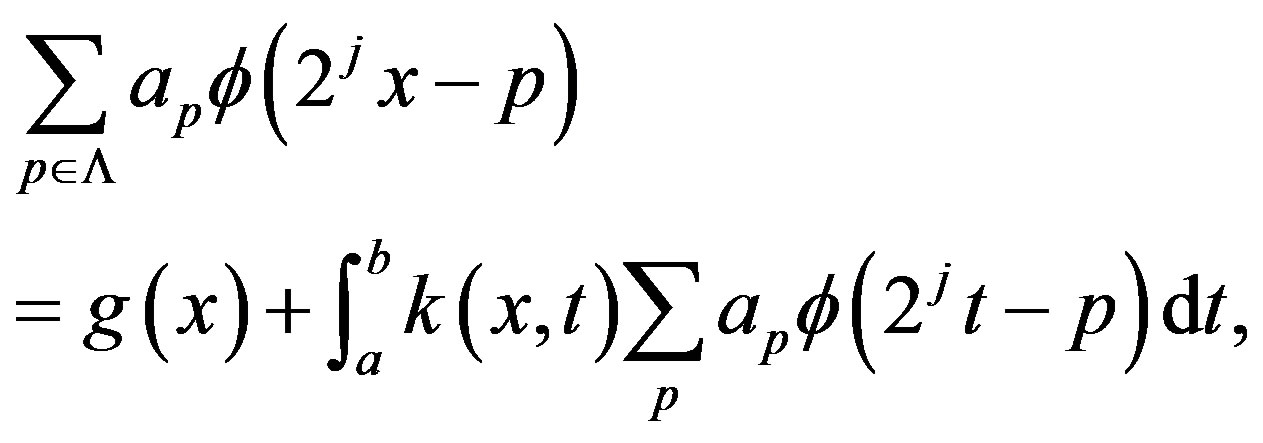(22)

which is equivalent to the following system,

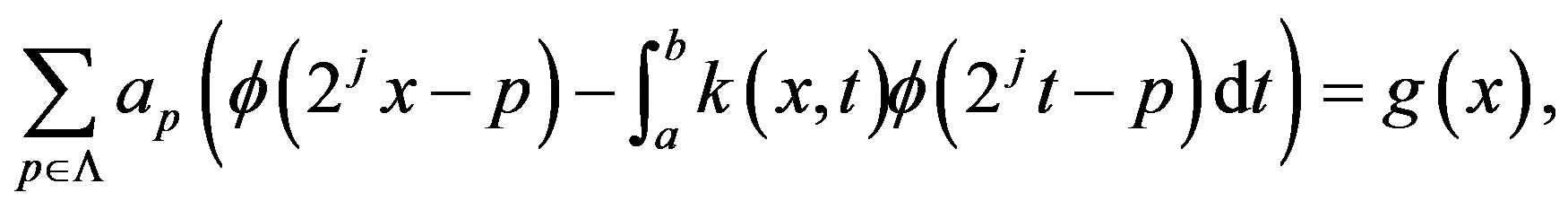(23)

where thecoefficients 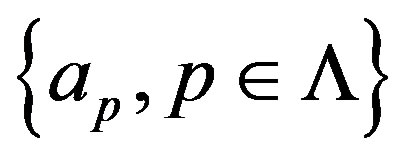can be evaluated by substituting 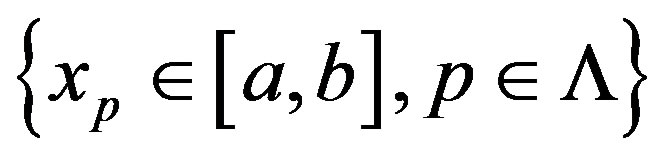into the system (23). Moreover, the system (23) can be expressed in compact form,

(24)

where

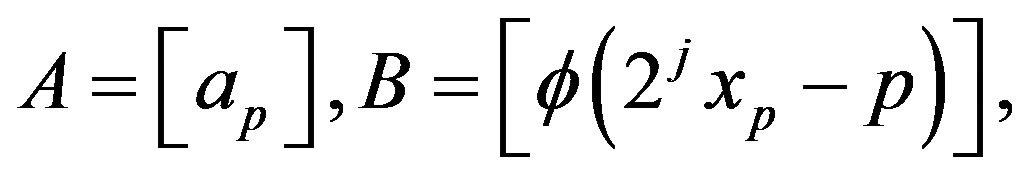
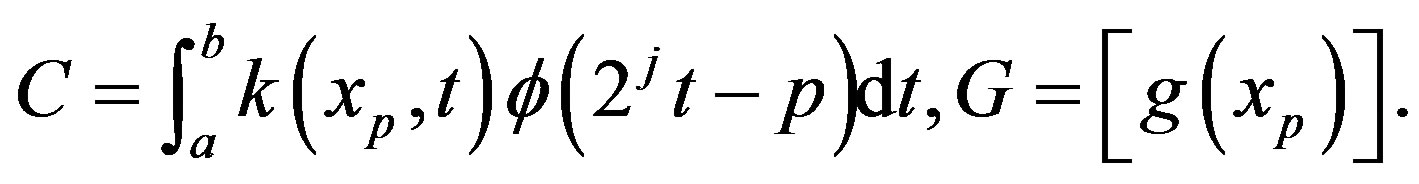
Then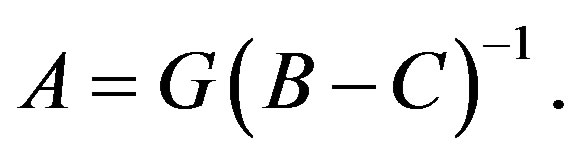

This gives rise to coefficients in (21) and we obtain a numerical solution of (1). In what follows, we will derive a convergence theorem of this numerical solution.

3. Error Analysis

In this section will discuss the convergence rate of our method for solving linear Fredholm integral equation (1).

Theorem 1. In equation (1), supposethat the function 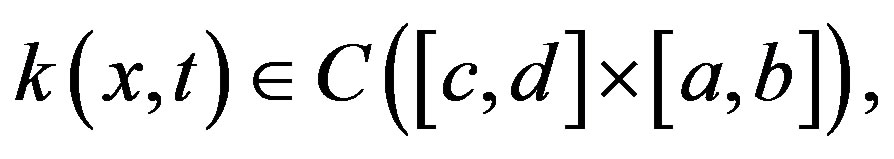and the functions 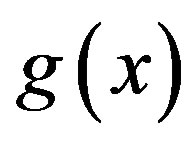and, for

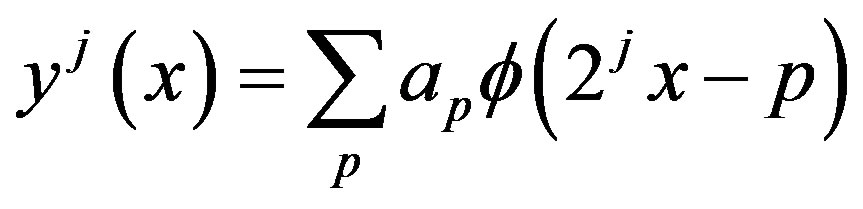(25)

is an approximate solution of the equation (1) with the coefficients obtained in (24). Then,

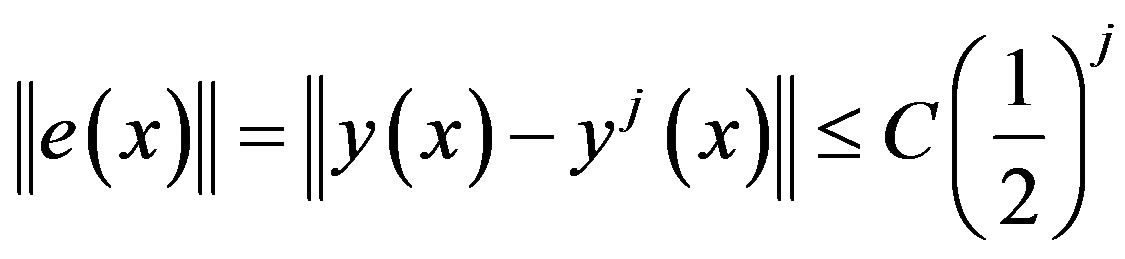(26)

where,

Proof. Subtracting equation (25) from equation (1) and taking the norm for both sides, we get the following

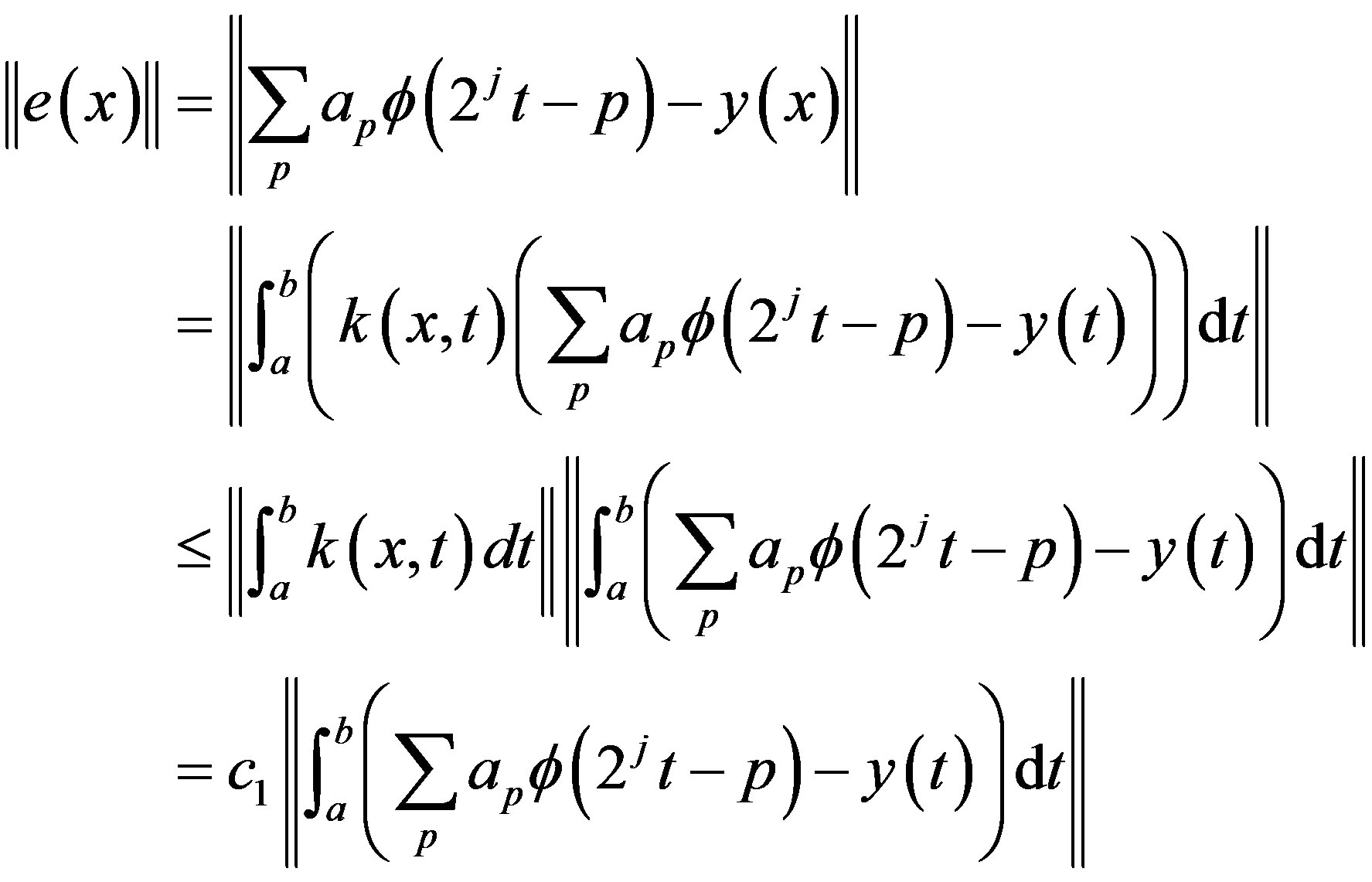(27)

where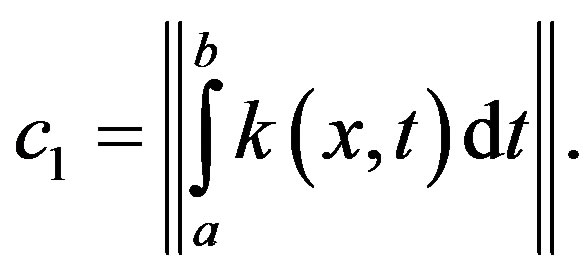

By [5], the unknown function can be interpolated by using coiflet such that:

(28)

Let 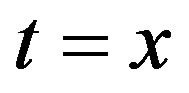in equation (28) then add and subtract it in equation (27), we get the following inequalities.

which equals to         the equation

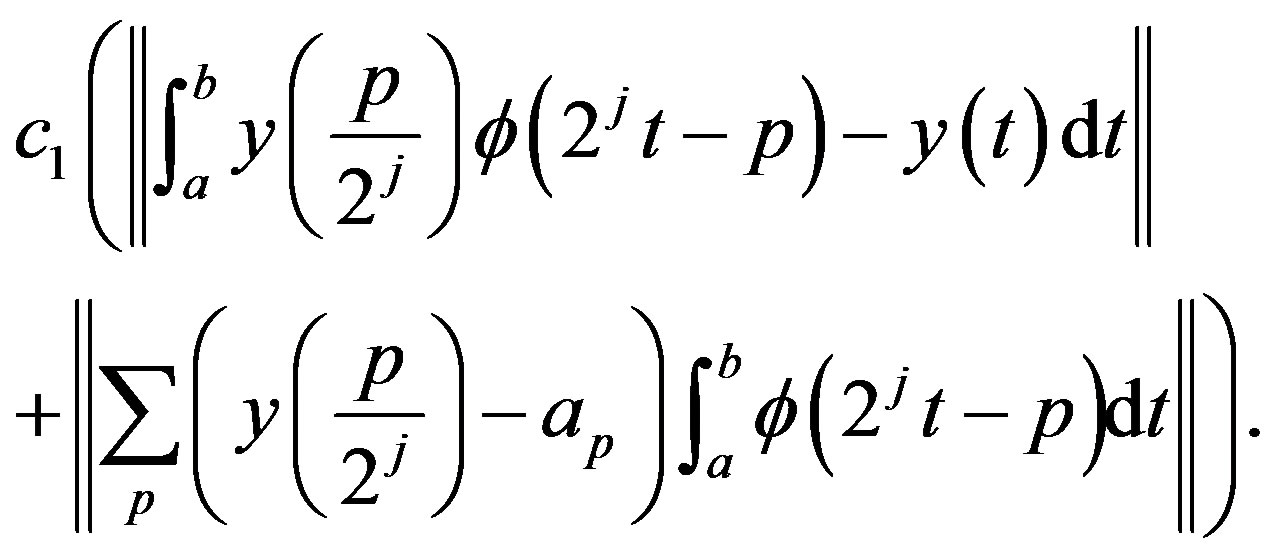(29)

By [5], we have

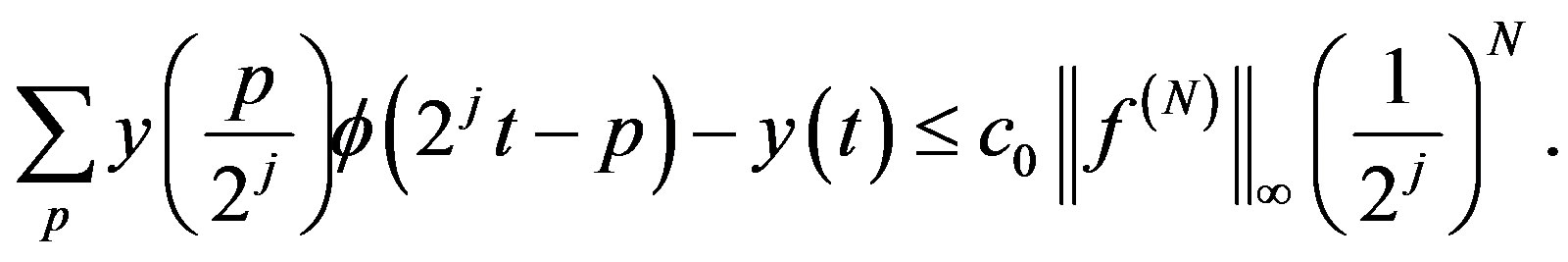(30)

Since is finite we define it as

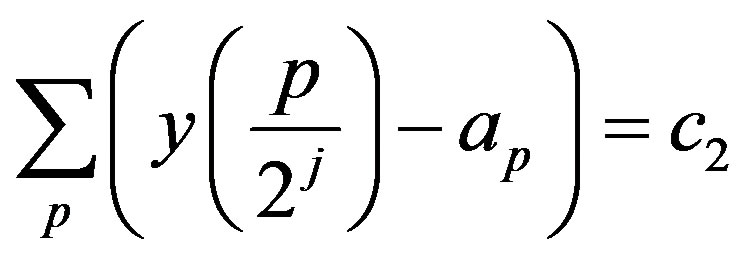. (31)

Using the above results and the orthonomality of the scaling functions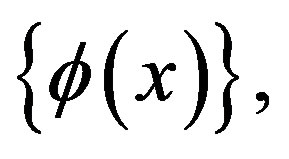, we conclude that

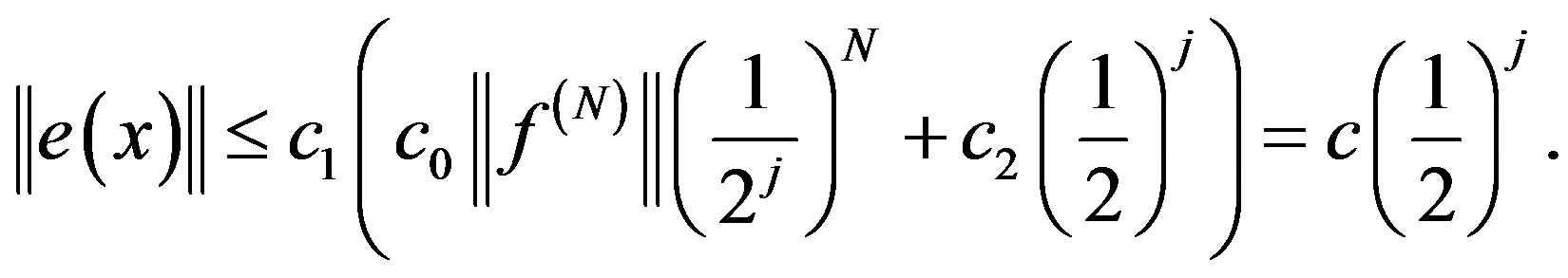(32)

4. Numerical Examples

In the following examples, we will solve linear Fredholm integral equation (1) using coiflet of order 5 and provide errors between exact solutions and our numerical solutions at different resolution levels. Both examples are also presented in [6] by using different method.

Example 1.

Consider 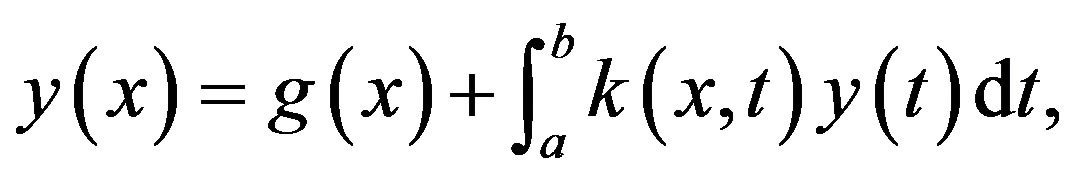where

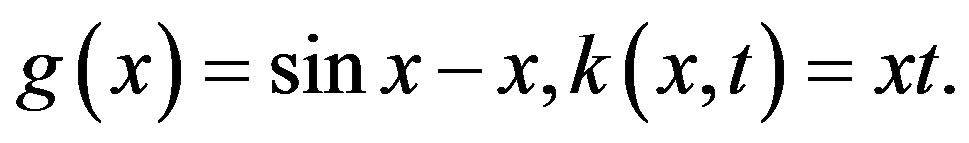
The exact solution is 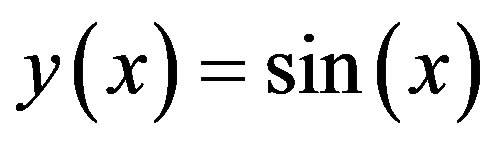and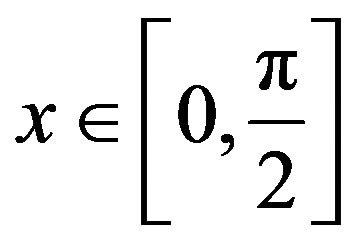

Example 2.

Consider

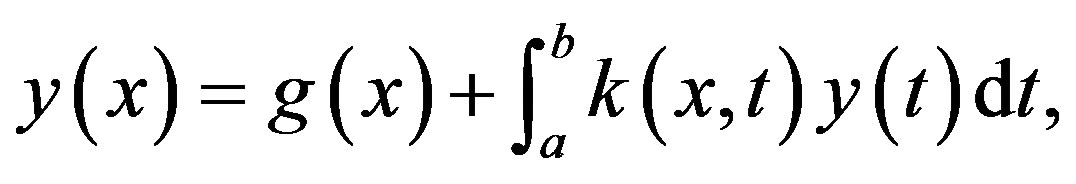
where 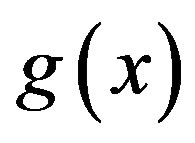and are given on the interval [0,1] such that,

The exact solution is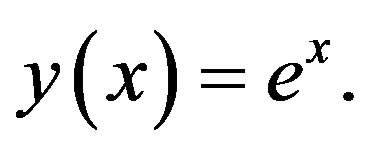

We use our interpolation method to solve the above integral equations, and find the errors in Table 1.

5. Conclusion

In this work, we use our interpolation method by using coiflets to solve Fredholm integral equations, and compare our results with those in [6]. It turns out our method is more efficient with better accuracy. Moreover, our method can be applied to different kind of integral equations as well as integral-algebraic equations. Although the results in the above examples don’t seem to have

correlation with the level of resolutions but they basically validate our theorem. In fact, we can also interpolate the given functions in the integral equation. This would simplify the calculations in finding numerical solutions of integral equations. It would be interesting to use our method to solve nonlinear integral equations as well.

6. Acknowledgements

The authors would like to thank the anonymous referees for their helpful comments.

REFERENCES